提出了一种新的聚类分析方法。 它的优点是计算复杂度较低。 该方法基于对有关单个坐标值的信息的一对对象属于同一类这一事实的投票计算。
引言
数据分析的巨大需求是开发有效的分类方法。 在这种方法中，仅基于有关单个指标值的信息，就需要将整个对象集划分为最佳类别数[Zagoruyko 1999]。
聚类分析是最流行的数据分析和数学统计方法之一。 聚类分析允许您仅使用有关对象的定量指标的信息（无需老师培训）即可自动查找对象的类别。 每个此类类别都可以通过其最具特色的对象之一来定义，例如，以指标为平均值。 有许多方法和方法可以对数据进行分类。
在聚类分析领域进行了现代研究，以改进确定复杂拓扑类别的方法[Furaoa 2007，Zagoruiko 2013]，并提高大数据情况下算法的速度。
在本文中，我们基于有关各个指标价值的信息，提出了一种基于获得同一类别中的一对对象的选票的分类方法。 建议考虑如果一对对象的各个指标的值在区间内且长度不超过给定值，则该对象属于同一类。
K均值法
k均值方法是最流行的聚类方法之一。 其目的是获得这样的数据中心，该数据中心对应于具有对称径向分布的数据类紧凑性的假设。 在给定编号\ textit {k}的情况下，确定此类中心位置的一种方法是EM方法。
在该方法中，顺序执行两个过程。
- 每个数据对象的定义 $ inline $ X_ {i} $ inline $ 最近的中心 $ inline $ C_ {j} $ inline $ ，并为此对象分配类标签 $ inline $ X_ {i} ^ {j} $ inline $ 。 此外，对于所有对象，确定它们属于不同类别。
- 计算所有类别中心的新位置。
从\ textit {k}类的中心的初始随机位置迭代地重复这两个过程，我们可以实现将对象分离为与类的径向紧缩性假设最接近的类。
一种新的作者分类算法将与k-means方法进行比较。
新方法
新的聚类分析算法是基于有关数据点各个坐标值的信息的属于不同聚类的投票而构建的。
- 指定值d ，该值表征两个对象被视为属于同一类的指示符间隔的长度。
- 所选指标 $内联$ x_ {i} $内联$ 并考虑所有成对的物体 $ inline $ \ left \ {O_ {l}，O_ {k} \ right \} $ inline $ 在哪里 $ inline $ l，k = 1 \ ldots N $ inline $ 。
- 如果 $ inline $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ right | \ le d $ inline $ 然后大小 $ inline $ r_ {lk}：= r_ {lk} + 1 $ inline $ （已添加语音）。
- 对所有指标重复执行动作2）和3） $ inline $ i = 1 \ ldots M $ inline $ 。
- 设置表征属于相同类别的最小投票数的值p 。
- 使用值对的键方法，确定所有类别的对象，以便在一个语音类别中，来自这些类别> = p的一对对象。
- 对d和p的所有值进行迭代，并重复项1）-6），以获得最接近给定类数g的类数。
为了将算法的复杂度降低至
N ，您可以为各个指标使用
T间隔，并用以下内容替换算法中的条款2）和3）：
1.选择了指标
$内联$ x_ {i} $内联$ 并考虑所有间隔
$ inline $ \ left [u_ {l}，w_ {l} \ right] $ inline $ 在哪里
$ inline $ l = 1 \ ldots T $ inline $ ：
$$显示$$ u_ {0} = \ min（x_ {i}）; u_ {0} = \ min（x_ {i}）; $$显示$$
$$显示$$ w_ {T} = \ max（x_ {i}）; $$显示$$
$$ display $$ s_ {i} = w_ {T} -u_ {0}； $$ display $$
$$ display $$ u_ {l} = u_ {0} + l \ cdot s_ {i}; $$ display $$
$$ display $$ w_ {l} = u_ {l} + d; $$ display $$
2.如果
$ inline $ x_ {i} ^ {k} \ in \ left [u_ {j}，w_ {j} \ right] $ inline $ 和
$ inline $ x_ {i} ^ {l} \ in \ left [u_ {j}，w_ {j} \ right] $ inline $ 在哪里
$内联$ j = 1 \ ldots T $内联$ 然后大小
$ inline $ r_ {lk}：= r_ {lk} + 1 $ inline $ （为语音添加第
i个指示符的唯一键
l ，
k ）。
数值实验
具有对人类直观的分类的数据被视为初始数据。
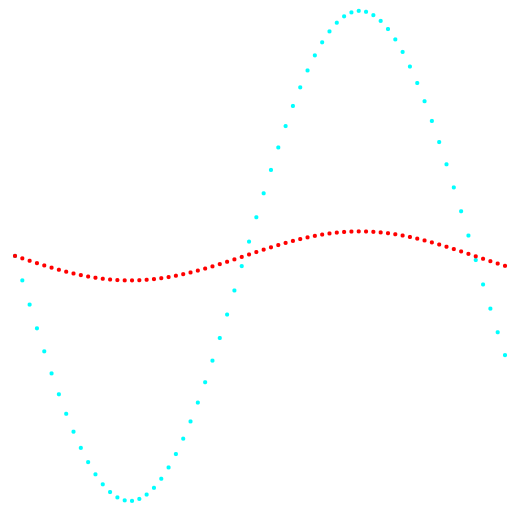
图1和2显示了k均值方法和新分类方法的分类结果。
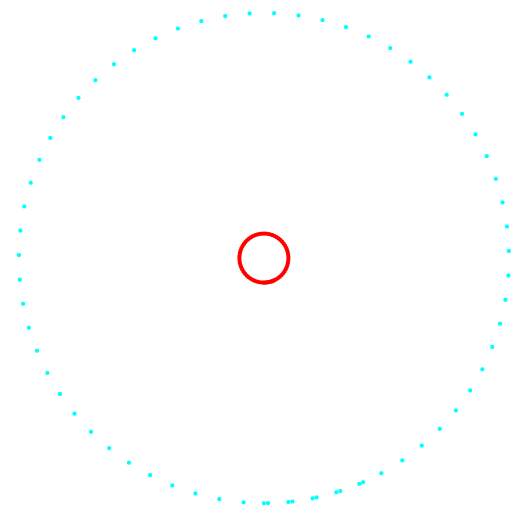图 1.投影1-2和数据分类。左边是k-means方法，右边是作者的方法。
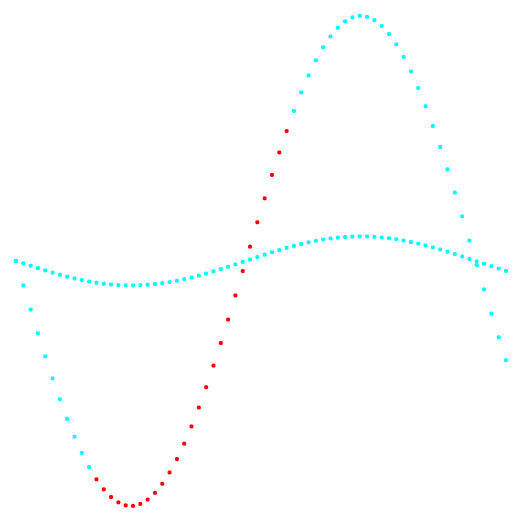
图 2.投影2-3和数据分类。左边是k-means方法，右边是作者的方法。
两种方法的比较结果表明，该方法在检测复杂拓扑集群方面具有明显的优势。
软件实施
k均值聚类方法以编程方式作为Web应用程序实现。 使用Zend框架将应用程序的计算部分提交给用PHP编写的服务器。 应用程序界面使用HTML，CSS，JavaScript，jQuery编写。 注册新用户后，可以从
http://svlaboratory.org/application/klaster2获得该应用程序。 该应用程序使您可以可视化对象在给定坐标平面中属于不同聚类的归属。
结论
提出了一种新的分类方法。 该方法的优点是可以识别复杂的拓扑，非径向分布的类，并且算法的复杂性和动作更少，这在大型数据阵列的情况下尤其有利。
参考文献- Zagoruyko N.G. 数据和知识分析的应用方法。 新西伯利亚：数学研究所出版社，1999.270页。
- Zagoruyko N.G.，Borisova I.A.，Kutnenko O.A.，Levanov D.A. 检测实验数据阵列中的模式//计算技术。 -2013.Vol.18.No.S1。 S.12-20。
- Shen Furaoa，Tomotaka Ogurab，Osamu Hasegawab一种增强的自组织增量神经网络，用于在线无监督学习。 长谷川实验室，2007。