翻译是为“ R上的应用分析”课程的学生准备的。
这是我第一次尝试基于真实数据对客户进行集群，这给了我宝贵的经验。 互联网上有很多关于使用数值变量进行聚类的文章，但是要找到分类数据的解决方案（要困难些）并不是那么简单。 分类数据的聚类方法仍在开发中，在另一篇文章中，我将尝试另一种。
另一方面，许多人认为聚类分类数据可能不会产生有意义的结果-这在一定程度上是正确的（请参阅
关于CrossValidated的
精彩讨论 ）。 有一次，我想到：“我在做什么？ 他们可以简单地分为同类。” 但是，也不总是建议使用队列分析，尤其是对于数量众多且级别较高的类别变量：您可以轻松处理5-7个队列，但如果您有22个变量，每个变量有5个级别（例如，具有离散估计1的客户调查， ，2、3、4和5），并且您需要了解要与哪些特征的客户群打交道-您将获得22x5的同类群组。 没有人愿意为这样的任务而烦恼。 在这里，群集可能会有所帮助。 因此，在这篇文章中，我将讨论我自己开始聚类后想知道的内容。
群集过程本身包括三个步骤：
- 建立异质矩阵无疑是聚类中最重要的决定。 所有后续步骤将基于您创建的相异矩阵。
- 聚类方法的选择。
- 聚类评估。
这篇文章将是一种介绍，描述群集的基本原理及其在环境R中的实现。
差异矩阵
聚类的基础将是差异矩阵，该矩阵用数学术语描述了数据集中的点彼此之间有多少不同。 它使您可以进一步将最接近的点组合在组中，或者将最远的点分开-这是聚类的主要思想。
在这一阶段，数据类型之间的差异非常重要，因为差异矩阵基于各个数据点之间的距离。 容易想象数字数据点之间的距离（一个著名的例子是
欧几里得距离 ），但是对于分类数据（R中的因子），一切并不是那么明显。
为了在这种情况下构造不相似矩阵，应使用所谓的Gover距离。 我不会深入研究这个概念的数学部分，我只会提供链接：
在这里和
那里 。 为此，我更喜欢将
daisy()与
cluster包中的
metric = c("gower")使用。
差异矩阵准备就绪。 对于200个观测值，它可以快速构建，但是如果您要处理大量数据集，则可能需要大量计算。
实际上，很有可能首先必须清理数据集，执行从行到因子的必要转换，并跟踪缺失值。 在我的情况下，数据集还包含缺少值的行，这些值每次都经过精美的聚类，因此在我查看这些值之前，这似乎是一种宝藏（阿拉斯！）。
聚类算法
您可能已经知道聚类是
k均值和分层的 。 在本文中，我将重点介绍第二种方法，因为它更灵活并且支持多种方法：您可以选择
聚集 （从下到上）或
分区 （从上到下）聚类算法。
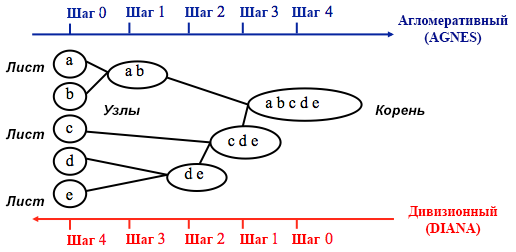资料来源：《 UC商业分析R编程指南》聚集聚类从
n个聚类开始，其中
n是观察值的数量：假定它们中的每一个都是一个单独的聚类。 然后，算法尝试在它们之间查找并分组最相似的数据点-这就是簇形成的开始方式。
分区聚类以相反的方式执行-最初假设我们拥有的所有n个数据点都是一个大群集，然后将最不相似的数据点划分为单独的组。
在决定选择这些方法中的哪种时，尝试所有选项总是有意义的，但是总的来说，
聚集聚类更适合识别小型聚类，并且大多数计算机程序都使用聚集聚类，而分区聚类更适合于识别大型聚类 。
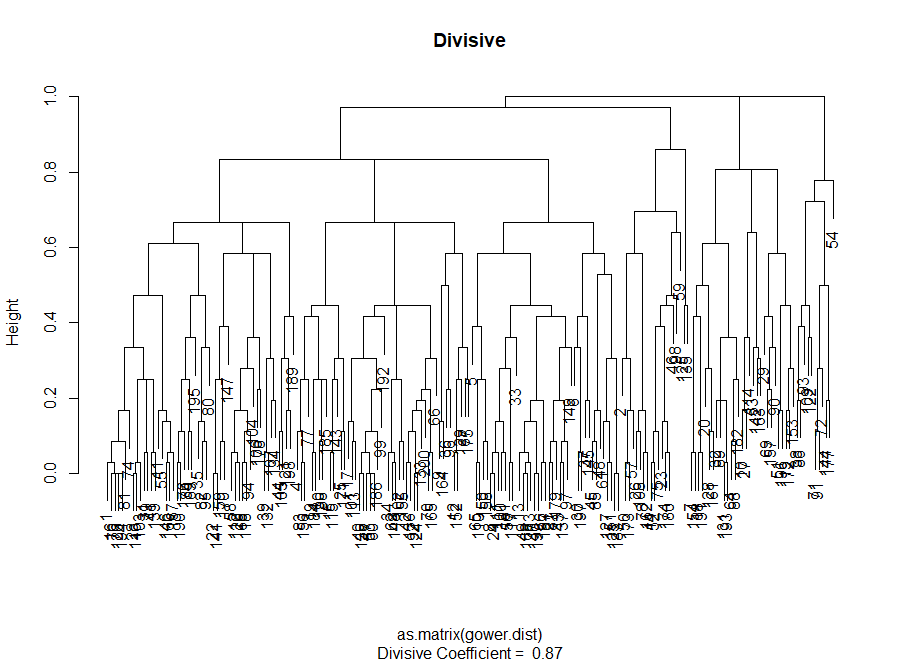
就个人而言，在决定使用哪种方法之前，我更喜欢看树状图-聚类的图形表示。 正如您稍后将看到的，有些树状图很平衡，而另一些则很混乱。
＃以下代码的主要输入是相异性（距离矩阵）
聚类质量评估
在这一阶段，有必要在不同的聚类算法和不同数量的聚类之间进行选择。 您可以使用不同的评估方法，不要忘了以
常识为指导。 我用粗体和斜体突出显示这些词，因为选择的意义
非常重要 -从实际的角度来看，簇的数量和将数据划分为组的方法应该是实用的。 分类变量的值组合的数量是有限的（因为它们是离散的），但是基于它们的任何细分都不是有意义的。 您可能也不想拥有很少的集群-在这种情况下，它们将被过于笼统。 最后，这完全取决于您的目标和分析任务。
通常，在创建集群时，您有兴趣获取明确定义的数据点组，以使集群内此类点之间的距离（
或紧度 ）最小，而组之间的距离（
可分离性 ）则最大。 这很容易直观地理解：点之间的距离是根据相异性矩阵获得的相异性的度量。 因此，聚类质量的评估是基于对紧密度和可分离性的评估。
接下来，我将演示两种方法，并说明其中一种可以给出毫无意义的结果。
- 弯头法 ：如果要进行分析的最重要因素是群集的紧凑性，即组内的相似性，则从此开始。
- 轮廓评估方法 ：用作数据一致性度量的轮廓图显示了一个群集中的每个点与相邻群集中的点的接近程度。
在实践中，这两种方法通常会产生不同的结果，这可能会引起一些混淆-使用不同数量的聚类将实现最大的紧凑性和最清晰的分离，因此常识和对数据真正含义的理解将起重要作用在做出最终决定时。
您还可以分析许多指标。 我将它们直接添加到代码中。
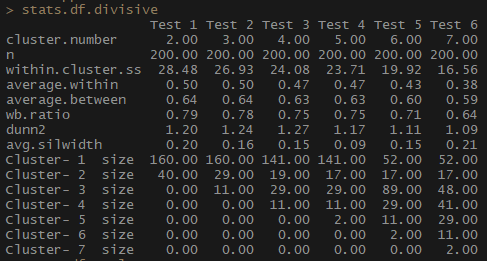
因此，表示簇内观测值之间的平均距离的“平均值”指标会降低，而“集群” ss（簇内观测值之间的距离的平方之和）也会减小。 轮廓的平均宽度（avg.silwidth）不会发生明显变化，但是仍然可以看到相反的关系。
请注意，群集大小不成比例。 我不会急于处理集群中无数的观测值。 原因之一是数据集可能不平衡，分析中的某些观察结果将超过所有其他观察结果-这不好，很可能会导致错误。
stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #stats.df.aggl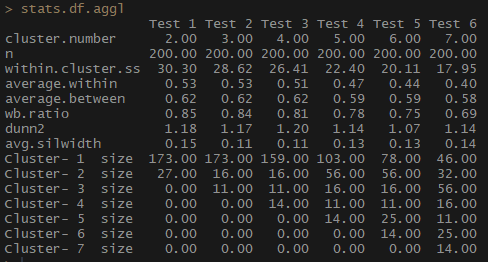
请注意，通过基于完全通信方法的聚集层次聚类，可以更好地平衡每个组的观察数量。
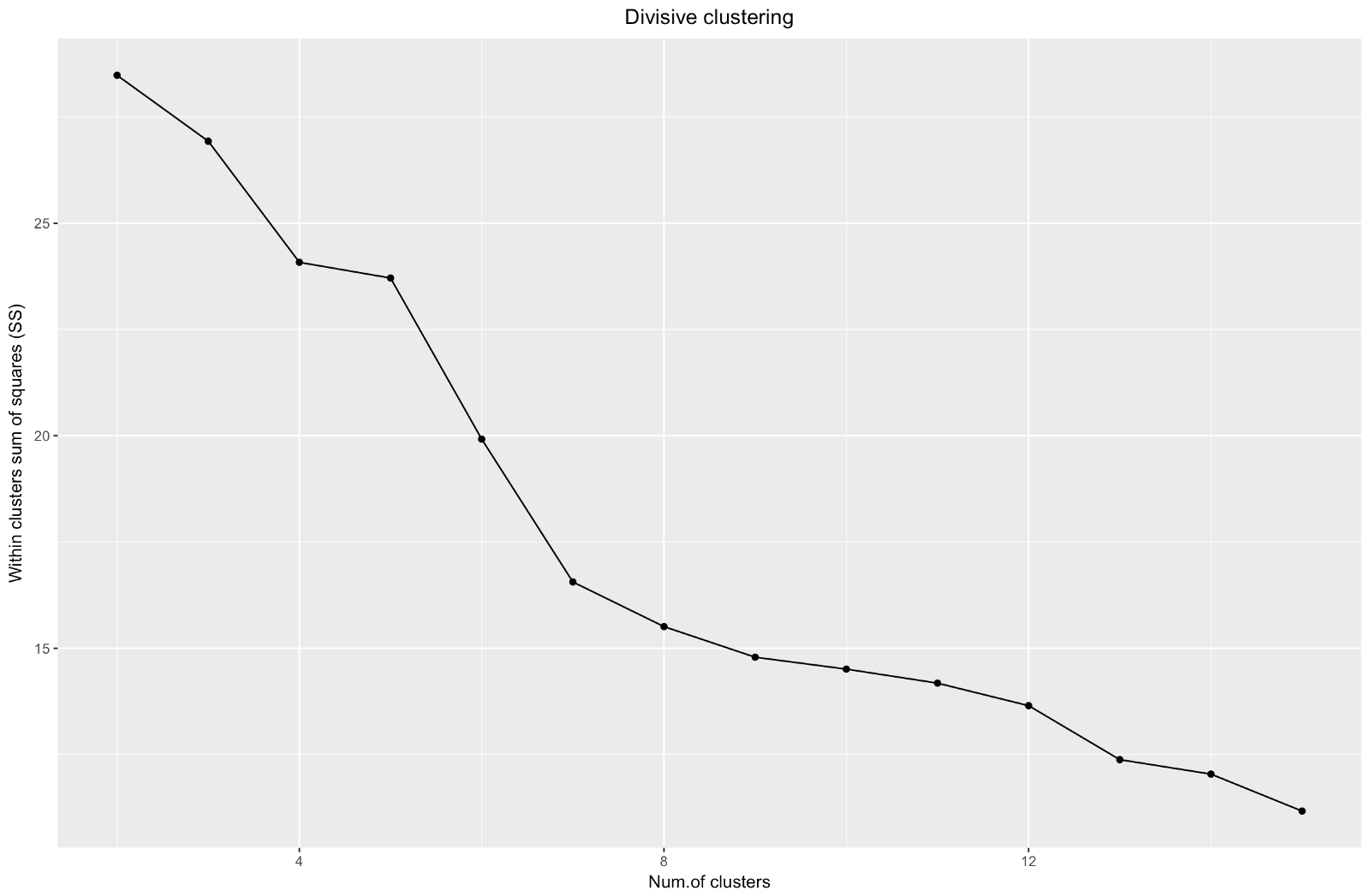
因此，我们创建了“肘”图。 它显示了观测值之间平方距离的总和（我们将其用作观测值接近程度的度量-值越小，集群内的度量彼此之间越接近）对于不同数量的集群而言如何变化。 理想情况下，我们应该在进一步的聚类仅使平方和（SS）略有减少的点上看到明显的“肘部弯曲”。 对于下图，我将在约7处停止。尽管在这种情况下，其中一个集群将仅包含两个观察值。 让我们看看在聚集集群期间会发生什么。
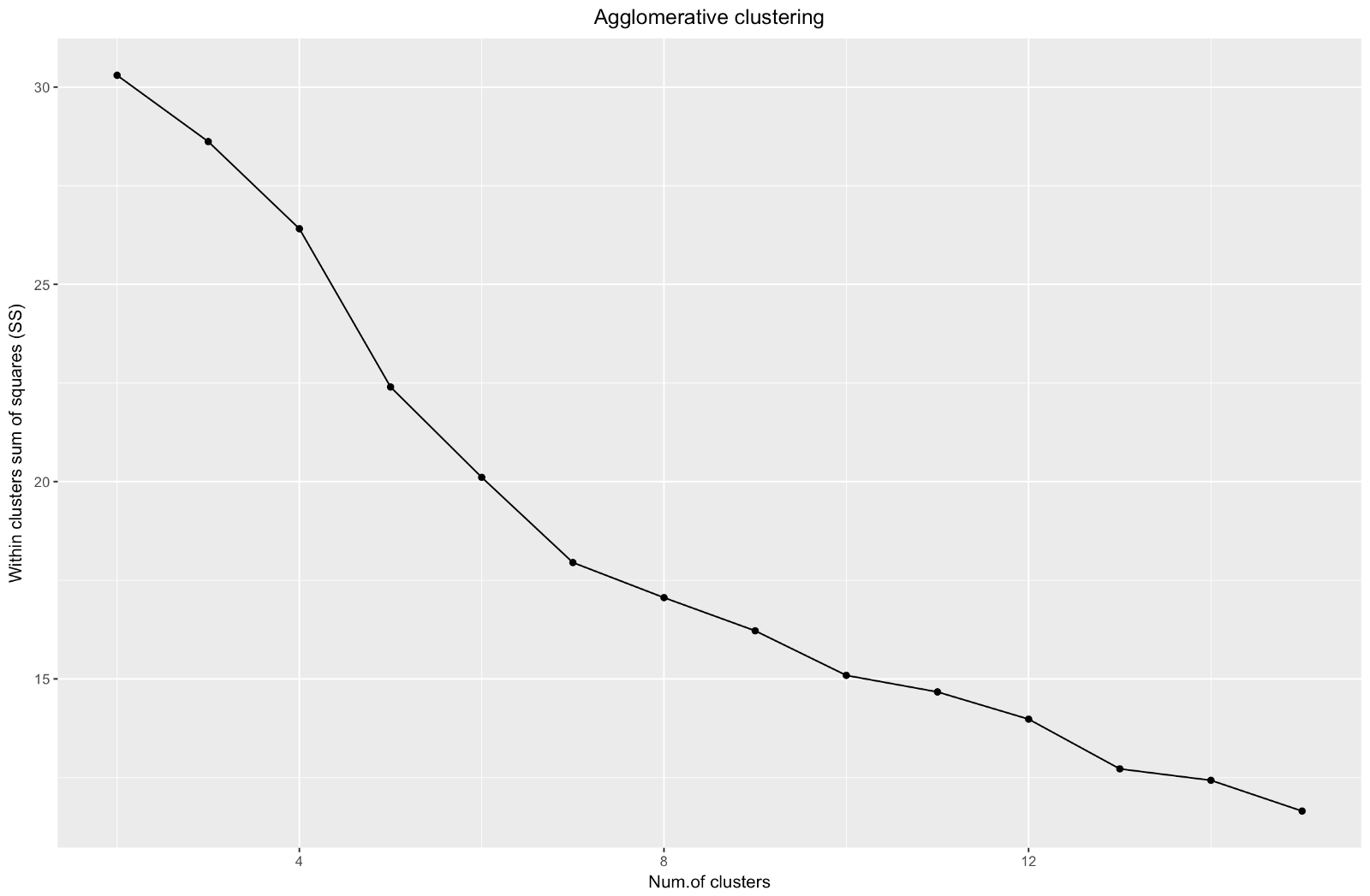
聚集的“弯头”类似于除法，但图形看起来更平滑-弯曲不太明显。 与分区聚类一样，我将重点关注7个聚类，但是，在这两种方法之间进行选择时，我更喜欢通过聚结方法获得的聚类大小-最好彼此具有可比性。
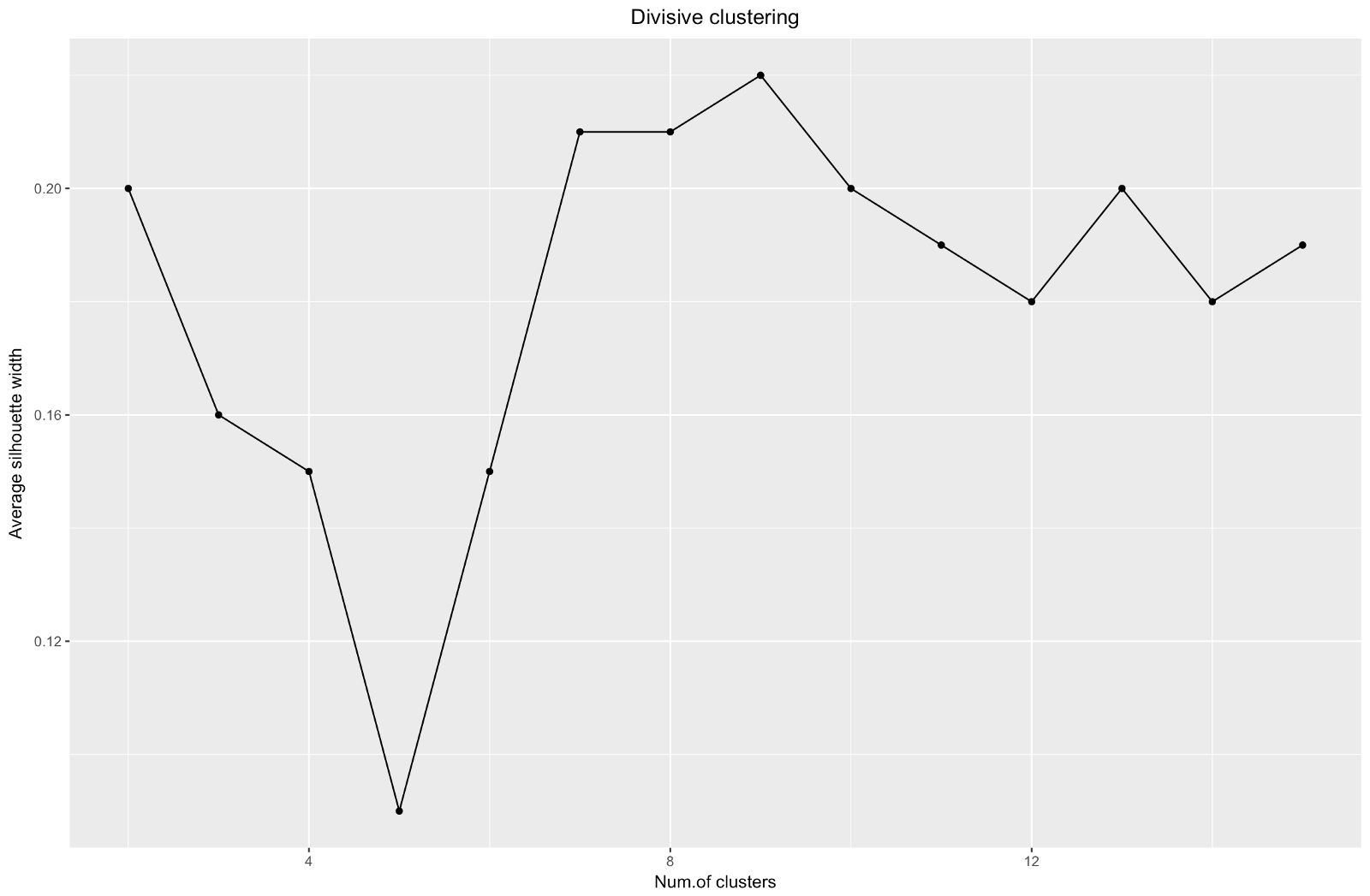
使用轮廓估计方法时，应该选择给出最大轮廓系数的量，因为您需要的簇之间的距离足够远，可以被认为是分开的。
轮廓系数的范围是–1到1，其中1表示群集中的一致性好，而–1不太好。
在上面的图表中，您将选择9个群集而不是5个群集。
为了进行比较：在“简单”情况下，轮廓图与下面的相似。 不太像我们的，但是差不多。
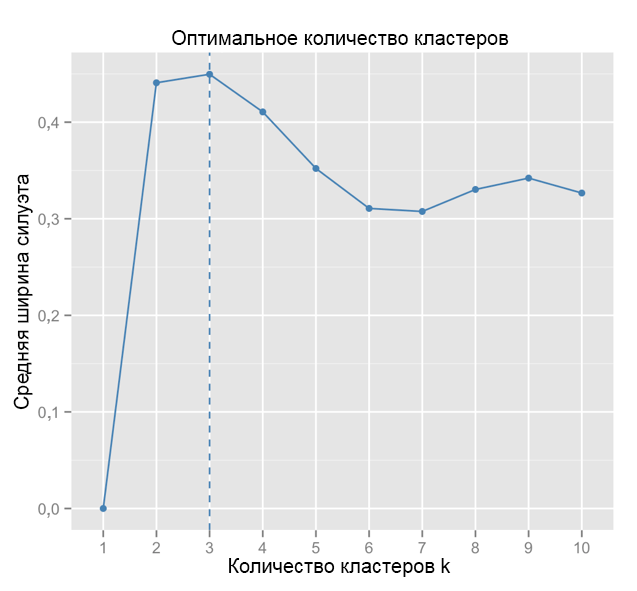资料来源： 数据水手 ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5))
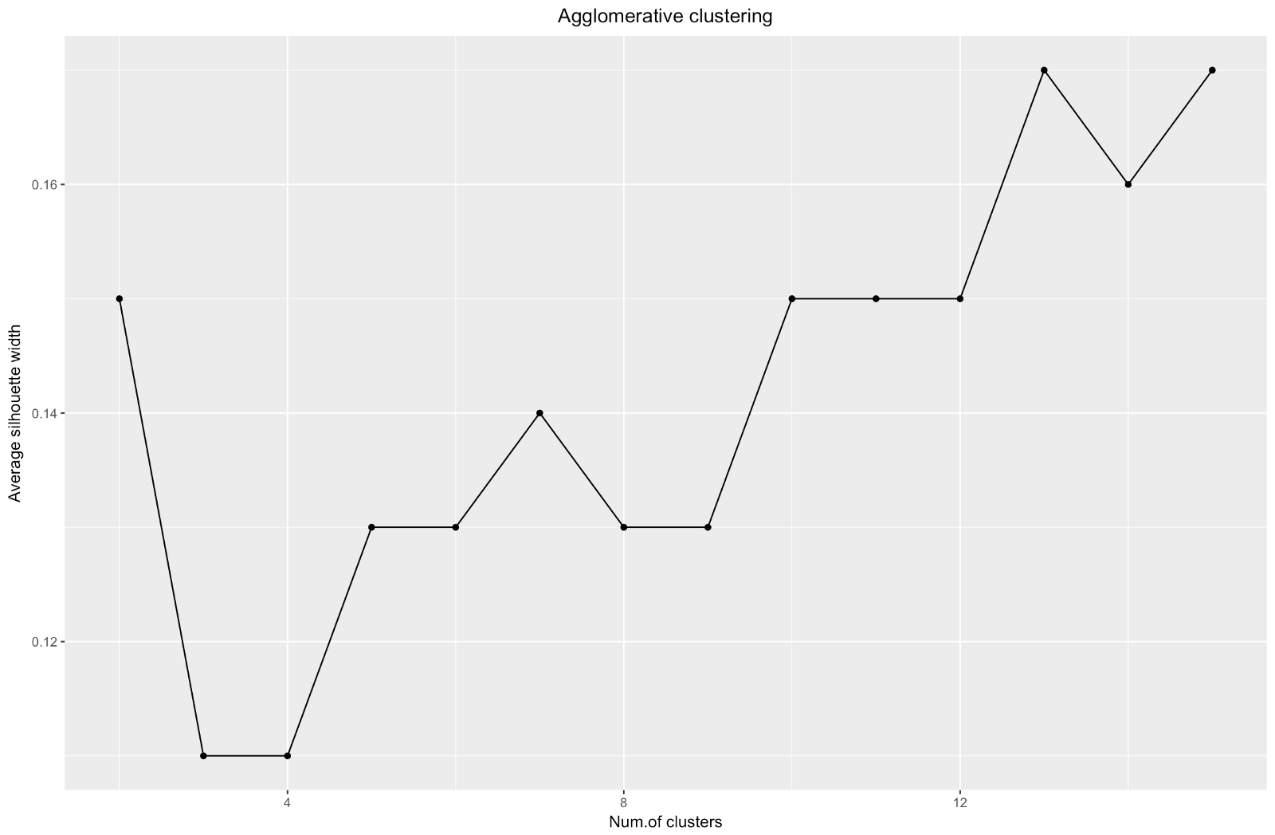
轮廓宽度图告诉我们：拆分数据集的次数越多，群集变得越清晰。 但是，最终您将达到各个要点，并且您不需要这样做。 但是，如果您开始增加簇
数k ，这正是您所看到的。 例如，对于
k=30我得到以下图形：
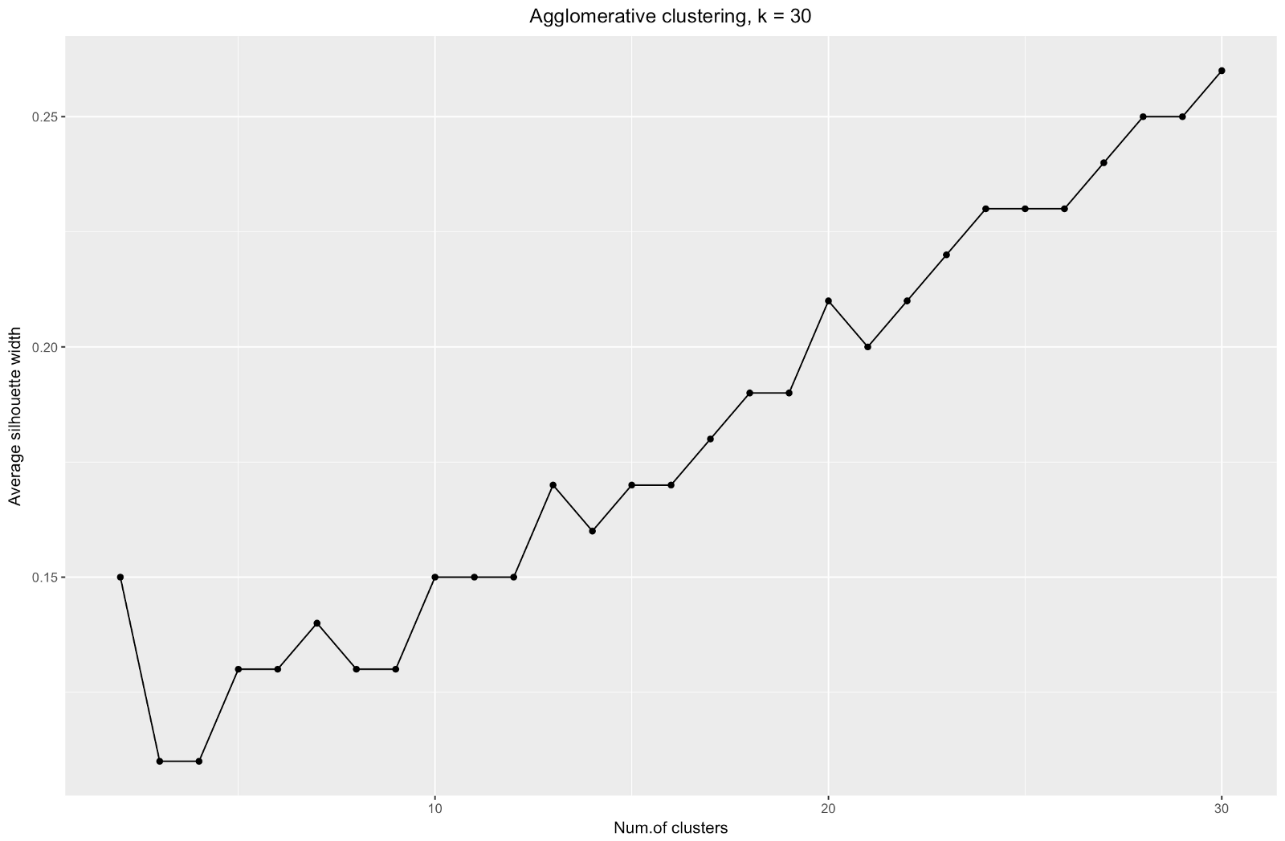
总结一下：分割数据集越多，聚类越好，但是我们无法达到单个点（例如，在上图中，我们选择了30个聚类，而我们只有200个数据点）。
因此，在我们看来，聚集聚类似乎更加平衡：聚类大小或多或少具有可比性（用除法划分时只看一个只有两个观察值的聚类！），我将停止使用此方法获得的7个聚类。 让我们看看它们的外观和组成。
数据集包含6个变量，需要以2D或3D形式显示，因此您必须努力工作！ 分类数据的性质也施加了一些限制，因此现成的解决方案可能不起作用。 我需要：a）观察如何将观察分为几类； b）了解观察如何进行分类。 因此，我创建了a）彩色树状图，b）每个聚类中每个变量的观察数的热图。
library("ggplot2") library("reshape2") library("purrr") library("dplyr")
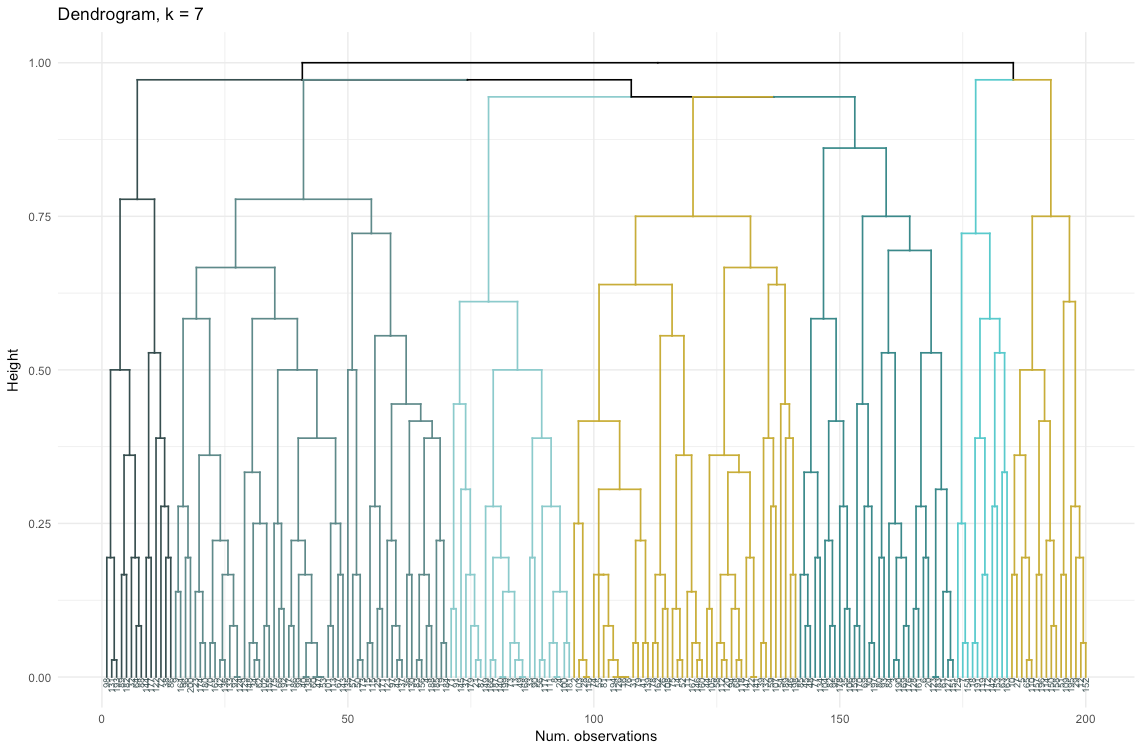
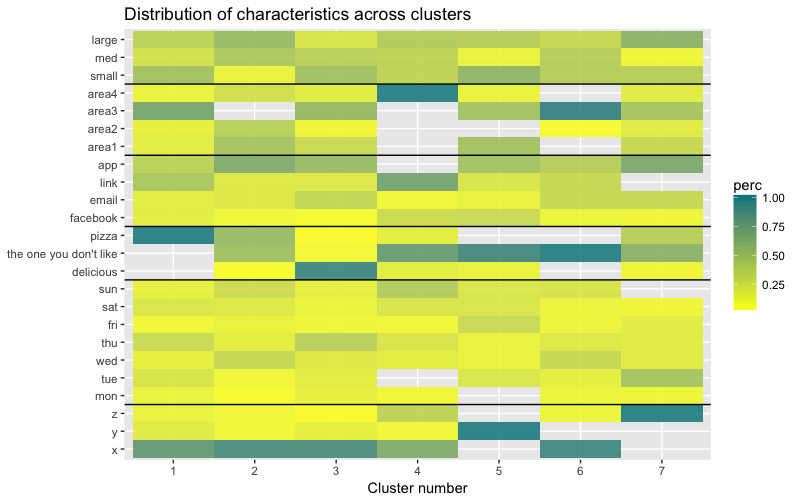
热图以图形方式显示在初始因子（我们开始使用的变量）的每个因子水平上进行了多少观察。 深蓝色对应于群集内相对大量的观测值。 此热图还显示，对于一周中的一天（星期日，星期六，星期一）和购物篮大小（大，中，小），每个单元中的客户数量几乎相同-这可能意味着这些类别对于分析不是决定性的，并且也许不需要考虑它们。
结论
在本文中，我们计算了相异矩阵，测试了聚类和分层聚类的方法，并熟悉了用于评估聚类质量的弯头和轮廓方法。
分区和聚集的层次聚类是研究该主题的一个很好的开始，但是如果您想真正掌握聚类分析，请不要停止在此。 还有许多其他方法和技术。 与聚类数值数据的主要区别是相异矩阵的计算。 在评估聚类的质量时，并非所有标准方法都能给出可靠且有意义的结果-轮廓法很可能不合适。
最后，由于自从创建此示例以来已经过去了一段时间，现在我发现我的方法存在许多缺陷，并且很高兴收到任何反馈。 我的分析中的一个重要问题与聚类无关，
我的数据集在许多方面
都不平衡 ，这一刻仍无法解决。 这对聚类产生了显着影响：70％的客户属于“公民身份”因素的一个级别，并且该组支配了大多数获得的聚类，因此很难计算该因素其他级别之间的差异。 下次，我将尝试平衡数据集并比较聚类结果。 但是在另一篇文章中有更多关于此的内容。
最后，如果您想克隆我的代码，以下是指向github的链接：
https :
//github.com/khunreus/cluster-categorical希望您喜欢这篇文章！
帮助我的资料来源：
分层集群指南（数据准备，集群，可视化）-对于R环境中的业务分析感兴趣的人，该博客将很有趣：
http ：
//uc-r.imtqy.com/hc_clustering和
https：// uc-r。 imtqy.com/kmeans_clustering群集验证：
http :
//www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/( k-):
https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/denextend, :
https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function, :
https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/:
https://jcoliver.imtqy.com/learn-r/008-ggplot-dendrograms-and-heatmaps.html,
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ ( GitHub:
https://github.com/khunreus/EnsCat ).