神经网络和深度学习，第5章：为什么深度神经网络如此难训练？

假设您是一名工程师，并且要求您从头开始开发计算机。 一旦坐在办公室，您就在设计逻辑电路，分配“与”或“或”阀等方面费劲–突然间您的老板进来告诉您一个坏消息。 客户只是决定对项目添加一个意外的要求：整个计算机的方案不应超过两层：



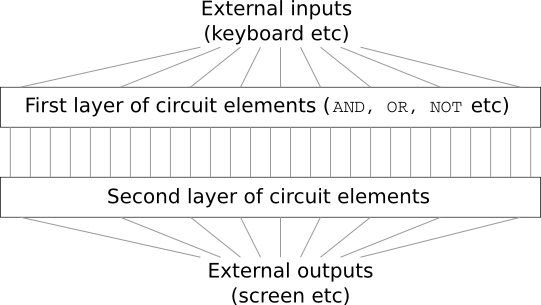
您会惊讶地告诉老板：“是的，客户疯了！”

老板回答：“我也这么认为。 但是客户必须得到他想要的。”

实际上，从狭义上讲，客户并不完全是疯子。 假设您被允许使用特殊的逻辑门，该逻辑门允许您通过AND连接任意数量的输入。 并且您可以将NAND门与任意数量的输入一起使用，即，这种门通过AND叠加很多输入，然后反转结果。 事实证明，使用这种特殊的阀门，您仅需两层回路即可计算任何功能。

但是，仅仅因为可以做某件事并不意味着它值得做。 在实践中，当解决与逻辑电路设计相关的问题（以及几乎所有算法问题）时，我们通常从解决子问题开始，然后逐步组装完整的解决方案。 换句话说，我们通过许多抽象层次来构建解决方案。

例如，假设我们设计了一个将两个数字相乘的逻辑电路。 我们可能希望从实现诸如加两个数字之类的操作的子电路中构建它。 反过来，附加子电路将由两个位相加的子电路组成。 粗略地说，我们的方案如下所示：



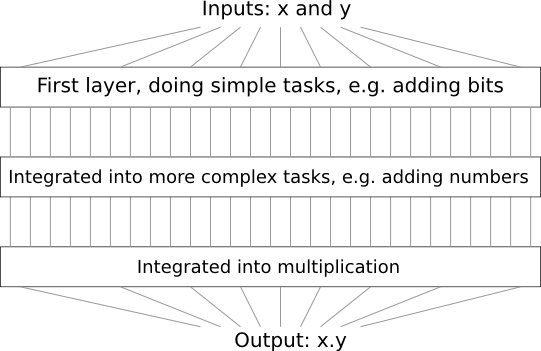
即，最后的电路包含至少三层电路元件。 实际上，当我们将子任务分解为比我描述的子任务更小的子任务时，它可能会超过三层。 但是您了解了原理。

因此，深层方案可简化设计过程。 但是它们不仅在设计上有帮助。 有数学证据表明，要在非常浅的电路中计算某些函数，就需要使用比深度电路大得多的元素数量。 例如，1980年代有一系列著名的科学著作 ，其中表明，计算一组位的奇偶性需要使用浅电路的门数量成倍增加。 另一方面，当使用深度方案时，使用小型方案更容易计算奇偶校验：您只需计算位对的奇偶校验，然后使用结果来计算位对的奇偶校验，依此类推，从而快速达到通用奇偶校验。 因此，深层方案可能比浅层方案更强大。

到目前为止，这本书已经使用了一种神经网络（NS）的方法，类似于疯狂客户的要求。 我们合作的几乎所有网络都有一个神经元的隐藏层（加上输入和输出层）：



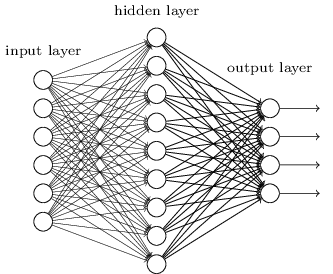
这些简单的网络非常有用：在前面的章节中，我们使用这种网络对手写数字进行分类，其准确性超过98％！ 但是，从直观上看，具有许多隐藏层的网络将更加强大：



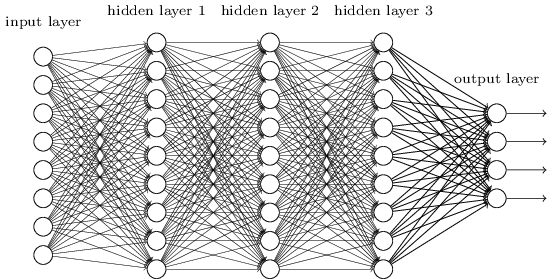
这样的网络可以使用中间层来创建许多抽象级别，就像我们的布尔方案一样。 例如，在模式识别的情况下，第一层的神经元可以学习识别面部，第二层的神经元可以识别更复杂的形状，例如从面部创建的三角形或矩形。 然后，第三层将能够识别甚至更复杂的形状。 依此类推。 在解决识别复杂模式的问题时，这些许多抽象层可能会给深层网络一个令人信服的优势。 此外，与电路情况一样， 有理论结果证实，深层网络固有地比浅层网络具有更多的功能。

我们如何训练这些深度神经网络（GNS）？ 在本章中，我们将尝试使用训练算法中的主力训练STS-随机梯度后向传播下降。 但是，我们会遇到一个问题-我们的STS不会比浅表的STS更好（如果完全超过）。

根据上面的讨论，这种失败似乎很奇怪。 但是，我们不会放弃STS，而是会更深入地研究问题，并尝试理解STS为何难以训练。 当我们仔细研究这个问题时，我们会发现STS中的不同层以不同的速度学习。 特别是，如果对网络的最后一层进行了良好的培训，则第一层经常会在培训期间卡住，几乎一无所获。 这不仅是运气不好。 我们将发现与基于梯度的学习技术的使用相关的学习速度下降的根本原因。

深入研究这个问题，我们发现相反的现象也可能发生：早期的层可以很好地学习，而后面的层则可以被卡住。 实际上，我们将发现深层多层NS中与梯度下降训练相关的内部不稳定性。 并且由于这种不稳定，早期或晚期都经常卡在训练中。

所有这些听起来都很不愉快。 但是陷入这些困难之后，我们可以开始就有效培训STS所需要做的事情提出想法。 因此，这些研究将为下一章的良好准备，在下一章中，我们将使用深度学习来解决图像识别问题。

渐变梯度问题

那么，当我们尝试训练深度网络时出了什么问题？

为了回答这个问题，我们返回到仅包含一个隐藏层的网络。 和往常一样，我们将MNIST数字分类问题用作学习和实验的沙盒。

如果要在计算机上重复所有这些步骤，则必须安装Python 2.7，Numpy库以及可从存储库中获取的代码副本：

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

您只需下载数据和代码即可无需git。 转到src子目录，然后从python shell加载MNIST数据：

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

配置网络：

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

这样的网络在输入层中具有784个神经元，对应于输入图像的28×28 = 784像素。 我们使用30个隐藏的神经元和10个周末，对应于MNIST的十个可能的分类选项（“ 0”，“ 1”，“ 2”，...，“ 9”）。

让我们尝试使用一次包含10个训练示例的微型包，一次学习30个完整纪元来训练我们的网络，学习速度η= 0.1，正则化参数λ= 5.0。 在训练期间，我们将通过validation_data跟踪分类的准确性：

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

我们得到的分类精度为96.48％（或如此-数字会因不同的发射而有所不同），与我们之前采用类似设置的结果相当。

让我们添加另一个也包含30个神经元的隐藏层，并尝试使用相同的超参数训练网络：

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

分类准确度提高到96.90％。 它令人鼓舞-深度略有增加会有所帮助。 让我们添加30个神经元的另一个隐藏层：

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

它没有帮助。 结果甚至下降到96.57％，接近原始浅层网络的值。 如果我们添加另一个隐藏层：

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

然后，分类精度将再次下降到96.53％。 从统计上讲，这种下降可能微不足道，但是没有什么好处。

这种行为似乎很奇怪。 从直觉上看，其他隐藏层应有助于网络学习更复杂的分类功能，并更好地应对任务。 当然，结果不应恶化，因为在最坏的情况下，附加层根本无法做任何事情。 但是，这不会发生。

那到底是怎么回事？ 让我们假设其他隐藏层原则上可以提供帮助，并且问题在于我们的训练算法没有找到正确的权重和偏移值。 我们想了解我们的算法有什么问题，以及如何对其进行改进。

要了解出了什么问题，让我们将网络学习过程可视化。 在下面，我构建了网络的一部分[784,30,30,10]，其中有两个隐藏层，每个层都有30个隐藏神经元。 在该图中，每个神经元都有一个指示条，指示学习网络过程中的变化速率。 一根大条表示神经元的重量和位移快速变化，而一根细条则意味着它们的变化缓慢。 更精确地，该条表示神经元的∂C/∂b梯度，即相对于位移的成本变化率。 在第二章中，我们看到该梯度值不仅控制训练过程中位移的变化率，而且还控制输入神经元权重的变化率。 如果您不记得这些细节，请不要担心：您只需要记住，这些指示条指示在训练网络期间神经元的权重和位移发生变化的速度。

为了简化该图，我仅在两个隐藏层中绘制了六个上部神经元。 我降低了传入神经元，因为它们没有权重或偏见。 我也省略了输出神经元，因为我们正在比较两层，因此比较具有相同数量神经元的层是有意义的。 该图是在培训的开始即使用网络初始化后立即使用generate_gradient.py程序构建的。



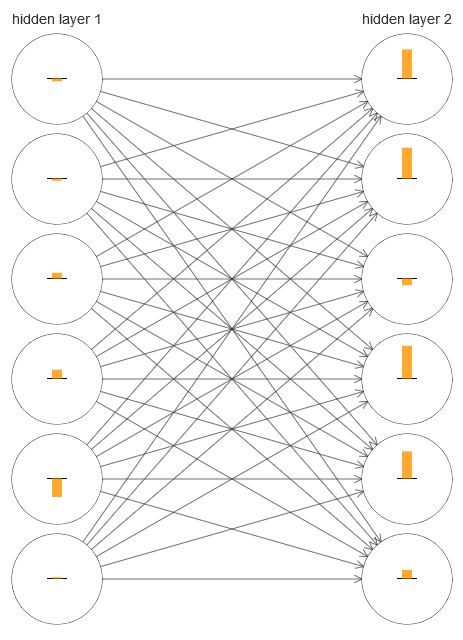
网络是偶然地初始化的，因此神经元训练速度的这种多样性不足为奇。 但是，立即引起注意的是，在第二个隐藏层中，这些条带基本上比第一层中的要多。 结果，第二层中的神经元将比第一层中的学习更快。 这是巧合，还是第二层的神经元通常比第一层的神经元学习更快？

确切地说，最好有一种比较第一隐藏层和第二隐藏层的学习速度的一般方法。 为此，让我们将梯度表示为δl _j =∂C/∂bl _j ，即，表示为^l号层中j号神经元的梯度。 在第二章中，我们将其称为“错误”，但在这里我将非正式地称为“梯度”。 非正式地-由于此值未明确包含按重量计算的成本的偏导数∂C/∂w。 可以将梯度δ1视为向量，其元素确定第一隐藏层的学习速度，而将δ2视为向量，其元素确定第二隐藏层的学习速度。 我们将这些向量的长度用作各层学习速度的近似估计。 例如，长度|| δ1 || 测量第一隐藏层的学习速度，长度|| δ2 || 测量第二个隐藏层的学习速度。

使用上述定义和相同的配置，我们发现|| δ1 || = 0.07，并且|| δ2 || = 0.31。 这证实了我们的怀疑：第二个隐藏层中的神经元比第一个隐藏层中的神经元学习得快得多。

如果我们添加更多隐藏层会怎样？ 在网络[784,30,30,30,10]中具有三个隐藏层的情况下，相应的学习速度将为0.012、0.060和0.283。 同样，第一个隐藏层的学习速度比最后一个要慢。 添加另一个包含30个神经元的隐藏层。 在这种情况下，相应的学习速度将为0.003、0.017、0.070和0.285。 模式被保留：早期的层比后面的层学习得慢。

我们从一开始就研究了学习速度-网络初始化之后。 学习时，速度如何变化？ 让我们回头看一下具有两个隐藏层的网络。 学习速度的变化如下：



为了获得这些结果，我使用了具有1000个训练图像和500个时代的训练的批量梯度下降。 这与我们通常的步骤略有不同-我没有使用迷你包装，只拍摄了1000张训练图像，而不是全套50,000张。 我并不想欺骗您，但事实证明，将随机梯度下降与微型数据包一起使用会给结果带来更多噪声（但如果将噪声平均，结果将是相似的）。 使用我选择的参数，可以很容易地平滑结果，以便我们可以看到发生了什么。

在任何情况下，如我们所见，两层以两种非常不同的速度（我们已经知道）开始训练。 然后，两层的速度都很快下降，然后反弹。 但是，一直以来，第一个隐藏层的学习速度都比第二个要慢。

那更复杂的网络呢？ 这是一个类似实验的结果，但是该网络具有三个隐藏层[784,30,30,30,10]：



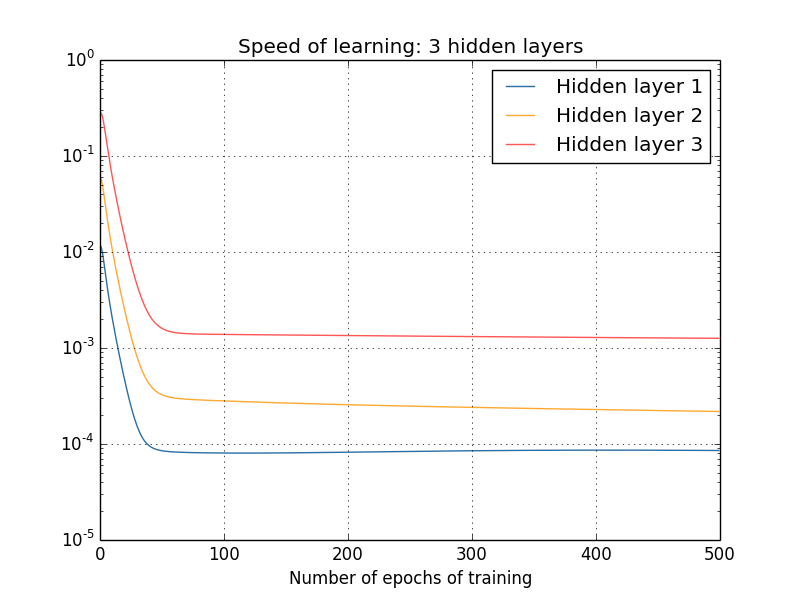
同样，第一个隐藏层的学习速度比最后一个要慢。 最后，让我们尝试添加第四个隐藏层（网络[784,30,30,30,30,10]），并查看训练后会发生什么：



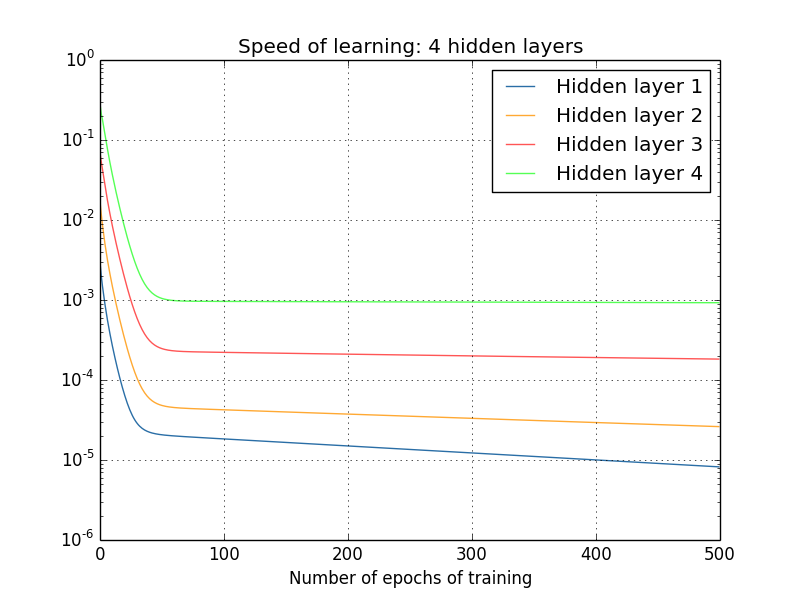
同样，第一个隐藏层的学习速度比最后一个要慢。 在这种情况下，第一个隐藏层的学习速度比最后一个隐藏层慢100倍。 难怪我们在学习这些网络时遇到这样的问题！

我们做了一个重要的观察：至少在某些GNS中，当沿隐藏层向相反方向移动时，梯度会减小。 也就是说，第一层的神经元比最后一层的神经元训练得慢得多。 尽管我们仅在一个网络中观察到了这种影响，但是在许多NS中发生这种情况有一些根本原因。 这种现象被称为“消失梯度问题”（参见工作1，2 ）。

为什么存在渐变衰落问题？ 有什么办法可以避免呢？ 培训STS时如何处理？ 实际上，我们很快就会发现这并不是不可避免的，尽管这种选择对她来说似乎并不很吸引人：有时在第一层中，梯度要大得多！ 这已经是梯度爆炸性增长的问题，它的好处不在于梯度消失的问题。 通常，事实证明，STS中的梯度是不稳定的，并且在第一层中易于爆炸性增长或消失。 这种不稳定性是梯度GNS训练的基本问题。 这是我们需要了解的，并可能以某种方式解决。

对渐变（或不稳定）渐变的反应之一是考虑这是否实际上是一个严重的问题？ 让我们简要地从NS转移注意力，并想象我们正在尝试从一个变量的数值上最小化函数f（x）。 如果导数f′（x）小，那不是很好吗？ 这是否意味着我们已经接近极端了？ 并且以同样的方式，GNS的第一层中的较小坡度是否表示我们不再需要大幅调整权重和位移？

当然不是 回想一下，我们随机初始化了网络的权重和偏移。 我们原始的权重和混合值不可能很好地满足我们从网络中获得的需求。 作为一个具体示例，请考虑网络中的第一层权重[784,30,30,30,10]，它对数字MNIST进行了分类。 随机初始化意味着第一层弹出有关传入图像的大多数信息。 即使对后面的层进行了仔细的训练，也仅由于缺乏信息，他们就很难确定传入的消息。 因此，绝对不可能想象第一层根本不需要培训。 如果要训练STS，我们需要了解如何解决梯度消失的问题。

是什么导致衰落梯度问题？ GNS中不稳定的渐变

要了解梯度消失的问题是如何出现的，请考虑最简单的NS：每层中只有一个神经元。 这是一个具有三个隐藏层的网络：



w ₁ ，w ₂ ，...是权重，b ₁ ，b ₂ ，...是位移，C是某个成本函数。 提醒一下，我会说神经编号j的输出a _j等于σ（z _j ），其中σ是通常的S型激活函数，而z _j = w _j a _{j − 1} + b _j是神经元的加权输入。 我在最后描述了成本函数，以强调成本是网络输出的函数，以及₄ ：如果实际输出接近您想要的输出，则成本将很小，而如果远，则成本将很大。

我们研究与第一个隐藏神经元相关的梯度∂C/∂b1。 我们找到∂C/∂b1的表达式，并且通过研究它，我们将理解为什么会出现消失梯度的问题。

我们首先说明∂C/∂b1的表达式。 它看起来固若金汤，但实际上它的结构很简单，我将尽快对其进行描述。 这是这个表达式（现在，忽略网络本身，并注意σ只是函数σ的派生）：



表达式的结构如下：对于网络中的每个神经元，都有一个乘法项σ'（z _j ），对于每个权重都有w _j ，并且还有最后一项costC /∂a4，与成本函数相对应。 请注意，我将相应的成员放在网络的相应部分之上。 因此，网络本身就是表达的记忆规则。

您可以将这种表达基于信念，而将其讨论直接跳到解释它与衰落梯度问题如何相关的地方。 这没有错，因为该表达式是我们对反向传播的讨论中的一个特例。 但是，很容易解释他的忠诚度，因此对您进行研究很有趣（也许很有启发性）。

想象一下，我们对偏移b ₁做了很小的Δb1改变。 这将在网络的其余部分发送一系列级联的更改。 首先，这将导致第一隐藏神经元Δa1的输出发生变化。 反过来，这迫使Δz2改变了第二隐藏神经元的加权输入。 然后，第二个隐藏神经元的输出中的Δa2将发生变化。 依此类推，直到输出值的ΔC变化为止。 事实证明：

$$

$$\ frac {\部分C} {\部分b_1} \大约\ frac {\ Delta C} {\ Delta b_1} \标签{114}$$

这表明我们可以导出梯度∂C/∂b1的表达式，仔细监视此级联中每个步骤的影响。

为此，让我们考虑Δb1如何导致第一个隐藏神经元的输出a ₁发生变化。 我们有一个₁ =σ（z ₁ ）=σ（w ₁ a ₀ + b ₁ ），因此

$$

$$\ Delta a_1 \大约\ frac {\部分\ sigma（w_1 a_0 + b_1）} {\部分b_1} \ Delta b_1 \标签{115}$$

$$

$$= \ sigma'（z_1）\ Delta b_1 \标签{116}$$

术语σ'（z ₁ ）应该看起来很熟悉：这是我们的表达式∂C/∂b1的_第一项 。 直观地，它将偏移量Δb1的变化变为输出激活的变化量Δa1。 Δa1的变化又引起第二个隐藏神经元的加权输入z ₂ = w ₂ a ₁ + b _2的变化 ：

$$

$$\ Delta z_2 \大约\ frac {\部分z_2} {\部分a_1} \ Delta a_1 \标签{117}$$

$$

$$= w_2 \ Delta a_1 \标记{118}$$

结合Δz2和Δa1的表达式，我们看到偏差b ₁的变化如何沿网络传播并影响z ₂ ：

$$

$$\ Delta z_2 \大约\ sigma'（z_1）w_2 \ Delta b_1 \标签{119}$$

而且，这也应该是很熟悉的：这是我们陈述的表达式∂C/∂b1的前两个术语。

可以通过监视更改如何在整个网络其余部分中传播来进一步继续。 在每个神经元上，我们选择项σ'（z _j ），并且通过每个权重，我们选择项w _j 。 结果，获得使成本函数的最终变化ΔC _与偏差的初始变化Δb1相关的表达式：

$$

$$\ Delta C \大约\ sigma'（z_1）w_2 \ sigma'（z_2）\ ldots \ sigma'（z_4）\ frac {\部分C} {\部分a_4} \ Delta b_1 \标签{120}$$

将其除以Δb1，就可以得到所需的梯度表达式：

$$

$$\ frac {\部分C} {\部分b_1} = \ sigma'（z_1）w_2 \ sigma'（z_2）\ ldots \ sigma'（z_4）\ frac {\部分C} {\部分a_4} \标签{ 121}美$$

为什么存在渐变衰落问题？

要了解为什么会出现逐渐消失的渐变问题，让我们详细编写渐变的整个表达式：

$$

$$\ frac {\部分C} {\部分b_1} = \ sigma'（z_1）\ w_2 \ sigma'（z_2）\ w_3 \ sigma'（z_3）\，w_4 \ sigma'（z_4）\ \ frac {\部分C} {\部分a_4} \标签{122}$$

除最后一项外，该表达式是形式为w jσ'（z _j ）的项的乘积。 为了了解它们各自的行为，我们看一下函数σ的图形：



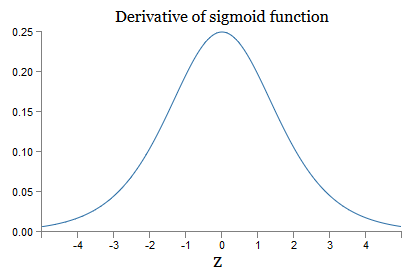
该图在点σ'（0）= 1/4处达到最大值。 如果我们使用标准方法来初始化网络权重，那么我们将使用高斯分布（即均方根零和标准偏差1）来选择权重。因此，通常权重将满足不等式| w _j | <1。 比较所有这些观察结果，我们看到w jσ'（z _j ）项通常将满足不等式| w jσ'（z _j ）| <1/4。 而且，如果我们采用此类术语集的乘积，则它将成倍下降：术语越多，乘积就越小。 它似乎似乎是解决梯度消失问题的可能方法。

为了更准确地写出来，我们将∂C/∂b1的表达式与相对于下一个偏移量（例如∂C/ / b _3）的梯度表达式进行比较。 当然，我们没有写下∂C/∂b3的详细表达式，但是它遵循与上述forC /∂b1相同的定律。 这是两个表达式的比较：



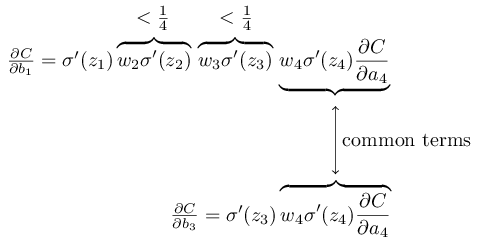
他们有几个共同的成员。 但是，梯度∂C/∂b1包括两个附加项，每个项的形式为w jσ'（z _j ）。 如我们所见，这些项通常不超过1/4。 因此，梯度∂C/∂b1通常比∂C/ 16b ₃小16倍（或更多）。 这是梯度问题消失的主要原因。

当然，这不是准确的，而是问题的非正式证明。 有几个警告。 特别地，人们可能对训练期间权重w _j是否会增加感兴趣。 如果发生这种情况，乘积中的项w jσ'（z _j ）将不再满足不等式| w jσ'（z _j ）| <1/4。 如果结果证明它们足够大，大于1，那么我们将不再面临渐变衰落的问题。 取而代之的是，当您移回图层时，梯度将呈指数增长。 而不是消失的梯度问题，我们得到爆炸性梯度增长的问题。

爆炸梯度增长问题

让我们来看一个爆炸性梯度的特定示例。 该示例有些虚构：我将调整网络参数，以确保发生爆炸性增长。 但是，尽管该示例是人为的，但它的优势在于它清楚地表明，梯度的爆炸性增长不是假设的可能性，而是可以实现的。

要实现爆炸性梯度增长，您需要执行两个步骤。 首先，我们在整个网络中选择较大的权重，例如w1 = w2 = w3 = w4 = 100。 然后我们选择这样的偏移，以使项σ'（z _j ）不会太小。 这很容易做到：我们只需要选择这样的位移，以使每个神经元的加权输入为zj = 0（然后σ'（z _j ）= 1/4）。 因此，例如，我们需要z ₁ = w ₁ a ₀ + b ₁ = 0。 这可以通过设置b ₁ = −100 ∗ a ₀来实现。 可以将相同的想法用于选择其他偏移量。 结果，我们将看到所有项w jσ'（z _j ）等于100 * 14 = 25。 然后我们得到了爆炸性的梯度增长。

不稳定的梯度问题

基本问题不是梯度消失问题或梯度的爆炸性增长。 正是第一层的梯度是所有其他层的成员的乘积。 并且当层数很多时，情况基本上变得不稳定。 所有层都可以以大约相同的速度学习的唯一方法是，选择能够相互平衡的工作人员。 而且在缺乏某种机制或这种平衡的理由的情况下，这不太可能是偶然发生的。简而言之，真正的问题是NS受到不稳定梯度问题的困扰。最后，如果我们使用基于梯度的标准学习技术，则网络的不同层将以截然不同的速度学习。

锻炼身体

• 在讨论消失梯度问题时，我们使用了|σ'（z）| <1/4。假设我们使用不同的激活函数，其导数可能更大。这会帮助我们解决不稳定的渐变问题吗？

普遍存在的衰落梯度问题

我们已经看到，梯度可以在深层网络的第一层消失或爆炸性增长。实际上，当使用乙状神经元时，梯度通常会消失。为了理解原因，再次考虑表达式|wσ'（z）|。为了避免消失的梯度问题，我们需要|wσ'（z）|≥1。您可能会决定使用w的非常大的值很容易实现。但是，实际上并不是那么简单。原因是项σ'（z）也取决于w：σ'（z）=σ'（wa + b），其中a是输入激活。而且，如果将w增大，则需要尽量不要使σ′（wa + b）并行减小。事实证明这是一个严重的限制。原因是当我们使w大时，我们使wa + b非常大。如果看一下σ′的图，可以看出这导致我们进入函数σ′的“翅膀”，它的值很小。避免这种情况的唯一方法是将传入的激活保持在相当窄的值范围内。有时这是偶然发生的。但是更多的情况不会发生。因此，在一般情况下，存在梯度消失的问题。

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

我们研究了每个隐藏层中只有一个神经元的玩具网络。那么在每个隐藏层中都有许多神经元的更复杂的深度网络呢？



实际上，在这种网络中会发生很多相同的事情。在反向传播这一章的前面，我们看到具有L层的网络的＃1层中的梯度指定为：

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

此处的∑'（z ^l）是对角矩阵，其元素是第1层加权输入的σ'（z）值。 w ¹是不同层的权重矩阵。甲∇ _一个 Ç - C中输出的激活偏导数的向量。

这种表达比一个神经元的情况复杂得多。然而，如果你仔细观察，它的本质将是非常相似的，带着一帮对形式的（W的^Ĵ）^牛逼 Σ“（在Z ^Ĵ）。此外，矩阵∑′（z ^j）对角地具有小的值，不大于1/4。如果权重矩阵W ^Ĵ不是太大，每个附加构件（瓦特^Ĵ）^Ť Σ“（Z ^升）会降低梯度向量，从而导致梯度消失。在一般情况下，如我们前面的示例所示，大量的乘法项会导致不稳定的梯度。在实践中，通常凭经验在S型网络中，第一层中的梯度会迅速消失。结果，这些层的学习变慢了。放缓并不是偶然或不便：这是我们选择的学习方法的根本结果。

深度学习的其他障碍

在本章中，我着重讨论渐变的衰落（更常见的是不稳定渐变的情况），它是深度学习的障碍。实际上，不稳定的梯度只是民防发展的一个障碍，尽管这是一个重要而根本的障碍。当前研究的重要部分是试图更好地理解GO教学中可能出现的问题。我不会详细描述所有这些作品，但我想简短地提及几本书，以使您对人们提出的一些问题有所了解。

作为2010年的第一个例子有证据表明，使用S型激活功能会导致学习NS的问题。特别是，发现有证据表明，使用S形将导致以下事实：训练期间最后一个隐藏层的激活在区域0中饱和，这将严重减慢训练速度。已经提出了几种替代激活函数，它们不会受到饱和问题的太大影响（另请参见另一篇讨论文件）。

作为第一个示例，2013年，在GO上研究了随机随机权重下降和权重的随机初始化对基于梯度的下降的影响。在这两种情况下，一个好的选择都会显着影响训练STS的能力。

这些示例表明了一个问题“为什么STS这么难训练？”非常复杂。在本章中，我们重点介绍了与GNS梯度训练相关的不稳定性。前两段的结果表明，激活函数的选择，权重的初始化方法甚至基于梯度下降的训练实施细节也都起作用。而且，当然，网络体系结构和其他超参数的选择将很重要。因此，许多因素可以在学习深度网络的难度中起作用，而了解这些因素的问题是正在进行的研究的主题。但是，所有这些似乎都令人沮丧，并激发了悲观情绪。但是，有个好消息-在下一章中，我们将包装所有对我们有利的东西，并且我们将在GO中开发几种方法，在某种程度上可以克服或规避所有这些问题。