在第一
本出版物中，有人说有一个被遗忘的Erd -s-Renyi定理，据此定理得出，在长度为N的随机序列中，概率接近1，存在一行相同的长度值
。 所指示的随机变量属性可用于回答以下问题：“处理大数据后，残差序列是否服从随机数定律？”
这个问题的答案不是根据与分布正态性的对应关系来确定，而是根据残差序列本身的性质来确定。
通过存在或不存在或转移相同字符的合同的频率。 我试图发布以展示使用此工具的可能性，尽管在进行大数据分析时，它在现实中的工作方式引起了很多疑问。 但是讨论非常有成果，
VDG用户甚至提出了一个真实的例子：
“ ...神经元的树突分支可以表示为位序列。 当在任何位置激活突触链时，都会触发分支，然后触发整个神经元。 神经元的任务分别是不响应白噪声，据我所记得的Numenty，该链的最小长度是锥体神经元中具有其一万个突触的14个突触。 根据公式，我们得到： 。 也就是说，由于自然噪声，将出现长度小于14的链，但不会激活神经元。 这是完全正确的 。
”让我们尝试考虑本材料中介绍的机制。
第一本出版物提出了许多问题。 让我们尝试阐明本文中的Erds-Renyi定理的机理。
解决方案是与
Penny Game悖论有关的。 游戏包括以下内容-两名玩家A和B要掷硬币五次，例如，分配“老鹰” -1，“尾巴” -0。玩家A选择三个值的序列并将其发声，假设为001。
玩家B选择自己的顺序，假设为100。顺序排名第一的玩家是获胜者。 假设01001下降了，即0-100-1，对应于B的选择。“ Penny Game”的悖论是，无论玩家A选择哪种顺序，玩家B总是有机会选择一个顺序，概率更大玩家B的获胜矩阵如图1所示。
图 1.在“一分钱游戏”中，玩家B的回报矩阵为5张。这种自相矛盾的结果是随机序列不是传递的，也就是说，如果U> R，并且R> Q，则这并不意味着Q>U。
如果玩家遵守规则并遵守概率论定律，则这种悖论的结果是以下普通现象：
- 在赌博中，他通常会赢钱，而他的收银员更多-“击碎银行”。
- 在赌场中，只有赌场获胜。
- 在证券交易所交易时，只有运气才能确定交易者将持续多久，直到他失去资本。
“ Penny Game”悖论所基于的这一法则的物理含义是，能够继续随机序列的法则更具优势。 与第一个示例一样-拥有更多现金的玩家。 在第二个选项中-赌场同时玩数百个序列，并且在任何玩家停止游戏后将继续玩。 一场针对一位玩家进行交换的游戏无法与该交易所进行的数百万次操作进行比较。
如您所见，绘制了第一条定律-BigData与本地信息进行比较来确定情况。
第二个关键时刻是缺少随机序列的传递性。 其结果是无法回滚该情况。
BigData分析中的进一步假设：
1）只有在记录了所调查事件的后果的数量上，才可能了解正在发生的事件。 此过程的机制可以表示如下。 随机字段是其中一些潜在过程试图实现自身的字段。 自我实现后，该流程将保留更改，我们尝试从已发生的流程中检测出痕迹的程度。 依赖关系已经由剩余结果的份额大小确定。 我将在上面解释说，我认为，这些转变本身的发生方式，目前，科学还无法给出正式定义。 如果这些定义是正确的，那么芝诺的某些悖论将不再是悖论，而对立统一和斗争，唯物辩证法将不再是其中的假定。
我认为您不应该破坏陈述的矛头，即如果我们根据事实确定流程，那么这是没有意义的练习，因为下一个流程将是不可预测的。 一个人可以在本地看到，并且BigData流程可以持续数十亿年，因此我们有机会从BigData字段中查看流程的机制。
这里介绍了有关宇宙的巨大价值的有趣材料。
2）第二个假设可以从不存在传递性的性质中得出，是区间和条件对所研究过程的影响。 就是说，一方面，有一个时间坐标来定位正在研究的过程，并且几乎没有机会重复我们的过程形成的条件，并收到了数百万条记录。 另一方面，组合定律不可忽略。 这些定律告诉我们，一定会出现某种组合的可能性。 图2显示了N个信号链的变体的分布，其中存在长度为k的子顺序行。 总金额大于
，因为短链与长链相结合。
图 2. N个值序列中k个相同信号的可能子阶变体的数量。对于存在比N / 2长的链的变体，它们用黄色填充，它们的数量可以通过以下公式很简单地确定：
也就是说，包含k> = N / 2个相同值的链的序列的相应概率（我们将不描述一系列N值的概率）将由以下公式确定：
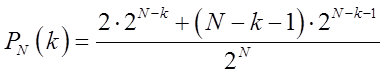
在讨论的第一部分中，提出了一些问题，其实质归结为：“白噪声的边界在哪里？” 这里，考虑图2的表，根据以下方案形成了用于讨论的假设。
基于Muavre-Laplace积分定理：
我们定义f（1.96）= 95％概率的间隔：
如果您看一下，图2中的表反映了概率的完整字段，另一方面，每种情况下的分布参数都是唯一可定义的，如图3所示，我们将其作为一系列9个值的示例进行显示。 自选数量
，对于这种数量的测试，我们将找到alpha。
图 3.同一信号的长度为k的子顺序的概率间隔的边界，按9个值的顺序排列，可靠性为2 sigma（95％）。图4给出了随机变量的间隔，其中图4b是图4a的转置。
图 4.每个子顺序的随机大小间隔，可靠性为95％。为了以某种方式构造白噪声在哪里的问题的答案，他制定了以下现有方法：
- 白噪声被社区认可；
- 可以用分析表达式表达的数据；
- 由神经网络构成的信息；
- 量子比特，量子计算机；
- 大数据
- 如果存在大数据，则完全有可能存在超数据。
对于建议的结构，线索是O. V. Filatov的想法
“将随机二进制序列定义为组合对象。 “随机二元序列中重合片段的计算”，关于类似于微世界中粒子行为的序列片段行为。
具有三维结构的量子位使我们有理由相信结构方案应具有三维模型。 社区认可了几层，暗示了模型的分层，并结合所有这些，以环形的形式，可能是最优雅的方案，图5。
图 5.假设将随机变量映射到空间（从互联网拍摄的图片）中的数据结构。进一步发展推理，我们注意到在图3中，所有频率都是偶数。 这是数据“ 0-1”对称的结果。
所罗门·沃尔夫·哥伦布的 《 哥伦布 假设》中反映了随机数据的对称性。 根据研究Filatova O.V.
“ Golomb假设的公式推导。 一种从Mises频率创建伪随机序列的方法。 “长序列组合”的基础知识使用半波的概念。 我相信这方面对白噪声的研究非常重要，因为它与行长等参数相关。
给定随机过程的性质，白噪声波可以获得各种性质，包括缺乏波
对称性和可能不符合
Noether定理 。 但是，在物理世界中存在一些过程，例如冲浪波泡沫的形成，如图6所示。因此，我们有充分的理由允许白噪声波具有异常的参数。
图 6.海岸附近的波浪形变的机理以及在局部空间中投影到某些超平面上时可能看起来像随机过程的过程示例（从互联网上拍摄的照片）。转向实际部分，我将总结在处理白噪声时提出的方法。
- 随机过程中缺少传递性。
- 假设白噪声的对称性是实现比当前考虑中的过程更高的过程的对称性的实现。
- 随机过程的局部性。 该前提未在出版物中明确显示，但非常适合构造数学框架。 当您编写一个脚本来设置访问存储单元并读取其内容的要求时，都会使用它（建设性数学）。 由于默认情况下，您的意思是在此单元格中存在某个值0或1，因此没有其他值。 这里介绍了熟悉她的方法的好材料：N.N. Nepeyvoda “建设性数学：成就，劣势和教训的回顾。 第一部分“ 。
实践部分
在第一部分中，对Erds-Renyi定理的问题进行了研究，其中包括以下事实：仅在一个来源中找到了该定理，该源是匈牙利语翻译的，这本书在苏联发行，没有发现任何证据或提及。 由于这一事实，其存在以及其应用的总体不确定性。
搜索结果是在Filatov O.V.的工作中发现的。
“ Golomb假设的公式推导。 一种从Mises频率创建伪随机序列的方法。 以下是“长序列组合”的基础知识，第15页，图7，我引用了原始材料。
图 7.出版物Filatova OV的原始部分 “ Golomb假设的公式推导。 一种从Mises频率创建伪随机序列的方法。 “长序列组合”的基础。Erds-Renyi定理的公式如下：
当抛硬币N次时，一排硬币的一系列下降的相等边
观察到的概率趋于1，N趋于无穷大。
我们用“长序列组合”的形式将定理写成硬币的一侧：
我们进行证明：
如您所见，一列由长度相同的信号链组成的火车的米塞斯频率
与随机序列情况下同一链的概率的鄂尔多斯-仁尼定理的结论一致。 因此，您可以消除疑问并认识到它的存在和应用的可能性。
由于该出版物已经得到市场营销人员的更多推荐，因此在下一部分继续，“白噪声绘制了一个黑色正方形。 第3部分。申请。”
其他部分：
第1 部分 ，
第3部分 。