WMS的离散数学：对库存批次进行聚类

本文介绍了在引入WMS系统时如何面对非标准集群问题以及解决该问题的算法。 我们将告诉您如何应用系统，科学的方法解决问题，遇到的困难以及从中学到的教训。

该出版物开始了一系列文章，在这些文章中，我们分享了在仓库流程中实施优化算法的成功经验。 该系列文章的目的是使读者熟悉几乎在任何大中型仓库中出现的优化仓库操作的任务类型，并讲述我们在解决此类问题方面的经验以及通过这种方法遇到的陷阱。 这些文章对在仓库物流行业工作，实施WMS系统的人员以及对企业中的数学应用程序和企业流程优化感兴趣的程序员很有用。

工艺瓶颈

2018年，我们在车里雅宾斯克LD Trading House公司的仓库中实施了一个引入WMS系统的项目。 推出了产品“ 1C物流：仓库管理3”，该产品可用于20个工作： WMS操作员，仓库管理员，叉车司机。 仓库平均约4000平方米，单元数为5000，SKU为4500。仓库存储自己生产的球形阀，尺寸从1千克到400千克不等。 由于需要根据FIFO和产品放置的“在线”详细信息来选择商品，因此仓库中的库存是按批次存储的（以下说明）。

在为仓库流程设计自动化方案时，我们面临着存货非最优存储的问题。 正如我们已经说过的，起重机的堆放和存储具有“行”的细节。 也就是说，单元中的产品一排又一排地堆叠在一起，通常不存在将一块放在一块上的能力（它们只是掉下来，重量也不小）。 因此，事实证明，一个存储单元中只能定位一个批次的一个命名法，否则，如果不“铲除”整个单元，则旧的命名法不能从新的命名法下拔出。

产品每天到达仓库，每次到达都是一个单独的批次。 尽管每个仓库都应存放在一个单独的单元中，但由于仓库运营1个月，总共创建了30个单独的仓库。 通常不是在整个托盘中而是在整件货物中选择货物，因此，在件选择区域中，在许多单元格中可以看到以下图片：在一个容积大于1 m3的单元格中，有几台起重机占据了单元格体积的不到5-10％（见图1）。 ）

图1.单元格中几件商品的照片

面对存储容量使用不足的问题。 可以想象一下灾难的严重程度，我可以举几个数字：在仓库运营的不同时期内，平均有100到300个这样的单元，其中的残留物很少。 由于仓库相对较小，因此在仓库的装载季节中，该因素成为“瓶颈”，极大地限制了仓库的流程。

解决问题的想法

这个想法出现了：将日期最近的一批残渣放到一个批次中，然后将这些天平与一个统一的批次紧密地放在一个单元格中，如果没有足够的空间容纳天平总数，则将它们放在几个单元中。


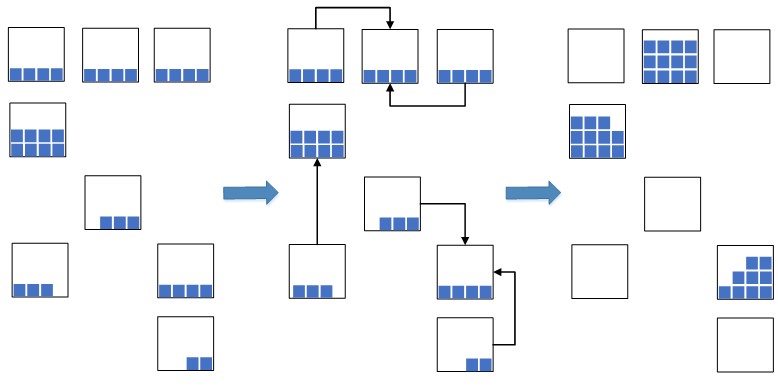图2。 信元压缩方案

这使您可以显着减少将用于新放置货物的仓库占用空间。 在仓库容量超负荷的情况下，这种措施是非常必要的，否则可能根本没有足够的可用空间来放置新货物，这将导致仓库在放置和补货过程中受阻。 以前，在实施WMS系统之前，这种操作是手动执行的，因为在细胞中寻找合适残基的过程相当长，所以这种方法是无效的。 现在，随着WMS系统的推出，他们决定实现流程自动化，加速并使其智能化。

解决此问题的过程分为两个阶段：

• 在第一阶段，我们发现已关闭日期的各方团体；
• 在第二阶段，对于每组批次，我们计算单元中产品残留的最紧凑放置。

在当前文章中，我们将专注于算法的第一阶段，而下一篇文章将覆盖第二阶段的内容。

搜索问题的数学模型

在我们坐下来编写代码和发明自行车之前，我们决定科学地解决这个问题，即：将其数学化，将其简化为众所周知的离散优化问题，并使用有效的现有算法进行求解，或者以这些现有算法为基础进行修改。根据要解决的实际任务的具体情况。

由于它显然是从我们要处理集合的问题的业务陈述中得出的，因此我们根据集合理论来阐述这样的问题。

让 $$$P$-库存中某些商品的所有剩余部分的集合。 让 $$$C$-给定的天数常数。 让 $$$K$-批次的子集，其中子集的所有成对批次的日期差不超过常数 $$$C$。 查找不连续子集的最小数量 $$$K$这样所有子集 $$$K$集体会给很多 $$$P$。

此外，我们不仅需要找到最小数量的子集，还需要找到尽可能大的子集。 这是由于以下事实：在对批次进行聚类之后，我们将“压缩”在单元格中找到的批次的剩余部分。 让我们举例说明。 假设在时间轴上分布有很多参与者，如图3所示。
图3。 多个分区选项

在用相同数量的子集分割集合P的两个选项中，第一个分区（a）对我们的任务最有利。 由于组中的参与方越多，出现的压缩组合越多，因此找到最紧凑的压缩的可能性就越大。 当然，这样的规则无非是一种启发式和我们的推测性假设。 尽管，如计算实验所示，如果考虑到这种最大化条件，则残差后续压缩的紧密度将比不考虑此类条件而构造的压缩平均高出5–10％。

换句话说，简而言之，我们需要找到相似方的组或集群，其中相似性的标准由一个常数确定。 $$$C$。 该任务使我们想起了众所周知的集群问题。 重要的是，所考虑的问题与聚类问题不同，因为在我们的问题中，有一个严格定义的条件，用于由常量确定的聚类元素相似性准则 $$$C$，并且在聚类问题中没有这种情况。 可以在此处找到有关群集问题的说明以及有关此任务的信息。

因此，我们设法提出问题，并以类似的表达方式找到经典问题。 现在，您需要考虑采用众所周知的算法来解决该问题，以免重新发明轮子，而是采取最佳实践并加以应用。 为了解决聚类问题，我们考虑了最流行的算法，即： $$$k$-意味着 $$$c$-装置，用于选择连接组件的算法，最小生成树算法。 可以在此处找到此类算法的描述和分析。

为了解决我们的问题，聚类算法 $$$k$-表示和 $$$c$-means根本不适用，因为簇的数量事先无法得知 $$$k$并且这种算法没有考虑天常数的限制。 这种算法最初被丢弃。
为了解决我们的问题，选择连接组件的算法和最小生成树算法更合适，但是事实证明，它们不能“直接”应用于要解决的问题并获得良好的解决方案。 为了澄清这一点，我们考虑将此类算法的操作逻辑应用于我们的问题。

考虑图 $$$G$顶上有很多派对 $$$P$以及顶点之间的边缘 $$$p_1$和 $$$p_2$重量等于批次之间的天数差 $$$p_1$和 $$$p_2$。 在选择连接组件的算法中，指定了输入参数 $$$R$在哪里 $$$R \ leq C$，并在图中 $$$G$去除了重量的所有边缘均被去除 $$$R$。 只有最接近的对象对保持连接。 该算法的含义是选择一个这样的值 $$$R$，其中图“分解”为几个相连的组件，其中属于这些组件的当事方满足我们的相似性标准，该标准由常数 $$$C$。 生成的组件是群集。

最小生成树算法首先建立在图上 $$$G$最小的生成树，然后依次删除权重最大的边缘，直到图形“分解”为几个相连的组件，其中属于这些组件的批次也将满足我们的相似性标准。 生成的组件将是群集。

当使用这样的算法来解决所考虑的问题时，可能会出现如图4所示的情况。


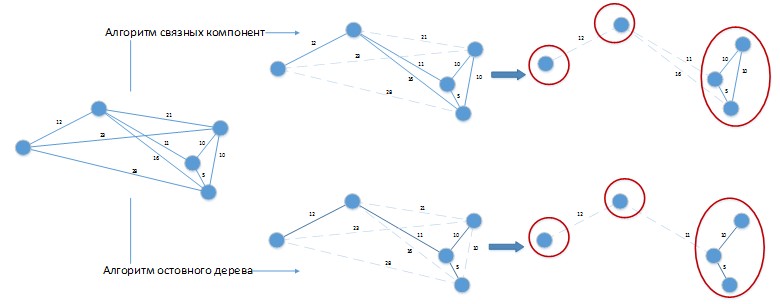图4.聚类算法在解决问题中的应用。

假设我们双方的天数恒定为20天。 数 $$$G$为了方便视觉感知，以空间形式进行了描绘。 两种算法都给出了具有3个群集的解决方案，可以通过将放置在单独群集中的批处理相互组合轻松地进行改进！ 显然，需要根据要解决的问题的具体情况进一步开发此类算法，将其单纯用于解决我们的问题将产生较差的结果。


因此，在开始编写针对我们的任务修改的图形算法代码并发明自己的自行车（已经在其轮廓中猜出了方形车轮的轮廓）之前，我们再次决定科学地解决此问题，即：尝试将其简化为另一个离散问题进行优化，以期无需修改即可应用其解决方案的现有算法。

下次搜索类似的经典问题成功了！ 可以找到一个离散的优化问题，该问题的陈述与我们的陈述几乎是1比1一致。 这个问题原来是覆盖布景的问题 。 我们提出了适用于我们具体情况的问题说明。

有一个有限集 $$$P$和家人 $$$S$的所有不相交的缔约方子集，这样每个子集的所有缔约方对的日期差 $$$我$来自家庭 $$$S$不超过常数 $$$C$。 涂料被称为家庭 $$ 元素所属的最小功率 $$$S$这样集合的并集 $$$我$来自家庭 $$ 应该给所有各方 $$$P$。

有关此问题的详细分析可以在此处和此处找到。 可以在此处找到有关覆盖率问题及其修改的实际应用的其他选项。

所考虑的问题和覆盖集合的经典问题之间的唯一细微差别是需要最大化子集中元素的数量。 当然，可以寻找考虑了这种特殊情况的文章，并且很可能会找到它们。 但是，从下一次搜索文章开始，我们就被一个事实解决了，即解决经典的覆盖集合问题的“贪婪”算法仅考虑子集中元素数量的最大化就建立了一个分区。 因此，我们向前走了一点，现在一切正常。

解决问题的算法

我们已经决定了要解决的问题的数学模型。 现在我们开始考虑该算法的解决方案。 子集 $$$我$来自家庭 $$$S$例如，可以通过这样的过程容易地找到。

1. 步骤0。从集合中安排批次 $$$P$按日期升序排列。 我们认为，各方均未标记为已查看。
2. 步骤1.从尚未查看的聚会中查找日期最少的聚会。
3. 步骤2.对于找到的一方，向右移动，我们将其包括在子集中 $$$我$日期与当前日期相差不超过 $$$C$天。 套装中包含的所有批次 $$$我$标记为已查看。
4. 步骤3.如果在向右移动时不能将下一个批次包含在其中 $$$我$，然后转到步骤1。

覆盖集合的问题是 $$$NP$-困难，这意味着对它的解决方案没有快速的算法（运算时间等于输入数据中的多项式）。 因此，为了解决覆盖集合的问题，选择了一种快速贪婪算法，该算法当然不精确，但具有以下优点：

• 对于小尺寸的问题（这只是我们的情况），它计算的解决方案足够接近最佳值。 随着问题规模的扩大，解决方案的质量下降，但仍然相当缓慢。
• 非常容易实现；
• 快速，因为估计其运行时间为 $$$O（百万）$。

贪心算法根据以下规则选择集合：在每个阶段，选择一个集合，该集合覆盖尚未覆盖的最大元素数。 可以在此处找到该算法及其伪代码的详细说明。 在扰流器中以1C语言实现该算法的可能性较低（有关在下一章中为什么他们开始以“黄色”语言实现该算法的信息）。


当然，这种算法的最佳性是不可能的-启发式算法，更不用说了。 您可以拿出这样的例子，说明这种算法是错误的。 当在某些迭代中，我们发现多个具有相同元素数量的集合并选择出现的第一个元素时，就会出现此类错误，因为该策略是贪婪的：我注意到了第一件事，而“贪婪”得到了满足。

这样的选择很可能会导致随后的迭代结果欠佳。 但是，在大多数情况下，这种简单算法的准确性仍然很高。 如果要更准确地解决问题，则需要使用更复杂的算法，例如在工作中 ：概率贪婪算法，蚁群算法等。 在工作中可以找到将此类算法与生成的随机数据进行比较的结果。

算法的实现与实现

这种算法以1C语言实现，并包含在与“ WMS系统”相连的称为“残渣压缩”的外部处理中。 我们没有在C ++中实现该算法，而是从外部Native组件使用该算法，这会更正确，因为C ++代码的速度是1C中类似代码速度的几倍，在某些示例中甚至是十倍。 在1C中，实施了该算法，以节省开发时间并简化客户工作基础上的调试。 该算法的结果如图6所示。


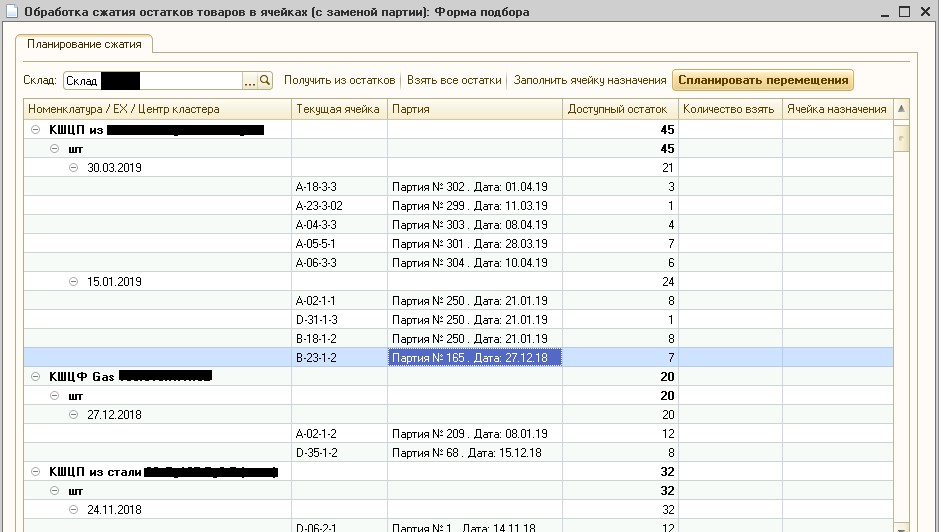图6。 残渣压缩处理

图6显示，在指定的仓库中，存储单元中的当前货物库存被分为几类，其中托运日期相差不超过30天。 由于客户生产和存储金属球阀的保质期为数年，因此可以忽略此日期差异。 请注意，当前此类处理已系统地用于生产中，并且WMS操作员确认批次​​群集的良好质量。

结论和续

我们从解决这样一个实际问题中获得的主要经验是确认使用范例Mat的有效性。 任务陈述 $$$\ rightarrow$著名的垫子。 模型 $$$\ rightarrow$著名算法 $$$\ rightarrow$算法考虑了任务的细节。 离散优化已经有300多年的历史，在此期间，人们设法考虑了很多问题并获得了解决这些问题的丰富经验。 首先，建议您先体验一下这种体验，然后再开始重新发明您的自行车。

同样重要的是，可以不将聚类问题的解决方案与压缩其余批次的问题的解决方案分开考虑，而是一起解决此类问题。 也就是说，选择这样的各方划分到可以提供最佳压缩效果的群集中。 但是出于以下原因，决定对这些问题的解决方案进行划分：

• 算法开发预算有限 。 开发这种通用的，因此更复杂的算法将更加耗时。
• 调试和测试的复杂性。 通用算法在验收阶段将更加难以测试和调试，并且其中的错误将在实时操作中更加困难且调试时间更长。 例如，发生了一个错误，并且不清楚在哪里挖掘：屋面毛毡趋向聚集，屋面毛毡趋向压缩？
• 透明度和可管理性。 这两个任务的分离使压缩过程更加透明，因此对于最终用户-WMS运营商而言更易于管理。 他们可以出于某些原因从压缩中删除某些单元格或编辑可压缩量。

在下一篇文章中，我们将继续讨论优化算法，并考虑最有趣，更复杂的问题：“压缩”单元格中残差的最佳算法，该算法使用从批次聚类算法接收的输入作为输入。

准备了一篇文章
Roman Shanin，项目部程序员，
第一家BIT公司，车里雅宾斯克