所以,想象一下。 五只猫被锁在房间里,为了唤醒主人,他们必须所有人都同意这一点,因为它们只能靠五只猫才能打开门。 如果其中一只猫是薛定inger猫,而其余的猫都不知道其解决方案,那么就会出现一个问题:“他们怎么做到这一点?”
在本文中,我将用一种简单的语言向您介绍分布式系统领域的理论组成及其运行原理。 并且从表面上考虑Paxos'a的主要思想。
当开发人员使用云基础架构,各种数据库,在来自大量节点的集群中工作时,他们可以确保数据将是完整,安全且始终可访问的。 但是保证在哪里?
实际上,我们拥有的保证就是供应商的保证。 它们在文档中的大致描述方式如下:“此服务非常可靠,具有预定义的SLA,请放心,一切都会以您期望的方式以分布式方式工作。”
我们倾向于相信最好的,因为大公司的聪明叔叔向我们保证,一切都会好起来的。 我们不问自己:事实上,为什么它还能起作用? 对于这种系统的正确操作,是否有任何正式的理由?
我最近去
了分布式计算学校 ,这个主题
给我很大的启发。 学校的讲座更像是数学分析课,而不是与计算机系统有关的课。 但这恰恰是一次证明了我们每天不知道使用的最重要算法的方式。
大多数现代分布式系统都使用Paxos共识算法及其各种修改形式。 最酷的是,可以用纸和笔简单地证明该算法的有效性以及原则上存在该算法的可能性。 但是,实际上,该算法用于在云中大量节点上运行的大型系统中。
简要讨论的内容:两位将军的任务让我们来看看
两位将军的热身
任务 。
我们有两个军队-红色和白色。 白色部队驻扎在这座被围困的城市。 由将军A1和A2领导的红色部队位于城市的两侧。 红发女郎的任务是攻击白色城市并获胜。 但是,每个红发将军的军队都比白人小。
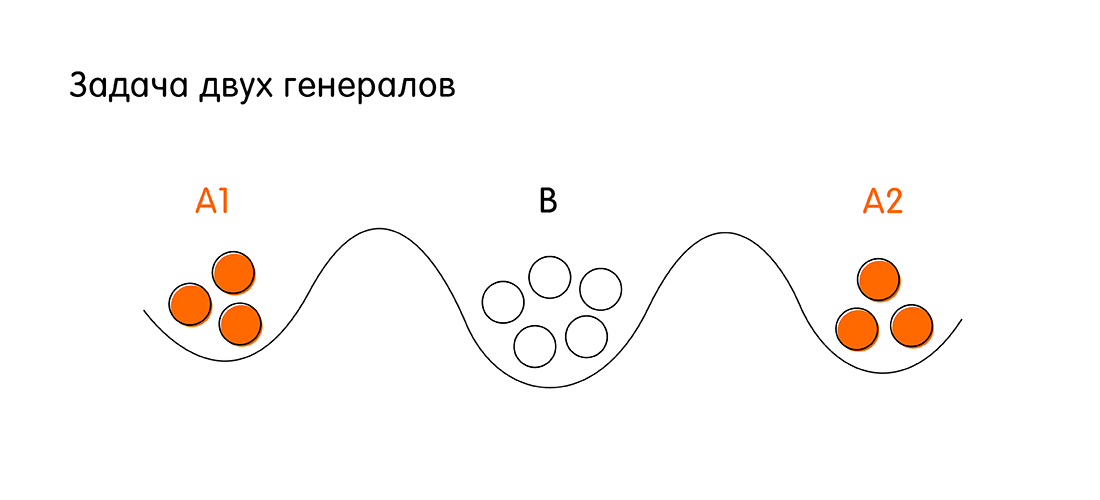
红发胜利的条件:两位将军必须同时进攻才能在数字上获得优于白人的优势。 为此,将军A1和A2需要彼此同意。 如果每个人都单独攻击,则红发将丢失。
为了达成一致,将军A1和A2可以通过白色城市的领土相互派遣使者。 信使可以成功到达盟军将领,也可以被敌人拦截。 问题:红色将军之间是否有这样的通信顺序(从A1到A2发送信使,从A2到A1发送信使的顺序),在这些通信中,保证他们同意在X时发动攻击。在此保证下,可以理解的是,两位将军都将有明确的确认盟友(另一位将军)在指定时间X准确攻击。
假设A1向消息传递者A2发送消息:“让我们今天午夜发动攻击!” 未经将军A2的确认,将军A1不能进攻。 如果信使到达A1,则A2将军发送一条确认消息:“是的,让我们今天填满白人。” 但是现在,A2将军不知道他的使者是否已经到来,也无法保证攻击是否会同时发生。 现在,将军A2需要再次确认。
如果我们进一步安排他们的通讯,结果将是:无论有多少个消息传递周期,都无法保证通知两位将军他们的消息已被接收(只要可以拦截任何信使)。
两位将军的任务很好地说明了一个非常简单的分布式系统,其中有两个节点通信不可靠。 因此我们不能100%保证它们是同步的。 本文稍后将大规模讨论类似问题。
我们介绍分布式系统的概念
分布式系统是一组可以交换消息的计算机(以下称为节点)。 每个单独的节点都是一个自治实体。 一个节点可以独立处理任务,但是为了与其他节点进行交互,它需要发送和接收消息。
消息的具体实现方式,使用的协议-在这种情况下,我们对此并不感兴趣。 分布式系统的节点可以通过发送消息彼此交换数据,这一点很重要。
定义本身看起来并不复杂,但是您需要考虑一个分布式系统具有许多对我们很重要的属性。
分布式系统属性
- 并发 -系统中同时发生或竞争事件的可能性。 而且,我们将认为,在两个不同节点上发生的事件具有潜在的竞争性,只要我们对这些事件的发生顺序没有明确的把握即可。 而且,通常,我们没有它。
- 缺乏全球时钟 。 由于缺少全局时钟,我们没有明确的事件顺序。 在普通的世界中,我们已经习惯了绝对有时间和时间的事实。 对于分布式系统,一切都会改变。 即使是超精密原子钟也有漂移,并且在某些情况下我们无法说出这两个事件中的哪一个发生得较早。 因此,我们也不能依靠时间。
- 系统节点的独立故障 。 还有另一个问题:事情可能不是那么简单,因为我们的节点不是永恒的。 硬盘驱动器可能会发生故障,云中的虚拟机将重新启动,网络可能会闪烁并且消息将会丢失。 此外,当节点正常工作但同时又对系统不利时,可能会出现这种情况。 后一类问题甚至有一个单独的名称: 拜占庭将军问题。 出现此类问题的分布式系统的最流行示例是区块链。 但是今天我们将不考虑这类特殊问题。 我们将对仅一个或多个节点可能发生故障的情况感兴趣。
- 节点之间的通信模型(消息模型) 。 我们已经发现节点通过消息传递进行通信。 有两种众所周知的消息传递模型:同步和异步。
分布式系统中节点之间的通信模型
同步模型 -我们可以肯定地知道存在一个有限的已知时间增量,可以保证该时间增量是一条消息从一个节点到达另一个节点。 如果这个时间过去了,但是消息还没有到达,我们可以放心地说,该节点发生了故障。 在这样的模型中,我们有一个可预测的等待时间。
异步模型 -在异步模型中,我们认为等待时间是有限的,但是没有这样的增量时间,在此之后可以保证节点是不正常的。 即 来自节点的消息等待时间可以任意长。 这是一个重要的定义,我们将进一步讨论。
分布式系统中的共识概念
在正式定义共识的概念之前,让我们考虑一个需要时的情况示例,即
状态机复制 。
我们有一些分布式日志。 我们希望它是一致的,并且在分布式系统的所有节点上都包含相同的数据。 当节点中的一个发现要写入日志的新值时,将其值提供给所有其他节点以使日志在所有节点上更新并系统切换到新的一致状态成为他的任务。 节点之间必须达成共识,这一点很重要:所有节点都同意建议的新值正确,所有节点都接受该值,只有在这种情况下,每个人都可以将新值写入日志。
换句话说:没有节点反对它拥有更多相关信息,并且建议的值不正确。 节点之间的协议和单个正确接受值的协议是分布式系统中的共识。 进一步,我们将讨论允许分布式系统在保证的前提下达成共识的算法。

更正式地说,我们可以将共识算法(或只是共识算法)定义为将分布式系统从状态A转移到状态B的函数。此外,所有节点都可以接受此状态,并且所有节点都可以确认它。 事实证明,这项任务并不像乍看起来那样琐碎。
共识算法属性
共识算法必须具有三个属性,以便系统继续存在并在从状态到状态的转换中具有某种进展:
- 协议 -所有正常工作的节点都必须具有相同的值(在文章中,此属性也被视为安全属性)。 现在,所有正在运行的节点(不会乱序,并且不会与其余节点失去联系)应达成协议,并具有某种最终的一般含义。
在这里重要的是要了解我们正在考虑的分布式系统中的节点要达成共识。 也就是说,我们现在正在谈论的系统可能会发生故障(例如,使某个节点发生故障),但是在该系统中肯定没有任何节点有意与其他节点进行对抗(拜占庭将军的任务)。 由于此属性,系统保持一致。 - 完整性 -如果所有正常工作的节点都提供相同的v值,则每个正常工作的节点都必须接受v的值。
- 终止 -所有正常工作的节点最终都将获得一些值(活动性),这使算法可以在系统中取得进展。 每个正常工作的节点都必须早晚接受最终值并确认:“对我来说,这个值是正确的,我同意整个系统。”
共识算法示例
到目前为止,该算法的属性可能还不十分清楚。 因此,我们以一个示例来说明在具有同步消息传递模型的系统中,最简单的共识算法所经历的阶段,在该模型中,所有节点均按预期运行,消息不会丢失且没有中断(这真的发生了吗?)。
- 这一切都始于求婚(提议)。 假设客户端连接到名为“节点1”的节点并启动了事务,并将新值传递给节点-O。从现在开始,我们将称为“节点1”。 作为提议者,“节点1”现在应该通知整个系统它具有新数据,并且它将向所有其他节点发送消息:“看! 我得到了“ O”值,我想写下来! 请确认您还将在日志中写“ O”。
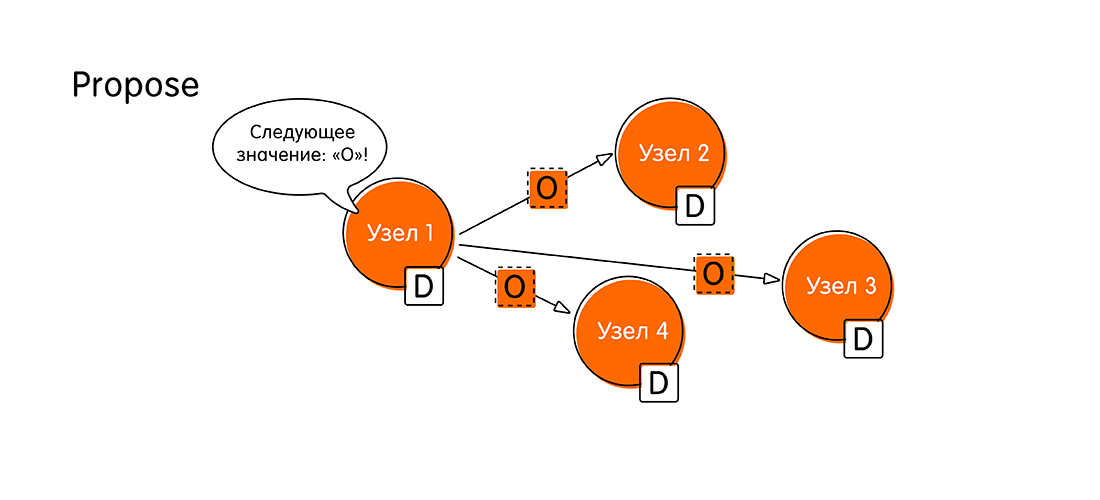
- 下一阶段是投票表决提议的价值(投票)。 这是为了什么 可能发生其他节点接收到更多最新信息,并且它们在同一事务中具有数据的情况。
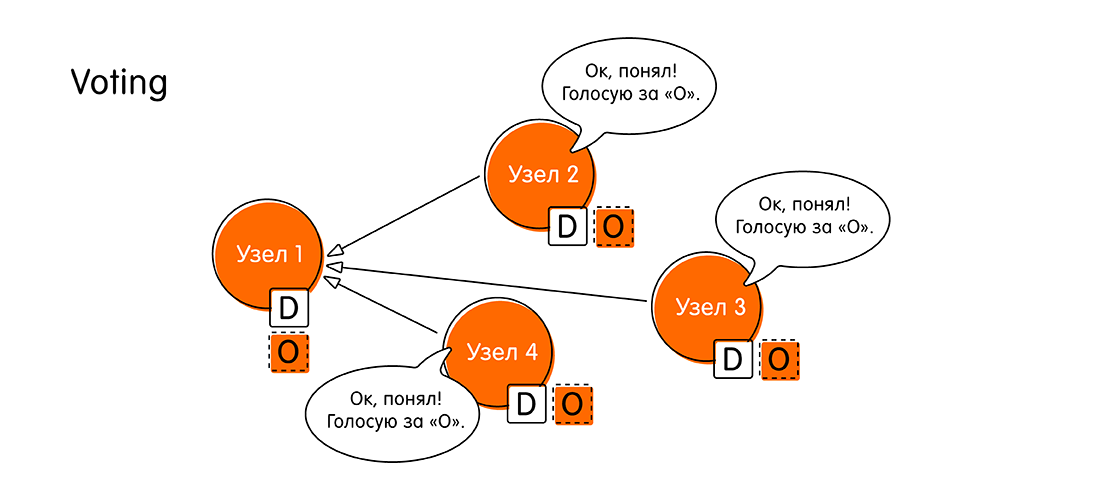
当节点“节点1”发送自己的消息时,其余节点将在其日志中检查此事件的数据。 如果没有矛盾,节点将宣布:“是的,关于此事件,我没有其他数据。 值“ O”是我们应得的最新信息。”
在任何其他情况下,节点都可以回答“节点1”:“听! 我有此交易的最新数据。 不是“哦”,而是更好的东西。”
在投票阶段,节点做出决定:要么每个人都获得相同的价值,要么其中一个投票反对,表明他拥有更多最新数据。 - 如果投票回合成功,并且所有人都赞成,那么系统将进入一个新阶段-接受价值(接受)。 “节点1”收集其他节点的所有响应并报告:“每个人都同意值“ O”! 现在,我正式宣布“ O”是我们的新含义,所有含义都一样! 把自己写在一本小册子里,不要忘记。 写入您的日志!”
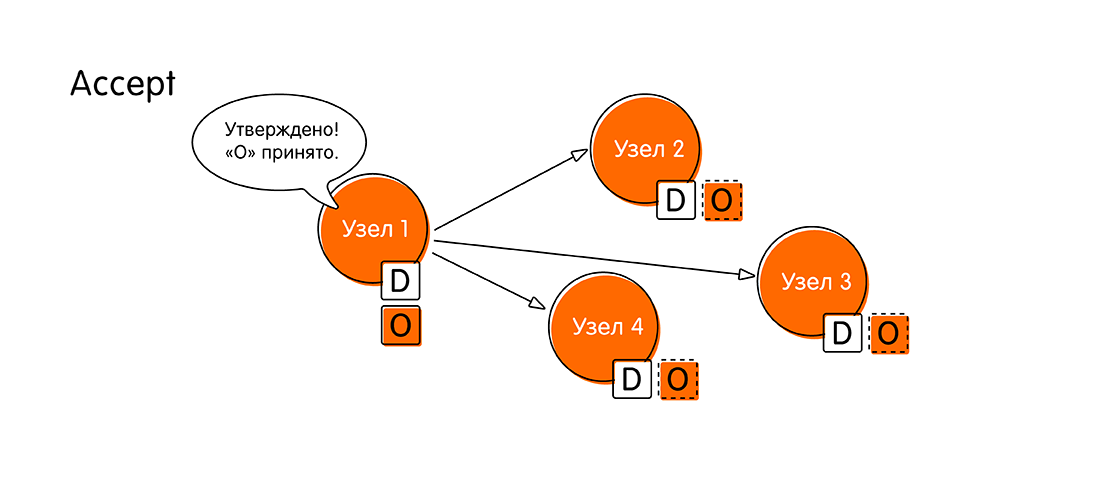
- 其余节点发送一个确认(已接受),确认他们写下了值“ O”,在此期间他们没有设法做任何新的事情(一种两阶段提交)。 在这一重大事件之后,我们认为分布式事务已完成。
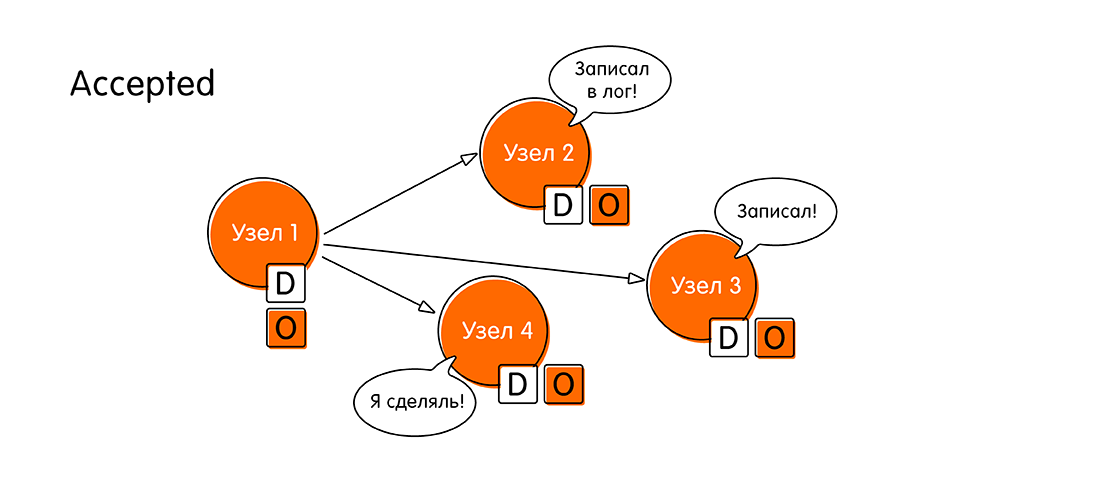
因此,在简单情况下,共识算法包括四个步骤:提议,投票,接受,接受确认。
如果在某些步骤上我们无法达成协议,则考虑拒绝确认建议值的节点提供的信息,重新启动算法。
异步系统中的共识算法
在此之前,一切都很顺利,因为它是关于同步消息传递模型的。 但是我们知道,在现代世界中,我们习惯于异步进行所有操作。 类似的算法在具有异步消息传递模型的系统中如何工作,在该模型中,我们认为来自节点的响应的等待时间可以任意长(顺便说一句,也可以将节点的故障视为一个示例,其中节点可以尽可能地响应) )
既然我们知道了共识算法的基本工作原理,那么问题是那些已经问到这一点的好奇的读者:在一个具有异步消息模型的N个节点的系统中,有多少个节点会发生故障,从而使系统仍然可以达成共识?
剧透背后的正确答案和理由。正确答案是
0 。 如果异步系统中的至少一个节点发生故障,则系统将无法达成共识。 在某些圈子中已知的FLP定理(1985年,Fischer,Lynch,Paterson,与本文末尾的原始链接)上证明了这一主张:“当至少一个节点发生故障时,不可能达成分布式共识”。
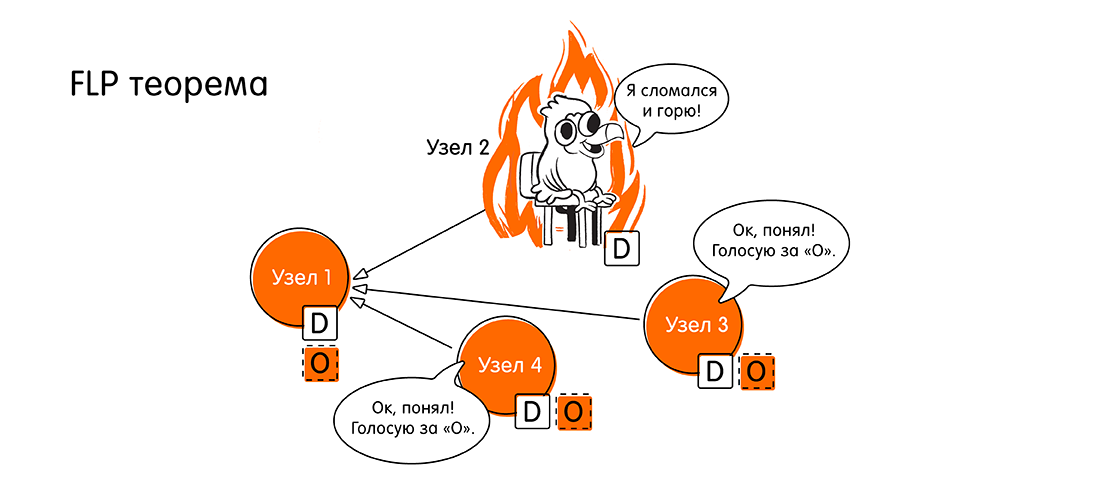
伙计们,那么我们有一个问题,我们已经习惯了一切都与我们异步的事实。 在这里。 如何进一步生活?
我们现在正在谈论理论,关于数学。 从数学语言到我们的工程学是什么意思“无法达成共识”? 这意味着“不能总是实现”,即 在某些情况下,无法达成共识。 这是什么情况?
这只是违反了上述活动性属性。 如果没有来自所有节点的答案,我们没有达成普遍协议,并且系统无法继续运行(无法在有限时间内完成)。 因为在异步系统中,我们没有可预测的响应时间,并且我们无法知道节点是否关闭或仅花费很长时间进行响应。
但实际上,我们可以找到解决方案。 让我们的算法在出现故障的情况下可以长时间工作(它可能无限期地工作)。 但是在大多数情况下,当大多数节点正常运行时,我们将在系统中取得进步。
实际上,我们正在处理部分同步的通信模型。 部分同步的理解如下:在一般情况下,我们有一个异步模型,但是正式地,我们引入了某个时刻的“全局稳定时间”的某种概念。
这个时间点可能不会很长,但是必须有一天。 虚拟警报将响起,从现在开始,我们可以预测消息到达的时间增量。 从这一刻起,系统从异步变为同步。 实际上,我们正在处理此类系统。
Paxos算法解决共识问题
Paxos是一系列算法,可以解决部分同步系统的共识性问题,前提是某些节点可能会发生故障。 Paxos的作者是
Leslie Lamport 。 他在1989年提出了算法存在和正确性的形式证明。
但是证明绝非易事。 该算法的描述仅在1998年发布(33页)。 事实证明,这非常难以理解,2001年,该文章发表了长达14页的解释。 给出大量的出版物是为了表明,事实上,共识问题并非一帆风顺,而这种算法要经受最聪明人的巨大工作。
有趣的是,莱斯利·兰伯特(Leslie Lamport)本人在演讲中指出,在第二篇文章的解释中,有一条陈述,一行(未指定哪一条),可以用不同的方式解释。 因此,大量现代Paxos实现无法正常工作。
对Paxos的工作进行的详细分析将吸引多篇文章,因此,我将尝试简要地介绍该算法的主要思想。 在本文末尾的链接中,您将找到进一步浸入该主题的材料。
Paxos中的角色
Paxos具有角色的概念。 让我们考虑三个主要方面(对其他角色进行了修改):
- 提议者(也可以使用术语:领导者或协调者) 。 这些是从用户那里了解一些新含义并担当领导者角色的人。 他们的任务是发起一轮具有新意义的提案,并协调节点的进一步行动。 此外,Paxos允许在某些情况下有多个领导者在场。
- 接受者(投票者) 。 这些是投票赞成采用或拒绝特定值的节点。 它们的作用非常重要,因为决策取决于它们:在共识算法的下一阶段之后,系统将进入(或不进入)哪种状态。
- 学习者 。 当系统状态更改时,仅接受并记录新接受值的节点。 他们不做决定,只是接收数据并将其提供给最终用户。
一个节点可以在不同情况下组合多个角色。
法定人数概念
我们假设我们有一个
N个节点的系统。 从它们中最多可以出现
F个节点。 如果F个节点发生故障,则集群中必须至少有
2F +1个受体节点。
这是必要的,这样即使在最坏的情况下,我们也始终拥有“良好”的,正常工作的节点。 也就是说,
F + 1个同意的“好”节点,最终值将被接受。 否则,可能会出现不同的本地群体具有不同含义且无法在彼此之间达成共识的情况。 因此,我们需要绝对多数才能赢得投票。
Paxos共识算法的一般思想
Paxos算法涉及两个大阶段,每个阶段又分为两个步骤:
- 阶段1a:准备 。 在准备阶段,组长(提议者)通知所有节点:“我们正在开始一个新的投票阶段。 我们有新一轮。 此回合的编号为n。 现在我们将开始投票。” 目前,它仅报告新周期的开始,但不报告新值。 此阶段的任务是发起新一轮并告诉所有人其唯一编号。 轮数很重要,它的值必须大于以前所有领导人的所有先前投票数字。 由于正是由于整数的原因,系统中的其他节点才能了解领导者数据的新鲜程度。 其他节点可能已经在以后的回合中获得了投票结果,它们只会告诉领导者他落后于时代。
- 阶段1b:承诺 。 当接受者节点收到新投票阶段的编号时,可能会有两个结果:
- n , , acceptor. acceptor , , n. acceptor - (.. - ), , .
- , acceptor , .
- Phase 2a: Accept . ( ) , , :
- acceptor' , . c . x, : «Accept (n, x)», – Propose, – , .. , , .
- acceptor' , , , , . y. : «Accept (n, y)», .
- Phase 2b: Accepted . , -acceptor', «Accept(...)», ( , ) , - () n' > n , .
, , . ! , , .
Paxos. , , , .
, Paxos — , , ,
Raft ,
.
«»:
« »:
- Impossibility of Distributed Consensus with One Faulty Process (FLP impossibility) , Fischer, Lynch and Paterson, research paper, 1985
- The Part-Time Parliament , Leslie Lamport, research paper, 1998
- Paxos made simple , Leslie Lamport, research paper, 2001