在本文中，我们将描述如何开发一种算法，用于对单元格中剩余货物进行最佳压缩。 我们将告诉您如何选择框架动物园环境的必要元启发法：禁忌搜索，遗传算法，蚁群等。
我们将进行计算实验，以分析算法的运行时间和准确性。 我们总结并总结了解决客户业务流程中“智能技术”的优化和实施这一问题所获得的宝贵经验。
本文将对那些实施智能技术，在仓库或生产物流行业中工作的人以及对企业中业务和流程优化中的数学应用程序感兴趣的程序员很有用。
入门部分
该出版物继续了系列文章，我们分享了在仓库流程中实施优化算法的成功经验。 以前的出版物：
如何阅读文章。 如果阅读了以前的文章，则可以立即进入“开发用于解决问题的算法”一章，如果没有，那么下面将介绍扰流板中要解决的问题。
客户仓库要解决的问题的描述工艺瓶颈
2018年，我们在车里雅宾斯克LD Trading House公司的仓库中实施了一个引入
WMS系统的项目。 推出了产品“ 1C物流：仓库管理3”，该产品可用于20个工作：
WMS操作员，仓库管理员，叉车司机。 仓库平均约4000平方米，单元数为5000，SKU为4500。仓库存储自己生产的球形阀，尺寸从1千克到400千克不等。 由于需要根据FIFO和产品放置的“在线”详细信息来选择商品，因此仓库中的库存是按批次存储的（以下说明）。
在为仓库流程设计自动化方案时，我们面临着存货非最优存储的问题。 正如我们已经说过的，起重机的堆放和存储具有“行”的细节。 也就是说，单元中的产品一排又一排地堆叠在一起，通常不存在将一块放在一块上的能力（它们只是掉下来，重量也不小）。 因此，事实证明，一个存储单元中只能定位一个批次的一个命名法，否则，如果不“铲除”整个单元，则旧的命名法不能从新的命名法下拔出。
产品每天到达仓库，每次到达都是一个单独的批次。 尽管每个仓库都应存放在一个单独的单元中，但由于仓库运营1个月，总共创建了30个单独的仓库。 通常不是在整个托盘中而是在整件货物中选择货物，因此，在件选择区域中，在许多单元格中可以看到以下图片：在一个容积大于1 m3的单元格中，有几台起重机占据了单元格体积的不到5-10％（见图1）。 ）
图1.单元中几张照片面对存储容量使用不足的问题。 可以想象一下灾难的严重程度，我可以举几个数字：在仓库运营的不同时期内，平均有100到300个这样的单元，其中的残留物很少。 由于仓库相对较小，因此在仓库的装载季节，该因素成为“瓶颈”，极大地限制了仓库的验收和运输过程。
解决问题的想法
这个想法出现了：将日期最近的一批残渣放到一个批次中，然后将这些天平与一个统一的批次紧密地放在一个单元格中，如果没有足够的空间容纳天平总数，则将它们放在几个单元中。 这种“压缩”的示例如图2所示。
图2。 信元压缩方案这使您可以显着减少将用于新放置货物的仓库占用空间。 在仓库容量超负荷的情况下，这种措施是非常必要的，否则可能根本没有足够的可用空间来放置新货物，这将导致在仓库的放置和补货过程中出现塞子，从而导致接受和装运塞子。 以前，在引入WMS系统之前，这种操作是手动执行的，因为在细胞中寻找合适的残基的过程相当长，所以这种方法是无效的。 现在，随着WMS系统的推出，他们决定实现流程自动化，加速并使其智能化。
解决此问题的过程分为两个阶段：
- 在第一阶段，我们发现要压缩的日期最近的各方组（这是该奉献任务的第一篇文章 ）；
- 在第二阶段，对于每组批次，我们计算单元中产品残留的最紧凑放置。
在当前的文章中，我们以解决过程第二阶段的描述作为结束，并直接考虑优化算法本身。
开发解决问题的算法
在继续对优化算法进行直接描述之前，有必要说一下开发这种算法的主要标准，这些主要标准是实施
WMS系统的项目的一部分。
- 首先，该算法应易于理解 。 这是一个自然的要求，因为假定将来该算法将由客户的IT服务支持并进一步开发，而这通常离数学的精妙和智慧还很远。
- 其次，该算法应该是快速的 。 压缩过程几乎涉及仓库中的所有商品（大约3,000件），对于每种商品，必须解决大约10x100的尺寸问题。
- 第三，该算法必须计算接近于最优的解。
- 第四，算法的设计，实现，调试，分析和内部测试的时间相对较少。 这是一项基本要求，因为包括此任务在内的项目预算 是有限的 。
值得一提的是，迄今为止，数学家已经开发出许多有效的算法来解决单源容量设施定位问题。 考虑可用算法的主要种类。
一些最有效的算法是基于所谓的拉格朗日松弛法的。 通常，这些算法是相当复杂的算法，对于不专心于离散优化的精妙之处的人来说，很难理解。 带有复杂但有效的拉格朗日松弛算法的“黑匣子”不适合客户。
有相当有效的元启发法（
这里是什么元启发法，
这里是什么启发法），例如遗传算法，模拟退火算法，蚁群算法，禁忌搜索算法和其他（可以在
这里找到这种元启发法的概述）。 但是这样的算法已经满足了客户的需求，因为：
- 能够计算非常接近最优的问题的解决方案。
- 足够简单，易于理解，进一步支持，调试和完善。
- 他们可以快速计算出问题的解决方案。
决定使用元启发法。 现在，仍然需要在著名的元启发式方法的大型“动物园”中选择一个“框架”来解决单源容量设施定位问题。 在回顾了许多分析各种元启发式方法有效性的文章后，我们选择了GRASP算法，因为与其他元启发式方法相比，它在计算出的问题解决方案的准确性方面显示了相当不错的结果，是最快的方法之一，最重要的是，它具有最简单的方法和透明的逻辑。
本文详细介绍了与单源容量设施定位问题任务
有关的GRASP算法方案 。 该算法的一般方案如下。
- 阶段1.通过贪婪随机算法生成一些可行的解决方案。
- 第2阶段。在许多社区中使用本地搜索算法改进第1阶段的结果解决方案。
- 如果满足停止条件，则完成算法，否则转到步骤1。在找到的所有解决方案中，总成本最低的解决方案将是算法的结果。
停止算法的条件可以是对迭代次数的简单限制或对迭代次数的限制，而对解决方案没有任何改进。
算法通用方案代码int computeProblemSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolution, int **aMatAssignmentSolution) {
让我们更详细地考虑在阶段1的
贪婪随机算法的操作。可以相信，一开始并没有选择单个单元容器。
- 步骤1.对于当前未选择的每个容器单元格，将计算该值 F′i 成本公式
F′i= fracFiN，
在哪里 F′i -选择集装箱的费用金额 我 以及从中转移货物的总费用 N 尚未连接到任何容器的细胞进入容器 我 。 这样的 N 选择单元格以使其中的货物总量不超过容器的容量 我 。 顺序选择供体细胞以移入容器中 我 为了增加将一定数量的货物移入集装箱的成本 我 。 进行单元选择，直到超出容器容量为止。 - 步骤2.形成的集合 R 具有功能值的容器 F 不超过阈值 \最小（F） cdot（1+a） 在哪里 一 在我们的例子中是0.2。
- 步骤3。从集合中随机 R 选择容器 我 。 N 容器中先前选择的单元格 我 在步骤1中，最终将它们分配给这样的容器，并且不再进一步参与贪婪算法的计算。
- 步骤4.如果所有供体细胞都分配给了容器，则贪婪算法将停止其工作，否则将返回步骤1。
每次迭代时，随机算法都试图以这样一种方式构造解决方案：在构造的解决方案质量和多样性之间取得平衡。 开始决策的这两个要求是算法成功运行的关键条件，因为：
- 如果解决方案的质量很差，那么第二阶段的后续改进将不会产生明显的结果，因为即使改进了质量不好的解决方案，我们也常常会得到同样质量差的解决方案；
- 如果所有解决方案都是好的，但是相同，那么本地搜索过程将收敛到相同的解决方案，这绝不是最佳解决方案。 这种效果称为达到局部最小值，应始终避免。
贪婪随机算法代码 void findGreedyRandomSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int *aFreeContainersFitnessFunction, bool isOldSolution) {
在阶段1构建“开始”解决方案之后，算法将进行到阶段2，在此阶段对发现的解决方案进行改进，其中改进自然意味着降低了总成本。 步骤2中
的本地搜索算法的逻辑如下。
- 步骤1.对于当前解决方案 S 所有“邻居”解决方案都是根据某种邻居构造的 N1 ， N2 ，...， N5 对于每个“相邻”解决方案，都会计算总成本的值。
- 步骤2。如果在相邻解决方案中有更好的解决方案 S1 比原来的解决方案 S 然后 S 假定相等 S1 然后算法进行到步骤1。否则，如果相邻解决方案中没有比原始解决方案更好的解决方案，则邻域的视图将更改为先前未考虑的新解决方案，并且算法进入步骤1。如果考虑了邻域的所有可用视图，但均失败了找到比原始解决方案更好的解决方案，该算法结束了工作。
从以下堆栈中依次选择周围的景观：
N1 ，
N2 ，
N3 ，
N4 ，
N5 。 周围地区的景观分为两种类型：第一类（邻里）
N1 ，
N2 ，
N3 ），其中许多容器没有变化，但只有用于附着供体细胞的选项发生了变化； 第二类（邻居
N4 ，
N5 ），不仅会更改将单元格附加到容器的选项，还会更改许多容器本身。
我们表示
|J| -集合中的元素数
J 。 下图描述
了第一种类型的社区的选项。
图 7.邻里 N1邻里
N1 （或
移位邻域）：包含通过更改仅一个供体细胞到容器的附着来解决与原始问题不同的所有选项。 邻里大小不再
|J| 选项。
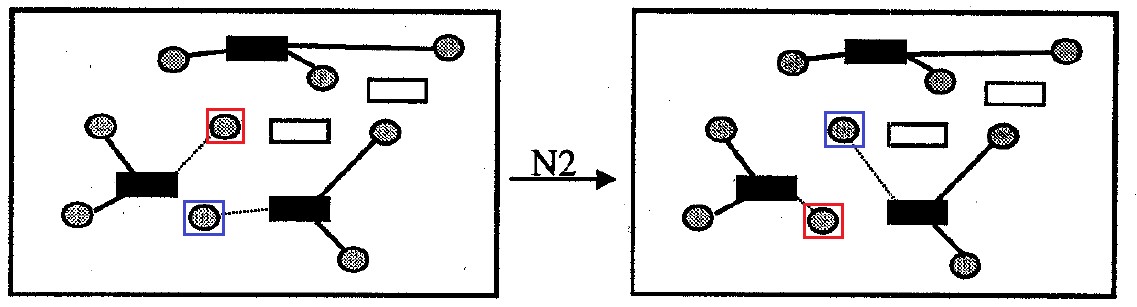图 8.邻里 N2N1附近的本地搜索算法的代码 void findBestSolutionInNeighborhoodN1(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int totalDemand, bool stayFeasible) {
邻里
N2 （或
交换邻域）：包含解决问题的所有选项，它们与原始选项的不同之处在于，一对供体细胞相互交换容器附着。 邻里大小不再
|J|2 选项。
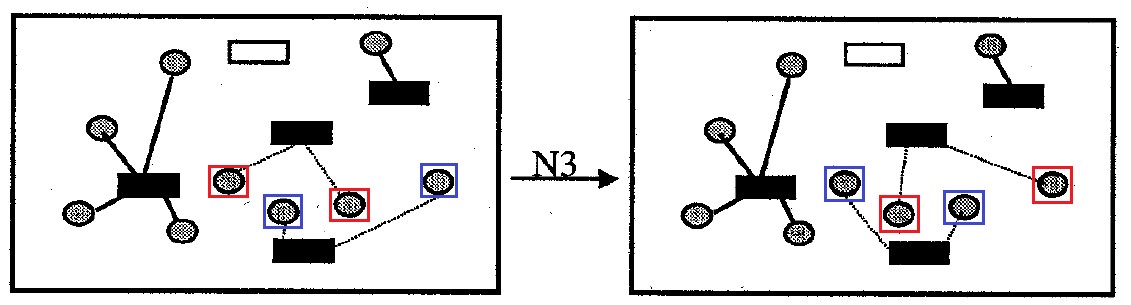图 9.邻里 N3邻里
N3 ：包含解决该问题的所有选项，与原来的选项有所不同，方法是相互替换一对容器中所有单元的附着。 邻里大小不再
|I| 选项。
当已经不可能通过搜索第一类型的“近邻”邻域获得改善时，
第二种邻域被认为是决策“多样化”的机制。
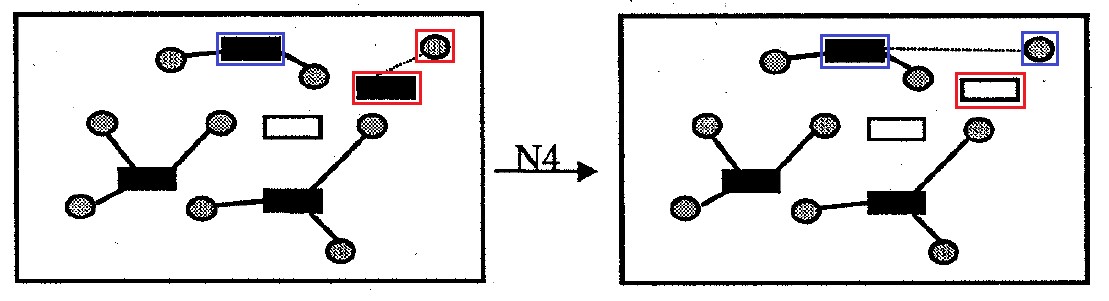图 10.邻里 N4邻里
N4 ：包含从解决方案中删除一个容器单元来解决与原始问题不同的所有选项。 附着在从溶液中移出的这种容器上的供体细胞被附着在其他容器上，以最大程度地减少运输成本和对超过容器容量的惩罚。 邻里大小不再
|I| 选项。
图 11.邻里 N5邻里
N5 ：包含用于解决问题的所有选项，这些选项与原始选项不同，方法是从一个容器中分离单元格，然后将此类单元格附加到任意一对容器的另一个空容器上。 邻里大小不再
|I|2 选项。
该文章的作者说，基于计算实验的结果，最好的选择是首先搜索第一种类型的“近”邻域，然后搜索“远”邻域。
请注意，本文的作者建议在附近进行搜索，而不必考虑每个容器的容量限制。 相反，如果超出了容器的容量，则在解决方案的总成本中增加一些正数的“精细”量，与其他解决方案相比，这将损害这种解决方案的吸引力。 唯一的限制是对容器的总体积，即从供体细胞运输的货物的总体积不应超过容器的总容量。 之所以取消限制，是因为如果考虑到限制，则邻域通常将不会包含一个可接受的解决方案，并且本地搜索算法将在启动后立即完成其工作，而无需进行任何改进。 图12显示了本地搜索操作的示例，其中未考虑每个容器的容量限制。
图 12.在不考虑每个集装箱容量限制的情况下进行本地搜索的工作在该图中，假定来自某些供体细胞的红色和绿色残留物无助于移至除第二个容器之外的任何其他容器。 这意味着无法进一步改进该解决方案，因为在考虑到容量限制的情况下，针对该问题的任何其他新的可行解决方案在运输成本方面将比原始解决方案差。 如您所见，尽管第一个迭代构建了一个容量过大的无效解决方案，但用于2次迭代的算法所构建的可行解决方案要比原始算法好得多。
请注意，这种针对解决方案的不可接受性引入“惩罚”的方法在离散优化中非常普遍，并且经常用于遗传算法，禁忌搜索等算法中。
在完成本地搜索算法后，如果找到的解决方案仍然不可接受，也就是说，某个地方已经超出了集装箱的容量限制，那么我们必须将找到的解决方案采用可接受的形式，并遵守所有对集装箱容量的限制。 解决解决方案不可接受性的算法如下。
- 步骤1.在shift和swap的邻域上执行本地搜索。 在这种情况下，仅在那些恰好减少“罚款”金额的决定中执行过渡。 如果无法减少惩罚，则选择总成本较低的解决方案。 如果无法通过本地搜索进一步改善，请转到步骤2，否则，如果所得解决方案有效，则请完成算法。
- 步骤2.如果解决方案仍然不可接受，则从容量过剩的每个容器中，按照货物体积增加的顺序，分离供体细胞，直到满足容量限制。 对于这种分离的单元格，从第一步开始就重复了算法的所有步骤，尽管事实是许多可用的选定容器以及将剩余单元格附加到它们的方法是固定的，无法更改。 请注意，极少需要执行此步骤2（如计算实验所示）。
计算实验与算法效率分析
GRASP算法是从头开始在
C ++中实现的 ，因为我们没有找到
本文所述算法的源代码。 程序代码是使用带有+ O2优化选项的g ++编译的。
Visual Studio项目代码在
GitHub上
可用 。 客户唯一要问的是出于知识产权，商业机密等原因，删除一些最复杂的本地搜索程序。
在描述GRASP算法的
文章中 ，提到了它的高效率，其中效率意味着它可以稳定地计算出非常接近最优值的解，并且可以很快地工作。 为了验证这种GRASP算法的真实有效性，我们进行了自己的计算实验。 问题的输入数据是我们随机生成的，分布均匀。 将算法计算出的解与最优解进行比较，最优解是通过
本文提出的精确算法来计算的。 可以在GitHub上免费获得这种精确算法的来源，以供
参考 。 任务的尺寸（例如10x100）将意味着我们有10个供体单元和100个容器单元。
计算是在具有以下特征的个人计算机上进行的：CPU 2.50 GHz，Intel Core i5-3210M，8 GB RAM，操作系统Windows 10（x64）。
表3. GRASP算法和精确算法的运行时间比较从表3中可以看出，GRASP算法实际上计算出了接近最优解的值，并且随着问题规模的增加，算法解的质量也会稍有下降。从实验结果还可以看出，GRASP算法相当快，例如，它平均可以在0.5秒内解决10x100尺寸问题。最后值得一提的是，我们的计算实验结果与本文的结果一致。在生产中运行算法
在算法的开发，调试和计算实验中测试之后，就该将其投入运行了。该算法用C ++实现，并放置在DLL中，该DLL 作为Native类型的外部组件连接到1C应用程序。在此处阅读有关外部组件1C的信息，以及如何正确开发它们并将其连接到1C应用程序。在程序“ 1C：仓库管理3”中，开发了一种处理表格，用户可以在该表格中使用所需参数启动压缩残渣的过程。表单的屏幕截图如下所示。图13 附录1C：仓库管理中“压缩”余额的程序形式
用户可以选择以下形式的残留物压缩参数：- 压缩模式：带批处理的群集（请参阅第一篇文章），没有它。
- 仓库，必须在其中的单元中进行压缩。在一个房间里，可以有多个仓库供不同的组织使用。我们的客户就是这种情况。
- 此外，如果用户出于某种原因希望其不参与压缩程序，则用户可以交互地调整从供体单元转移到容器的货物数量，并从列表中删除该项目以进行压缩。
结论
在本文的结尾，我想总结一下由于引入了这种优化算法而获得的经验。- . : , , . - :
- , ;
- .
- ( ), , . «», - . , , . , , , - , .
- , ( ), . , , . , . . , .
- :
- .
- .
- . , .
- . , . , , , , .
- , . ( ) . , .
- .
而且，我认为，最重要的是。企业中的优化过程通常必须在信息化过程完成之后进行。没有初步信息化的优化几乎没有用，因为没有地方可以从中获取数据，也没有地方可以写入算法的解决方案数据。我认为，大多数国内大中型企业已经关闭了自动化和信息化的基本需求，并准备进行流程优化的更多“微调”。因此，我们在实施信息系统之后进行实践，例如ERP，WMS，TMS等。多赚一点。项目，以优化那些在信息系统的实施过程中被认为对客户有问题和重要的过程。我认为这是一种有前途的做法，在未来几年中将会获得发展。
, ,
, .