考虑到对控制对象的一些评论,本材料是根据过去对单身汉的最终资格工作的辩护而创建的。 该材料被创建为同一主题的可能硕士学位论文的初始储备。
现代磁悬浮系统越来越广泛地被使用:高速旅客列车,对振动敏感的机构的隔离,磁性轴承,感应炉中熔融金属的悬浮以及金属坯的悬浮。 近来,磁悬浮效应也被用在家用设备中。

也许最重要的应用是在带有超导悬浮系统的火车上。 这是由于诸如更高的可靠性(由于没有摩擦),相对较低的功耗以及高速开发的能力等优点所致。
但是,由于描述物体动力学的物体运动的非线性方程式,很难再现控制物体的过程。 它大约是物体相对于零标记的位置(距离)。
简而言之,磁悬浮是物体在重力场中一定距离处的稳定位置,通常,重力加速度由物体的加速度补偿,该加速度是由磁场产生的。 在这种情况下,产生提升力。
利用反磁性,涡流系统和超导体以及伺服机构来实现磁悬浮。
在当前文章中(削减),我们将考虑对磁悬浮线性化系统进行模态控制,以及对系统的非线性模型进行模态控制。
数学模型
考虑一个简单的磁悬浮方案。
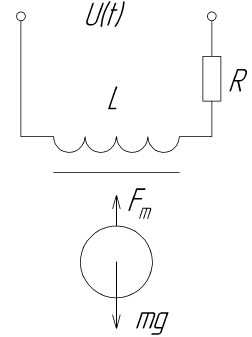
该图显示了与控制对象的磁场相互作用的电磁体,该控制对象是球形永磁体。 通过改变电磁体的吸引力,可以实现悬浮效果。
在最后的工作中,考虑了一个二阶对象,其中一个重要分量,即线圈中的电流未包含在状态向量中。 这次将介绍此组件。
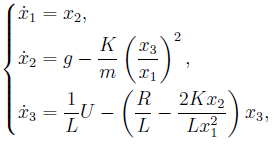
在哪里 -物体的位置;
-物体位置的变化率;
-重力加速度;
是一个常数;
-球物体的质量;
-线圈中的电流;
-线圈电感;
 -输入电压;
-输入电压;
-线圈的有源电阻。
上面的一些变量的值汇总在一个表中。
为了获得线性模型,应该线性化方程组。
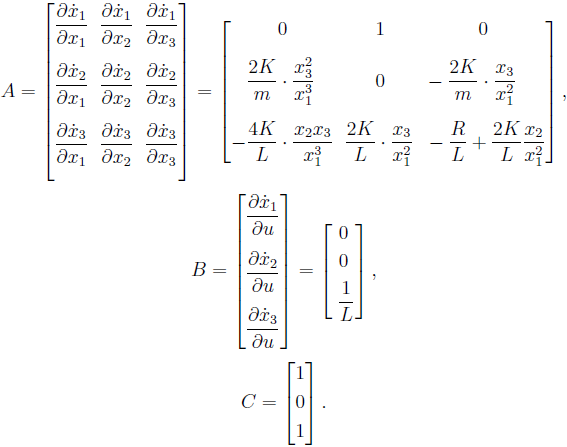
矩阵视图 可以通过以下事实证明这一点:状态向量变量如position( )和当前( )
以这种形式,所得矩阵仍然不适合建模。 为此,我们设置了初始条件。
x_1 ^ {\左\ {0 \右\}} = 0.005,〜x_2 ^ {\左\ {0 \右\}} = 0
g-\ frac {K(x_3 ^ {\左\ {0 \右\}})^ 2} {m(x_1 ^ {\左\ {0 \右\}})^ 2} = 0
x_3 ^ {\左\ {0 \右\}} = \ sqrt {\ frac {gm} {K}} x_1 ^ {\左\ {0 \右\}} = 0.063〜\文本{A}
现在替换获得的数据并 x_3 ^ {\左\ {0 \右\}} 在初始时间查找输入信号的值:
U ^ {\左\ {0 \右\}} = \左(R-\ frac {2Kx_2 ^ {\左\ {0 \右\}}}} {(x_1 ^ {\左\ {0 \右\ }})^ 2} \右)x_3 ^ {\左\ {0 \右\}} = Rx_3 ^ {\左\ {0 \右\}} = 1.95〜\文本{B}。
造型
现在,您可以合成控件。 为了进行研究,选择了Matlab软件包。 以下是用于按状态获取调节器系数的代码:
g = 9.81; K = 0.659*10^-3; m = 0.0106; L = 0.109; R = 31.1; x10 = 0.005; x20 = 0; x30 = sqrt(g*m/K)*x10; u = R*x30; A = [0 1 0; 2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2); -4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)]; B = [0; 0; 1/L]; C = [1 0 0]; W = ctrb(A, B);
要了解是否有可能为结果系统综合控制,您需要了解可控性矩阵,并根据该矩阵得出结论:
>> detW detW = -7.5351e+07
行列式为非零;因此,线性化系统是可控制的。
矢量极是包含磁悬浮线性化系统的所需极的矢量。
以单步形式应用测试效果时,我们获得以下结果:
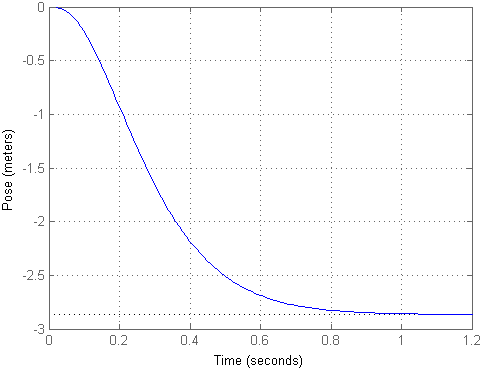
如您所见,事实证明,尽管该对象保持在相同的位置,但它却飞行了相当长的距离而几乎没有撞击。 为了使输入与输出相对应,我们可以计算比例因子km并将其乘以输入信号,这是在第二个模型中实现的。 然后过渡过程将如下所示:
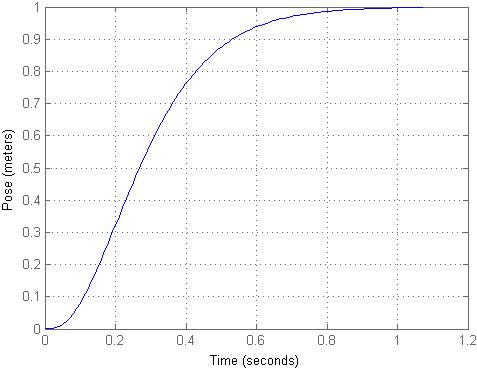
对于这样的安装,最终位置仍然很大。 现在,让我们忽略当前电流,直接进入Simulink模型,在此我们考虑剩余的事情。
我们缩放输入信号,以便方便地以厘米为单位表示输出值。 我们将几种测试动作应用于输入,以检查系统中的瞬态外观以及流过的电流。
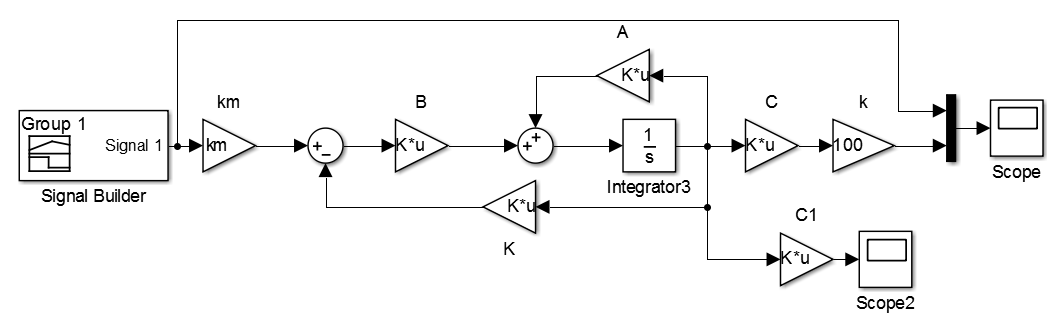
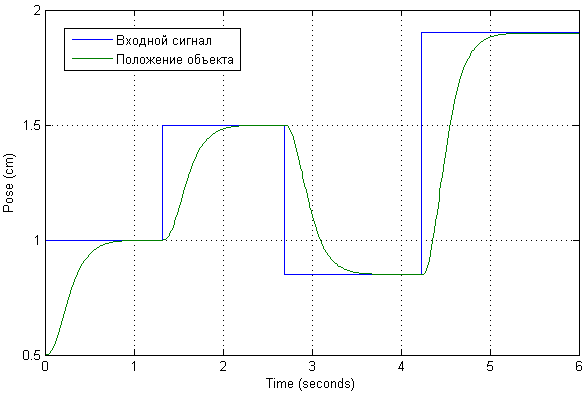
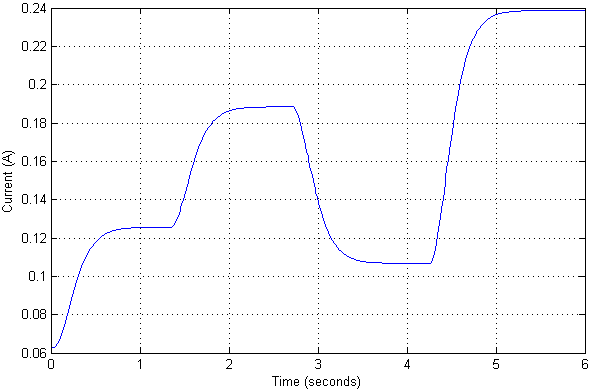
事实证明,在对象的这些位置处的当前值不是那么重要。 瞬态本身本身就是非周期性的,没有过冲和静态误差。 实际上,它是由调整后系统的所需极点设置的。
但是,在工作点上的这种近似可能无法与原始非线性模型一起正常工作。 检查一下。 具有连接的控制器的非线性系统模型如下所示。

这是所有实验后剩下的最终版本。 限制输入电压(0-12V)和物体本身的位置(0-4cm)。 排除了调节器的第二个组成部分,因为它的过渡过程不稳定:

更改电路后,瞬态现在看起来像这样:
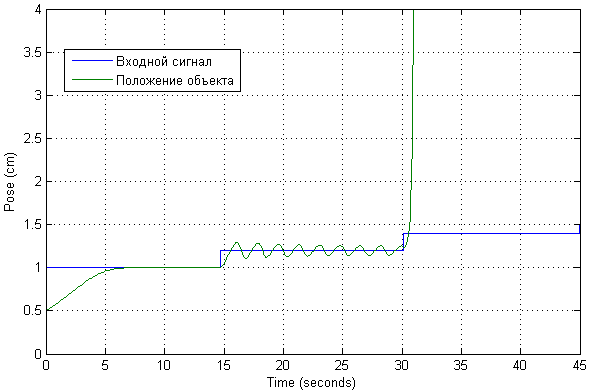
立即检查了这种系统的可能操作范围。 您会看到所需的位置将与起点稍有偏差。 在这种情况下,可能出现明显的振荡。
在这种情况下,当前值如下:
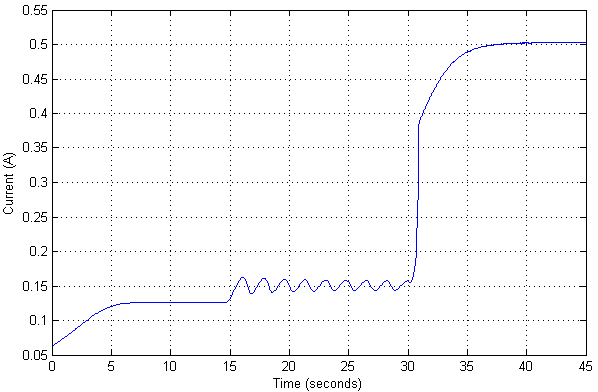
由于已经检查了对象的非线性模型,因此您也可以查看对象的最大位置值可以达到的最大值,而该位置仍不会失去稳定性。
在使用不同的输入信号进行建模后,注意到线性化模型非常好。 因此,在这里我们将根据初始输入信号增加10倍来演示瞬态。
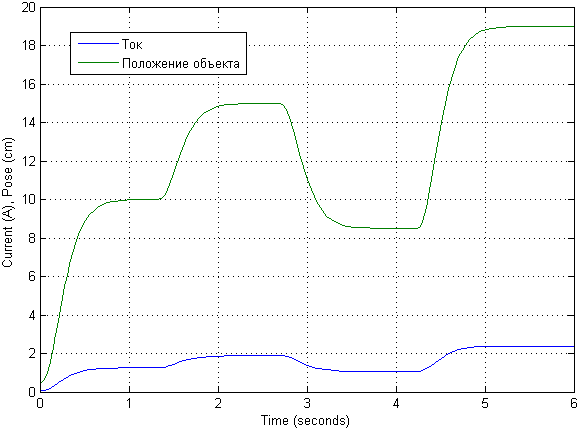
数学模型本身可能看起来有些不同。 它的描述来自数学模型的描述。
结论
磁悬浮系统的这种非线性模型的模态控制根本不适合任何实际需要。 应该考虑该磁悬浮系统的其他实现。
至于单身汉的工作,作者实现了一个关于悬浮的简单装置,以后将对其进行单独描述。