
机器学习中最重要的任务之一是对象检测。 最近,已经发布了一系列基于深度学习的用于对象检测的机器学习算法。 这些算法在实际的计算机视觉应用(尤其是当前非常流行的无人驾驶汽车)中占据着中心位置之一。 但是所有这些方法都是老师的教学方法,即 他们需要一个巨大的数据集(巨大的数据集)。 自然地,需要一种能够从“原始”(未分配)数据中学习的模型。 我试图分析现有方法,并指出其开发的可能方法。 我问所有希望在凯特下怜悯的人,这会很有趣。
问题的现状
自然地,这个问题的提法已经存在了很长时间(几乎是从机器学习存在的头几天开始),并且有足够数量的关于该主题的著作。 例如,我最喜欢的
带卷积神经网络的空间不变无监督对象检测之一 。 简而言之,作者正在训练可变自动编码器(VAE),但是这种方法对我提出了许多问题。
一点哲学
那么,图像中的对象是什么? 要回答这个问题,我们必须回答这个问题-为什么我们甚至将世界分成对象? 在对这个问题进行了一点思考之后,我对这个问题只有一个答案(我并不是说没有其他人,我只是没有找到他们)-我们正在努力寻找一种易于理解和控制描述世界所需信息量的世界表示形式在当前任务的范围内。 例如,对于图像分类任务(通常是错误地制定的-很少有一个对象的图像。即,我们解决的不是图像中显示的问题,而是哪个对象是“主要”问题),我们只需要说图像是“汽车”即可反过来,对于检测对象的任务,我们想知道那里有哪些“有趣”的对象(我们对图片中树木中的所有叶子都不感兴趣),以及它们在哪里,对于描述场景的任务,我们想要获得“有趣”过程的名称 它在那里发生,例如“日落”等。
事实证明,对象是数据的便捷表示形式。 此表示应具有哪些属性? 视图应包含有关图像的尽可能完整的信息。 即 有了对象描述,我们希望能够以必要的准确度还原原始图像。
如何用数学表达? 想象一下,图像是随机变量X的实现,而表示形式将是随机变量Y的实现。鉴于上述,我们希望Y包含尽可能多的有关X的信息。自然地,为此,请使用互信息的概念。
机器学习模型可提供最大信息
可以将对象的检测视为生成模型,该模型在输入处接收图像
,并且输出是图像的对象表示
。

现在让我们回想一下计算互信息的公式:
在哪里
关节密度分布
被边缘化。
在这里,我不会深入探讨为什么这个公式看起来像这样,但是我们将在内部相信它是非常合逻辑的。 顺便说一句,基于所描述的考虑,没有必要选择确切的互信息,它可以是任何其他“信息”,但是我们将在接近结尾时再谈谈。
特别细心的人(或阅读过信息论书籍的人)已经注意到,共同信息不过是联合分配与边际分配之间的库尔贝克-莱伯勒差异。 这里会产生一些复杂的问题-至少阅读过两本有关机器学习的书籍的人都知道,如果我们仅从两个分布中获得样本(即我们不知道分布函数),那么它甚至没有进行优化,而是评估了Kullback的差异, Leibler的任务非常艰巨。 此外,正是由于这个原因,我们钟爱的GAN诞生了。
幸运的是,使用“
互信息的变化边界”中所述的使用较低的变化边界的奇妙想法对我们有所帮助。 相互信息可以表示为:
或
在哪里
-给定图像的表示形式的分布,由我们的神经网络参数化并可以从该分布进行采样,但是我们不需要能够评估特定样本的密度或概率(这通常是许多生成模型的典型特征)。
是由第二个神经网络参数化的某个密度函数(在大多数情况下,我们需要2个神经网络,尽管在某些情况下它们可以由第一个神经网络表示),这里我们必须能够计算所得样本的概率。
价值
称为下变异边界。
现在我们可以解决问题的方法,即不增加互信息本身,而是增加其较低的变化边界。 如果分配
如果选择正确,则在变分边界的最大值处,相互信息将重合,但在实际情况下(当分布
无法想象
,但包含相当大的功能系列)将非常接近,这也适合我们。
如果有人不知道它是如何工作的,我建议您仔细考虑EM算法。 这是一个完全相似的情况。
这是怎么回事 实际上,我们获得了训练自动编码器的功能。 如果Y是神经网络的输出结果,而输入则包含一些图片,则意味着
在哪里
神经网络转换功能。 并通过高斯近似逆分布,即
我们得到:
这是自动编码器的经典功能。
自动编码器还不够
我认为许多人已经想训练自动编码器,并希望在其隐藏层中会有对特定对象做出反应的神经元。 通常,可以确认类似的东西,并且可以
使用大规模无监督学习构建高级功能 。 但这仍然是完全不切实际的。 最细心的人已经注意到,本文的作者使用了正则化-他们添加了一个在隐藏层中提供稀疏性的术语,并且用黑色和白色写道,没有这个术语,就不会发生任何事情。
最大限度地利用相互信息的原理足以学习“便捷”的想法吗? 显然不是,因为我们可以选择等于X的Y(即使用图像本身作为表示)或任何双射变换,所以在这种情况下互信息达到无穷大。 这个价值已经没有了,但是我们知道这是一个非常糟糕的主意。
对于展示的“便利性”,我们需要一个附加标准。 以上文章的作者将稀疏性视为“便利”。 这是对图片中应该有一些“重要对象”的假设的一种实现。 但是我们将走得更远-我们不仅要了解这样的事实,还想知道它在哪里,重叠了多少等等。 问题是,如何使神经网络解释神经元的输出,例如对象的坐标? 答案很明显-该神经元的输出应精确地用于此。 也就是说,知道了这个主意之后,我们必须能够生成与原始图片“相似”的图片。
总体思路是从Facebook的员工那里借来的。
编码器将如下所示:

在哪里
-描述对象的一些向量,
-对象的坐标,
-对象的比例,
-物体在深处的位置,
-对象存在的概率。
也就是说,输入神经网络接收一个预定大小的图片,我们要在该图片上找到对象并发出一系列描述。 如果我们想要单通网络,那么不幸的是,此阵列必须固定大小。 如果我们想找到所有对象,那么我们将不得不使用招聘网络。
解码器将如下所示:
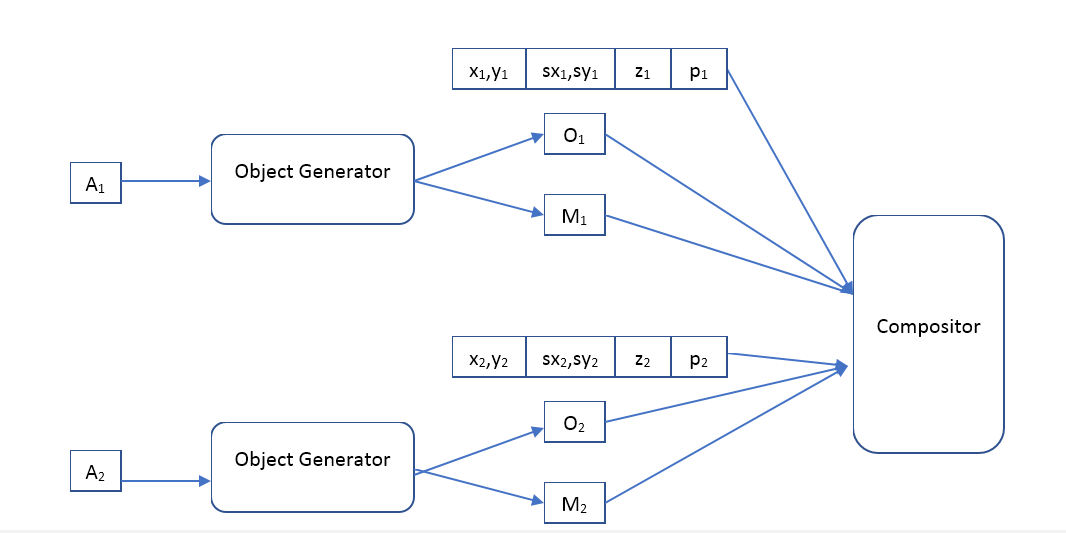
其中对象生成器是一个在输入端接收对象描述向量并给出
-对象的图像(一定标准尺寸)和不透明像素的蒙版(不透明蒙版)。
合成器-接收所有对象,蒙版,位置,比例,深度的输入图像,并形成输出图像,该图像应与原始图像相似。
我们的方法和VAE有什么区别?
似乎我们想使用一种自动编码器,其结构与文章中
使用卷积神经网络的空间不变无监督对象检测的作者相同,所以问题是有什么区别。 那里和那里的自动编码器,仅在第二个版本中是可变的。
从理论上讲,差异非常大。 VAE是一个生成模型,其任务是使两个分布(初始图片和生成的图片)尽可能相似。 一般而言,VAE不保证从原始图像生成的对象的“描述”生成的图像至少与原始图像稍有相似。 顺便说一下,VAE
自动编码变体贝叶斯的作者自己也谈到了这一点。 那么为什么它仍然起作用? 我认为神经网络和“描述”的选定架构有助于增加图像和“描述”的相互信息,但是我找不到该假设的任何数学证据。 给读者一个问题,有人能解释作者的结果吗?他们还原的图像与原始图像非常相似,为什么?
此外,使用VAE会迫使作者指定“描述”的分布,并且最大化互信息的方法对此不做任何假设。 这给了我们额外的自由度,例如,我们可以尝试将向量聚类在已经训练好的模型上
描述和外观-也许这样的系统将学习对象的类别? 应当指出,使用VAE进行此类聚类没有任何意义,例如,本文的作者对这些向量使用了高斯分布。
实验
不幸的是,现在该工作需要大量时间,并且不可能在可接受的时间内完成它。 如果有人想编写几千行代码,训练数百种机器学习模型并进行许多有趣的实验,仅仅是因为它给他(或她)带来了乐趣-我将很高兴携手并进。 写个人。
这里的实验领域非常广泛。 我计划从训练经典的自动编码器(将图像确定性地映射到描述和高斯逆分布)开始,然后看看它能学到什么。 在最初的实验中,使用Facebook上的家伙所描述的作曲家就足够了,但是在将来,我认为与各种作曲家一起玩将非常有趣,并且有可能使他们也变得可学。 比较不同的正则器:没有它,稀疏等。 比较前馈和递归模型的使用。 然后使用更高级的分布模型进行逆分布,例如,
使用Real NVP进行
密度估算 。 看看使用更灵活的模型会带来多少好坏。 看看如果描述中的图像显示不确定(从某些条件分布生成),将会发生什么。 最后,尝试将各种聚类方法应用于描述向量
并了解这种系统是否可以学习对象类。
但最重要的是,我真的想比较基于最大化互信息的模型的质量和带有VAE的模型。