经济学的黄金分割率-这是什么？

关于传统意义上的“黄金分割”的几句话

据信，如果将分段划分成较小的部分将与较大的部分（如较大的部分）相关联到整个分段，则这样的划分将得出1 / 1,618的比例，古希腊人从更古老的埃及人那里借来，称为“黄金比例。” 从埃及金字塔到勒·柯布西耶（Le Corbusier）的理论建筑，许多建筑结构-建筑物轮廓之间的关系，关键要素之间的关系-就是基于这个比例。
她还对应于斐波那契数，斐波那契数的螺旋给出了该比例的详细几何图示。

而且，人体的大小（从脚掌到肚脐，从肚脐到头部，从头到举手的手指），从中世纪（维特鲁威人等）所见的理想比例开始，以人体学测量的苏联人口结尾，仍然接近这个比例。

而且，如果我们加上这样的数字是在完全不同的生物物体中发现的：软体动物的壳，向日葵和雪松球果中的种子排列，那么很清楚为什么将一个非理性的数字（从1,618开始）宣布为“神”-其踪迹甚至以星系的形式被追踪到斐波那契螺旋式上升！

给出以上所有示例，我们可以假设：

1. 我们正在处理真正的“大数据”，
2. 即使作为一个初步的近似值，它们也指向“黄金分割”的某个确定的，甚至不是普遍性的分布，而且其分布异常接近。

在经济学中

众所周知且使用率很高的洛伦兹图使人口收入可视化。 这些功能强大的宏观经济工具具有各种变化和细化（十分位数系数，基尼系数），可用于统计数据，以对国家及其特征进行社会经济比较，并且可以为在税收，医疗保健，国家发展计划制定和发展等领域做出大型政治和预算决策的理由。地区。

而且，尽管收入和支出在日常生活中紧密相关，但在Google中并非如此……这太了不起了，但是我设法找到了Lorentz图和支出分配之间的联系，仅涉及两位俄罗斯作者（如果有人知道这样的著作，我将不胜感激。互联网的俄语和英语地区）。

首先是T. M. Bueva的论文。 论文特别致力于Mari禽场的成本优化。

另一位作家V.V. Matokhin（提供了作者的相互联系）可以更大规模地解决此问题。 Matokhin是小学教育的物理学家，致力于管理决策中使用的数据的统计处理以及评估公司的适应性和可管理性。

下面给出的概念和示例摘自V.Matokhin及其同事（Matokhin，1995），（Antoniou等，2002），（Kryanev等，1998），（Matokhin等，2018）的著作。 在这方面，应该补充的是，在解释其作品时可能出现的错误是这些著作的作者的专有财产，不能归因于原始的学术著作。

意外的恒定性

反映在下图中。

1.在“高温超导”国家方案下分配用于科学技术竞赛的赠款。 （Matokhin，1995年）

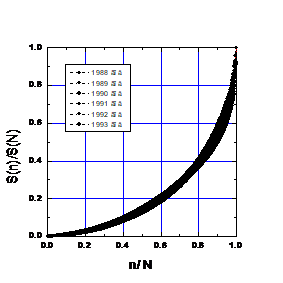图1。 1988-1994年项目年度资金分配比例。
年度分配的主要特征在表3中给出，其中SN是年度拨款额（百万卢布），N是资助项目数。 考虑到比赛陪审团的组成，比赛预算，甚至金钱规模（1991年改革之前和之后）多年来发生了变化，因此实时曲线的稳定性是惊人的。 图上的黑条由实验点组成。

表3

2.与库存销售有关的成本曲线（Kotlyar，1989年）

图2

3.下巴工资表

例如，为了构建该图，我们从“声明：应该假定每年普通年薪所在州的职级有多少”文件中获取数据（Suvorov，2014年）（“胜利的科学”）。


4.美国中层经理的平均工作时间表（Mintzberg，1973年）

图4

给出的归一化图表表明，它们所说明的经济活动具有一般模式。 由于经济活动的具体细节，地点和时间存在根本性差异，因此日程安排的相似性很可能是由经济体系运作的一些基本条件所决定的。 在进行数以千计的经济活动的过程中，基于大量的反复试验，该活动的主题已寻求最佳的资源分配策略。 并在当前活动中直观地使用它。 这个假设与众所周知的帕累托原理非常吻合：我们20％的努力产生了80％的结果。 在这里可以清楚地看到类似的东西。 给定的曲线图表示经验规律性，当指数“ alpha”等于2时，将以足够的精度描述经验规律性。在此指标中，洛伦兹图变为圆的一部分。

您可以称呼此名称（尚无稳定的名称特征）生存。 与野外生存类似，经济系统的生存取决于其对社会经济环境条件的适应性以及适应市场条件变化的能力。

这意味着支出分配接近理想的系统（α的度数等于2，或者“在圆周上”支出分配）具有保持其现有形式的最大机会。 值得注意的是，在某些情况下，这种分配决定了企业的最大盈利能力。 例如，这里。 偏离理想值的系数越小，企业的盈利能力就越高（Bueva，2002）。

表（片段）

实际发现

在计划公司和家庭的支出时，从它们构建洛伦兹曲线并将其与理想的曲线进行比较很有用。 您的图表越接近理想状态，就越有可能正确地计划并且您的活动将成功。 如此亲密的关系证实了您的计划与人类的经济活动经验相吻合，并存于诸如帕累托原理这样的普遍公认的经验法则中。

但是，我们可以假设，在这里我们所谈论的是关注利润率的成熟经济系统的功能。 如果我们不是在谈论最大化利润，而是在谈论公司现代化的任务或从根本上增加其市场份额，那么您的成本分布曲线将偏离圈子。

显然，在具有特定经济的初创企业的情况下，与最高成功概率相对应的洛伦兹图也将偏离圆圈。 可以假设，圆内费用分布曲线的偏差既对应于风险的增加，又对应于公司适应性的降低。 但是，如果不依赖于大型的统计数据集（无论成功与否），就很难进行合理的合格预测。

根据另一个假设，成本分布曲线从圆到外的偏差可能是控制过度的信号，也可能是即将破产的信号。 为了检验这一假设，还需要一定的参考基础，就像初创企业一样，该参考基础不太可能存在于公共领域。

而不是结论

关于该主题的第一批大型出版物的历史可以追溯到1995年（Matokhin，1995年）。 这些作品鲜为人知，其普遍性以及经济学家广泛使用的模型和工具的全新应用，在某种意义上仍然是个谜...