数学家已经证明，将随机过程应用于随机表面总是会产生某些模式
在原始文章中，这是一个可以扭曲的三维图像在有关寻找失落的方舟的
影片中 ，印第安纳·琼斯不得不寻找一个秘密房间，藏着传说
中的《约柜》 。 为了确定其确切位置，印第安纳州需要找到一张特殊的地图，该地图只有在一天中的特定时间太阳在特定房间的特殊晶体中发光时才可见。
在许多神话中都发现了类似的想法，即只有在某些特定情况下，才可以披露最重要的信息。 它发生在数学中，有时发生在意外情况下。 现在，
三位数学家已经证明 ，如果对某种类型的随机性进行非常精确的调整，那么就会出现复杂的几何图形-就像一张在普通地板上有宝藏的地图。
这些棋子就像散布在网格上的象棋棋子，而棋子本身又是由随机过程创建的。 有人会认为，将随机性堆积为随机性会引起混乱。 事实证明，就像雪花一样，当每个雪花都是唯一的，但同时又都是雪花时，如果只有条件完全符合需要，乱七八糟的东西会收敛为通用形式。
转折点
人人都知道数学家学习形式。 其中大多数形式都遵循确定性规则：如果我向您提供构建球体的说明，您每次都会收到相同的球体。
但是，即使是数学家，也会研究由于随机过程（例如，
随机游走）而获得的形式，即
随机行走的路径，其每一步的方向都是随机选择的。 除了随机游走外，还有其他类型的随机几何对象，例如，随机的二维表面（想象一个山丘和山谷随机散布的风景）和随机的地图（由线连接的一组随机点）。
通过粘贴三角形获得的随机表面所有这些形式互不相同。 但是，数学家发现这些随机过程收敛到某些规范形式。 例如，所有随机行走都是
布朗运动的一种形式，具有较长的行走。 近年来，数学家发现了规范形式和其他随机过程-并为此赢得了各自领域的最高奖项。
新证据与对另一个随机过程的基本属性的理解有关。
首先创建一个随机曲面。 首先，您需要将三角形粘合在一起。 然后，它们需要以任何方式匹配在一起，只是为了使生成的表格闭合，就像礼物上的包装（没有孔）一样。 如果您手上有一定数量的三角形，您将有很多机会。 其中一些“三角剖分”将产生接近光滑的表面，看起来像一个球。 它们中的大多数看起来会更粗糙-像山脉一样的极端表面。
该著作的合著者，布兰代斯大学的数学家
奥利维尔·伯纳迪说：“它看起来不会像常规球体那样大，它的峰值会很大。”里昂
奥利维尔·伯纳迪（Olivier Bernardi），尼古拉斯·库里安（Nicholas Curien）和格雷戈里·迈尔蒙特（Gregory Myermont）Myermont和另一位数学家
Jean-Francois le Gall在以前的工作中建立了这些随机三角剖分的许多性质。 通过在随机三角剖分的基础上增加第二层随机性，新的证明更加进一步。
要添加新的随机性，请标记三角形在拐角处相遇的每个点-数学家称之为顶点。 用黑色或白色随机给顶点着色。 您可以通过扔硬币来做到这一点，尽管该硬币可能并不完全诚实，而且其重量超过一侧。
绘制峰后，您可以询问有关创建的图案的各种问题。 基本原理之一：仅使用一个黑色顶点就能沿着表面走多远？ 沿着相同颜色的连接顶点移动的过程称为渗透。 这是研究与流体通过多孔介质同名的物理现象的数学方法。
根据硬币重量的分配方式，很容易渗透（或不渗透）：如果硬币倾向于散发出黑色顶点，几乎可以保证渗透。 如果要引渡白人，几乎肯定不会渗入。
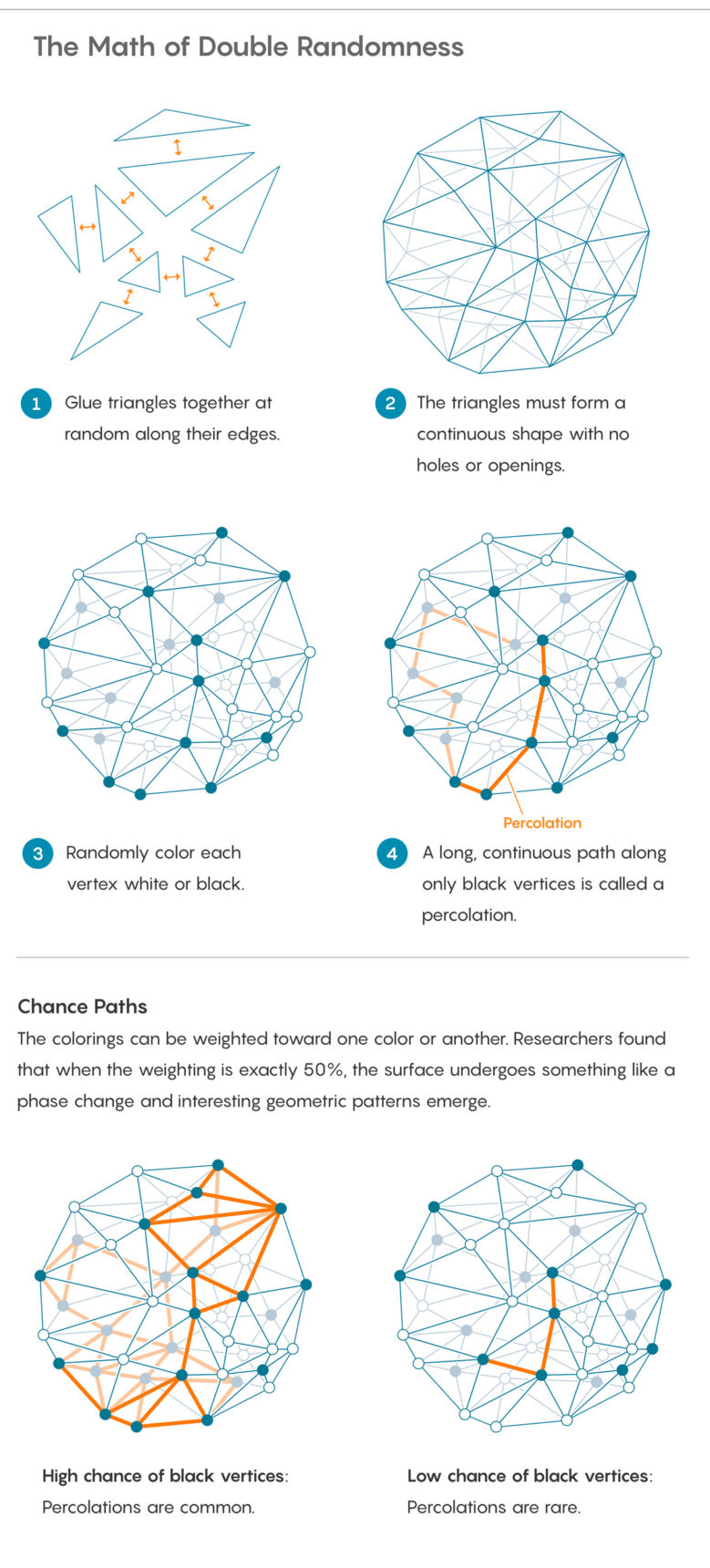
Bernardi，Curien和Myermont研究了介于这些极端之间的案例，这是硬币重量变化的转折点，此时泄漏从几乎不可能变为几乎可以保证的现象。 他们称此为“关键阈值”。 这是一个相变的例子，这是热水突然变成蒸汽的神奇时刻。
Curien说：“关键阈值意味着，如果我稍微改变参数，则系统的行为将从戏剧性变为具有不同符号的戏剧性。”
物理学家对相变很感兴趣，因为许多最重要的自然现象就在边缘发生。 数学家对相变也很感兴趣，因为重要的数学性质经常出现在这些点上。
麻省理工学院的数学家
斯科特·谢菲尔德 （
Scott Sheffield）说：“我们知道水会在100度沸腾，从而形成所有这些疯狂的模式和蒸汽形式。” 有时候，这种疯狂和野蛮的行为变得非常有趣。 这个阶段的过渡要求我们理解它。”
在新工作中，三位数学家证明这种疯狂的行为正好在泄漏的相变中表现出来。 他们表明，在此临界阈值下，出现了一种几何形式-独特，同时又通用。
隐藏的机会
工作的第一部分确定如何校正硬币，以使顶点的颜色落在存在和不存在渗透之间的阈值上。 凭直觉，他们证明了理想的硬币是关键值-使50％的机会掉黑，而50％的机会掉白。
“这是工作的第一部分。 伯纳迪说：“我们证明，恰好一半发生了一些有趣的事情。”
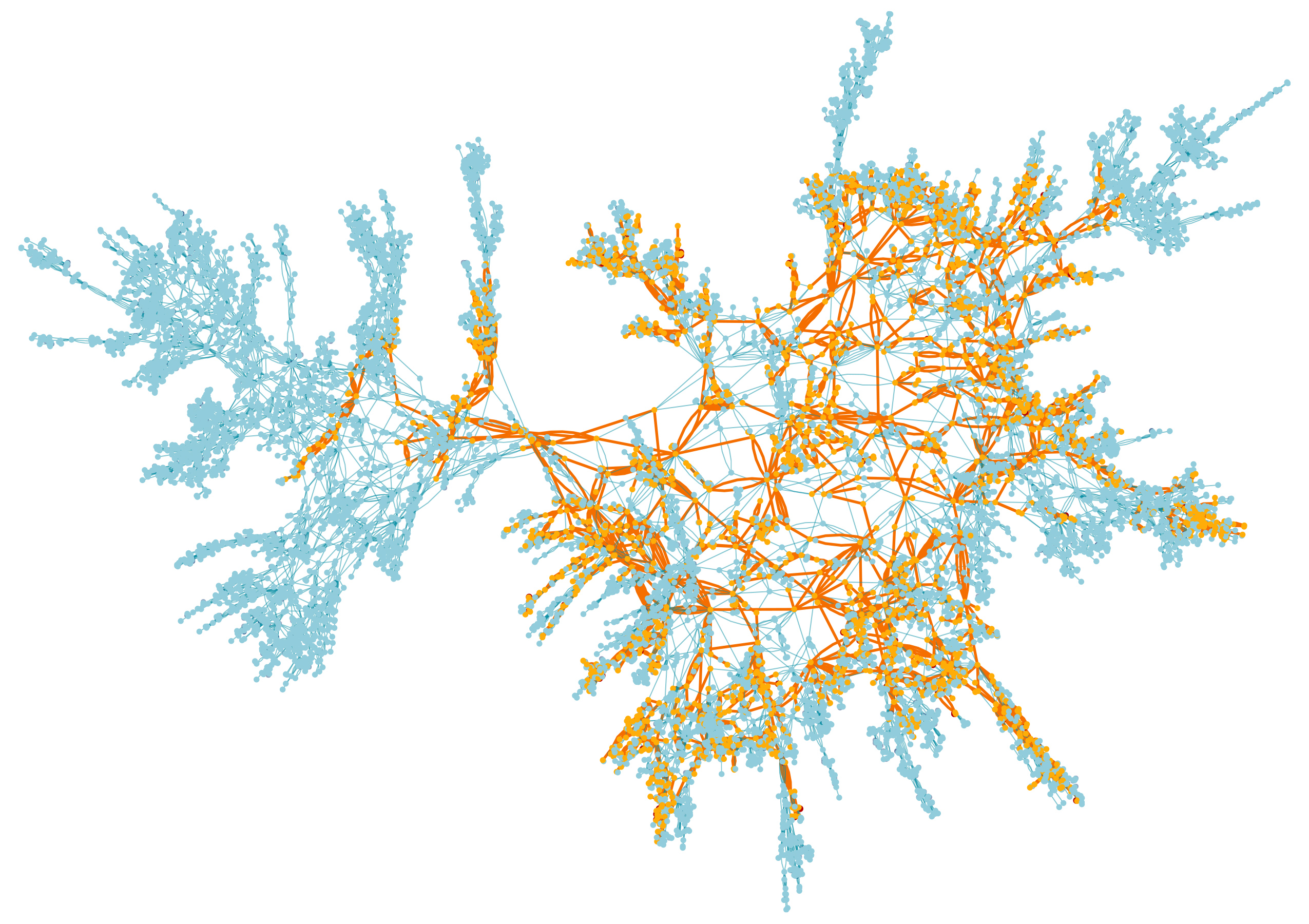随机表面的峰图，最大的簇用橙色标记在第二部分中，我们研究那里发生的事情。 用公平的硬币为黑色和白色顶点着色，可以在黑色和白色顶点簇之间获得良好的平衡。 簇簇彼此围绕生长，就像杂草丛争夺一个杂草丛生的花园中的一个地方一样，创造出复杂的几何形状，当其中一朵花在山峰之中占主导地位时，它们就不会出现。
谢菲尔德说：“通过选择一个关键参数，您会发现大型集群。” “但是，它们不会弄脏整个东西，而且它们也不小。”
由于曲面是随机创建的，并且顶点着色的过程也是随机的，因此一个曲面上的大簇将始终不同于另一曲面上的大簇。 但是数学家已经证明，对于所有表面和所有可能的方式为其顶点着色，最大的簇将具有相同的属性。 他们证明的第一件事是最大的黑色团簇大小在所有表面上的确切概率分布。 他们发现，通常会出现某个中间大小的簇，并且出现更大或更小的簇的频率会随着与该中间点的距离呈指数增长。
他们还认为，所有大型星团都可以简化为相同的规范形式，称为“稳定图”。 稳定图以与布朗运动随机游动相同的方式引用这些聚类。 这意味着，如果各个群集之间的距离略有不同，则群集中的每个随机步在整个图形的几何形状中都不太明显，那么群集将逐渐变为一个共同的形状。 它们看起来像雪花：它们在附近看起来很独特，但它们的共性在远处清晰可见。
“他们发现了这张稳定的地图，这是比例尺的自然极限，”谢菲尔德说。
这项工作扩大了近年来数学家积累的有关随机形式和过程的知识范围。 它也向我们揭示，恰好在随机系统似乎最混乱的那一刻，才开始通过它看到异常的几何顺序。