有两个人叫“范·埃克”。 第一次是在1985年,向世界展示了如何以15美元的价格从监视器(
Van Eck phreaking )拦截数据,第二个是在2010年,提出了一个狡猾的序列(
Van Eck的序列 )。 比这个序列的任务简单得多,只能是它的特性和奥秘。
因此,生成序列成员的算法。 我们以“起始编号”,例如“ 0”,写出来。 下一个术语是在上一个子序列中发生了多少步退缩此数字。 如果从不,则写零。 下一个是在前一个子序列中归零前有多少步,即向后退了一步。 我们写下单位。 单元一-写零。 糟糕,零落了两步。 我们写两个,依此类推...
对于报告点“ 0”,序列的前97个成员:
0、0、1、0、2、0、2、2、1、6、0、5、0、2、6、5、4、0、5、3、0、3、2、9、0, 4,9,3,6,14,0,6,3,5,15,0,5,3,5,2,17,17,0,6,11,0,3,8,0,3,3, 1、42、0、5、15、20、0、4、32、0、3、11、18、0、4、7、0、3、7、3、2、31、0、6、31, 3、6、3、2、8、33、0、9、56、0、3、8、7、19、0、5、37、0、3、8、8、1
图表:
更多时间表:
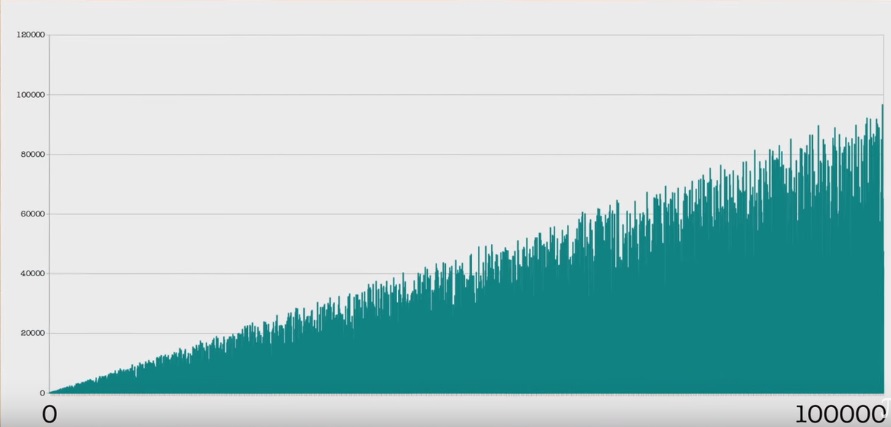
序列的性质很容易证明,其最大项一直在增加,并且具有无限数量的零。 或里面没有句号。 (
这里有一些定理和结果。)
对数图:
Python程式:
A181391 = [0] last_pos = {} for i in range(10**4): new_value = i - last_pos.get(A181391[i], i) A181391.append(new_value) last_pos[A181391[i]] = i
对于起始数字“ 1”,前一百是:
1,0,0,1,3,0,3,2,0,3,3,1,8,0,5,0,2,9,0,3,9,3,2,6,6,0, 6,2,4,0,4,2,4,2,2,1,23,0,8,25,0,3,19,0,3,3,1,11,0,5,34, 0、3、7、0、3、3、1、11、11、1、3、5、13、0、10、0、2、33、0、3、9、50、0、4、42 0、3、7、25、40、0、5、20、0、3、8、48、0、4、15
图表:
对于起始数字“ 2”,前一百是:
2,0,0,1,0,2,5,5,0,3,0,2,5,5,1,10,0,6,0,2,8,0,3,13,0,3, 3、1、13、5、16、0、7、0、2、15、0、3、11、0、3、3、1、15、8、24、0、7、15、5、20, 0、5、3、12、0、4、0、2、24、14、0、4、6、46、0、4、4、1、26、0、5、19、0、3、21, 0、3、3、1、11、42、0、6、20、34、0、4、20、4
图表:
资料来源