用于搜索hh.ru的新提示服务

搜索提示很棒。 我们多久在地址栏中输入完整的站点地址？ 以及在线商店中产品的名称？ 对于此类简短查询，如果搜索提示很好，通常只需输入几个字符即可。 如果您没有二十根手指或难以置信的打字速度，那么您一定会使用它们。
在本文中，我们将讨论我们在上一期《程序员学院》中所做的新hh.ru搜索提示服务。

旧服务有很多问题：

• 他致力于手工选择受欢迎的用户查询；
• 无法适应不断变化的用户偏好；
• 无法对未包含在顶部的查询进行排名；
• 没有纠正错别字。

在新服务中，我们纠正了这些缺陷（同时添加了新缺陷）。

热门查询字典

当根本没有提示时，您可以手动选择用户的前N个查询，并使用单词的确切出现次数（有序或无序）从这些查询中生成提示。 这是一个很好的选择-易于实现，提示准确度高，不会遇到性能问题。 长期以来，我们的总结工作都是这样，但是这种方法的一个主要缺点是发行的完整性不足。

例如，请求“ javascript开发人员”没有进入这样的列表，因此当我们输入“ javascript时间”时，没有任何内容可显示。 如果我们仅考虑最后一个单词来补充请求，那么我们将首先看到“ javascript杂工”。 出于同样的原因，通过达默劳-莱文施泰因距离找到最接近的单词，将不可能比标准方法更困难地进行纠错。

语言模型

另一种方法是学习评估查询的概率并为用户查询生成最可能的延续。 为此，请使用语言模型-一组单词序列的概率分布。



由于用户请求通常都很短，因此我们甚至没有尝试使用神经网络语言模型，而是将自己限于n-gram：

$$

$$P（w_1 \点w_m）= \ prod_ {i = 1} ^ mP（w_i | w_1 \点w_ {i-1}）\大约\ prod_ {i = 1} ^ mP（w_i | w_ {i-（ n-1）} \点w_ {i-1}）$$

作为最简单的模型，我们可以采用概率的统计定义，然后

$$

$$P（w_i | w_1 \点w_ {i-1}）= \ frac {count（w_1 \点w_i）} {count（w_1 \点w_ {i-1}）}$$

但是，这样的模型不适合评估示例中未包含的查询：如果我们未观察到“初级开发人员java”，那么结果是

$$

$$P（\文本{初级开发者Java}} = \ frac {count（\文本初级开发者Java}}} {count（\文本{初级开发者Java}}} = 0$$

要解决此问题，可以使用各种平滑和插值模型。 我们使用Backoff：

$$

$$P_ {bo}（w_n | w_1 \点w_ {n-1}）= \开始{cases} {P}（w_n | w_1 \点w_ {n-1}），计数（w_1 \点w_ {n- 1}）> 0 \\ \ alpha {P_ {bo}}（w_n | w_2 \点w_ {n-1}），计数（w_1 \点w_ {n-1}）= 0 \结束{cases}$$

$$

$$\ alpha = \ frac {P（w_1 \点w_ {n-1}）} {1-\ sum_wP_ {bo}（w | w_2 \点w_ {n-1}）}$$

其中P是平滑概率 $$$w_1 ... w_ {n-1}$ （我们使用了拉普拉斯平滑）：

$$

$$P（w_n | w_1 \点w_ {n-1}）= \ frac {count（w_n）+ \ delta} {count（w_1 \点w_ {n-1}）+ \ delta | V |}$$

其中V是我们的字典。

选项生成

因此，我们能够评估特定请求的可能性，但是如何生成这些相同的请求呢？ 明智的做法是执行以下操作：让用户输入查询 $$$w_1 ... w_n$ ，则可以从条件中找到适合我们的查询

$$

$$w_1 \点w_m = \下陷{w_ {n + 1} \点w_m \ in V} {argmax} P（w_1 \点w_n w_ {n + 1} \点w_m）$$

当然，整理一下 $$$| V | ^ {m-n}，m = 1 \点M$ 无法为每个传入请求选择最佳选项，因此我们将使用Beam Search 。 对于我们的n-gram语言模型，归结为以下算法：

def beam(initial, vocabulary): variants = [initial] for i in range(P): candidates = [] for variant in variants: candidates.extends(generate_candidates(variant, vocabulary)) variants = sorted(candidates)[:N] return candidates def generate_candidates(variant, vocabulary): top_terms = [] #         1, 2, ... n  for n0 in range(n): top_n = sorted(vocabulary, key=lambda c: P(|variant[-n0:]) top_terms.extends(top_n) candidates = [variant + [term] for term in top_terms] #       candidates = sorted(candidates, key=lambda v: P(variant))[:N] return candidates 

这里以绿色突出显示的节点是最终选择的选项，节点前面的数字 $$$w_n$ -概率 $$$P（w_n | w_ {n-1}）$ ，在节点之后- $$$P（w1 ... w_n）$ 。

它变得更好了，但是在generate_candidates中，您需要针对给定的上下文快速获得N个最佳术语。 在仅存储n-gram的概率的情况下，我们需要遍历整个字典，计算所有可能短语的概率，然后对它们进行排序。 显然，这对于在线查询是不可行的。

概率硼

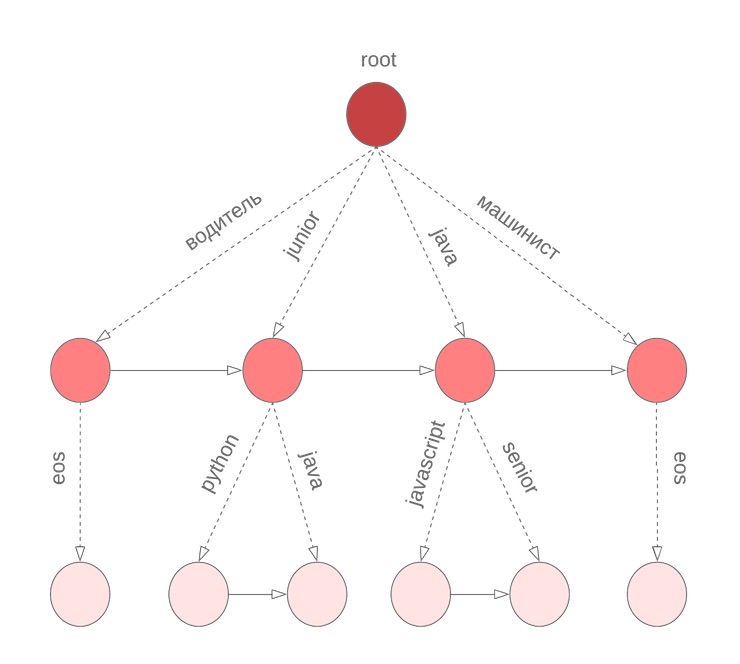
为了快速获得词组连续的条件概率变体中的N个最佳，我们在术语上使用了硼。 在节点中 $$$w_1 \至w_2$ 储存系数 $$$\ alpha$ ，值 $$$P（w_2 | w_1）$ 并按条件概率排序 $$$P（\项目符号| w_1 w_2）$ 条款清单 $$$w_3$ 与 $$$P（w_3 | w_1 w_2）$ 。 特殊术语eos标记短语的结尾。

但是有细微差别

在上述算法中，我们假设查询中的所有单词均已完成。 但是，对于用户现在输入的最后一个单词，情况并非如此。 我们再次需要遍历整个词典以继续输入当前单词。 为了解决这个问题，我们使用了一个符号硼，在它的节点中，我们存储了按单字组概率排序的M个项。 例如，这看起来像我们对于M = 3的java，junior，jupyter，javascript的bor：



然后，在开始进行波束搜索之前，我们找到M个最佳候选词来继续当前单词 $$$w_n$ 并选择N个最佳候选人 $$$P（w_1 \点w_n）$ 。

错别字

好吧，我们已经构建了一项服务，可让您为用户请求提供良好的提示。 我们甚至已经准备好使用新词。 一切都会好起来的。。。 但是用户要小心，不要切换hfcrkflre键盘。

如何解决呢？ 首先想到的是通过找到最接近Damerau-Levenshtein距离的选项来进行校正的搜索，该距离被定义为插入/删除/替换字符或从一行中获得另一个字符所需的两个相邻字符的换位的最小数量。 不幸的是，该距离并未考虑特定更换的可能性。 因此，对于输入的单词“ sapper”，我们可以看到选项“ collector”和“ welder”是等效的，尽管直觉上似乎他们想到了第二个单词。

第二个问题是我们没有考虑发生错误的上下文。 例如，在查询“ order sapper”中，我们仍应首选选项“ collector”而不是“ welder”。

如果您从概率的角度解决错别字的任务，那么很自然地要建立一个嘈杂的渠道模型 ：

1. 字母集 $$$\西格玛$ ;
2. 所有尾随线的集合 $$$\西格玛^ *$ 在他之上
3. 许多行是正确的单词 $$$D \ subseteq \ Sigma ^ *$ ;
4. 给定的分布 $$$P（s | w）$ 在哪里 $$$s \ in \西格玛^ *，w \ in D$ 。

然后，将校正任务设置为为输入s找到正确的单词w。 根据错误的来源，进行测量 $$$P$ 它可以以不同的方式构建，在我们的案例中，明智的方法是尝试估计错别字的可能性（我们称其为基本替换） $$$P_e（t | r）$ ，其中t，r是符号n-gram，然后求和 $$$P（s | w）$ 作为通过最可能的基本替换从w获得s的概率。

让 $$$Part_n（x）$ -将字符串x拆分为n个子字符串（可能为零）。 Brill-Moore模型涉及概率的计算 $$$P（s | w）$ 如下：

$$

$$P（s | w）\大约\ max_ {R \ Part_n（s）} T \ Part_n（s）} \ prod_ {i = 1} ^ {n} P_e（T_i | R_i）$$

但是我们需要找到 $$$P（w | s）$ ：

$$

$$P（w | s）= \ frac {P（s | w）P（w）} {P（s）} = const \ cdot P（s | w）\ cdot P（w）$$

通过学习评估P（w | s），我们还将解决在相同的Damerau-Levenshtein距离下对选项进行排名的问题，并且可以在校正错字时考虑上下文。

计算方式 $$$P_e（T_i | R_i）$

为了计算基本替换的概率，用户查询将再次为我们提供帮助：我们将组成单词对（s，w），其中

1. 在达默劳-莱文施泰因关闭；
2. 其中一个词比其他N词更常见。

对于此类对，我们根据Levenshtein考虑最佳比对：


我们组成s和w的所有可能分区（我们将长度限制为n = 2、3）：n→n，pr→rn，pro→rn，ro→po，m→``，mm→m等。 对于每个n-gram，我们发现

$$

$$P_e（t | r）= \ frac {count（r \ to t）} {count（r）}$$

计算方式 $$$P（s | w）$

计算方式 $$$P（s | w）$ 直接拿 $$$O（2 ^ {| w | + | s |}）$ ：我们需要对w的所有可能分区与s的所有可能分区进行排序。 但是，前缀上的动态可以给出以下答案： $$$O（| w | * | s | * n ^ 2）$ 其中n是基本替换的最大长度：

$$

$$d [i，j] = \开始{cases} d [0，j] = 0＆j> = k \\ d [i，0] = 0＆i> = k \\ d [0，j] = P（s [0：j] \ space | \ space w [0]）＆j <k \\ d [i，0] = P（s [0] \ space | \ space w [0：i]）＆ i <k \\ d [i，j] = \下陷{k，l \ le n，k \ lt i，l \ lt j} {max}（P（s [jl：j] \ space | \ space w [ik：i]）\ cdot d [ik-1，jl-1]）\ end {cases}$$

在此，P是k元语法模型中相应行的概率。 如果仔细观察，它与采用Ukkonen裁剪的Wagner-Fisher算法非常相似。 在每一步我们都得到 $$$P（w [0：i] | s [0：j]）$ 通过列举所有修复程序 $$$w [i-k：i]$ 在 $$$s [j-l：j]$ 服从 $$$k，l \ le n$ 以及最可能的选择。

回到 $$$P（w | s）$

因此，我们可以计算 $$$P（s | w）$ 。 现在我们需要选择几个最大化的选项 $$$P（w | s）$ 。 更确切地说，对于原始请求 $$$s_1s_2 \点s_n$ 你必须选择 $$$w_1 \点w_n$ 在哪里 $$$P（w_1 \点w_n | s_1 \点s_n）$ 最大。 不幸的是，诚实地选择方案不符合我们的响应时间要求（项目截止日期临近），因此我们决定重点关注以下方法：

1. 从原始查询中，我们可以通过更改k个最后一个单词来获得几个选项：
   
   1. 如果产生的术语的概率比原始术语高出几倍，我们将更正键盘布局；
   2. 我们发现单词Damerau-Levenshtein距离不超过d的单词；
   3. 从中选择前N个选项 $$$P（s | w）$ ;
2. 将BeamSearch与原始请求一起发送到输入；
3. 在对结果进行排名时，我们对获得的选项进行折现 $$$\ prod_ {i = 0} ^ {k-1} P（s_ {n-i} | w_ {n-i}）$ 。

对于条款1.2，我们在前向和反向前缀树中基于模糊搜索使用了FB-Trie算法（正向和反向trie）。 事实证明，这比评估整个字典中的P（s | w）更快。

查询统计

通过语言模型的构建，一切都变得很简单：我们收集有关用户查询的统计信息（我们请求了给定短语多少次，有多少用户，有多少注册用户），我们将请求分成n-gram并构建了burs。 错误模型更加复杂：至少需要一个正确的单词的词典来构建它。 如上所述，为了选择训练对，我们使用了这样的假设：这些训练对在Damerau-Levenshtein距离上应该很近，并且应该比其他训练次数频繁出现几次。

但是数据仍然太嘈杂：xss注入尝试，错误的布局，剪贴板中的随机文本，经验丰富的用户（请求“程序员c而不是1c”）， 来自通过键盘的猫的请求 。


因此，为了清除源数据，我们排除了：

• 低频术语；
• 包含查询语言运算符
• 淫秽词汇。

他们还纠正了键盘的布局，检查了空缺和开放词典中的单词。 当然，不可能解决所有问题，但通常这些选项要么完全被切断，要么位于列表的底部。

在生产中

就在项目保护之前，他们在生产中为内部测试启动了一项服务，几天后-为20％的用户提供了服务。 在hh.ru中，所有对用户而言重要的更改都将通过AB测试系统进行 ，这不仅使我们能够确定更改的重要性和质量，而且还能发现错误 。



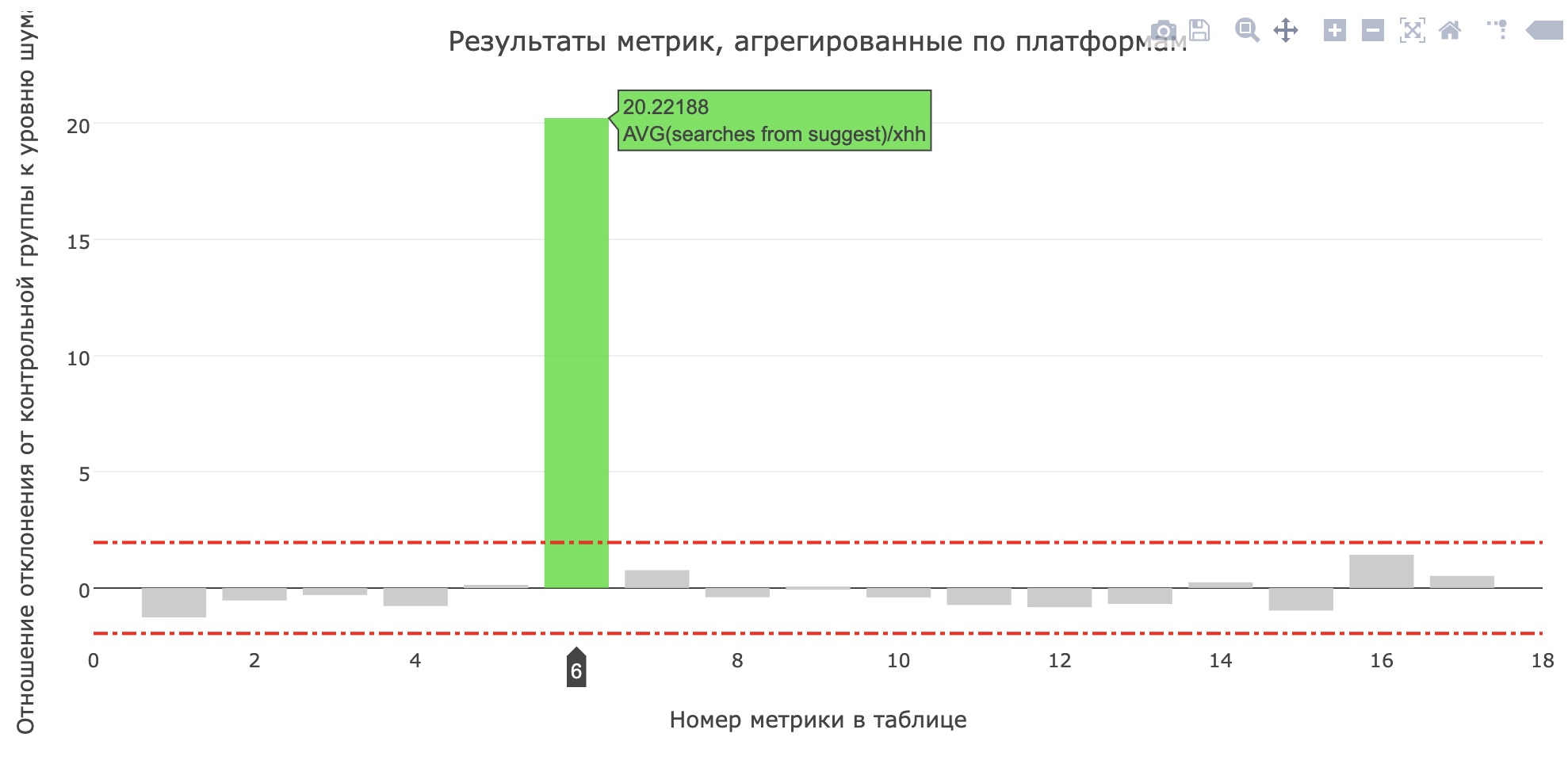
申请人的最接近的平均搜索次数的指标有所提高（从0.959增加到1.1355），最接近的所有搜索查询的份额从12.78％增加到15.04％。 不幸的是，主要产品指标并没有增长，但是用户肯定开始使用更多技巧。

最后

关于学院的流程，其他经过测试的模型，我们为模型比较编写的工具以及在会议上我们决定开发哪些功能以赶上中间演示的故事，这些都没有余地。 查看过去学校的记录，在https://school.hh.ru上请求，完成有趣的任务并开始学习。 顺便说一下，检查任务的服务也是由前一组的毕业生完成的。

读什么？

1. 语言模型导论
2. 布里摩尔模型
3. 三氟甲烷
4. 您的搜索查询会怎样