可视化大图，最小图

如果您需要绘制图形，但手臂下面的工具却会花些力气甚至吞噬所有RAM并挂断系统，该怎么办？ 在过去的几年中，使用大型图（数亿个顶点和边）时，我尝试了许多工具和方法，但几乎没有找到不错的评论。 因此，现在我自己写一篇这样的评论。

为什么要完全可视化图形？

找到要寻找的东西

在输入处，我们通常只有一组顶点和边，这实际上是一个图。 我们可以计算一些统计特征，并根据统计特征绘制图形，但这并不能清楚地说明其含义。 良好的可视化效果可以显示出集群是否具有桥或桥，或者该集群是同质的，还是可能融合成一个块到某个主要吸引中心。

自夸

根据定义，数据可视化解决了表示问题。 如果已经完成一些工作，那么您可以在壮观的图片中显示结论。 例如，如果您对图进行了聚类，则可以为聚类中的图着色，并显示不同标签之间的相互关系。

取得迹象

尽管事实上图形可视化算法主要只是作为获取图像的工具开发的，但它们仍可以用作缩小尺寸的方法。 如果图形本身由邻接矩阵表示，则它是高维空间中的数据，并且在渲染时，我们为每个顶点获得两个坐标（有时为三个或更多，但这是一个例外）。 可视化中顶点的接近度通常表示属性的相似性。

大图有什么问题？

大图是指尺寸，例如，从一万个顶点或边开始。 对于较小的尺寸，通常没有问题，因为通过Internet进行快速搜索可以找到的几乎所有工具基本上都可以很好地解决此类问题。 大图怎么了？ 两个问题：这是可读性和速度。 预期对象越多，导航它们的难度就越大。 对于大型图形，通常会获得无法理解的图片。 另外，图算法通常非常慢，许多算法的复杂度与顶点和/或边的数量的平方（有时是立方体）成比例。 即使您等待渲染，仍然无法承受许多选择来获得满意的结果。

不同的聪明人对此有何看法？

我想引起注意的几件作品：
[1] Helen Gibson，Joe Faith和Paul Vickers：“用于信息可视化的二维图形布局技术的调查”
他们首先整理出绘制图形的方法，解释工作原理，然后尝试全部尝试。 有一个非常详细的表，其中包含有关不同算法的信息，包括算法的复杂性。

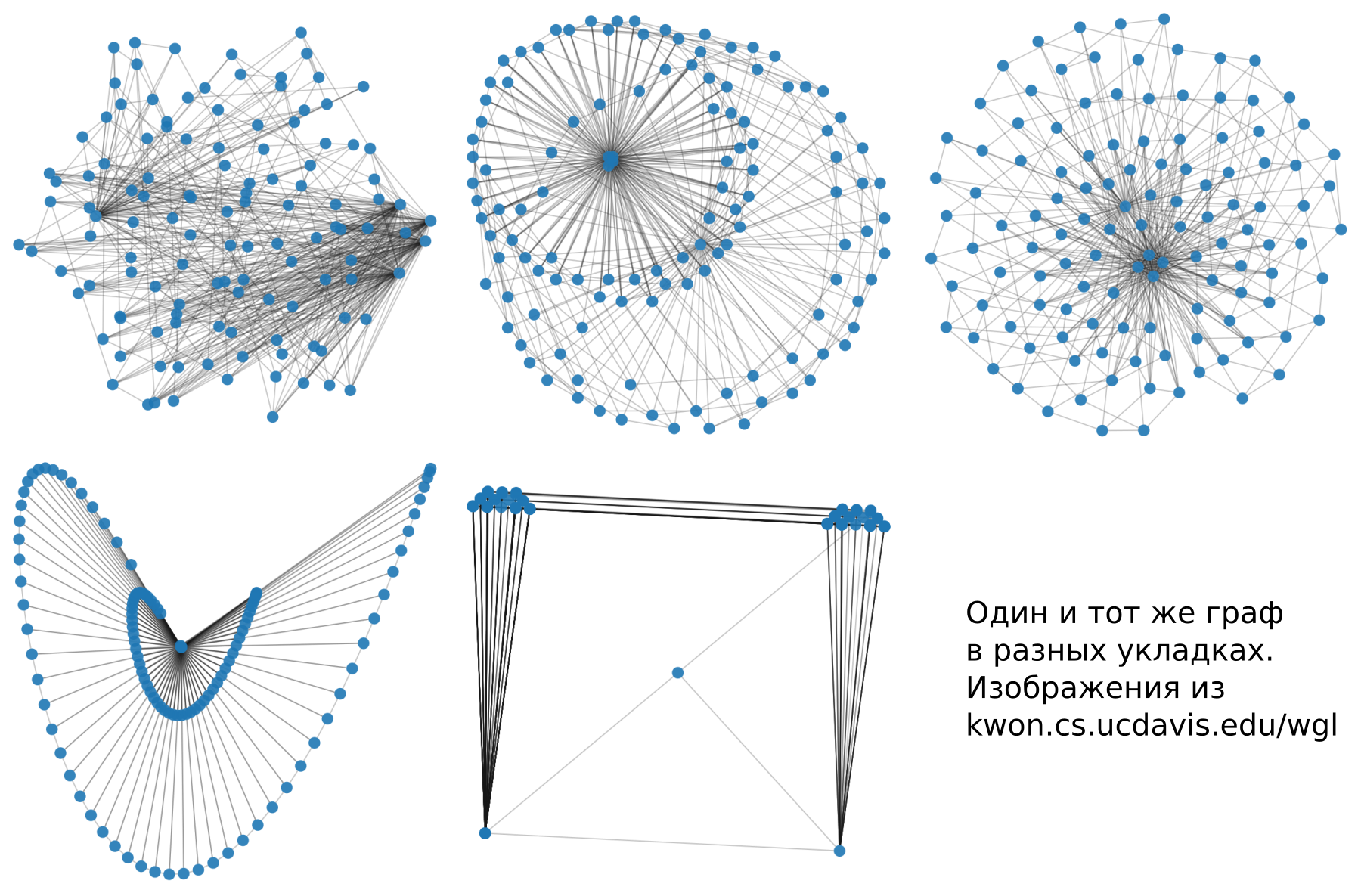
[2]权贤H，塔里克·克里诺弗沙宁和马关流“在这种布局中图将是什么样？ 大型图可视化的机器学习方法”

在这里，我们的同志们变得非常困惑，并获得了他们所能实现的图形可视化算法的所有实现。 然后他们可视化了许多图形并提供了标记标记。 根据结果​​，我们教了模型以评估图形在不同样式选项中的外观。 我从本文拍了一些照片。

理论

堆叠是一种将坐标映射到图形的每个顶点的方法。 通常来说，我们谈论的是平面上的坐标，尽管通常来说不必一定是平面。 几乎不需要简单地使用两个以上的尺寸。

什么是好的造型？

说起来好坏很容易，但是很难向机器解释如何进行这样的评估。 为了获得良好的样式，通常会优化所谓的“美学”指标，这些指标应更加客观地制定。 以下是其中一些：

最小肋骨交叉
很简单：当有很多路口时，结果是“稀饭”；当它不够时，则图片看起来“更干净”

相邻的峰彼此接近，不相邻的峰则很远。
根据定义，图是一组顶点和一组顶点之间的连接。 使连接的顶点彼此靠近是表达图形数据基本属性的直接和逻辑方法。

社区聚集
这是从上一段得出的。 如果有很多节点之间的联系比图的其余部分更多，则它们形成一个“社区”，并且在图片中应该看起来像一个密集的簇

顶点和边的最小叠加
很明显。 如果我们在这里不能分辨出一个或多个对象，那么可视化效果将很差。

均匀分布顶点和/或边缘
如果图形的属性不允许另外确定至少某些结构，则此条件很有用。 例如，如果我们有整个图-它是一个密集的簇，那么最好在图片中涂抹它以至少查看连接的不均匀性，而不是使其融合为一个实心点。

样式是什么

我认为考虑这三种样式非常重要，尽管分类和类型很多。 但是，这些类型的知识足以导航主题。

• 力导向和基于能量
• 降维
• 节点功能

力导向和基于能量

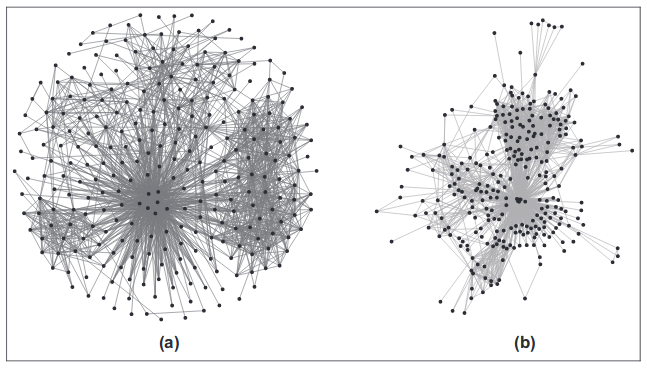
这些方法使用物理强度的模拟。 峰表示为彼此排斥的带电粒子，而边缘表示为将相邻峰拉在一起的弹性线。 然后，模拟这种系统中的顶点运动，直到建立稳定状态为止。 其他方法尝试描述这种系统的势能，并找到与最小值对应的顶点位置。

这一系列算法的优点如图所示。 通常，会获得一个非常好的样式，以反映图的拓扑。 在需要配置的参数中存在缺点。 好吧，当然还有计算复杂性。 对于每个顶点，您需要计算从所有其他顶点作用的力。

重要的族算法是Force Atlas，Fruchterman-Reingold，Kamada Kawaii和OpenOrd。 后一种算法使用了棘手的优化，例如，切掉长边以加快计算速度，并且副作用是，获得了更密集的近峰簇。

降维

该图可以由邻接矩阵定义，即由方矩阵NxN定义，其中N是顶点数。 这可以解释为N维空间中的N个对象。此表示形式允许使用通用的降维方法，例如tSNE，UMAP，PCA等。 另一种方法是基于边缘的权重和局部拓扑的知识来计算顶点之间的理论距离，然后在移入较小尺寸的空间时尝试保持这些距离之间的关系。

基于功能的布局

通常，数据来自真实世界，我们不仅拥有有关顶点邻接的信息。 峰是一些具有自己属性的真实对象。 记住这一点，我们可以使用顶点的属性在平面上显示它们。 为此，您可以使用任何常用的表格数据方法。 这些是减小上述PCA，UMAP，tSNE，自动编码器尺寸的方法。 或者，您可以为特征对绘制一个简单的散点图（散点图），并在结果视图的顶部绘制边缘。 另外，我们可以提到Hive Plot-一种有趣的方法，当属性的值对应于从中心指向的不同轴时，顶点位于该轴上，并且边缘之间用弧线绘制。

大图可视化工具

尽管可视化任务是古老且相对流行的，但是用于大型图形的工具仍然存在很大的问题。 不支持大多数。 几乎每个人都有一些严重的缺点，必须克服。 我只会谈论那些值得一提并且可以用于大型图形的图形。 对于小型图形，没有问题-这些工具易于找到并且基本可以正常使用。

GraphViz

直到2011年的比特币区块链交易和地址


配置设置可能很困难

具有自己的图形描述语言-点的老式CLI工具。 实际上，这是一个在任何情况下都具有不同样式的程序包。 对于大型图形，有一个sfdp工具-它属于“强制定向”堆叠类。 从命令行启动此工具的优缺点。 这对于重现性和自动化非常方便，但是，如果没有滑块和显示中间结果，设置参数将变得非常痛苦。 我们设置参数，开始，等待，没有进度条，查看结果，更改参数，重新启动。 能够以svg，png和其他图片格式编写。

杰斐

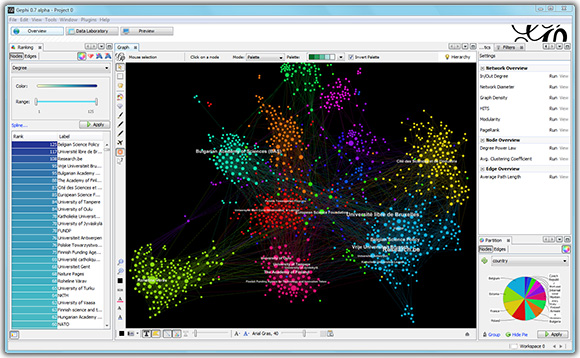
向iMDB推荐17.3万部电影


几百万个峰已经太难了

也许是整体上最强大的工具。 这是一个GUI应用程序，其中包含一组基本样式以及许多其他图形分析工具。 gephi社区已经编写了许多插件，例如我最喜欢的Multigravity Force-Atlas 2或用于将样式导出到交互式网页的插件。 同样，原始的OpenOrd实现包含在Gephi中。 Gephi具有用于根据顶点和边缘的属性绘制顶点，设置标题，尺寸和其他渲染选项的工具。 可以导出到主要图像格式，包括矢量。

一个非常令人讨厌的事实是，Gephi已经被废弃了几年。 两家主要的开发人员没有资源将其进一步开发所必需的知识转移给其他人，他们表示他们将无法再积极支持Gephi。 其他缺点包括界面有些“发臭”，缺少任何明显的功能，但是没有人“仅是更好”。 从最新消息来看，该项目的博客中有一条声明说，现代WebGL的功能已经领先于旧的Gephi，并且有机会看到它作为Web应用程序而复兴。

图

lastfm中的音乐推荐图。 来源在这里 。

人们不能不为这个用于图形分析的通用软件包致敬。 igraph的作者之一做出了他那个时代最壮观的图形可视化作品。 为此，他开发了DrL样式。 这是来自lastfm乐队的推荐图表。 结果更高。

缺点包括令人反感的文档。 至少要使用python api。 立即阅读源代码更加容易。

LargeViz

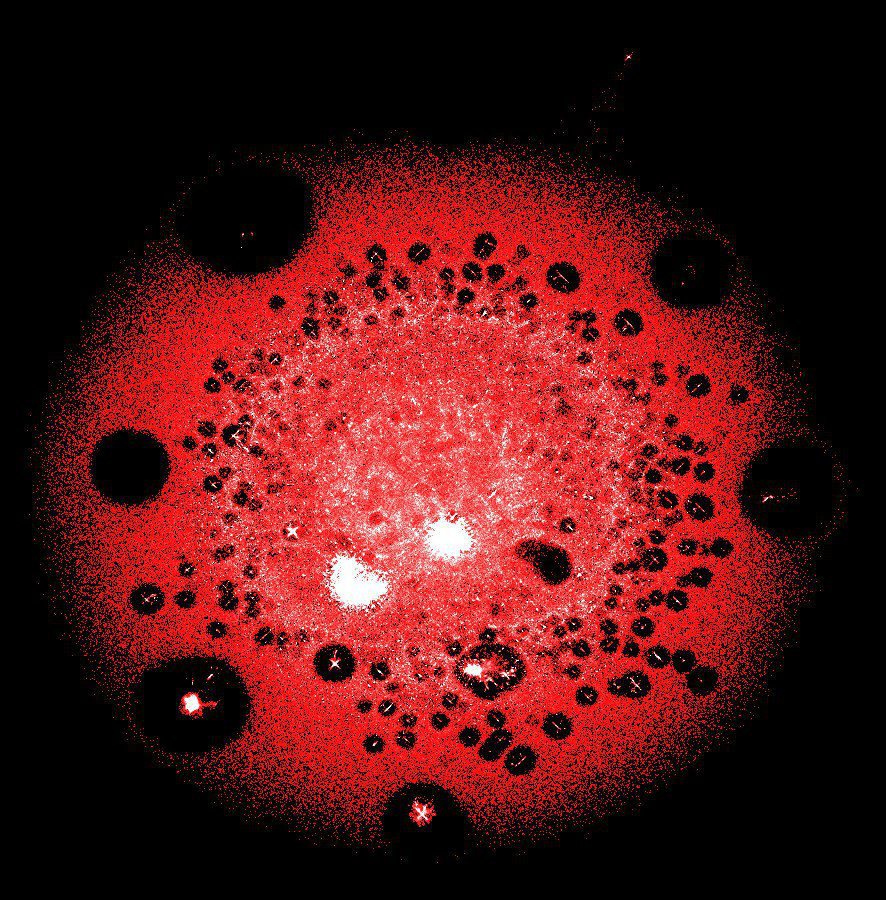
最大的比特币区块链集群之一中的几千万个峰（交易和地址）

当您需要绘制巨型图形时真正的救赎。 LargeViz是指降维算法，不仅可用于图形，还可用于任意表格数据。 它可以从命令行运行，并具有出色的性能。 内存非常经济且快速。

图形学

一周内可入侵的地址及其交易


清晰但非常有限的界面，合理的默认设置

此列表上唯一的商业工具。 Graphistry是一项服务，可获取您的数据并对其进行大量计算。 客户端只是在浏览器中查看精美图片。 实际上，gephi并不比合理的默认选项和交互性好。 它仅实现一种样式：类似于ForceAtlas。 顶点或边的最大数量限制为80万个。

图嵌入

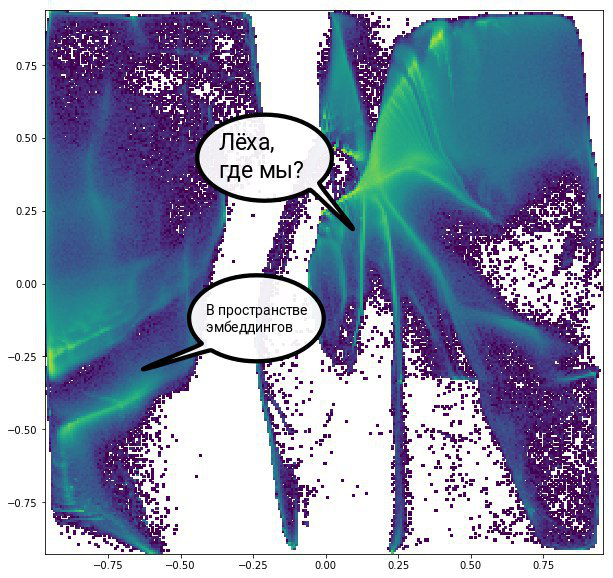
对于疯狂的尺寸，还有一种方法。 在绘制时，已经从一百万个顶点开始，仅查看空间中不同点的顶点密度是有意义的，这仅仅是因为看不到其他任何东西。 专门为渲染图形而发明的大多数算法，即使不是几天，也可以在数千万个顶点或边上工作数小时。 您可以通过解决一个稍微不同的问题来摆脱这种情况。 有许多方法可以获取给定维的向量表示，以反映图的顶点的属性。 接收到此类表示后，仅需将尺寸减小为2即可获得图片。

Node2Vec

Node2Vec + UMAP

将常规word2vec调整为图形。 代替单词序列，取顶点序列用于图形的随机遍历，并将其发送到word2vec而不是单词。 该方法仅考虑有关顶点邻域的信息。 通常这足够了。

诗句

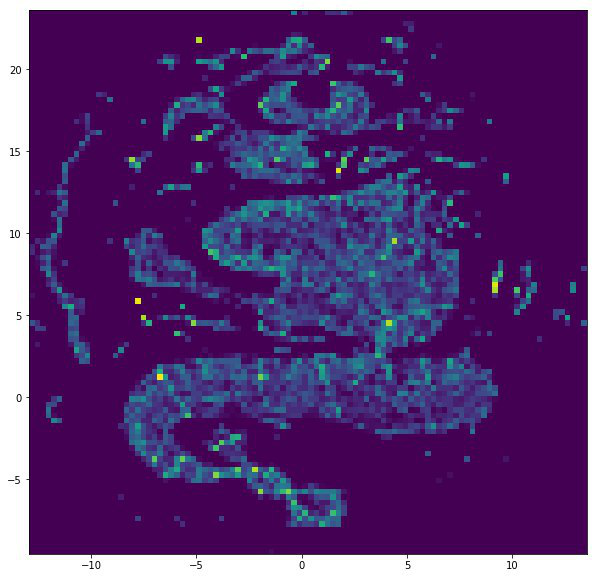
VERSE + UMAP

一种用于获取图嵌入的高级算法，该算法试图获得顶点的通用表示，即考虑到顶点在图中所扮演的所有角色。 考虑了顶点的邻域和图的局部拓扑。

图卷积

图卷积+自动编码器

有很多方法可以确定图上的卷积运算，但是从本质上讲，这是图上信息的“拖尾”，因此顶点可以接收有关其邻居符号的信息。 您可以将本地拓扑信息添加到这些属性。

奖励：关于图卷积的更多知识

所有描述的方法都基于一些现成的工具。 后一种情况是例外。 要实现图卷积，您需要考虑一下并编写一些代码。

关于图和其他非欧几里德数据的卷积的详细分析是值得单独撰写的主题。 在这里，我将描述最简单的基本方法，该方法不需要特殊的图形框架，并且易于扩展。 因此，我们希望图的每个顶点的符号都包含有关邻居符号的信息。

我们该怎么做？

最明显的方法是简单地取邻居的平均值。 如果您对发生的事情和平均值丢失的信息有更多的了解，则可以在其中添加其他统计信息，例如标准差，最小值，最大值等。

现在如何组织？ 首先，图实际上是许多顶点和许多边。 我们只对来自多个顶点的连接件感兴趣，因此在我们的案例中，边列表完全定义了图形。 这可以方便地以表格的形式编写：在第一列中，从中出现边的顶点在第二列中，这些边进入的顶点。 接下来，我们需要阅读统计信息。 这是一项非常常见的任务，因此您可以使用根据我们的情况进行了优化的框架。

表框架在图形分析中的作用

我们得出的结论是，我们有一个标明图表的标牌，并且需要读取一些数量的统计信息。 表格和统计信息-所有这些都以大熊猫为单位，因此以下将是其中的实现示例。

首先，让我们设置图表：

ara = np.arange(101).reshape(-1, 1) sample = np.vstack((np.hstack((ara[:-1], ara[1:])), # forward links np.hstack((ara[1:], ara[:-1])))) # backward links 

如图所示，这只是一个101个顶点相互连接的链。



然后我们随机设置顶点的符号：

 feats = np.random.normal(size=(101, 10)) 

我们将从这一切制作熊猫数据帧：

 edges = pd.DataFrame(sample, columns=['source', 'target']) cols = ['col{}'.format(i) for i in range(10)] feats = pd.DataFrame(feats, columns=cols) feats['target'] = ara 

现在我们设置卷积函数本身：

 def make_conv(edges, feats, cols, by, on, size=1000000, agg_f='mean', prefix='mean_'): """ edges -- edgelist: pandas dataframe with two columns (arguments by and on) feats -- features dataframe with key column (argument on) and features columns (argument cols) by -- column in edges to be used as source nodes on -- column in edges to be used as neighbor nodes size -- number of unique source nodes to be used in one chunk agg_f -- can be interpreted as pooling function. Pandas has several optimised functions for basic statistics, that can be passed as string arg (see pandas docs), but you also can provide any function you like prefix -- prefix for new column names """ res_feats = [] # used to stack result chunks # get chunk of unique source nodes for chunk in tqdm(chunker(edges[by].unique(), size=size), total=(len(edges[by].unique()) // size) + 1): # for each chunk we get feature matrix for neighbours temp = edges[edges[by].isin(chunk)]\ .merge(feats, on=on, how='left') # convolve and pool tempgb = temp[cols + [by, on]]\ .groupby(by).agg({col: agg_f for col in cols}).reset_index() res_feats.append(tempgb.rename(columns={c: prefix + c for c in cols})) # concat results return pd.concat(res_feats, axis=0).reset_index(drop=True) 

这是怎么回事

首先，我们选择一块顶点，对其进行卷积，将其所有边缘取整，将其与邻居的符号连接起来，然后将其写入临时数据帧。 然后，我们将源的顶点分组，并使用函数agg_f进行汇总，该函数默认情况下只是平均值。 将当前作品的结果添加到列表中，最后将结果串联起来。


对于此图，它看起来像这样


我们应用该函数并绘制结果：

 conv1 = make_conv(edges, feats, cols, 'source', 'target') plt.figure(figsize=(3, 8)) plt.imshow(np.hstack((feats[cols].values, conv1.values[:, 1:])), cmap='jet'); 

初始符号，然后是原始和第一次卷积的结果，然后是原始和两次卷积的结果。


例如，特别选择了这样一个简单的案例，如果您直接绘制符号矩阵，则很容易在视觉上看到符号在邻居中是如何“涂抹”的。 在更一般的情况下，该过程如下所示：

如果您想要更多数学

如果您以前听说过图卷积，那么很可能是在图卷积网络（Graph Convolutional Networks-GCN）的上下文中。 在某些情况下，此处介绍的数位板技巧似乎“并不难”。 实际上，有一篇非常有趣的文章专门讨论了无需深度学习的图卷积的使用：“简化图卷积网络”。 它给出了卷积的定义 $$$H ^ {（k）} \ leftarrow SH ^ {（k-1）}$在哪里 $$$H$是功能矩阵，并且 $$$S$是图的标准化拉普拉斯算子，其定义如下： $$$S = \波浪线{D} ^ {-\ frac {1} {2}} \波浪线{A} \波浪线{D} ^ {\ frac {1} {2}}$在这里 $$$\波浪号{A}$图的邻接矩阵是否与恒等矩阵相加，并且 $$$\波浪号{D}$-在对角线中记录图形顶点度数的矩阵。 所有这些都是使用scipy和numpy在python中用几行代码编写的：

 S = sparse.csgraph.laplacian(adj, normed=True) feats_conv = S @ feats 

sparse是scipy内部用于处理稀疏矩阵的模块，adj是邻接矩阵，feats和feats_conv是卷积前后的符号。 这种方法较为严格，但扩展性很差。 此外，如果您对所发生的事情的含义进行了一点思考，那么这等同于顶点处要素的值与顶点邻域中的平均值之间的差，也就是说，如果您添加一个操作，则可以由之前的表格方案完全解决。

参考文献

图形可视化评论
leonidzhukov.net/hse/2018/sna/papers/gibson2013
arxiv.org/pdf/1710.04328.pdf

简化图卷积网络
arxiv.org/pdf/1902.07153.pdf

GraphViz
graphviz.org

杰斐
gephi.org

图
igraph.org

LargeViz
arxiv.org/abs/1602.00370
github.com/lferry007/LargeVis

图形学
www.graphistry.com

Node2Vec
snap.stanford.edu/node2vec
github.com/xgfs/node2vec-c

诗句
tsitsul.in/publications/verse
github.com/xgfs/verse

带有完整熊猫包装代码的笔记本
github.com/iggisv9t/graph-stuff/blob/master/Universal%20Convolver%20Example.ipynb

图卷积
这是图卷积网络上的收集作品： github.com/thunlp/GNNPapers

整个文章的精髓归于一个表格