
许多比特币钱包在选择要发送的硬币时更喜欢使用较大的硬币,其余额大于所发送的金额。 在每次这样的交易之后,形成找零硬币。 一段时间后,整个钱包里满是0.001(约合10美元)的硬币,现在已经没有钱可花了。 当我再次需要进行交易时,我想到是否有可能组装交易,以便不进行任何更改。 钱包顽固地提议“削减”另一枚较大的硬币,因此我决定用手摘硬币以收集必要的金额。 但是,事实并非如此简单:总和要么小于期望值,要么超过期望值。 结果,我决定应该有一种算法,您可以用该算法从硬币中收集所需的数量或更多。 事实证明,这不仅可行,而且效果很好,使我撰写了这篇文章。 但是首先是第一件事。
背包问题
背包问题是众所周知的:在背包的容量有限的情况下,将尽可能多的贵重物品装进背包。 在这种情况下,我们遇到了0-1背包问题 ,因为每个物品(硬币)只能在背包中包装一次。 另外,每个“项目”的权重与其值一致,因此我们正在处理一个更特殊的情况, 即子集总和的问题 。 维基百科建议使用遗传算法,但我决定使用动态编程来寻找精确的解决方案,因为这在资源方面是可以实现的,而且看起来很简单。
为了减少为背包任务选择硬币的问题,您需要对输入数据进行少量转换。 事实是,解决背包问题(更确切地说是子集的总和)将为我们提供原始集合的一个子集,其最大数量不超过参数(背包携带能力)。 但是我们对硬币的组合不满意,因为硬币的数量少于我们要发送的数量。 但是,我们对稍微优越的组合感到满意。 例如,如果我们需要发送0.005比特币,并且发现一个组合可以提供0.00499,那么这对我们来说是无用的,因为它小于卖方想要的数量。 但是,如果我们找到0.005001,那是对的。 额外的satoshiki可以用作佣金(我们将在下面详细讨论),或者如果卖方允许发送更大的金额,则可以将其交给卖方。 因此,借助背包问题,我们不需要选择需要发送的硬币,而是选择需要留下的硬币。 那么就原始问题而言,最大程度的“短缺”将变成“破产”。
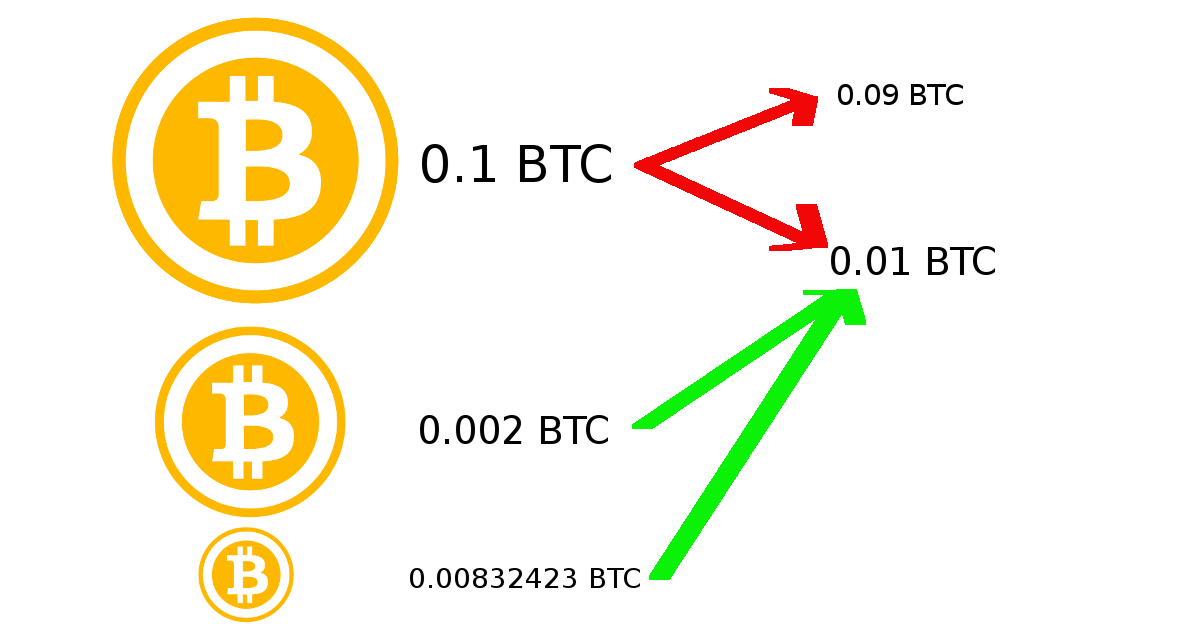
一个例子。 假设我们有这样的硬币:0.1 BTC,0.002 BTC,0.00832423 BTC。 我们需要发送0.01 BTC。 我们将找到这样的硬币,其总和将是最大的,但小于或等于我们的硬币的总数量减去发送的数量,即该数字:0.1 + 0.002 + 0.00832423-0.01 = 0.10032423。 在这种情况下,简单的搜索就会发现它是0.1个硬币。 我们将其保留,这意味着我们将发送其余的:0.002 BTC和0.00832423 BTC,它们总共给出0.01032423 BTC,这大于0.01 BTC并且适合我们。 (的确,佣金约为3美元,但我们说网络很忙,我们希望尽快进行发送。)
佣金
为了考虑交易费用,我修改了每个输入硬币,将其余额减少为将其包含在交易中作为输入必须支付的金额。 这可以通过知道输入的大小和佣金(例如,每个字节2个聪)来完成。 此外,我修改了要发送的金额,并在其中增加了不依赖于所选代币的交易部分的价格:标题和退出。 用户可以使用标志指定所有这些参数。 通常,您还可以通过指定每个字节0个Satoshi的佣金来禁用佣金的调整。
我从以下地址获取了有关不同版本地址(经典,包装的隔离见证和本机隔离见证)中输入和输出大小的信息: https ://bitcoin.stackexchange.com/a/84006
算法与实现
我立即放弃了遗传算法,也许是徒劳的。 专注于准确的算法。 我的第一个尝试是通过详尽搜索所有组合来实现,但即使使用40个硬币,它也要工作数小时,并且不得不放弃。 然后,我尝试了Wikipedia上建议的动态编程。 在其中,您不能将整个矩阵保留在内存中,而只能保留当前和前一行。 另外,我们不需要存储该值,因为它与权重一致并且是列号。 但是我们需要记住这种组合-我决定以位集的形式存储它。 此外,您只能存储一行,并从该行开始构建下一行。 每个非零行记录都保留在其位置,并被复制(加上相应的位)到另一个单元格中,该单元格位于右侧一定数量的单元格中(如果该位置之前为空)。 如果以相反的顺序进行排序,则对“跳转”所在的单元格进行排序,则可以正确填写所有内容:

当前行中的每个非零单元格本身都会在下一行中生成,并在右侧为特定数量的单元格(等于所添加硬币的值)生成另一个单元格。 如果该单元格中已经有一个值,那么在其他条件相同的情况下,由于我们希望发送尽可能少的硬币,因此选择(即不包括在交易中)硬币数量最多的选项“获胜”。
在一个单元格上,我花了8个字节用于位集,单元格的数量等于从0到硬币数量减去发送数量的可能余额数。 例如,如果钱包中只有1个比特币,并且发送了0.1个比特币,那么将有100'000'000-10'000'000 = 90'000'000个单元,每个单元为8个字节,即720兆字节-对于现代计算机来说是很少的。 如果硬币的数量少于32个,则每个硬币可以使用4个字节,但是我没有对其进行优化。 另外,如果有64个以上的硬币,则该程序将不起作用-这也必须通过制作任意长度的位集来解决。 最后,您可以舍弃天平中的最后一个符号,从而失去一些准确性,但可以赢得10次内存。 但是到目前为止,它会做到的。
我将程序不变地调用,并将其放在gitlab上: gitlab.com/starius/changeless 。 它是用Go编写的,照常使用go get组装。 CI中提供了适用于Linux,Windows,Mac的二进制文件 。
当我用真实的硬币启动该程序时,我为她选择所需组合的准确性感到惊讶。 当硬币数量很大时,几乎可以选择与硬币余额相称的任何数量,精确度可低至satoshi! 您更改了1个satoshi的所需金额,程序就为该金额提供了完全不同的硬币组合。 以下是使用50个随机硬币(余额为0到1个比特币)的示例。
$ cat coins50.txt 0.01331611 0.03906237 0.04847086 0.08453118 0.09748168 0.10395389 0.10619825 0.12156721 0.12923149 0.13587973 0.14798976 0.16053788 0.19011834 0.21570038 0.21946913 0.31861430 0.33435508 0.33718842 0.33789473 0.35976748 0.37360122 0.44944553 0.47572926 0.49927495 0.50992142 0.53062326 0.53079433 0.53542072 0.54715225 0.55019714 0.55313907 0.56656642 0.56673333 0.65879650 0.66228482 0.68424322 0.70436496 0.75638055 0.79095597 0.82438005 0.83684407 0.85151564 0.86862948 0.90054250 0.90239402 0.91636213 0.93087757 0.93579251 0.97207439 0.98248384 $ changeless -amount 10.00000000 -coins coins50.txt Processing item 50/50. 0.09748168 + 0.33435508 + 0.47572926 + 0.53542072 + 0.66228482 + 0.70436496 + 0.75638055 + 0.82438005 + 0.9005425 + 0.90239402 + 0.91636213 + 0.93579251 + 0.97207439 + 0.98248384 = 10.00004651 Tx size: 2118 vBytes. Total fees: 0.00004651 BTC (2.2 sats/vByte). $ changeless -amount 10.00000001 -coins coins50.txt Processing item 50/50. 0.01331611 + 0.09748168 + 0.53079433 + 0.56656642 + 0.70436496 + 0.75638055 + 0.82438005 + 0.86862948 + 0.9005425 + 0.91636213 + 0.93087757 + 0.93579251 + 0.97207439 + 0.98248384 = 10.00004652 Tx size: 2118 vBytes. Total fees: 0.00004651 BTC (2.2 sats/vByte).
该程序设法提取硬币组合,以发送正好10个比特币和正好10.00000001个比特币(10个比特币和1个satoshi)。 要看到这一点,您必须从硬币金额中减去佣金:10.00004651-0.00004651 = 10,10.00004652-0.00004651 = 10.00000001。
如何获得硬币余额清单
对于Electrum程序,我发现是这样的(控制台命令):
' '.join((x["value"]) for x in listunspent())
如果您想排除某些硬币,例如在某个地址,则可以这样进行:
' '.join((x["value"]) for x in listunspent() if x["address"] != "bad address")
对于其他钱包,我没有找到这么简单的方法,只能用手重新输入。