正算术：克服自己领域中的浮点数。 第一部分

第二部分

来自翻译者：Posit格式的主题已经在此处成为中心，但是没有重要的技术细节。 在本出版物中，我提请您注意John Gustafson（Posit的作者）和Isaac Yonemoto关于Posit格式的文章的译文。
由于文章量很大，因此将其分为两部分。 链接列表在第二部分的末尾。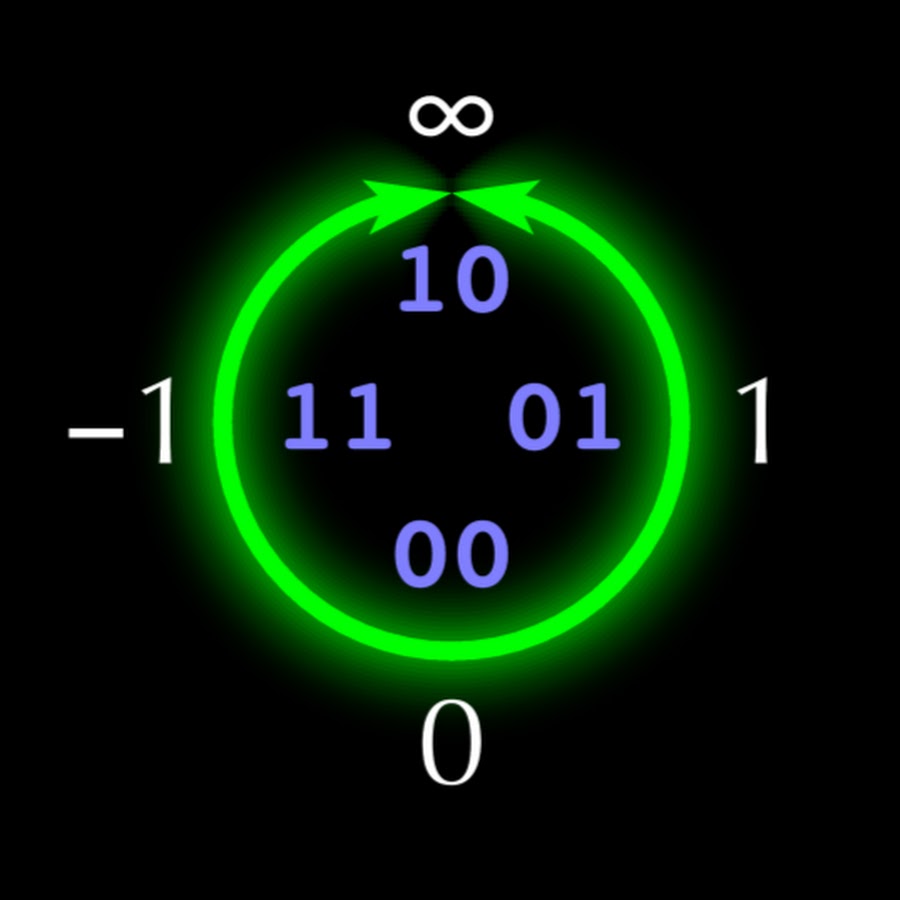



这种称为posit的新数据类型被设计为直接替代IEEE标准754的浮点数。与早期形式的unum算术不同，posit标准不需要使用间隔算术或可变大小的操作数，并且浮点数，如果无法精确表示结果，则将四舍五入为正。 与浮点格式相比，它们具有不可否认的优势，包括更大的动态范围，更高的精度，在不同系统上的计算结果按位重合，更简单的硬件以及对异常的更简单支持。 posit数不会溢出到无穷大或为零，并且“非数字”（Not aNumber，NaN）是动作，不是位组合。 posit处理单元没有IEEE FPU复杂。 它消耗更少的功率，并占用较小的硅片面积，因此与FLOPS相比，在相同的硬件资源下，该芯片可以每秒执行更多的正数运算。 尤其是GPU和深度学习处理器，每瓦功耗可以执行更多操作，这将提高其工作质量。

进行了综合测试，比较了各种位置精度下的位置精度和浮动精度。 在可以接受低精度的情况下，低精度的正数是“粗略计算”的最佳解决方案。 高精度的位置编号比相同大小的浮点数提供更高的精度；在某些情况下，32位位置数可以安全地替换64位浮点数。 换句话说，posit在其自己的游戏中胜过浮动。

理论：Unums：I型和II型

算术框架unum （通用数字，通用数字）具有几种表示数字的形式。 原始形式是“类型I”，它是IEEE 754的超集； 她在小数部分的末尾使用ubit来表示实数是准确的或在相邻实数之间的范围内。 尽管Unum像float一样具有符号，指数和小数部分，但指数和小数部分的长度会自动变化，从一位到用户定义的某个值。 I类型的Unum是表示区间算术的紧凑方法，但是可变长度需要额外的精力。 此类型可以通过使用特殊的舍入函数来重复浮动的行为。

“类型II”通用数字格式[4]与IEEE浮点数不兼容，它是一个基于投影实数 x的简洁，数学上严格的概念。 这里的关键思想是附加代码中的带符号整数可以优雅地映射到投影实数，具有从正数切换为负数的相同属性，并且在数字轴上具有相同的顺序。 引用威廉·卡汉[5]：
他们之所以节省内存空间，是因为它们不操纵数字，而是操纵值的指针。 这样就可以非常快速地进行算术运算。”
5位unum的结构如图2所示。 1.如果每个unum有n位，则“ u-晶格”将圆的右上象限填充一组有序 $$$2 ^ {n-3} -1$ 实数 $$$x_i$ （不一定是理性的）。 在左上象限为负 $$$x_i$ 相对于垂直轴反射。 圆的下半部分包含与上半部分的数字相反的数字（从水平轴反射），这使得乘法和除法运算与加减法一样对称。 与类型I一样，类型II的unum数以1 （ubit）结尾，表示unum以0结束的相邻精确点之间的开放间隔。


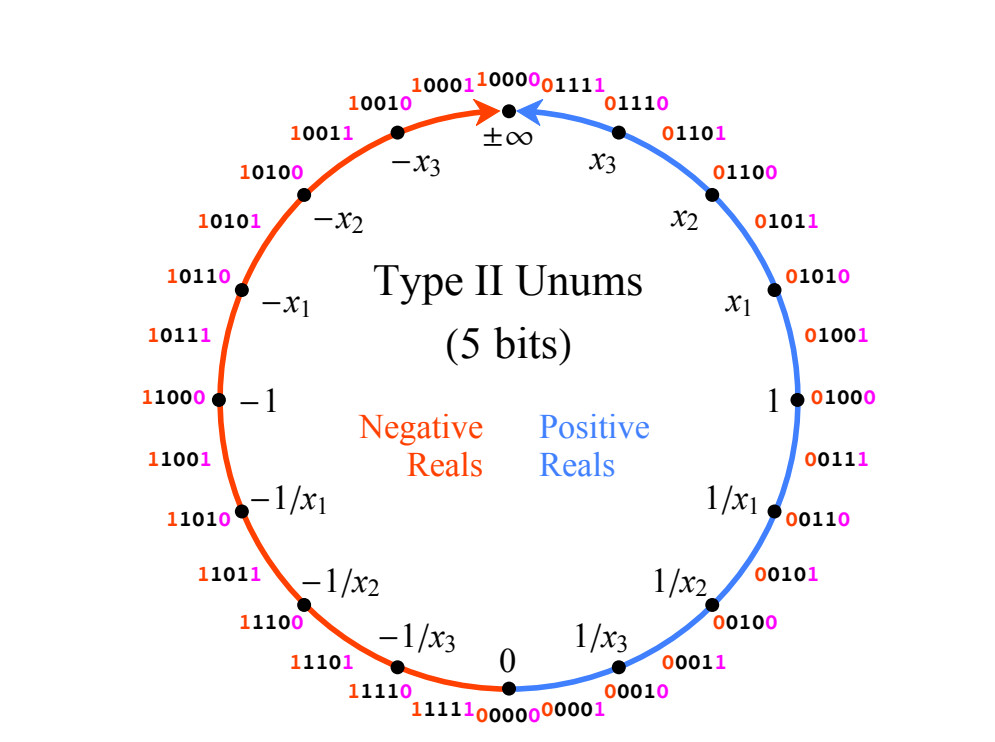图 1.投影实数线，以4位长的附加代码映射到整数。

II型unum数具有许多理想的数学属性，但是使用它们的大多数操作都是使用查找表完成的 。 如果需要n个精度位，则该表（在最坏的情况下）将具有 $$$2 ^ {2n}$ 两个参数函数的值，但考虑到对称性和其他技巧，可以将表缩小为更可接受的大小。 表格的大小将这种超快格式的规模限制为当今技术的20位或更少。 II型普通数字也不适合合并操作。 这些缺点促使人们寻找一种格式，该格式保留了II型数字的许多特性，但更“硬件友好”，可以通过类似于现有FPU的逻辑电路进行计算。

2.正确数字

实数计算有两种相反的方法：

• 不严格，但是便宜，并且可以被大量实际应用接受
• 数学上严格，即使以时间和内存为代价

第一条与舍入误差足够小的实数算法有关，第二条与区间算术有关。 I和II型的单数也可以类似地考虑，这就是为什么它们是“通用数”的原因之一。 但是，如果每次操作后总是要使用一些函数进行舍入，则最好不要将最后一位用作小数部分的有效位，而不要用作ubit。 这种类型的数字unum将被称为数字posit。

摘自《新牛津美国词典》第三版：

posit （名词）： 以事实证明为事实的陈述。

为了简化硬件实现，类型II的unum削弱了以下规则之一：确切的反值仅存在于0， $$$\ pm \ infty$ 和度二。 这使我们可以填充u-grid，以便最终数字保持与float相似，并具有以下形式 $$$m \ cdot2 ^ k$ 其中k和m是整数。 没有开放时间间隔。

有效的是一对大小相等的正数，每个正数以ubit结尾。 它们旨在用于那些必须严格确定数字间隔（例如在调试数值算法时）的应用程序。 有效值比普通的区间算术功能更强大，并且不太容易迅速扩大过于悲观的区间边界[2，4]。 但是，它们不是本出版物的主题。

图2显示了具有指数位的n位位置表示的结构。


图2.尾随非零值的通用位置格式

符号位包含0表示正数，1表示负数。 对于负数，请在对模式，指数和小数部分解码之前找到补充2。 要了解模式位，请考虑表1中所示的二进制字符串，其中k表示前导序列的长度，而比特流中的x表示无关状态。

表1.游程长度，表示状态位的k



我们将前导序列的长度称为数字模式。 二进制字符串以一定数量的零或一开始，然后是相反的位，或者到达字符串的末尾。 模式位以琥珀色突出显示，相反的位以棕色突出显示。 令m为序列中相同位的数目，如果这些位为零，则k = -m，如果为1，则k = m-1。 大多数处理器可以在硬件中找到一个单词中的第一个单元，或者找到一个单词中的第一个零，也就是说，解码逻辑已经可用。 模式表示比例因子等于 $$$已使用^ k$ 在哪里 $$$useed = 2 ^ {2 ^ {es}}$ 。 表2显示了使用值的示例。

表2.用作es函数



接下来的位（在图中以蓝色突出显示）是指数e，它表示无符号整数。 它不会像浮动中那样移动，它表示缩放到 $$$2 ^ e$ 。 可能最多有es个指数位，具体取决于模式位右边剩余多少位。 这是一种更改精度的紧凑方法；绝对值接近1的数字比非常大或非常小的数字（在计算中不那么常见）具有更高的精度。

如果在模式和指数位之后还有剩余位，则它们代表小数部分f，就像浮点数格式的小数部分1.f一样，但隐藏位始终为1。与浮点数不同，没有隐藏0的非规格化数字。

我们描述的系统是填充u-grid的自然结果。 为了清楚起见，让我们从一个简单的3位位置开始。 图3仅显示了投影实数的右半部分。 因此，图中的数字。 3.遵守II类规则。 只有两个特殊值：0（所有位均为0）和±∞（一个单位，后跟全零），它们的位序列不遵循位置符号。 对于图3中的其他正值，这些位如上所述进行了着色。 请注意，图3中的所有正值都是以度数k表示的以度k表示的精确使用值。


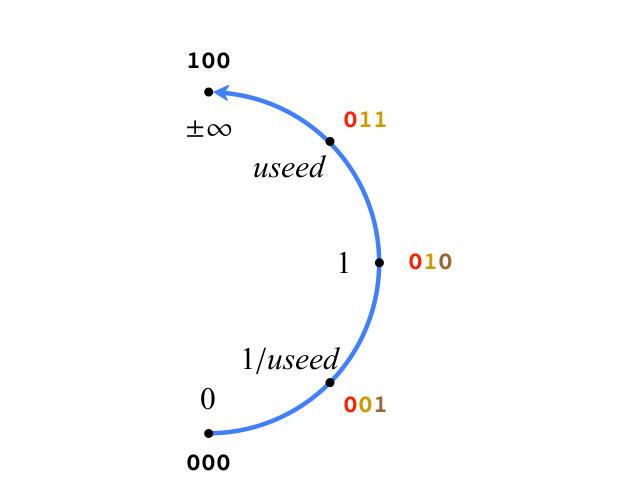图3。 3位正数的正值

位置数的精确度随位的增加而增加，并且当位0时，值保持在圆上的位置；当位1加时，在圆上的两个正值之间创建一个新值。 我们应该给它们分配什么数值？ 令maxpos为最大正值，minpos为由位串定义的圆上的最小正值。 在图3中，使用了maxpos，使用了minpos 1。 插值规则如下：

在maxpos和±∞之间，新值是maxpos×使用； 在0和minpos之间，新值是minpos /已使用（带有新的模式位）
现有价值之间 $$$x = 2 ^ m$ 和 $$$y = 2 ^ n$ ，其中m和n相差大于1，则新值将是它们的几何平均值， $$$\ sqrt {x \ cdot y} = 2 ^ {（m + n）/ 2}$ （带有新的指数位）。
在其他情况下，新值位于现有x和y之间的中间，即算术平均值， $$$（x + y）/ 2$ （带有新的小数位）

例如，图。 图4显示了es = 2并因此使用= 16的2到5位正数的构造。


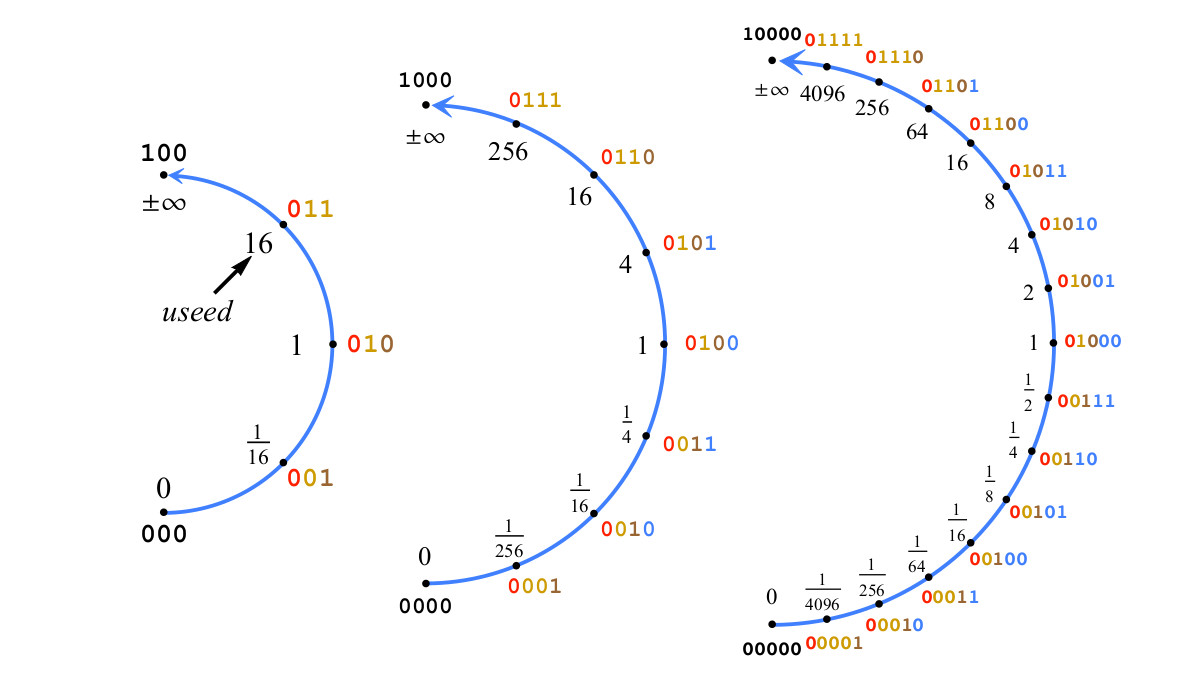图 4.用两位指数建立一个Posit， $$$es = 2，使用= 2 ^ {2 ^ {es}} = $ 1$

如果在图。 4再增加一位以获得6位正值，到表示1/16到16之间值范围的正数，将加小数部分的位，而不是指数位。 将表示数字posit p的一串字符串视为有符号整数，范围为 $$$-2 ^ {n-1}$ 之前 $$$2 ^ {n-1} -1$ 。 令k为代表模式位的整数，e为代表指数位（如果存在）的无符号数。 如果位是小数部分 $$$\ {f_1f_2 ... f_ {f_s} \}$ 可能为空，则让f为代表数字的值 $$$1，f_1f_2 ... f_ {f_s}$ 。 然后p代表

$$

$$x = \开始{cases} 0，＆p = 0，\\ \ pm \ infty，＆p = -2 ^ {n-1}，\\符号（p）\使用次数^ k \次数2 ^ e \次f \，＆\文字{any other} p \ end {cases}$$

模式位和es位与标准浮点型中的指数位执行相同的功能，它们共同确定比例因子等于2的幂，并且每个使用的增量均表示移位 $$$2 ^ {es}$ 一点。 maxpos的数量是 $$$已使用^ {n-2}$ 和minpos相等 $$$已使用的^ {2-n}$ 。 图5中显示了对正数进行解码的示例（为简单起见，使用es为“非标准”值）。


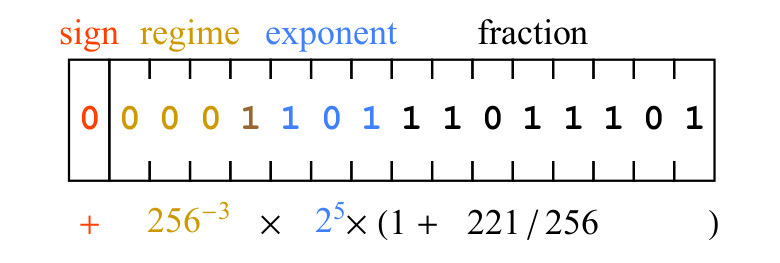图 5.正位字符串及其数学含义的示例

符号0表示该值为正。 模式0001的位具有三个零的序列，这意味着k = -3，因此，由模式的位引入的缩放因子为 $$$256 ^ {-3}$ 。 指数位101将5表示为无符号二进制整数，并且插入比例因子为 $$$2 ^ 5$ 。 最后，小数部分11011101的位代表数字221，即小数部分为1 + 221/256。 该表达式写在图5的位域下。 引导我们走向结果 $$$477/134217728 \约3.55393 \ times10 ^ {-6}$

2.2。 8位正则和神经网络训练

尽管IEEE标准未定义8位浮点数，但已证明es = 0的8位正数对某些目的很有用，但它们对于构建神经网络非常有用[3，8]。 当前，半精度（16位）IEEE编号通常用于这些目的，但是8位位置编号的处理速度可能会提高2-4倍。 神经网络中的一个重要功能是S形，它的渐近线为0，对于 $$$x \ to- \ infty$ 和1 $$$x \到\ infty$ 。 乙状结肠功能概观 $$$1 /（1 + e ^ {-x}）$ ，并且计算成本很高，并且由于除法的原因，很容易需要一百多个处理器周期才能从库中调用exp（x）函数。 使用正数，您可以简单地反转代表x的数字posit的第一位，将数字2右移，用零填充左边的位，并得到posit函数，如图6所示。 紫色，接近S形（以绿色显示），甚至在与y轴交叉时具有相同的斜率。


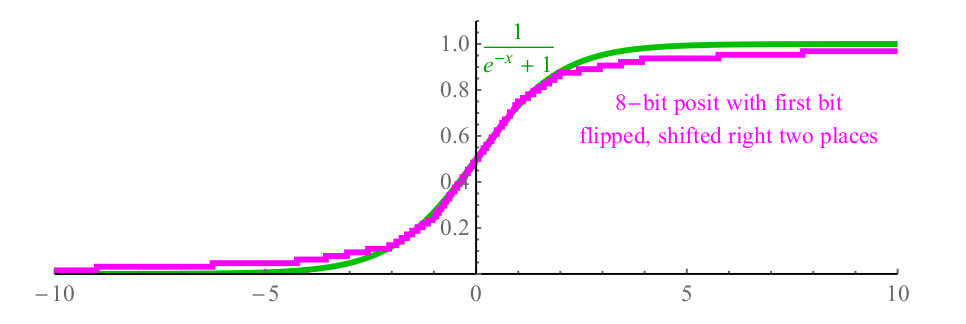图 6.使用位置表示法的快速乙状结肠功能

2.3。 用于达到和超过浮动的动态范围

我们将数字系统的动态范围定义为从最小最终最大值到最大正最终值（从最小位置到最大位置）的十进制顺序数。 也就是说，动态范围定义为 $$$log_ {10}（maxpos）−log_ {10}（minpos）= log_ {10}（maxpos / minpos）$ 。 对于es = 0的8位正数，minpos为1/64，maxpos为64，因此动态范围为3.6个十进制数。 用es = 0定义的正数是简洁，优雅的，但是与相同大小的IEEE浮点数相比，它们的16位和32位版本具有较小的动态范围。 例如，一个32位的IEEE浮点型的动态范围为83个十进制，但是es = 0的一个32位posit的动态范围仅为18个十进制。

下表是es值的表格，这些值允许正数超出16位和32位大小的float的动态范围，并接近64位，128位和256位大小的正整数。

表3.相等位数的float和posit的动态范围



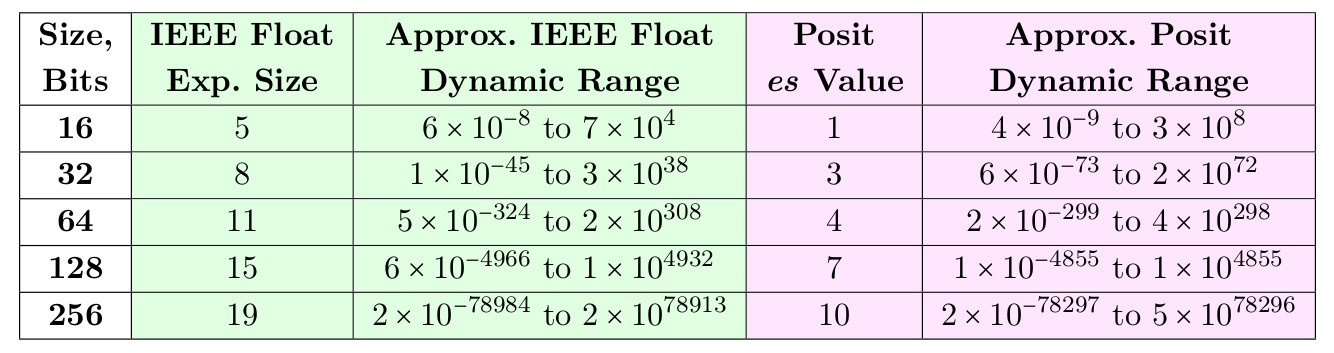
为32位位置选择es = 3的原因之一是，在这种情况下，它们不仅可以用作32位浮点数的简单替换，而且还可以用作64位。 同样，在当前使用32位浮点数的应用程序中，16位正整数的17年动态范围为它们铺平了道路。 我们证明，在相同的位大小下，posit在动态范围和精度方面都可以胜过float。

2.4。 浮点数和正数格式的定性比较

posit格式中没有“ NaN”，取而代之的是，计算被中断，并且中断处理程序必须报告错误或以某种方式处理该错误并继续计算，但是posit号不允许分配表示逻辑错误的特定值，顾名思义就是数字。 这大大简化了硬件。 如果程序员认为需要使用NaN值，则表明程序尚未完成，应在调试环境中使用有效的数字来查找和消除此类错误。 另外，posit没有 $$$+ \臭名昭著的$ 和 $$$-\臭名昭著的$ ，例如float，有效数字支持打开间隔 $$$（maxpos，+ \ infty）$ 和 $$$（-\ infty，-maxpos）$ ，这使得可以表示任何符号的无穷大值，而对有符号无穷大的需求将仅意味着您需要应用有效值，而不是正数。

同样在正视图中，不存在“负零”，负零，这是IEEE浮点标准中存在的另一个逻辑缺陷。 对于正数，如果a = b，则f（a）= f（b）。 IEEE 754标准说，与-0倒数的数字是 $$$-\臭名昭著的$ ，并且与+0相反的数字是 $$$+ \臭名昭著的$ ，但也表示-0为+0。 因此，可以理解 $$$-\ infty = + \ infty$ ？

浮点数具有复杂的a = b比较算法。 如果（a，b）中的任何一个为NaN，则比较结果始终为负，即使它们的位表示相同。 如果位表示形式不同，则由于负零等于正零，因此a仍然有可能等于b！ 在posix中，相等性检查与整数检查相同：如果位数相等，则数字相等。 如果有任何不同，则它们不相等。 正数与带正负号的整数具有相同的关系（a <b），与带正负号的整数具有相同的关系，您必须确保不会因正负号的更改而产生溢出，但是如果需要比较正负号，则不需要单独的机器指令比较带符号整数的说明。

在posit格式中，没有未归一化的数字，即没有特殊的比特组合显示隐藏的比特是0而不是1 。 Posit不使用反溢出，而是逐渐降低精度，从而提供了反溢出及其对称情况，溢出的功能（与posit不同，标准浮点数是非对称的，并使用这些位模式来表示大量无用的NaN值）。

浮点格式相对于假设条件有一个优势，当开发硬件时，指数位和小数部分的固定排列允许它们并行解码。在posit格式中，您需要遵循一些顺序，首先解码模式位，然后解码其余位。有一种解决此限制的简单方法，类似于用于提高float中异常处理速度的技巧：每个值附加一些额外的位，以便在解码指令时在其中存储大小信息。

3.按位兼容性和组合操作

IEEE浮点数在不同系统上不能给出相同结果的原因之一是因为对于基本功能，例如 $$$log(x)$ 和 $$根据IEEE标准的 c o s （x ）对于任何可能的输入都不需要精确到最后一位。 posit环境应正确舍入所支持算术运算的所有结果。 （一些数学库程序员担心“表困境”，即对于某些值来说，确定其正确的舍入可能会非常昂贵，可以通过使用插值表而不是多项式逼近来消除这种情况。）函数最后一位的值不正确$cos(x)$$$例如， e x最终可能导致计算机系统告诉我们2 + 2 = 5。IEEE浮点数在不同系统上不会产生重复结果的更根本原因是该标准允许使用隐蔽的方法来避免上溢/反溢出，并提高操作的准确性，例如在内部存储用于指数和小数的附加进位零件。正算禁止这种隐藏的技巧。$e^x$



IEEE 754标准的最新版本（2008）[7]在要求中包括组合的乘法加法运算。这是一个有争议的更改，未得到许多委员会成员的认可。在完成所有运算（包括精确的整数运算）之后，组合运算将舍入运算延迟到计算中的最后一个运算（包括多个运算）完成为止。组合运算与可扩展精度算法不同，后者可以增加整数的长度，直到计算机内存已满。

posit环境要求存在以下组合操作：

组合乘法加法$$（a × b ）+ c组合加法乘法$(a\times b)+c$
$$（a + b ）× c组合乘-乘-减$(a+b)\times c$
$$（a × b ）- （c × d ）组合求和$(a\times b)-(c\times d)$
$$∑ a i组合标量乘法$\sum a_i$
$$Σ 一个我b 我请注意，从上述列表中的所有操作是组合标量乘的一个子集[6]中的处理器的硬件需求方面。使用标量乘法可以获得的最小非零数是$\sum a_i b_i$

$$$minpos^2$ 。 任何乘积都是整数倍 $$$minpos^2$ 。 如果我们想得到向量的标量积 $$$\{maxpos, minpos\}$ 和 $${ m a x p o s ，m i n p o s }作为在暂存区域中的确切操作，我们需要一个足够大的整数来存储$\{maxpos, minpos\}$$$$maxpos^2/minpos^2$ 。 回想一下 $$$maxpos=useed^{n-2}$ 和 $$$minpos=1/maxpos$ 。 这样 $$$maxpos^2/minpos^2=useed^{4n-8}$ 。考虑到传输位和四舍五入的两位，我们获得表4中给出的推荐值。

表4.每种位置大小的精确电池大小



在某些情况下，电池大小可与寄存器大小相媲美；在其他情况下，则需要与L1或L2高速缓存等效的暂存区。组合的操作可以通过软件或硬件来执行，但必须可在实际环境中执行。