我们最近进行了一项实验，以测试一种降低LIGO中量子噪声的新方法，并撰写了一篇有关该文章的文章，请参见arXiv：
“通过EPR纠缠来演示干涉仪增强” 。 在这里，我将告诉您LIGO中什么样的量子噪声，如何减少它们，以及量子纠缠和压缩光与它有什么关系。
UPD文章发表在《
自然光子学》上 。
1. LIGO灵敏度和量子噪声
在
关于爱因斯坦望远镜的
上一期出版物中，我详细讨论了探测器的工作原理和里面有什么噪音。 该探测器具有多种噪声：地震，热，量子和其他噪声，并且它们都干扰重力波信号的配准。
对LIGO在不同频率下的灵敏度的主要贡献，已标准化为GW（应变）的幅度。创建重力波检测器的全部困难在于降低这些噪声。 这些噪声中的大多数不是基本噪声，而是技术限制。 而且，仅量子噪声是由测量设备的本质引起的。 它们将成为未来检测器获得更高灵敏度的主要障碍，因此我们将对其进行详细介绍。 有两种量子噪声：散粒噪声和辐射压力噪声。
散粒噪声是由于激光的量子性质而产生的：激光束由彼此之间具有不同随机延迟的光子组成。 当在光电二极管上测量这些光子时，光子通量的波动会导致电流波动，结果会导致我们观察到的信号产生噪声。
辐射压力的噪声是光的量子性质的第二面。 从
列别捷夫（Lebedev）的实验时代起，经典电磁学
就已经知道
，发光的物体会受到光的压力 。 如果我们将光子视为粒子，则很容易理解：每个粒子都带有一个脉冲，该脉冲在撞击时会传输到人体。 即，当激光照射在可移动镜上时，镜在光压力的影响下开始移动。 而且由于光子是随机分布的，因此在给定的时间间隔内，有时会有更多的光子到达反射镜，有时会更少，并且此光压力也是随机的。 因此：光的量化会导致随机力作用在LIGO中的镜子上。 该力引起反射镜的随机移动，该随机移动记录为干涉信号在干涉仪的输出处。
关于量子噪声的解释。 光子数量的随机分布会产生随机的辐射压力（左）。 另一方面，光子随时间的随机分布会导致光电探测器的振幅波动（右）。 两种噪声都取决于波长，光功率和肩长。 辐射压力的噪声越小，镜子的质量越大。 信用：[1]。入射到反射镜上的光的功率（即光子的通量）越大，辐射压力的噪声越强。 来自GW的信号也随着检测器中光功率的增加而增加。 归一化为信号的散粒噪声降低。 结果，您可以通过增加光的功率来增加受散粒噪声限制的灵敏度，但是您将不得不为辐射压力噪声的增加付出代价。 反之亦然。 经典方法无法同时抑制两个量子噪声。 将不得不使用量子技术。
灵敏度对光功率的依赖性：散粒噪声（蓝色）降低，辐射压力噪声（绿色）成比例增加。2.压缩光
关于哈布雷的
一篇精彩的文章是关于
qbertych的挤压光的。 如果您不知道什么是压缩光，强烈建议您先阅读他的文章。 我会简短。
如果将光视为波，则特征参数将不是光子通量及其之间的延迟，而是波的幅度和相位。 通常他们谈论光的相位和幅度
正交 。
$$显示$$ E = E_0 \ cos（\ omega_0 t + \ phi）= E_0 \ cos \ omega_0 t \ cos \ phi-E_0 \ sin \ omega_0 t \ sin \ phi = \\ = E_ {} \ sin \ omega_0 t + E_ {a} \ cos \ omega_0 t $$显示$$
如果我们感兴趣的信号包含在光的相位中，并且足够小，那么我们可以得出一个近似值：
$$显示$$ $$ E_ {f} = E_0 \ sin \ phi \大约E_0 \ phi; \ quad E_ {a} = E_0 \ cos \ phi \大约E_0 $$显示$$
因此，价值
$内联$ E_ {f} $内联$ 称为相位正交-它包含有关相位的信息。
因此，散粒噪声是光的相位的波动，并且辐射压力的噪声是由振幅波动引起的。
相位不确定性和振幅不确定性与海森堡关系有关：
$$显示$$ \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ {a} \ leq \ frac {1} {2} $$显示$$
在常规的激光束中，这些不确定性是相等的。 但是，可以通过增加幅度不确定度来
压缩相位中的不确定度-主要是它们的乘积满足不确定度关系。 这种光被称为挤压：
$$ display $$ \ Delta ^ 2 E_ {f} ^ {sqz} = e ^ {-2r} \ Delta ^ 2 E_ {f}，\ Delta ^ 2 E_ {a} ^ {sqz} = e ^ {2r } \ Delta ^ 2 E_ {a} \\ \ Delta ^ 2 E_ {f} ^ {sqz} \ Delta ^ 2 E_ {a} ^ {sqz} = \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ { a} \ leq \ frac {1} {2}，$$显示$$
其中r是压缩率。
一般而言，即使没有强光束，也始终存在
真空波动 。 它们也可以被压缩以获得压缩的真空：平均来说，其中的光子数为零，但是振幅和相位的波动被压缩了。
通过信号端口进入检测器的真空波动是LIGO中量子噪声的来源。 因此，如果此真空被同相压缩，则将减少检测器中的散粒噪声。
在过去的8年中，该方法已在GEO600检测器中使用，将散粒噪声降低了四倍，并且自今年以来，它也已在LIGO中实施，将散粒噪声降低了一半（这使记录的事件数增加了8倍）。
左：挤压光改善LIGO灵敏度的示例。 正确：几年前，我们小组创造了迄今为止最好的压缩效果：真空波动被抑制了15 dB。但是，一切并不是那么简单：根据不确定性关系，如果我们压缩相位，则会增加幅度波动。 并且它们增加了辐射压力的噪声。 同样，您必须选择通过增加另一种来降低噪声。 但是有可能以某种方式解决这个限制吗？
3.频率相关的压缩
幸运的是，两种量子噪声限制了检测器在不同频率下的灵敏度：在低噪声下，辐射压力比散粒压力强得多，而在高噪声下，辐射压力强于散粒压力。 因此，可以准备光的棘手压缩，其中在低频处，光的振幅被压缩（因此，辐射压力噪声被减小），而在高频时，其相位被压缩（因此，散粒噪声被减少）。
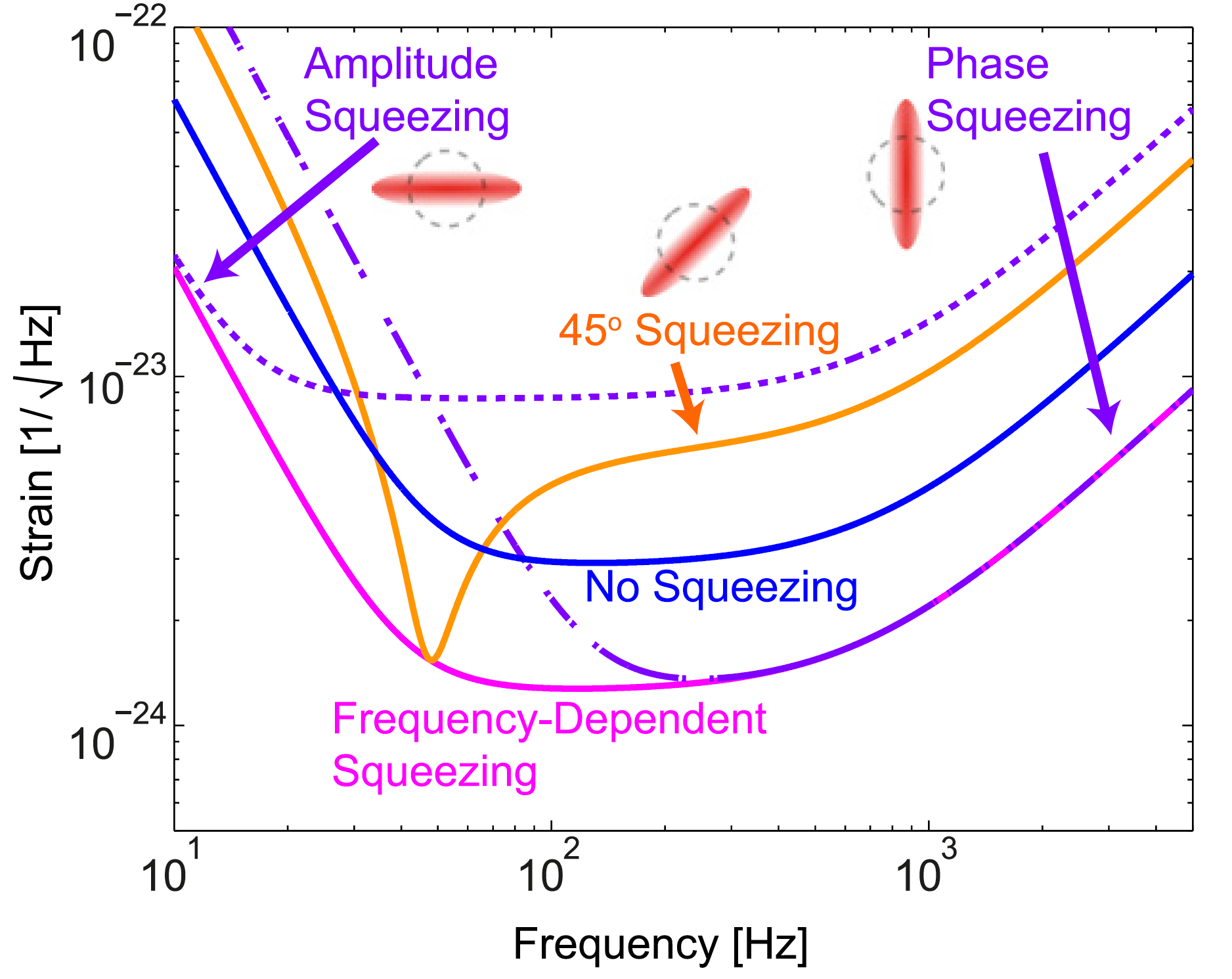频率相关的压缩：在不同的频率下，幅度，相位或其组合被压缩。 结果，在所有频率下灵敏度都得到提高。 [SSY Chua等，2014年。 量子引力 31 183001]从根本上讲，需要进行频率依赖性压缩的原因是，反射镜上的辐射压力也会产生光压缩，但正交度不同。 可以在下图中看到：如果在输入端使用常规压缩，由于辐射压力，它会在输出端获得频率依赖性。 要“取消”此频率相关性，您需要在输入端设置压缩的逆相关性。
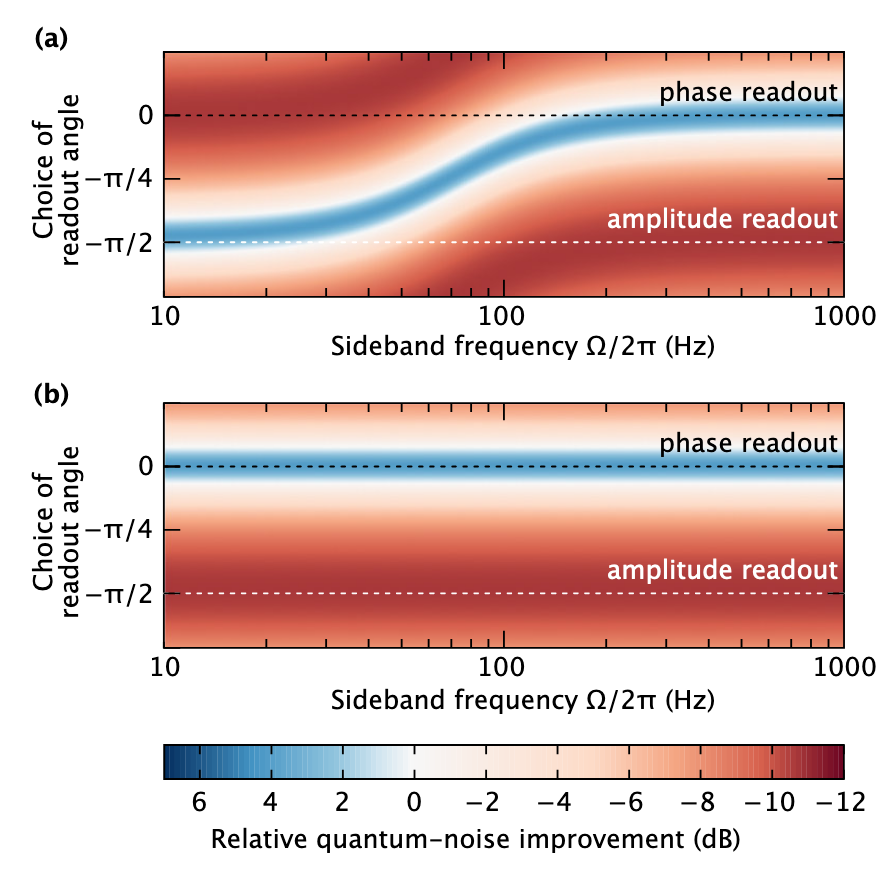文章中的一个例子：上面显示了使用常规压缩时干涉仪灵敏度随频率和不同测量相位而变化的依赖关系-信号处于正交相位，可以看出，如果灵敏度在高频（蓝色）增加，则在低频时减小（红色） ） 使用依赖于频率的压缩可以提高所有频率的灵敏度。因此，我们从概念上解决了降低所有频率的量子噪声的问题，问题仍然是：如何实现这种频率依赖性。 为此，您需要弄清楚如何将压缩的相位转换为压缩的幅度。 实际上，这非常简单：产生相移：
$$ display $$ E_ {f} ^ {sqz} = E_0 e ^ {-2r} \ sin（\ phi）\ rightarrow E_0 e ^ {-2r} \ sin（\ phi + \ pi / 2）= E_ { a} e ^ {-2r} $$显示$$
通常，一个简单的反射镜足以移动相位，这将改变光行进的路径的长度。 但是，在这种情况下，您需要一种能够产生与频率相关的相移的设备：不要在高频下移相，而在低频下移相
$ inline $ \ pi / 2 $ inline $ 。
当前，在未来的探测器的所有设计中创建依赖于频率的压缩的主要概念是使用附加的滤波谐振器。 如果压缩的真空在从谐振频率失谐时从这种谐振器反射回来，它将获得必要的频率依赖性。 但是，这具有很大的困难：为了建立所需的频率依赖性，谐振器必须在真空中长几百米，这非常昂贵并且难以控制。 我们有另一个想法。
事实是，在检测器本身中已经有许多尺寸合适，损耗低并且具有众所周知的控制方法的谐振器，但是它们不能直接使用-对于依赖于频率的压缩，必须使谐振失谐。 但是每个谐振器都有许多谐振频率，而检测器只能在其中之一上工作。 这个想法是使用
不同的共振，反射来自干涉仪本身的挤压光，以获得必要的频率依赖性。 问题仍然存在：如何使用在与激光器的主要工作频率不同的频率上产生的频率依赖性。 然后量子纠缠得以解救。
4.量子纠缠与EPR悖论
纠缠性质的问题无疑值得单独撰写。 我
在上一篇有关Habré的
文章中讨论了更多
复杂性 ，因此在这里我仅简要描述其主要属性。 让我们从
EPR悖论 （爱因斯坦-波多尔斯基-罗森）开始：三位先生注意到量子力学中有一个陷阱。 一方面，存在不确定性原理，即不可能同时精确地测量粒子的坐标和动量（在我们的情况下是光的振幅和相位）。 另一方面，可以做一个简单的实验：以粒子衰变为例，其中诞生了两个相同的粒子。 根据动量守恒定律，它们将以相同的速度向相反的方向散射。 如果我们测量一个粒子的动量，我们将确切知道第二个粒子的动量。 如果我们测量第二个粒子的坐标，我们将同时知道坐标（我们测量了它）和动量（我们从第一个粒子的测量中预测了它），由于不确定性关系，这似乎是不可能的。 通过引入粒子纠缠的概念来解决可见的矛盾：两个粒子不是彼此独立的，它们由一个波动函数来描述。 该波动函数是非局部的：在测量之前，无法说出哪个粒子朝哪个方向飞行。 从某种意义上说，它们都同时沿两个方向飞行，并且仅在测量时才随机选择要测量的颗粒。 它们的坐标和动量是关联的，因此不确定性关系不适用于它们的相对值。 此外，如果一个粒子（例如）受到某种力的作用，则第二个粒子也会“感觉”到该力-它的测量参数将相应变化。
因此，对我们来说最重要的事情是：如果我们有两个粒子，则可以通过测量第一个粒子来准确地预测第二个粒子的属性。 我们可以将影响源置于一个粒子的路径上，它会立即作用于两个粒子。 进行正确的测量后，我们可以看到这种效果的结果。
我们如何使用它（《自然物理学》 [2]中的文章首次提出）。 粒子在EPR中的作用是由两个压缩真空束以两个频率发挥的：干涉仪的基本频率和谐振器的下一个谐振频率。 我们将它们弄混了，其中之一（高频）会从调谐谐振器反射并进行测量。 他得到了频率依赖性。 由于光线被缠结，因此频率相关性也以基频传输到光束。 测量后，我们可以理想地以理想的精度预测主光束中的信号。 为此，我们分别在两个单独的检测器上进行测量，并以最佳方式处理数据。
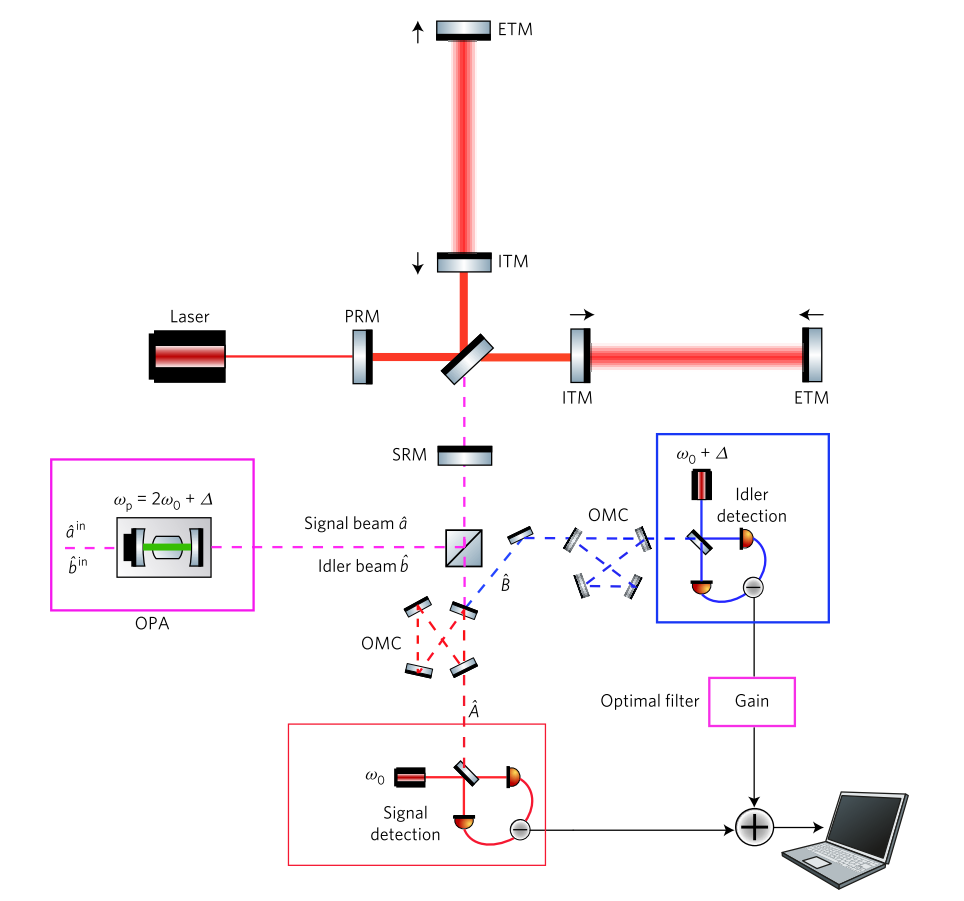一种基于[2]中纠缠的完整的频率相关压缩方案。 OPA（光学参量放大器）以不同的频率产生两个纠缠的压缩真空束，这两个束都被发送到检测器。 载频的光束在干涉仪中谐振。 高频光束从较高的谐振之一失谐。 在输出处，将射线分离并在两个不同的零差检测器上进行检测，然后以最佳方式对其进行处理。5.实验
我们的实验不包括带有运动镜的完整干涉仪。 相反，我们正在探索使用从谐振器反射的纠缠光来获得频率相关压缩的可能性。
简化的实验设计。 我们没有一个完整的干涉仪，而是使用一个2.5m长的光学谐振器。 代替两个不同的零差探测器，我们使用一个探测器，但使用两个不同频率的参考光束。就像我在上面写的那样，在干涉仪中，辐射压力产生了被挤压光的频率依赖性，这破坏了探测器的灵敏度。 为了消除这种频率依赖性，我们需要创建被压缩光的逆频率依赖性。 在我们的实验中，灵敏度不会破坏辐射压力（我们没有移动反射镜），但会破坏检测器与共振的失谐（请参见下图（a））。 在信号正交（相位读数）中进行测量时，这会破坏低频（红色）下的灵敏度。
为了恢复灵敏度，我们从相反方向的共振中重建了一条额外的光线（惰轮）。 然后经过测量，我们可以完全恢复灵敏度。 在EPR方面-我们可以预测使用量子纠缠光以更高的精度测量相位正交的结果。
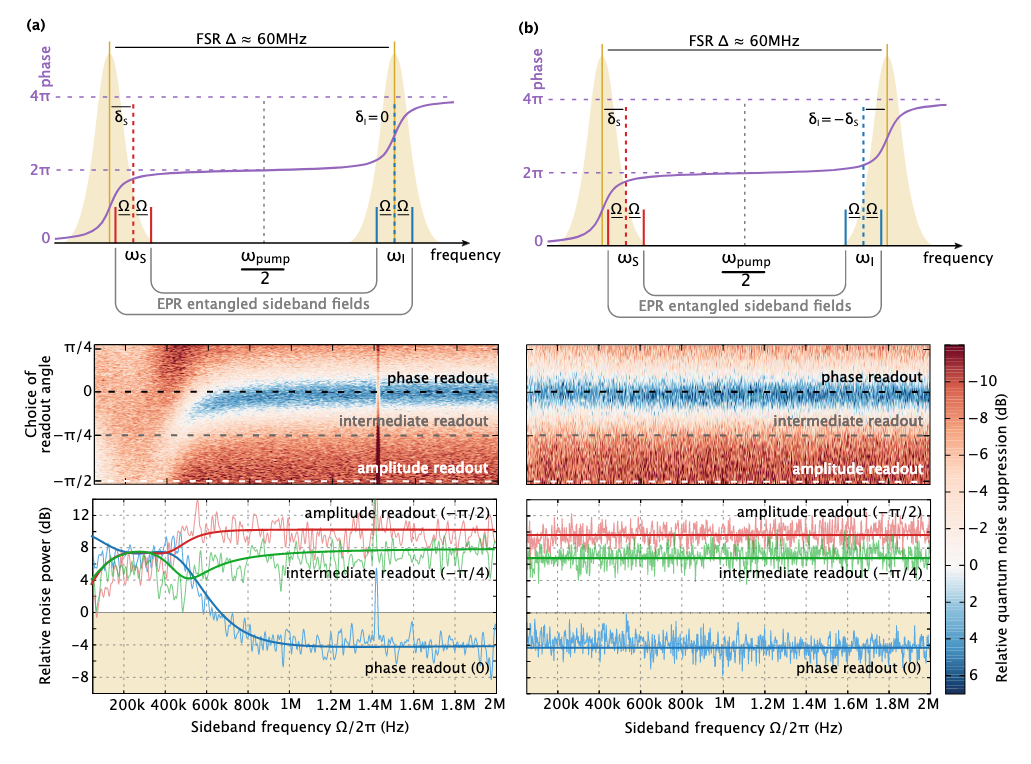两个实验观察与频率有关的压缩。 在第一个（a）中，我们从检测器的谐振中调谐了信号束，从而破坏了相位正交的灵敏度（并创建了被压缩光的频率依赖性）。 在第二个实验中，我们创建了第二个射线（惰轮）的附加频率依赖性，由于两个射线之间的量子纠缠，信号和ilder能够通过消除在第一个实验中引入的频率依赖性来恢复受损的灵敏度。在上图中，（a）中的频率相关性非常模糊。 这是由于后期处理的局限性：理想情况下，需要两个单独的零差检测器，可以对这些信号进行最佳滤波。 但是，在另一种模式下，如果我们从一个方向的共振中重建两条光线，则可以获得被压缩光的良好频率依赖性。 这样的方案与检测器无关，但是给出了安装选项的想法。 好吧，只是美丽的实验数据:)
6.结论
总结一下。 在所有现代和未来的探测器中，光的量子涨落都是主要且最基本的噪声源。 为了抑制它们，可以使用量子相关性-压缩光。 但是，为了减少检测器的整个频率范围内的噪声，有必要压缩低频处的振幅波动和高频处的相位波动。 建议使用特殊的滤波谐振器进行这种依赖于频率的压缩。 传统上，这种谐振器非常昂贵并且难以实现。 我们的替代方法是将检测器本身用作量子谐振光的滤波器谐振器。 我们做了一个实验，证明了量子纠缠实际上可以实现这个想法。
approach，这种方法不是万能药：您必须为方便而付费。 为了使该概念充分发挥作用，有必要使用两个零差探测器，这在实验上是相当困难的。 另外，第二个检测器增加了灵敏度的噪声-尽管比压缩获得的噪声小得多。
在这项工作中，我们研究了错综复杂的光线，并展示了如何使用它们来提高未来探测器的灵敏度。 但这当然只是在真实探测器中实施此方法的漫长道路上的第一步：您需要检查在真实干涉仪，移动镜，两个零差等情况下一切正常。 总的来说，工作仍然很忙。
对于那些对细节感兴趣的人，
请参阅我们的文章以及首次提出该想法的
文章 [2]。
[1] S. Hild
超越第二代GW检测器[2]
Y. Ma等人，关于通过EPR纠缠超出标准量子极限的引力波检测的提案，《自然物理学》第13卷，第776–780页（2017年）7.杂项
现在有关LIGO的一些新闻：
- 目前，LIGO在O3工作周期的最后六个月中已注册了26个事件。 可以在https://gracedb.ligo.org/superevents/public/O3/上监视事件，并且有用于iPhone的完整应用程序 。
- 最有趣的也许是最近发生的事件 ，它可能检测到黑洞和中子星的融合。 例如，您可以阅读N +1或《 科学美国人》 。 , .
- 100 . , (c 55 130 ). , , .
- LIGO , , , . . LIGO . , , . , , , , .
: , , : @hbar_universe .