线性回归及其恢复方法

资料来源： xkcd

线性回归是与数据分析相关的许多领域的基本算法之一。 原因很明显。 这是一种非常简单易懂的算法，促成了其数十年（甚至数百年）的广泛使用。 这个想法是，我们假设一个变量对一组其他变量具有线性依赖性，然后尝试恢复这种依赖性。

但是本文不是关于应用线性回归来解决实际问题。 在这里，我们将讨论在使用Apache Ignite编写机器学习模块时遇到的分布式算法实现恢复的有趣功能。 一些基本的数学知识，机器学习的基础知识和分布式计算将帮助您弄清楚如何恢复线性回归，即使数据分布在数千个节点上也是如此。

你在说什么

我们面临着恢复线性相关性的任务。 作为输入，给出了许多假设独立变量的向量，每个向量都与因变量的某个值相关联。 这些数据可以用两个矩阵的形式表示：

$$

$$\开始{pmatrix} a_ {11}＆a_ {12}＆a_ {13}＆...＆a_ {1n} \\ a_ {21}＆a_ {22}＆a_ {23}＆...＆ a_ {2n} \\ ... \\ a_ {m1}＆a_ {m2}＆a_ {m3}＆...＆a_ {mn} \\ \结束{pmatrix} \开始{pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \结束{pmatrix}$$

现在，由于假设了相关性，并且除了它是线性的，我们还以矩阵乘积的形式写我们的假设（为简化此处和以下的表示法，假设方程的自由项 $$$x_n$ ，以及矩阵的最后一列 $$包含单位）：

$$

$$\开始{pmatrix} a_ {11}＆a_ {12}＆a_ {13}＆...＆a_ {1n} \\ a_ {21}＆a_ {22}＆a_ {23}＆...＆ a_ {2n} \\ ... \\ a_ {m1}＆a_ {m2}＆a_ {m3}＆...＆a_ {mn} \\ \结束{pmatrix} \次\开始{pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \结束{pmatrix} = \开始{pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \结束{pmatrix}$$

与线性方程组非常相似，对吧？ 看来，但最有可能不会出现这种方程组的解决方案。 其原因是几乎所有真实数据中都存在噪声。 同样，其原因可能是缺乏线性关系，您可以通过引入非线性依赖于源的其他变量来尝试解决该关系。 考虑以下示例：

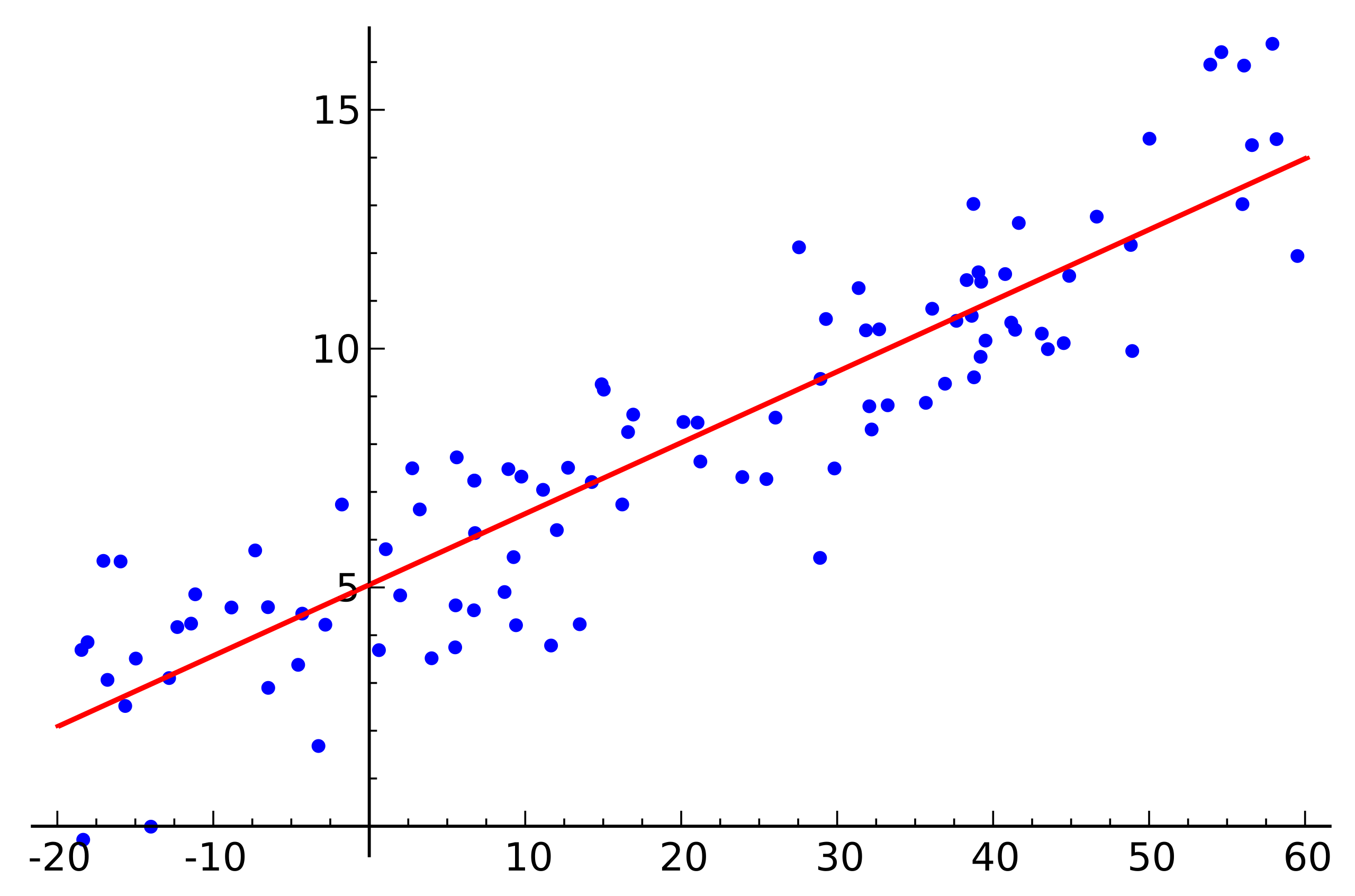资料来源： 维基百科

这是一个简单的线性回归示例，显示了一个变量（沿轴 $$$y$ ）来自另一个变量（沿轴） $$$x$ ） 为了使与本示例相对应的线性方程组具有解，所有点都必须恰好位于一条直线上。 但是事实并非如此。 但是，它们并不是仅仅由于噪声（或者因为存在线性相关性的假设是错误的）而位于一条直线上。 因此，为了从实际数据恢复线性相关性，通常必须引入另一个假设：输入数据包含噪声，并且此噪声具有正态分布 。 可以对其他类型的噪声分布进行假设，但是在大多数情况下，正态分布将在后面讨论。

最大似然法

因此，我们假设存在随机正态分布的噪声。 在这种情况下怎么办？ 对于这种情况，在数学中存在并且被广泛使用的最大似然法 。 简而言之，其本质在于似然函数的选择及其随后的最大化。

我们回到从具有正常噪声的数据中恢复线性相关性的过程。 注意，假定的线性关系是数学上的期望 $$$\亩$ 可用正态分布。 同时， $$$\亩$ 假定一个或另一个值，取决于可观察到的事物 $$$x$ ，如下所示：

$$

$$P（\ mu \ mid X，\ sigma ^ 2）= \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {-\ frac {（x- \ mu）^ 2} {2 \ sigma ^ 2}}}$$

我们现在代替 $$$\亩$ 和 $$$X$ 我们需要的变量：

$$

$$P（x \ mid A，B，\ sigma ^ 2）= \ prod_ {i \ in [1，m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {-\ frac {（b_i-a_ix）^ 2} {2 \ sigma ^ 2}}}，A中的a_i \，B中的b_i$$

它仍然只是找到向量 $$$x$ 在这个概率最大的时候。 要最大化此类功能，首先进行对数会很方便（该功能的对数将在与功能本身相同的位置达到最大值）：

$$

$$f（x）= ln（\ prod_ {i \ in [1，m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {-\ frac {（b_i-a_ix ）^ 2} {2 \ sigma ^ 2}}}）= \ sum_ {i \ in [1，m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} \; -\ sum_ {i \ in [1，m]} \ frac {（b_i-a_ix）^ 2} {2 \ sigma ^ 2}$$

反过来，归结为最小化以下功能：

$$

$$f（x）= \ sum_ {i \ in [1，m]}}（b_i-a_ix）^ 2$$

顺便说一下，这称为最小二乘法。 通常，上述所有推理都被省略，并且仅使用此方法。

QR分解

如果找到该函数的斜率等于零的点，则可以找到上述函数的最小值。 渐变将写为：

$$

$$\ nabla f（x）= \ sum_ {i \ in [1，m]} 2a_i（a_ix-b_i）= 0$$

QR分解是一种矩阵方法，用于解决最小二乘法中使用的最小化问题。 在这方面，我们以矩阵形式重写方程式：

$$

$$A ^ T A x = A ^ Tb$$

所以，我们布置矩阵 $$在矩阵上 $$$Q$ 和 $$$R$ 并执行一系列转换（此处将不考虑QR分解算法本身，仅考虑与任务相关的QR分解算法）：

$$

$$\ begin {align}＆（QR）^ T（QR）x =（QR）^ Tb; \\＆R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \结束{align}$$

矩阵 $$$Q$ 是正交的。 这使我们摆脱了工作。 $$$Q Q ^ T$ ：

$$

$$\ begin {align}＆R ^ T R x = R ^ T Q ^ T b; \\＆（R ^ T）^ {-1} R ^ T R x =（R ^ T）^ {-1} R ^ T Q ^ T b; \\＆R x = Q ^ T b。 \结束{align}$$

如果您更换 $$$Q ^ T b$ 在 $$$z$ 事实证明 $$$R x = z$ 。 鉴于 $$$R$ 是上三角矩阵，看起来像这样：

$$

$$\开始{pmatrix} r_ {11}＆r_ {12}＆r_ {13}＆r_ {14}＆...＆r_ {1n} \\ 0＆r_ {22}＆r_ {23}＆r_ { 24}＆...＆r_ {2n} \\ 0＆0＆r_ {33}＆r_ {34}＆...＆r_ {3n} \\ 0＆0＆0＆r_ {44}＆.. 。＆r_ {4n} \\ ... \\ 0＆0＆0＆0＆...＆r_ {nn} \\ \结束{pmatrix} \次\开始{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \开始{pmatrix} z​​_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$$

这可以通过替代方法解决。 项 $$$x_n$ 就像 $$$z_n / r_ {nn}$ 上一项 $$$x_ {n-1}$ 就像 $$$（z_ {n-1}-r_ {n-1，n} x_n）/ r_ {n-1，n-1}$ 等等。

在这里值得注意的是，通过使用QR分解所得到的算法的复杂性是 $$$O（200万^ 2）$ 。 此外，尽管矩阵乘法运算已很好地并行化，但无法编写此算法的有效分布式版本。

梯度下降

说到最小化某个函数，总是值得回顾一下（随机）梯度下降的方法。 这是一种简单有效的最小化方法，该方法基于迭代计算某个点处函数的梯度，然后将其移至与梯度相反的一侧。 每个这样的步骤将解决方案减至最少。 渐变看起来相同：

$$

$$\ nabla f（x）= \ sum_ {i \ in [1，m]} 2a_i（a_ix-b_i）$$

由于梯度算子的线性特性，该方法也很好地并行化和分布。 请注意，在上式中，独立的术语位于总和的符号下。 换句话说，我们可以为所有指标独立计算梯度 $$$我$ 从第一到 $$$k$ ，与此同时，使用 $$$k + 1$ 之前 $$$m$ 。 然后添加所得的渐变。 相加的结果将与我们立即计算从第一个索引到第一个索引的梯度相同 $$$m$ 。 因此，如果数据分布在数据的多个部分之间，则可以在每个部分上独立地计算梯度，然后可以将这些计算的结果相加以获得最终结果：

$$

$$\ nabla f（x）= \ sum_ {i \ in P_1} 2a_i（a_ix-b_i）+ \ sum_ {i \ in P_2} 2a_i（a_ix-b_i）+ ... + \ sum_ {i \ in P_k} 2a_i（a_ix-b_i）$$

在实现方面，这适合MapReduce范例。 在梯度下降的每个步骤中，将用于计算梯度的任务发送到每个数据节点，然后将计算出的梯度收集在一起，并使用它们求和的结果来改善结果。

尽管实现简单并且可以在MapReduce范例中执行，但梯度下降也有其缺点。 特别是，与其他更专业的方法相比，实现收敛所需的步骤数要大得多。

低速QR

LSQR是解决问题的另一种方法，它既适用于重建线性回归，也适用于求解线性方程组。 它的主要特征是它结合了矩阵方法和迭代方法的优点。 在SciPy库和MATLAB中都可以找到此方法的实现。 在此将不给出此方法的描述（可以在LSQR文章中找到：稀疏线性方程式和稀疏最小二乘法的算法 ）。 取而代之的是，将演示一种使LSQR适应分布式环境中执行的方法。

LSQR方法基于双角化程序 。 这是一个迭代过程，其每次迭代都包含以下步骤：


但基于事实，矩阵 $$进行水平分区，则每次迭代可以表示为MapReduce的两个步骤。 因此，可以在每次迭代期间最小化数据传输（仅长度等于未知数的向量）：



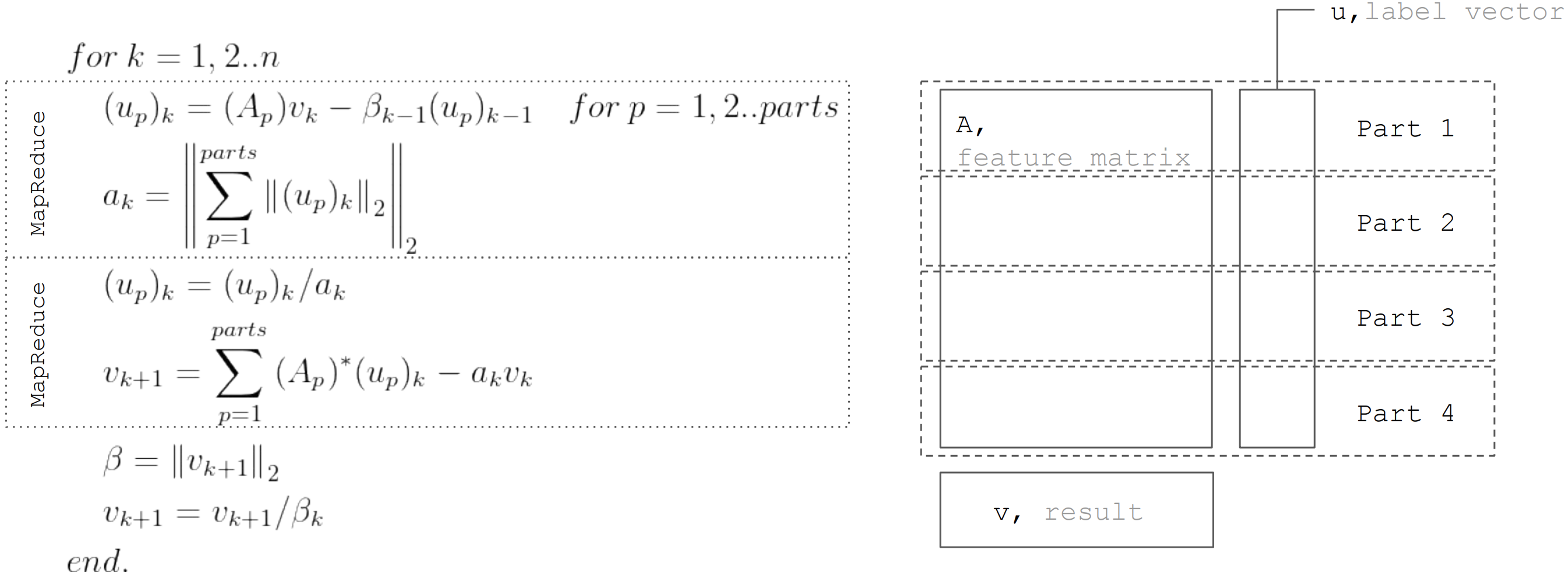
在Apache Ignite ML中实现线性回归时使用此方法。

结论

线性回归恢复算法有很多，但并非所有算法都可以在任何条件下应用。 因此，QR分解非常适合在小型数据阵列上进行精确求解。 梯度下降法很容易实现，可让您快速找到一个近似解。 LSQR结合了前两种算法的最佳性能，因为它可以分布，并且与梯度下降相比收敛更快，并且与QR分解不同，它还可以使算法尽早停止以找到近似解。