
在任何社交网络中,最有价值的资源之一就是“友谊图”-通过此列中的连接传播信息,将有趣的内容发送给用户,并将建设性的反馈发送给内容作者。 此外,图形还是重要的信息来源,可让您更好地了解用户并不断改善服务。 但是,在图形增长的那些情况下,从技术上提取信息在技术上越来越困难。 在本文中,我们将讨论OK.ru中用于处理大型图形的一些技巧。
首先,请考虑一个来自现实世界的简单任务:确定用户的年龄。 知道年龄可以使社交网络选择更多相关内容并更好地适应人。 在社交网络上创建页面时,似乎已经表明了年龄,但实际上,用户经常会狡猾,并指出与实际年龄不同的年龄。 社交图谱可以帮助纠正这种情况:)。
以鲍勃(Bob)为例(文章中的所有字符都是虚构的,与现实的任何巧合都是随机房子创造力的结果):

一方面,鲍勃的朋友中有一半是青少年,这表明鲍勃也是青少年。 但是他也有老朋友,所以对答案的信心很低。 来自社交图谱的其他信息可以帮助阐明答案:

不仅考虑鲍勃直接参与的活动,还考虑了他的朋友之间的活动,我们可以看到鲍勃是青少年社区的一员,这使我们可以更加自信地得出他的年龄结论。
这种数据结构被称为自我网络或自我子图;长期以来,它已成功用于解决许多问题:搜索社区,识别漫游器和垃圾邮件,来自好友和内容的推荐等。 但是,为具有数亿个节点和数百亿弧的图中的所有用户计算子图的自我的过程充满了许多“小技术难题” :)。
主要问题是,当考虑图形中有关“第二步”的信息时,连接数将发生二次爆炸。 例如,对于具有150个直接自我链接的用户,子图最多可以包含 链接,对于拥有5,000个朋友的活跃用户,自我子图可以增长到超过1200万个链接。
另一个复杂的事实是该图存储在分布式环境中,并且没有节点在内存中具有该图的完整映像。 在学院和行业中都进行平衡图分区的工作,但是即使在收集自我子图时获得最高的结果也会导致“所有人共享”的交流:为了获得有关用户朋友的朋友的信息,您将必须转到所有“分区”。在大多数情况下。
在这种情况下,一种可行的替代方法是强制数据复制(例如Google的文章中的算法3),但是这种复制也不是免费的。 让我们尝试找出在此过程中可以改进的地方。
天真的算法
首先,请考虑用于生成自我子图的“朴素”算法:

该算法假定原始图被存储为邻接表,即 有关用户所有朋友的信息存储在单个记录中,键中包含用户ID,值中包含朋友ID列表。 为了执行第二步并获取有关朋友的信息,您需要:
- 将图形转换为边列表,其中每个边都是单独的条目。
- 使边列表自身相连,这将在长度为2的图形中给出所有路径。
- 按路径开始分组。
在每个用户的输出中,我们获得每个用户的长度为2的路径列表。 在这里应该注意,结果结构实际上是用户的两步式邻域 ,而自我子图是其子集。 因此,要完成此过程,我们需要过滤掉直交朋友之外的所有弧。
该算法很好,因为它是在Apache Spark下在Scala的两行中实现的。 但是优势不止于此:对于工业规模的图表而言,网络通信的数量已超出限制,并且运行时间以天为单位。 主要困难是由我们进行合并和分组时发生的两个随机操作造成的。 是否可以减少发送的数据量?
自我子图在一个洗牌
鉴于我们的友谊图是对称的,您可以使用Tomas Schank提出的优化方法:
- 您可以不加入而获得所有长度为2的路径-如果Bob拥有朋友Alice和Harry,那么就有Alice-Bob-Harry和Harry-Bob-Alice路径。
- 分组时,入口处的两条路径对应于同一条新边。 路径Bob-Alice-Dave和Bob-Dave-Alice包含与Bob相同的信息,这意味着您只能发送第二条路径,并按用户ID对其进行排序。
应用优化后,工作方案将如下所示:

- 在生成的第一阶段,我们获得了长度为2的路径列表,其中包含订单ID过滤器。
- 第二,我们在路上按第一个用户分组。
在这种设置下,该算法完成一次混洗操作,并且通过网络传输的数据大小减半。 :)
在内存中布置自我子图
我们尚未考虑的重要问题是如何将子图的自我中的数据分解为内存。 为了存储整个图,我们使用了邻接表。 这种结构对于需要从整体上完成成品图的任务很方便,但是如果我们要从各个部分构建一个图并进行更细微的分析,则该结构将非常昂贵。 我们任务的理想结构应有效执行以下操作:
- 从不同分区获得的两个图的并集。
- 得到所有人类朋友。
- 检查是否连接了两个人。
- 存储在内存中,无需装箱。
满足这些要求的最合适的格式之一是稀疏CSR矩阵的模拟:
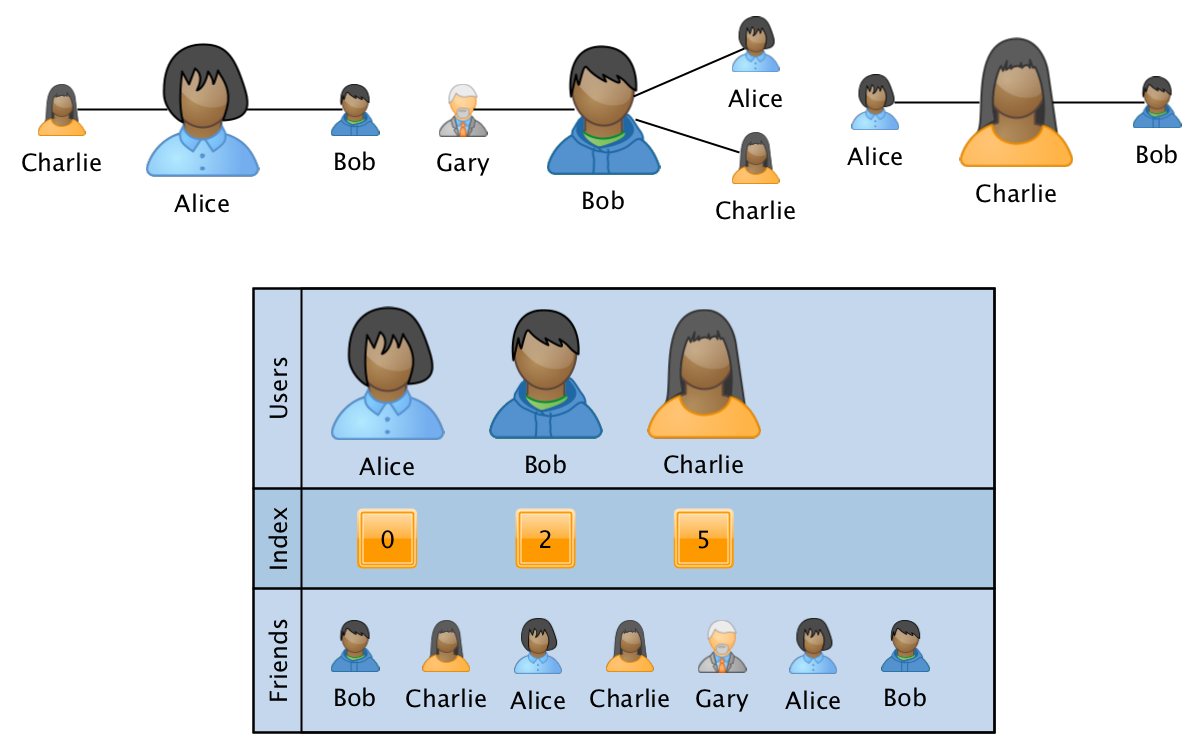
在这种情况下,图形以三个数组的形式存储:
- users-一个排序的数组,其中包含参与图形的所有用户的ID。
- index-与用户大小相同的数组,其中为每个用户存储一个指向第三数组中有关用户关系信息开头的索引指针。
- 朋友-大小等于数组边数的数组,其中依次为用户的相应ID显示相关用户的ID。 在有关单个用户链接的信息内,将数组排序以提高处理速度。
在这种格式中,合并两个图的操作是在线性时间内执行的,并且每个顶点数量的对数获取有关特定用户或一对用户的信息的操作。 在这种情况下,内存的开销不取决于图形的大小,因为使用了固定数目的数组。 通过添加大小等于朋友大小的第四个数据数组,可以在图形中保存与关系相关的其他信息。
使用图对称性,您只能存储“上三角”弧的一半(当弧仅从较小的ID到较大的ID存储),但是在这种情况下,单个用户的所有连接的重建将花费线性时间。 在这种情况下,一个很好的折衷方法可能是使用“上三角”编码进行节点之间的存储和传输,以及在将子图的自我加载到内存中进行分析时使用对称编码。
减少洗牌
但是,即使执行了上述所有优化之后,构造所有自我子图的任务仍然会花费很长时间。 在我们的例子中,集群的利用率很高,大约需要6个小时。 仔细研究表明,复杂性的主要来源仍然是混洗操作,而混洗中涉及的数据的很大一部分将在接下来的阶段中丢弃。 事实是,所描述的方法为每个用户建立了一个完整的两步式邻域,而自我子图只是该邻域的一个相对较小的子集,仅包含内部弧。
例如,如果通过与鲍勃的直接邻居哈利和弗兰克交往,我们知道他们不是彼此的朋友,那么我们已经可以在第一步中过滤掉此类外部路径。 但是为了找出所有Gary和Frenkov是否是朋友,您将不得不将友谊图拖到所有计算节点的内存中,或者在处理每条记录时进行远程调用,根据任务的条件,这是不可能的。
尽管如此,如果我们在很小的情况下允许自己发现友谊而实际上却不存在,那就有解决方案。 整个系列的概率数据结构可以将数据存储期间的内存消耗减少几个数量级,同时允许一定数量的错误。 这种类型最著名的结构是Bloom过滤器 ,该过滤器已在工业数据库中成功使用多年,以补偿“长尾”缓存中的遗漏。
Bloom过滤器的主要任务是回答以下问题:“此元素是否包含在许多以前见过的元素中?” 此外,如果过滤器回答“否”,则该元素可能不包含在集合中,但如果回答“是”,则该元素仍不存在的可能性很小。
在我们的例子中,“元素”将是一对用户,而“集合”将是图形的所有边。 然后可以成功应用Bloom过滤器以减少随机播放的大小:

预先准备好有关图表信息的Bloom过滤器后,我们可以查看Harry的朋友,发现Bob和Ilona不是朋友,这意味着我们不需要向Bob发送有关Gary和Ilona之间的联系的信息。 但是,仍然必须发送有关Harry和Bob自己是朋友的信息,以便Bob分组后可以完全恢复他的友谊。
去除混洗
应用过滤器后,发送的数据量减少了约80%,并且任务在1小时内完成了中等的群集负载,使您可以自由地并行执行其他任务。 在这种模式下,它已经可以“投入运行”并每天使用,但仍有优化的潜力。
听起来很矛盾,但是如果您允许自己犯一定比例的错误,就可以解决问题而无需重新洗牌。 布隆过滤器可以帮助我们:

如果使用过滤器查看Bob的朋友列表,我们几乎可以确定 Alice和Charlie是朋友,我们可以立即将相应的弧添加到Bob的自我子图中。 在这种情况下,整个过程将花费不到15分钟的时间,并且不需要通过网络进行数据传输,但是实际上,取决于过滤器设置,可能没有一定比例的电弧。
过滤器添加的额外电弧不会对某些任务造成明显的失真:例如,在计算三角形时,我们可以轻松地校正结果,而在为机器学习算法准备属性时,则可以在下一步中学习ML校正。
但是在某些任务中,额外的电弧会导致结果质量的严重恶化:例如,当使用远程自我(没有用户的顶点)在自我子图中搜索连接的组件时,组件之间的“幻影桥”的概率相对于其大小呈二次方增长,从而导致几乎在所有地方我们都有一个重要组成部分。
有一个中间区域,需要通过实验评估额外电弧的负面影响:例如,某些社区搜索算法可以非常成功地应对少量噪声,返回几乎相同的社区结构。
而不是结论
自我用户子图是OK积极使用的重要信息来源,以提高建议的质量,完善人口统计信息和打击垃圾邮件,但它们的计算存在许多困难。
在本文中,我们研究了为社交网络的所有用户构建自我子图的任务方法的演变,并且能够将工作时间从最初的20小时缩短为1小时,并且在错误率很小的情况下,可以将工作时间缩短至10-15分钟。
最终决定所依据的三个“支柱”是:
- 使用图对称属性和Tomas Schank算法。
- 使用稀疏CSR矩阵有效地存储自我子图。
- 使用布隆过滤器减少网络上的数据传输。
可以在Zeppelin笔记本中找到有关算法代码如何演变的示例。