成长。 重量 三个邻居

在寻找一个有趣且简单的数据集时，我遇到了这个英俊的男人 。

关于这个美女

它包含了10,000名男女的生长和体重的数据。 没有说明。 没有什么“多余的”。 仅高度，重量和地面标记。 我喜欢这种神秘的简单性。

好吧，让我们开始吧！

对我来说有趣的是什么？

• 大多数男人和女人的体重和身高范围是多少？
• 他们是什么样的 “普通”男人和“普通”女人？
• 简单的KNN机器学习模型可以根据这些数据预测身高体重吗？

走吧

初看

首先，加载必要的模块

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

当库完全站起来时-是时候加载DataSet本身并查看前10个元素。 这是必要的，以便使我们的内心平静，并正确装载了所有东西。

顺便说一句，不要惊慌，身高和体重与我们以前的有所不同。 这是因为测量系统不同： 英寸和磅 ，而不是厘米和千克 。

 data = pd.read_csv('weight-height.csv') data.head(10) 

好啊 我们看到前十个条目是“男人”。 我们看到他们的身高和体重 。 数据加载良好。

现在，您可以查看集合中的行数。

 data.shape >> (10000, 3) 

万行 /记录。 并且每个都有三个参数 。 你需要什么！

现在该修复测量系统了。 现在这里是厘米和千克。

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

现在，它变得越来越熟悉。 最早的记录告诉我们，一个男人的身高约为190厘米，体重约为110公斤。 大个子 我们叫他鲍勃。

但是如何理解：与其他相比，它是很多还是一点？ 我们可能都是正负豆吗？ 这是稍后。

现在，让我们找出该数据集中的两种性别对称性如何 ？

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

理想情况下，均分。 这样做很好，因为如果有：9999个男人和1个女人，那么就不会假装此DataSet可以很好地揭示两个性别。 就我们而言，一切正常！

分开学习！

现在的直觉表明，分开两个性别并分别进行探索是正确的。 确实，在生活中我们经常看到男人和女人的身高和体重正负不同

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

让我们看一下pandas模块为我们提供的少量描述性统计信息。

男子 ：

 data_male.describe() 

女人 ：

 data_female.describe() 

我们发现男性的平均身高和中位数分别为175厘米和85公斤。 而女性 ：162厘米和62公斤。 这告诉我们没有强排放物。 或者它们在中位数的两侧对称。 这是非常罕见的。

但是，两性均数与中位数之间存在细微偏差。 但是它们微不足道，仅在百分之一的位置可见。 让我们继续前进！

直方图

此图按增长顺序从最小值到最大值建立值，并显示单个实例的数量。

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

数据呈钟形分布。 非常类似于正态分布 。

除了用于正态分布的统计检验之外，还有视觉检验。 如果按类型和逻辑分布似乎是正常的-我们可以假设我们正在处理它。

可以进行统计正态性检验并确定p值，但是 我不能 这超出了本文的范围。

学习用笔工作

熊猫对我们来说很重要。 但是您至少需要自己计算一次统计数据。 现在，我将展示如何计算标准偏差 。

让我们以男人和成长为特征的例子来做。

平均值

配方

$$

$$M = \ frac {1} {N} \ sum \ limits_ {i = 1} ^ N n_i$$

在哪里

• M-平均值
• N是实例数
• ni-单实例

代码：

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

平均身高-175cm

偏差平方

$$

$$d_i =（n_i-M）^ 2$$

在哪里

• 双单偏差
• ni-单实例
• M-平均

代码：

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

分散度

配方

$$

$$D = \ frac {1} {N} \ sum \ limits_ {i = 1} ^ N d_i$$

在哪里

• D是色散值
• 双单偏差
• N是实例数

代码：

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

分散度-53

标准偏差

配方

$$

$$std = \ sqrt {D}$$

在哪里

• std-标准偏差值
• D是色散值

代码：

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

标准差-7

置信区间

现在，我们将找出68％，95％和99.7％的男性和女性的增长和体重范围 。

这并不是那么困难-您需要从平均值中减去标准差。 看起来像这样：

• 68％ -正负一标准偏差
• 95％ -正负两个标准偏差
• 99.7％ -正负三个标准差

我们编写了一个辅助函数，将考虑以下内容：

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

好吧，将其应用于数据：

男装 | 成长性

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

男装 | 机重

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

妇女 | 成长性

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

妇女 | 机重

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

因此得出结论：

• 大多数男人：154厘米-197厘米和58公斤-112公斤。
• 大多数女性：141厘米-182厘米和36公斤-87公斤。

现在只剩下将机器学习应用于此集合并尝试按身高预测体重。

最近的邻居

“到最近的邻居”算法很简单。 它用于分类任务-区分猫和狗-以及回归任务-根据身高猜测体重。 这就是我们所需要的！

为了进行回归，他使用以下算法：

• 记住所有数据点
• 当出现新点时，它搜索K的最近邻居（数字K由用户设置）
• 平均结果
• 给出答案

首先，您需要将数据集划分为训练和测试部分并测试算法

对男人进行实验

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

分开了，该尝试了。

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

我们不会走远，在三个邻居处停下来。 但是问题是：这样的模型能猜出我的体重吗？

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg非常接近。 这第二，我的体重是89.8kg

男性预测图

建立我最喜欢的科学部分的时间是图形。

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

妇女的模型和预测图

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

当然，有趣的是这些图看起来如何：

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

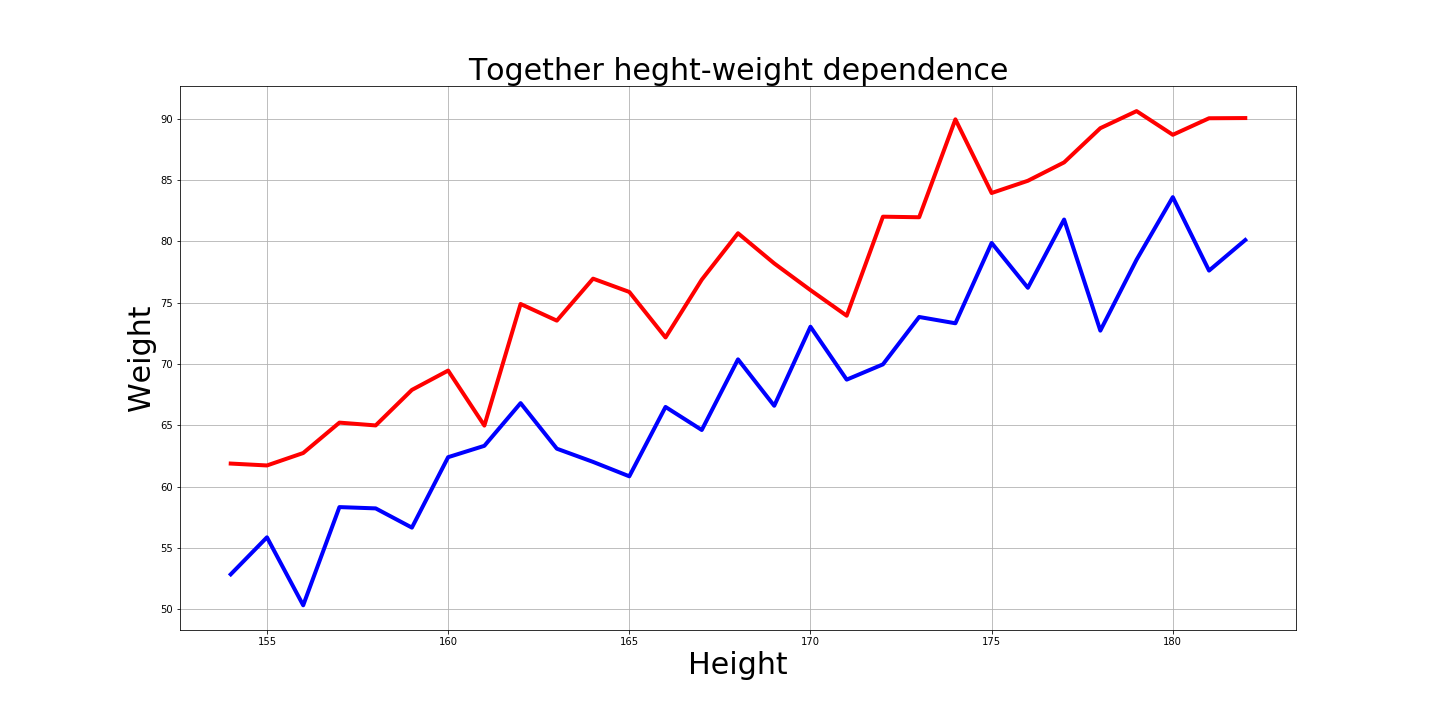
问题答案

-大多数男人和女人的体重和身高范围是多少？

99.7％的男性：从154厘米到197厘米，从58公斤到112公斤。
99.7％的女性：从141厘米到182厘米，从36公斤到87公斤。

-他们是什么样的“普通”男人和“普通”女人？

平均每个人是175厘米和85公斤。
而平均女性是162cm和62kg。

-根据这些数据，简单的KNN机器学习模型会按身高预测体重吗？

是的，模型预测的体重为88公斤，而我的体重为89.8公斤。

我所做的一切，我都收集在这里

文章的缺点

• 没有对DataSet的描述。 人们的年龄和其他因素可能有所不同。 因此，请您不要出于信仰而接受，而是为了进行实验。
• 以一种好的方式-有必要对分布的正态性进行测试

结语

就像您达到99.7％的间隔