“如果您在大象的笼子上看到题词“水牛”，请不要相信自己的眼睛。” Kozma Prutkov

在上一篇有关面向模型的设计的文章中 ，它说明了为什么需要一个对象模型，并且证明了如果没有这种对象模型，则只能将基于模型的设计作为营销的暴风雪，毫无意义和残酷地谈论。 但是，当出现对象模型时，胜任的工程师始终会提出一个合理的问题：有什么证据表明对象的数学模型与真实对象相对应。

关于电驱动器的面向模型设计的文章中给出了对此问题的一个答案示例。 在本文中，我们将考虑为航空空调系统创建模型的示例，并通过一些理论上的一般性考虑来稀释实践。

创建对象的可靠模型。 理论

为了避免麻烦，我将立即向您介绍有关为面向模型的设计创建模型的算法。 它只有三个简单步骤：

步骤1.开发描述代数系统动态行为的代数-微分方程组。 如果您了解过程的物理原理，这很简单。 许多科学家已经为我们开发了牛顿，布伦努利，纳维耶·斯托克斯和其他罗盘和拉比诺维奇Shtangels名称的基本物理定律。

步骤2.在结果系统中，隔离可以从测试中获得的一组经验系数和模拟对象的特征。

步骤3.对对象进行测试，并根据野外实验的结果调整模型，使其与实际情况相符，并具有必要的详细程度。

如您所见，只有两个三。

实际例子

飞机中的空调系统（SCR）连接到自动压力维护系统。 飞机中的压力应始终大于外部压力，而压力的变化率应使飞行员和乘客不会流鼻血。 因此，空气的流入和流出的控制系统对于安全性是重要的，并且昂贵的测试系统已经在其开发中投入使用。 它们会产生飞行高度的温度和压力，在不同高度的机场重现起飞和着陆的模式。 开发和调试硬通货控制系统的问题正在发挥其全部潜力。 我们将驾驶测试台多长时间才能获得满意的控制系统？ 显然，如果将控制模型调整为对象模型，则可以大大减少测试台架上的工作周期。

航空空调系统由与任何其他热力系统相同的热交换器组成。 电池-在非洲也是电池，只有空调。 但是由于起飞质量和飞行器尺寸的限制，热交换器被制造得尽可能紧凑和尽可能高效，以便从下部质量传递尽可能多的热量。 结果，几何形状变得非常奇怪。 例如在考虑中的情况。 图1显示了一种板式换热器，其中在板之间使用膜来改善热传递。 冷热冷却剂在通道中交替流动，而流动方向为横向。 一种冷却剂供应到正面切口，另一种冷却剂供应到侧面。

为了解决SCR控制问题，我们需要知道在这样的热交换器中每单位时间有多少热量从一种介质传递到另一种介质。 温度的变化率取决于此，我们对此进行调节。

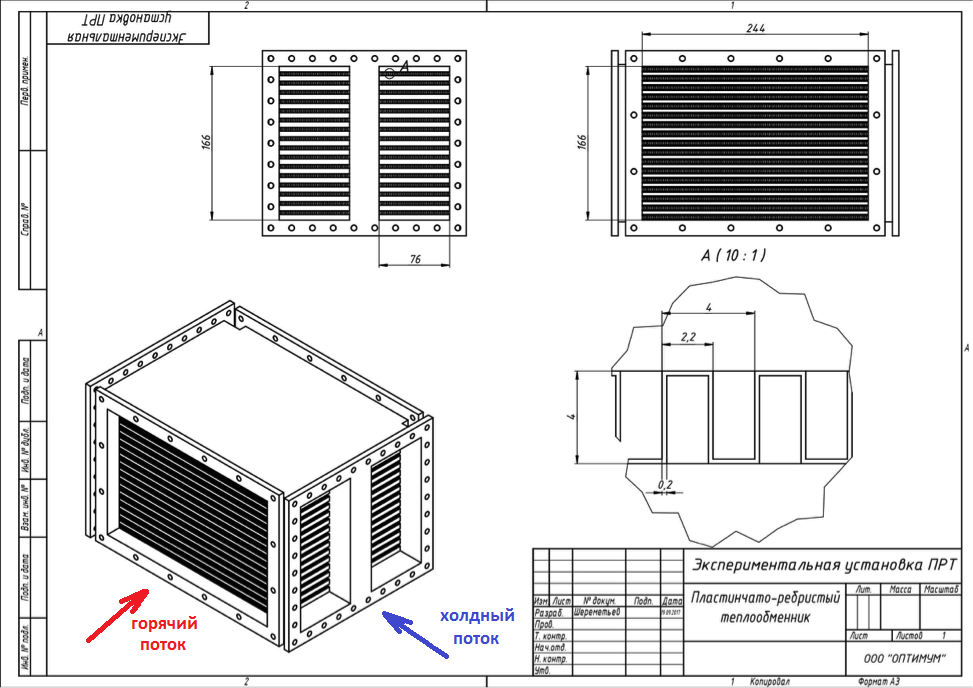
图1.飞机热交换器示意图。

建模问题。 液压件

乍看之下，任务非常简单，有必要计算通过热交换器通道的质量流量以及通道之间的热量。
通道中冷却剂的质量流率使用伯努利公式计算：

其中：
ΔP是两点之间的压降；
ξ是冷却液的摩擦系数；
L是通道的长度；
d是通道的水力直径；
ρ是冷却液的密度；
ω是通道中的冷却剂速度。

对于任意形状的通道，水力直径通过以下公式计算：

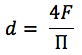
其中：
F是孔的面积；
P-湿通道周长。

摩擦系数根据经验公式计算，并取决于流速和冷却液的特性。 对于不同的几何形状，将获得不同的依存关系，例如，光滑管道中的湍流公式：

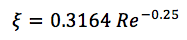
其中：
Re是雷诺数。

对于扁平通道中的流量，可以使用以下公式：

根据伯努利公式，您可以计算给定速度下的压降，反之亦然，根据给定压降计算通道中冷却剂的速度。

传热

冷却剂和壁之间的热流由以下公式计算：

其中：
α[W /（m2×度）]-传热系数；
F是孔的面积。

对于冷却剂在管道中的流动问题，已经进行了足够的研究，并且有许多计算方法，通常，对于传热系数α[W /（m2×deg）]，这全都取决于经验。

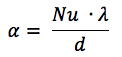
其中：
Nu是Nusselt数，
λ是液体的热导率[W /（m×deg）]
d是液压（等效）直径。

经验标准依赖性用于计算Nusselt数（标准），例如，用于计算圆管Nusselt数的公式如下所示：

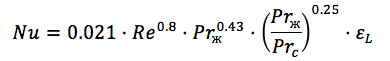
在这里，我们已经看到了雷诺数，壁温和流体温度下的普朗特数以及不均匀系数。 （ 来源 ）

对于波纹板式换热器，公式类似（ 来源 ）：

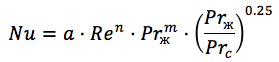
其中：
对于湍流，n = 0.73 m = 0.43，
系数α-在0.065和0.6之间变化，具体取决于塔板数和流动方式。

注意，仅针对流中的一个点计算此系数。 对于下一点，我们有一个不同的液体温度（它已经变热或变冷），一个不同的壁温，因此，所有的雷诺数和普朗特数都是浮动的。

在这一点上，任何数学家都会说不可能精确计算系数变化10次的系统，他是正确的。

任何实践的工程师都会说，每个热交换器在制造上都是不同的，不可能计算系统，这也是正确的。

但是面向模型的设计呢？ 全部都消失了吗？

在这里，西方软件的高级销售商将为您提供一台超级计算机和3D计算系统，例如“不带任何方式”。 而且您需要运行一天的计算才能获得1分钟的温度分布。

显然，这不是我们的选择，我们需要调试控制系统，如果不是实时的，那么至少在可预见的将来。

戳法

制造了热交换器，进行了一系列测试，并且在给定的流量下设置了稳态温度效率表。 简单，快速，可靠，就像从测试中获得的数据一样。

这种方法的缺点是对象没有动态特性。 是的，我们知道稳态热通量是多少，但是我们不知道从一种运行模式切换到另一种运行模式时会建立多长时间。

因此，在计算了必要的特性之后，我们在测试期间直接设置了控制系统，这是我们从一开始就希望避免的。

面向模型的方法

要创建动态热交换器模型，必须使用测试数据，以消除经验计算公式中的不确定性-努塞尔数和水力阻力。

决定很简单，就像所有的创造力一样。 我们采用经验公式，进行实验并确定系数a的值，从而消除了公式中的不确定性。

一旦我们有了一定的传热系数值，所有其他参数都由守恒的基本物理定律确定。 温度差和热传递系数决定了每单位时间传递到通道的能量。

知道了能量流，就可以解决液压通道中冷却剂的能量质量和动量守恒方程。 例如，这：

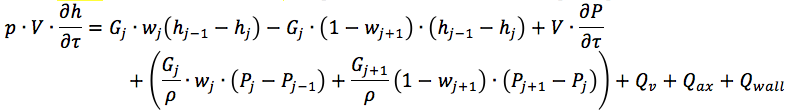
对于我们的情况，壁和冷却剂之间的热通量-Qwall-尚未确定。 更多细节可以在这里找到...

还有通道壁的温度导数方程：

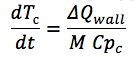
其中：
ΔQwall-通道壁的入流与出流之差；
M是通道壁的质量；
C _pc是壁材料的热容。

模型精度

如上所述，在热交换器中，我们在板表面上具有温度分布。 对于稳态值，可以取板的平均值并将其使用，将整个热交换器表示为一个集中点，在该集中点，在相同的温差下，热交换器的整个表面都会发生热传递。 但是对于瞬态模式，这种近似可能不起作用。 另一个极端是获得数十万个点并加载超级计算机，这也不适合我们，因为任务是实时或更快速地配置控制系统。

问题出现了，您需要断开热交换器多少个部分才能获得可接受的精度和计算速度？

一如既往，我手头有一个胺热交换器的模型。 热交换器是管子，载热体在管子中流动，并在凹坑之间被加热。 为了简化任务，可以将热交换器的整个管子表示为一条等效管，而将管子本身表示为一组离散的设计单元，在每个单元中计算出一个传热的点模型。 单电池的模型图如图2所示。热空气通道和冷空气通道通过壁连接，该壁在通道之间提供热传递。

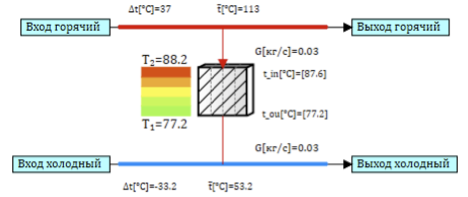
图2.换热器单元模型。

管状热交换器模型易于定制。 您只能更改一个参数-沿管道长度的截面数，并查看不同分区的计算结果。 我们将计算几个选项，从分为5个点的长度（图3）到多达100个点的长度（图4）开始。

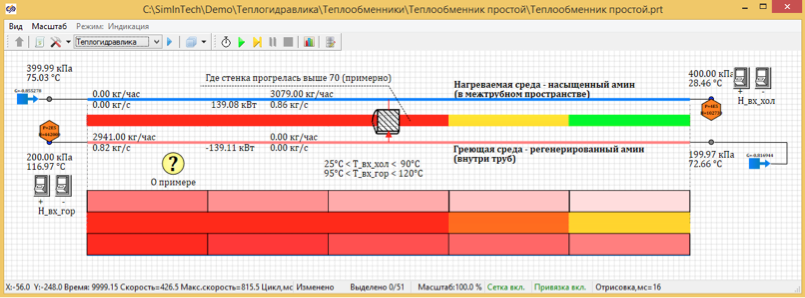
图3. 5个设计点的固定温度分布。

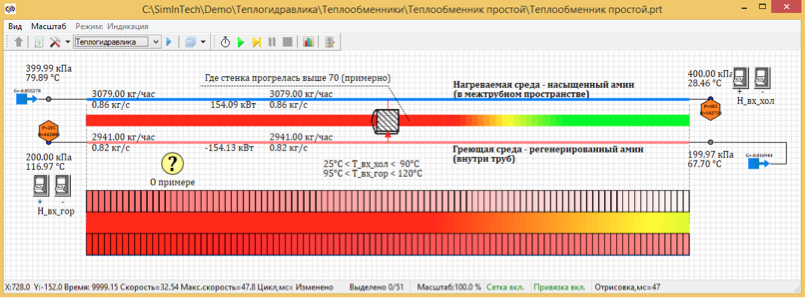
图4. 100个设计点的固定温度分布。

计算结果表明，稳态温度除以100点时为67.7度。 并且当划分为5个计算点时，温度为72、66摄氏度。

而且，相对于实时的计算速度显示在窗口的下部。
让我们看看稳态温度和计算速度如何随设计点数而变化。 在具有不同数量的计算单元的计算中，稳态温度的差异可用于评估结果的准确性。

表1.温度和计算速度对沿热交换器长度的设计点数的依赖性。

分析此表，我们可以得出以下结论：

• 计算速度与换热器模型中的设计点数成比例地降低。
• 计算精度的变化呈指数变化。 随着点数的增加，每个后续增加处的细化都会减少。

如图1所示，在带有错流式热载体的板式换热器中，从基本设计单元创建等效模型会有些复杂。 我们需要以组织错流的方式连接单元。 对于4个单元，电路外观如图5所示。

冷却剂流沿热和冷支路分为两个通道，这些通道将通过热结构连接，因此，冷却剂在通过通道时会与不同的通道进行热交换。 模拟错流，热载热体在每个通道中从左向右流动（见图5），与自下而上的冷载热体通道依次进行热交换（见图5）。 最热的点在左上角，因为热载体与冷通道中已经加热的冷却剂进行热交换。 右下角最冷的地方，冷的冷却液与已经在第一部分冷却的热的冷却液进行热交换。

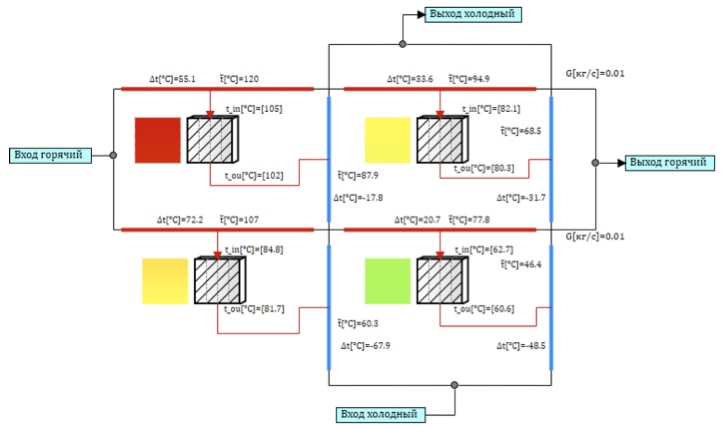
图5. 4个设计单元的错流模型。

用于板式热交换器的这种模型没有考虑由于热导率引起的电池之间的热传递，并且没有考虑冷却剂的混合，因为每个通道都是绝缘的。

但是在我们的情况下，后一种限制不会降低精度，因为在热交换器的设计中，波纹膜将流沿着冷却剂分成许多隔离的通道（见图1）。 让我们看看用增加设计单元数的板式换热器进行建模时，计算精度会如何。

为了进行准确性分析，我们使用两个选项将热交换器划分为设计单元：

1. 每个方形单元包含两个液压（冷热流）和一个热敏元件。 （见图5）
2. 每个方形单元包含六个液压元件（热和冷流中的三个部分）和三个热元件。

在后一种情况下，我们使用两种类型的连接：

• 冷热气流的逆流；
• 相关的冷热流。

与横流相比，迎面而来的电流提高了效率，并且相关电流降低了。 对于大量的像元，会发生流量平均，并且一切都变得接近其周围的实际横向流量（请参见图6）。

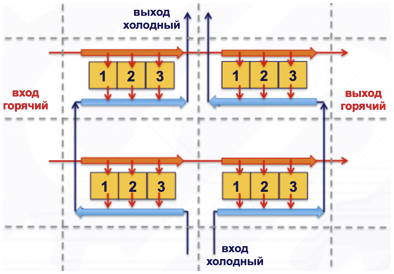
图6.带有3个元素的四个单元的错流模型。

图7显示了沿热线供应温度为150°C，沿冷线供应温度为21°C的空气时，换热器中稳态稳态温度分布的结果，用于划分模型的各种选项。 电池上的颜色和数字反映了电池中的平均壁温。

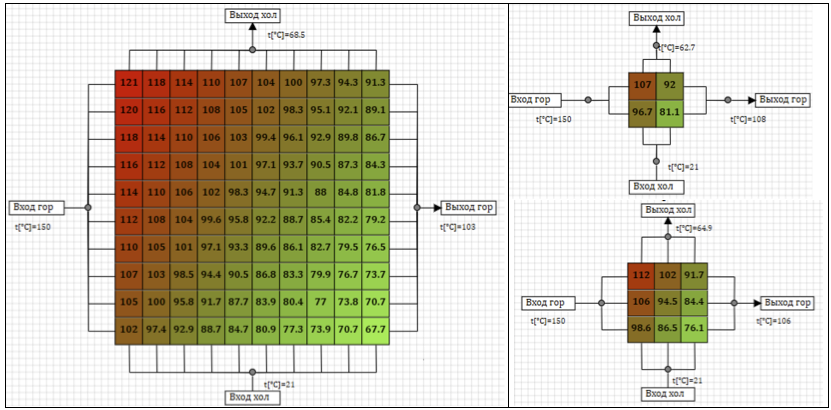
图7.不同计算方案的稳态温度。

表2显示了热交换器后的加热空气的稳态温度，具体取决于热交换器模型划分成的单元。

表2.温度取决于热交换器中设计单元的数量。

随着模型中计算单元数量的增加，最终稳态温度也随之增加。 可以将不同分区的稳态温度之间的差异视为计算精度的指标。 可以看出，随着计算单元数量的增加，温度趋于极限，并且精度的提高与计算点的数量不成比例。

问题出现了，但是我们需要什么模型的准确性？

这个问题的答案取决于我们模型的目的。 由于本文是关于面向模型的设计的，因此我们将创建一个模型来调整控制系统。 这意味着模型的精度必须与系统中使用的传感器的精度相当。

在我们的案例中，温度是通过热电偶测量的，精度为±2.5°C。 任何用于调整控制系统的更高精度都是没有用的，我们真正的控制系统只是“看不到”。 因此，如果我们假设无限数量的分区的极限温度为70°C，那么给我们提供超过67.5°C的温度的模型将具有足够的精度。 在计算单元格中具有3点的所有模型和在单元格中具有1点的模型都大于5x5。 （表2中以绿色突出显示）

动态运行模式

为了评估动态模式，我们针对各种设计方案评估了换热器壁最热和最冷点的温度变化过程。 （见图8）


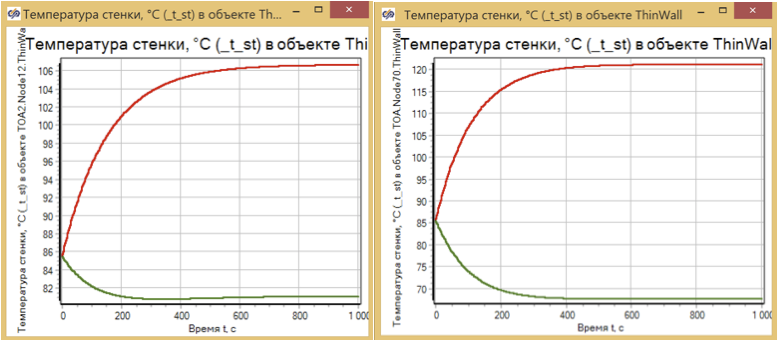
图8.热交换器预热。 尺寸为2x2和10x10的模型。

可以看出，过渡过程的时间及其性质实际上不取决于计算出的晶胞数量，而仅取决于加热金属的质量。

因此，我们得出结论，对于SCR控制系统所需的精度，在20至150°C的模式下进行换热器的真实模拟，大约需要10-20个计算点。

实验动态模型设置

, , , , , .

, , . 9 . , , , .

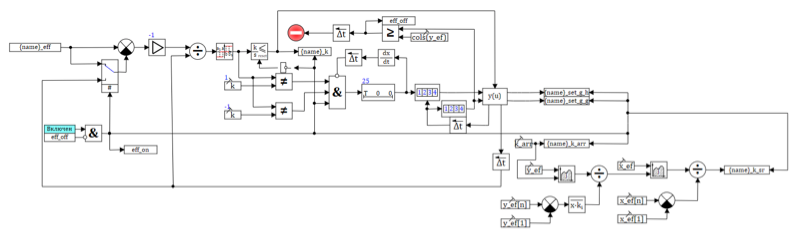
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
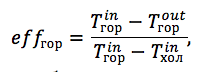
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

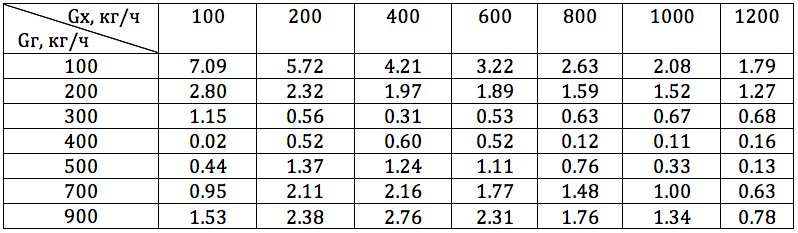
, 10 .

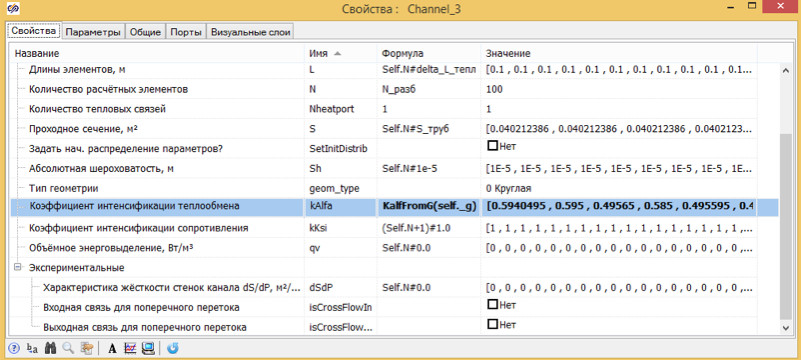
10. .

结论

• - .
  
• .
  
• .
  
• - !

. .