系列“白噪声画出一个黑色正方形”
这些出版物出版周期的历史始于
G.Sekey的书
《概率论与数理统计中的悖论》 (
第43页 ),发现了以下说法:

图 1。
根据分析,对第一个出版物(
第1部分 ,
第2部分 )的评论和随后的推理已经使以更直观的形式呈现该定理的想法变得成熟。
由于二项式概率分布和许多相关定律,大多数社区成员都熟悉Pascal三角形。 为了了解Pascal三角形的形成机理,我们将通过其形成流程的展开来更详细地扩展它。 在帕斯卡三角形中,节点由0和1的比率组成,如下图所示。
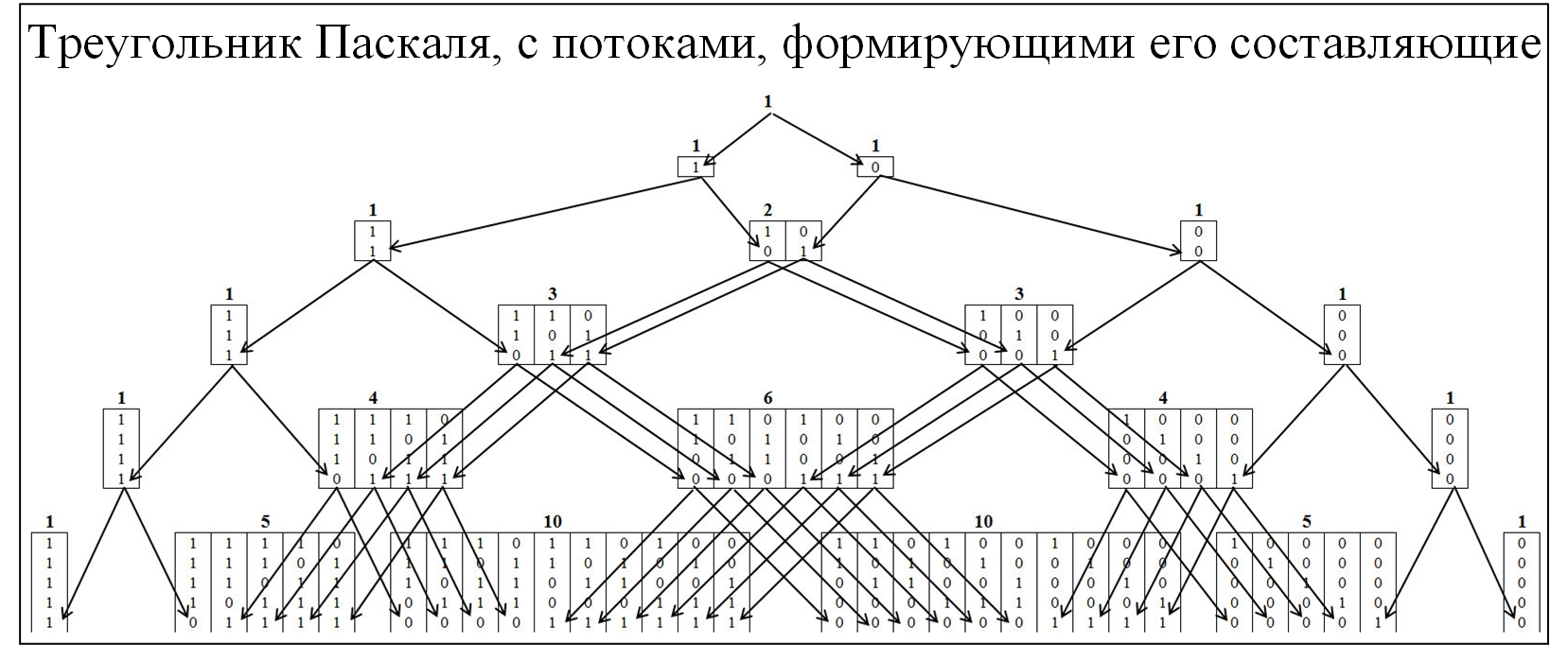
图 2。
为了理解Erds-Renyi定理,我们将组成一个类似的模型,但是节点将由存在最大链的值构成,这些链依次由相同的值组成。 聚类将根据以下规则进行:链01/10,聚类为“ 1”; 链00/11,聚类为“ 2”; 链000/111,聚类为“ 3”,依此类推。 在这种情况下,我们将金字塔分解为两个对称的组件,如图3所示。

图 3。
引起您注意的第一件事是,所有运动都是从较低的簇到较高的簇发生的,反之亦然。 这是自然的,因为如果形成了大小为j的链,则它不再消失。
确定数字集中的算法后,我们设法获得以下递归公式,其重现机制如图4-6所示。
表示数字集中的元素,其中n是数字中的字符数(位数),最大链的长度为m。 并且每个元素将接收索引n; mJ。
表示从n; mJ传递到n + 1; m + 1J,n; mjn + 1; m + 1的元素数。

图 4。
图4显示,对于第一个集群,确定每一行的值并不困难。 并且这种依赖性等于:

图 5,
我们确定第二个簇,链长为m = 2,图6。
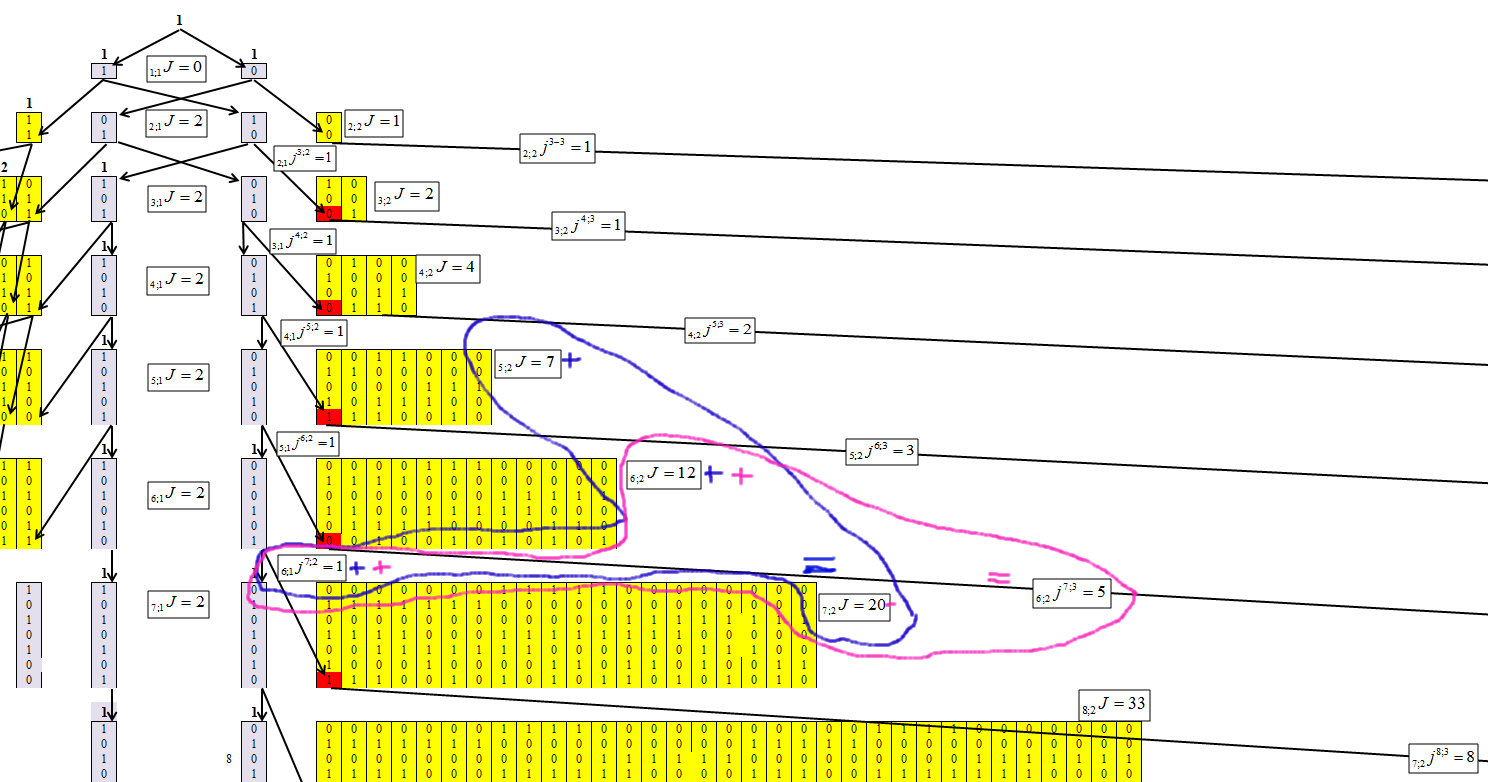
图 6。
图6显示,对于第二个集群,相关性等于:

图 7
我们确定第三个簇,链长为m = 3,图8。
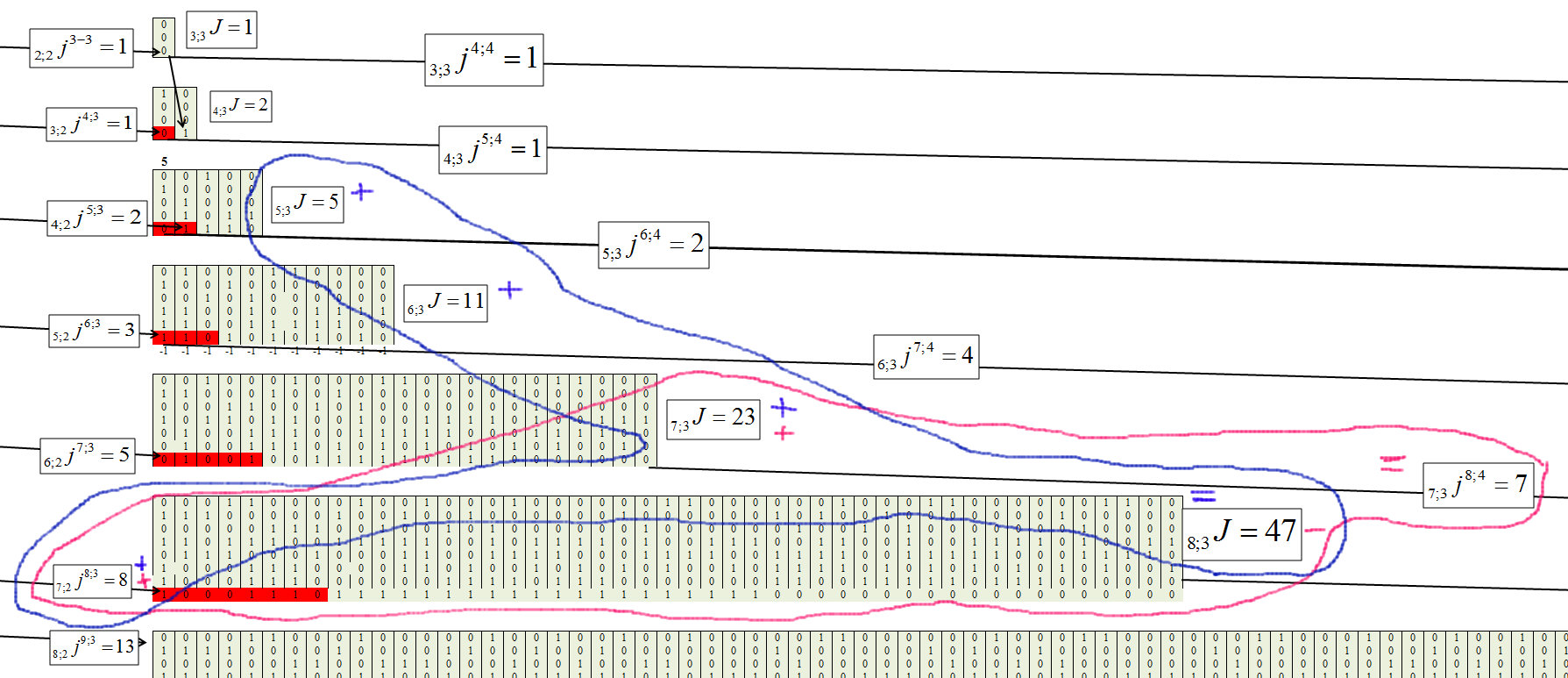
图 8。

图 9。
每个元素的通用公式采用以下形式:

图 10。

图 11。
验证码
为了进行验证,我们使用此序列的属性,如图12所示。该事实在于,从某个位置开始的行的最后一个成员对于行长增加的所有行取一个值。
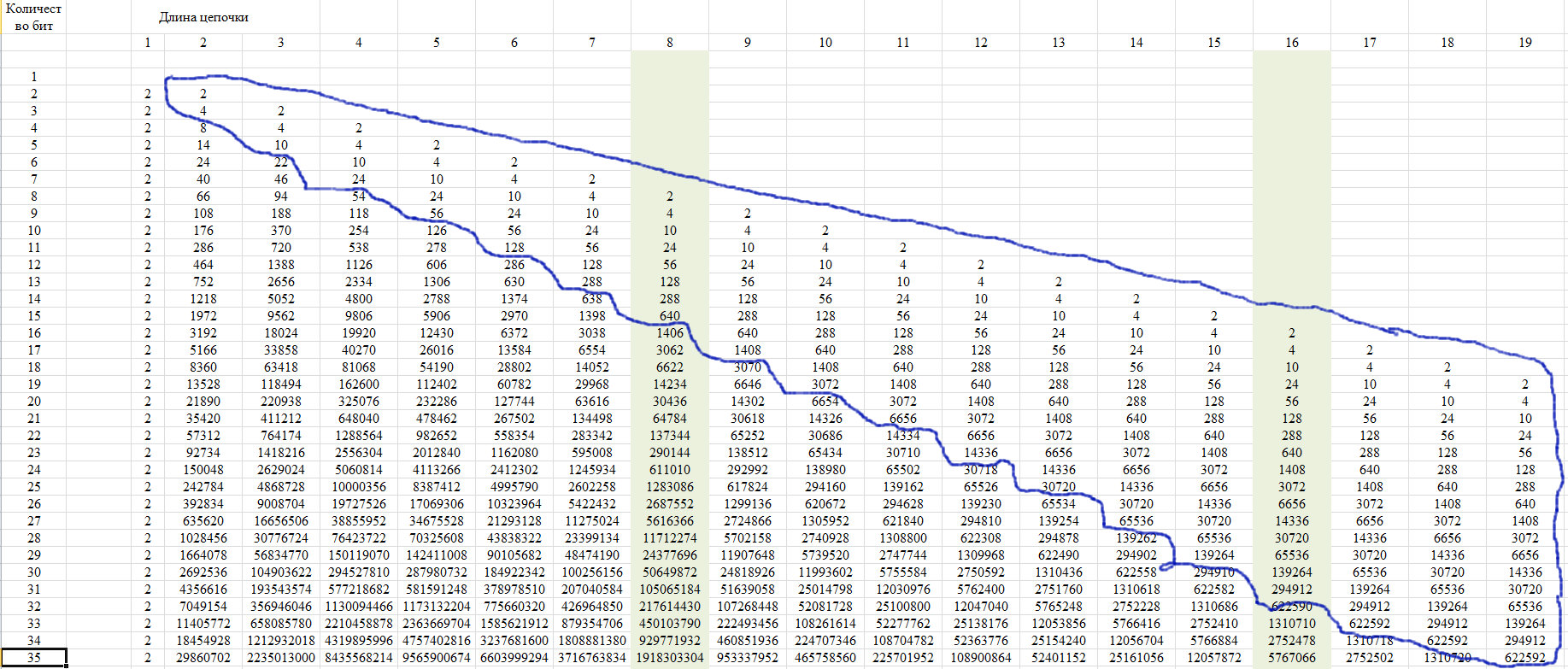
图 12
此属性是由于以下事实:如果链长超过整行的一半,则只有一条这样的链是可能的。 我们在图13的图中显示了这一点。

图 13
因此,对于k <n-2的值,我们得到以下公式:
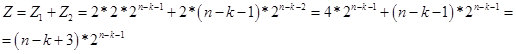
图 14。
实际上,Z的值是包含k个相同元素的链的数字的潜在数目(n位字符串中的选项)。 然后根据递归公式,确定k个相同元素链最大的数量(n位字符串中的选项)的数量。 现在,我假设Z值是虚拟的。 因此,在n / 2区域,它进入真实空间。 在图15中,带有计算的屏幕。

图 15
让我们显示一个256位字的示例,此算法可以确定该字。

图 16。
如果由GSPCH的可靠性为99.9%的标准确定,则256位密钥必须包含连续的字符相同的链,其字符数为5到17。也就是说,根据GSPCH的标准,这样才能满足具有99.9%的可靠性的随机相似性要求, GSPCH在2000年的测试中(以256位二进制数的形式发布结果)应仅给出最大序列长度相同值的结果:小于4或大于17。
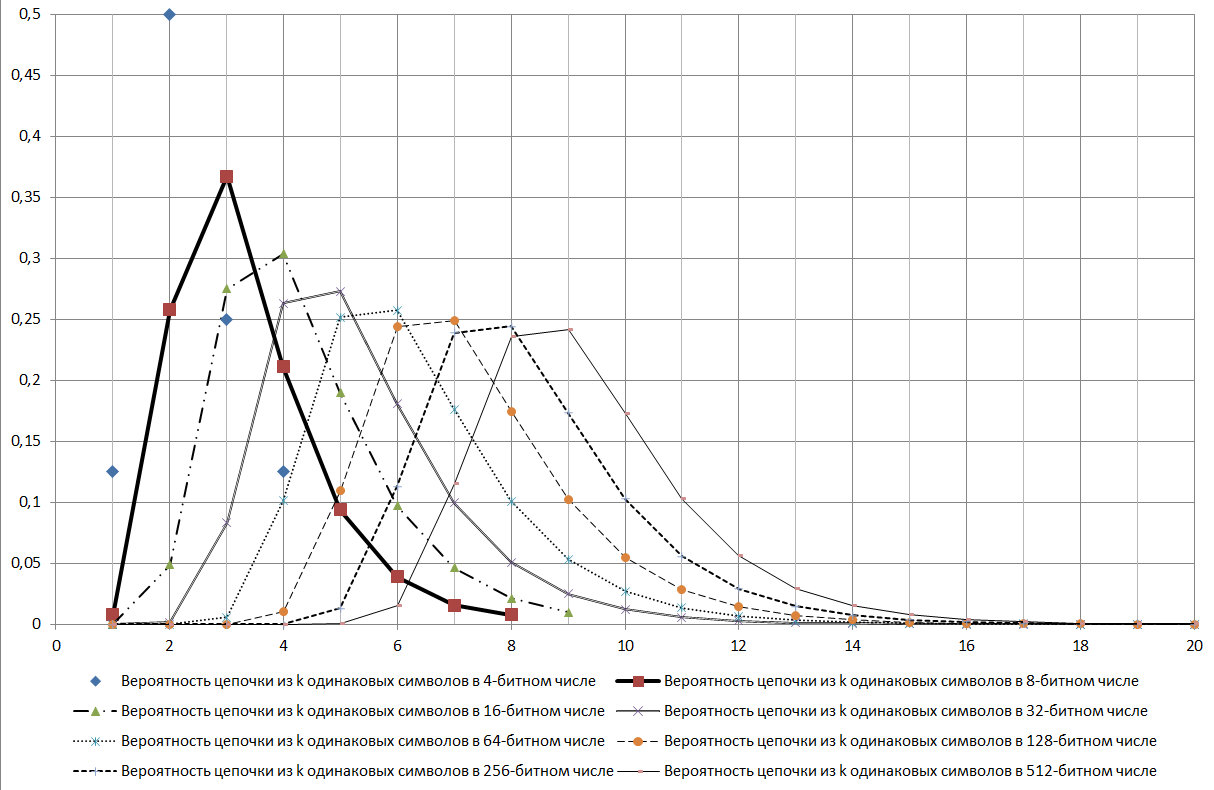
图 17。
从图17所示的图表可以看出,log2N链是正在考虑的分发方式。
在研究过程中,发现了该序列各种性质的许多迹象。 以下是其中一些:
- 应该通过卡方标准对其进行很好的测试;
- 给出分形特性存在的迹象;
- 可能是识别各种随机过程的良好标准。
还有更多其他联系。
在检查序列号
A006980的整数序列在线百科全书
(OEIS) (整数序列在线百科全书)中是否还存在这种序列时,请参考出版物
JL Yucas,计数二进制林登字的特殊集合Ars Combin。 ,第31卷(1991),第2页。 21-29 ,其中顺序显示在第28页(在表中)。 在出版物中,行的编号少了1,但值相同。 通常,该出版物是关于
Lyndon的
话的 ,也就是说,研究人员很可能甚至没有怀疑该系列与此方面有关。
让我们回到Erds-Renyi定理。 根据该出版物的结果,可以说,在给出的公式中,该定理是指一般情况,由Muavre-Laplace定理确定。 在这种表述中,所指示的定理不能成为级数随机性的明确标准。 但是分形,并且对于这种情况,表示可以将指定长度的链与更长的链组合在一起,不允许一个人明确地拒绝该定理,因为在配方中可能存在误差。 一个例子是这样的事实:如果对于一个数字的256位概率,其中最大8位链为0.244235,那么与其他更长的序列一起,一个数字中存在8位的概率已经是- 0.490234375。 也就是说,到目前为止,没有明确的机会拒绝这个定理。 但是该定理在另一个方面非常合适,这将在后面显示。
实际应用
让我们看一下VDG用户提供的示例:
“ ...神经元的树突分支可以表示为位序列。 当在任何位置激活突触链时,都会触发分支,然后触发整个神经元。 神经元的任务分别是不响应白噪声,据我所记得的Numenty,该链的最小长度是锥体神经元中具有其一万个突触的14个突触。 并根据公式得出:Log_ {2} 10000 = 13.287。 也就是说,由于自然噪声,将出现长度小于14的链,但不会激活神经元。 这是完全正确的 。
”我们将构建一个图形,但是考虑到Excel不会考虑大于2 ^ 1024的值这一事实,我们将限制自己的突触数量1023,并且考虑到这一点,我们将通过注释对结果进行插值,如图18所示。

图 18岁
当一个m = log2N = 11的链被编译时,有一个生物神经网络触发,该链是一个模态值,在0.78的情况下达到某种变化的阈值,概率。 并且错误的概率为1- 0.78 = 0.22。 假设有一个由9个传感器组成的链,确定事件的概率分别为0.37,则错误概率为1-0.37 = 0.63。 即,为了使错误概率从0.63降低到0.37,需要3.33个9元素链来工作。 11个元素和9个元素之间的差是2阶,即2 ^ 2 = 4倍,如果四舍五入为整数,则由于元素给出整数值,则3.33 =4。我们进一步希望减少处理8信号时的误差。元素,我们已经需要8个元素的11个触发链。 我想这是一种机制,使您可以评估情况并做出有关更改生物对象行为的决定。 我认为足够合理和有效。 考虑到我们了解自然界的事实,即它尽可能经济地使用资源,因此生物系统使用这种机制的假设是合理的。 而且,当我们训练神经网络时,实际上,我们减少了错误的可能性,因为为了完全消除错误,我们需要找到一种解析关系。
我们转向对数值数据的分析。 在数值数据分析中,我们尝试选择形式为y = f(xi)的分析依赖性。 在第一阶段,我们找到了她。 找到它之后,相对于回归方程式,我们可以将现有序列表示为二进制,其中我们将1分配给正值,将0分配给负值,然后分析一系列相同的元素。 我们确定沿着链长的最大短链分布。
接下来,我们转到Erdos-Renyi定理,由此得出,当进行大量的随机值检验时,必须在所生成数字的所有寄存器中形成一组相同的元素,即m = log2N。 现在,当我们检查数据时,我们不知道该系列的实际数量。 但是,如果您回头看,那么这个最大链给了我们理由,假设R是表征随机变量字段的参数,如图19所示。
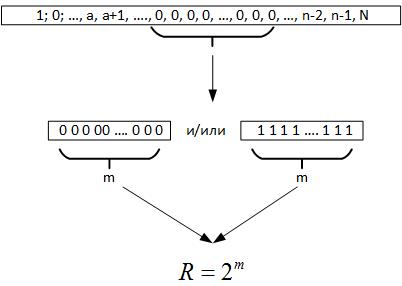
图 19
也就是说,比较R和N,我们可以得出以下结论:
- 如果R <N,则对历史数据重复几次随机过程。
- 如果R> N,则随机过程的维数大于可用数据,或者我们错误地确定了目标函数的方程。
然后,对于第一种情况,我们正在设计一个带有2 ^ m个传感器的神经网络,我想我们可以添加一对传感器来捕捉转变,并根据历史数据训练该网络。 如果训练后的网络无法学习,并且以50%的概率产生正确的结果,则意味着发现的目标函数是最优的,无法对其进行改进。 如果网络可以学习,那么我们将进一步改善分析依赖性。
如果序列的维数大于随机变量的维数,则可以使用随机变量的分形特性,因为任何大小为m的序列都包含所有较低维的子空间。 我想在这种情况下,有必要在除链m之外的所有数据上训练神经网络。
神经网络设计的另一种方法可能是预测期。
总之,必须说,在本出版物的出版过程中,发现了许多方面,其中随机变量的维数大小及其发现的属性与数据分析中的其他任务相交。 但是就目前而言,这些都是非常原始的形式,将留待将来的出版物使用。
上一部分:
第1 部分 ,
第2部分