正算术：克服自己领域中的浮点数。 第二部分

第一部分

4.数值系统的定量比较

4.1。 小数精度

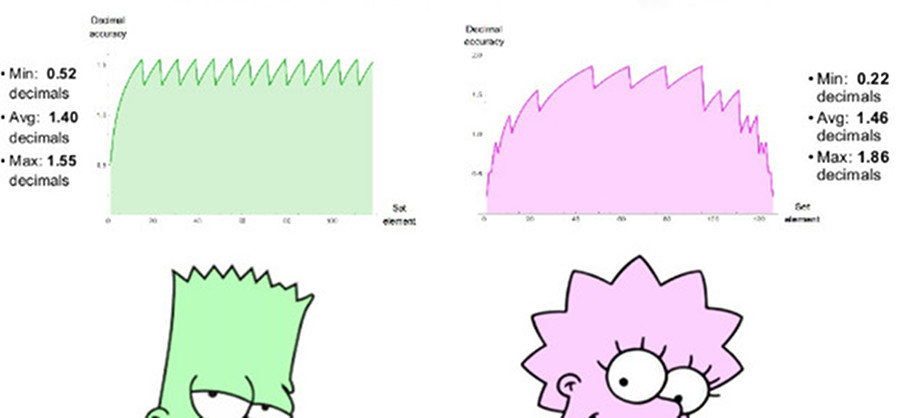
准确性与错误相反。 如果我们有一对数字x和y（非零和一个符号），则它们之间的距离以数量级为单位 $$$\ mid log_ {10}（x / y）\ mid$ 十进制顺序，这与定义最小和最大可表示正数x和y之间的动态范围的方法相同。 在实数系统中，十个数字在1到10之间的理想分布不是数字从1到10的均匀分布，而是指数： $$$1，10 ^ {1/10}，10 ^ {2/10}，...，10 ^ {9/10}，10$ 。 这是工程师长时间用于表达关系的分贝刻度，例如10分贝是十倍的比率。 30db表示系数 $$$10 ^ 3 = 1000$ 。 1db的比率约为1.26，如果您知道精度为1db的值，则精度为小数点后1位。 如果您知道精度为0.1 db的值，则表示精度的2个符号，依此类推。 十进制精度公式为 $$$log_ {10}（1 / \中间log_ {10}（x / y）\中）=-log_ {10}（\中间log_ {10}（x / y）\中）$ ，其中x和y是使用舍入系统计算的有效值（例如，以float和posit格式使用的有效值），或者如果使用严格的使用间隔的系统，则为上限和下限，或者为有效值。

4.2。 定义float和posit比较集

我们可以创建每8位长的浮点数和正数的比例模型。 这种方法的优点是256个值足够小，因此我们可以对其进行完整测试并比较所有内容 $$$256 ^ 2$ 表中出现的加，减，乘和除运算。 精度为1/4的实数具有一个符号位，指数的四位和小数部分的三位，并且遵守IEEE 754的所有规则。最小的正数（已归一化）为1/1024，最大的正数为240，动态范围不对称且相等5.1十进制数，14位组合表示NaN。

可比较的8位正数使用es = 1，正数范围从1/4096到4096，对称动态范围为7.2个十进制数。 没有NaN值。 我们可以绘制两组中正数的十进制精度图，如图2所示。 7.请注意，由正数表示的值的动态范围比浮点数大两个小数位，除浮点数接近于上溢或反溢出的值外，所有值的精度均相同或更高。 两个系统的图形的缩进都是分段线性函数的对数近似。 在浮点数中，精度仅在左侧（在靠近杀伤人员的区域中）下降，在右侧，该功能中断，因为 然后得出NaN的值。 正数在边缘周围具有更对称的递减精度功能。


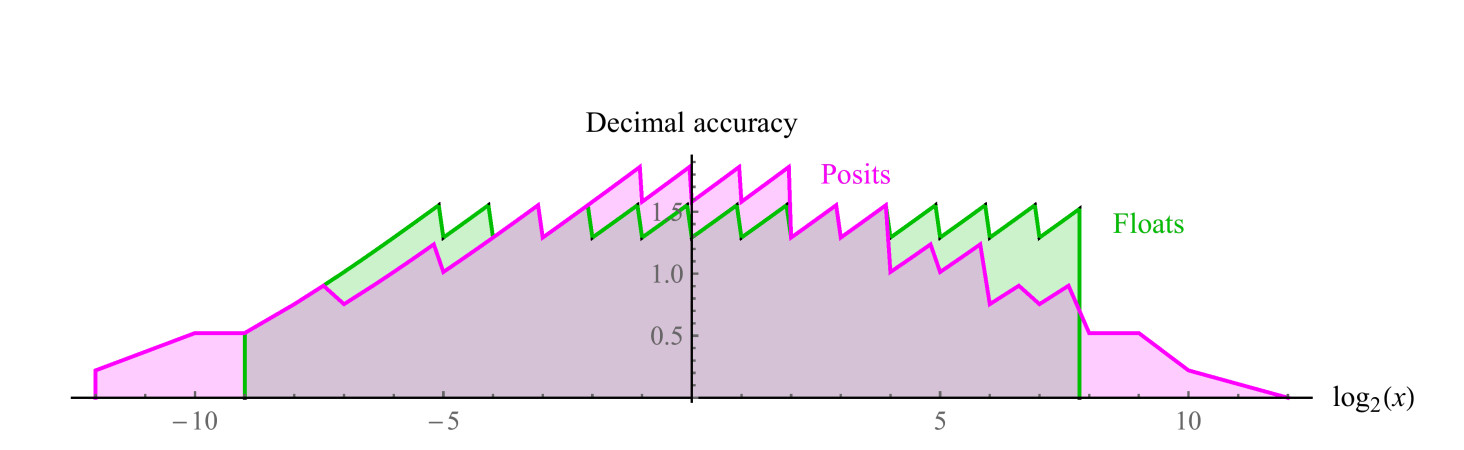
图 7.比较浮点数和正数的十进制精度

4.3。 比较单参数操作

4.3.1。 倒数

对于1 / x函数的每个可能的输入x值，结果都可以恰好与给定集中的另一个值对应，或者可以将其四舍五入，在这种情况下，我们可以使用第4.1节中的公式测量十进制误差，对于浮点数，结果可能导致溢出或NaN。 见图。 8。



图 8.计算反值时，浮点数和正数的定量比较

右图上的曲线显示了计算反值时误差的大小，而浮点数可能会导致NaN。 在许多情况下，正数要优于浮动数，并且在整个范围内都保持这种优势。 计算非规范化浮点数的逆会导致溢出，这会导致无限误差值，并且，当然，NaN自变量给出了NaN的逆。 相对于逆值计算，正数是封闭的。

4.3.2。 平方根

平方根函数不会导致溢出或反溢出。 对于否定参数，对于NaN，结果将为NaN。 回想一下，我们有一个浮点数和正数的“比例模型”，正数的优点随着数据准确性的提高而增加。 对于64位float和posit，posit误差约为float误差的1/30，而不是1/2。

4.3.3。 正方

另一种常见的一元运算是 $$$x ^ 2$ 。 在对浮点数进行平方运算时，经常会出现溢出和反溢出现象。 对于几乎一半的浮点数，平方不会产生有意义的结果，而将正数平方为一个平方始终会产生正数（无符号无穷大的平方是无符号无穷大的平方）。


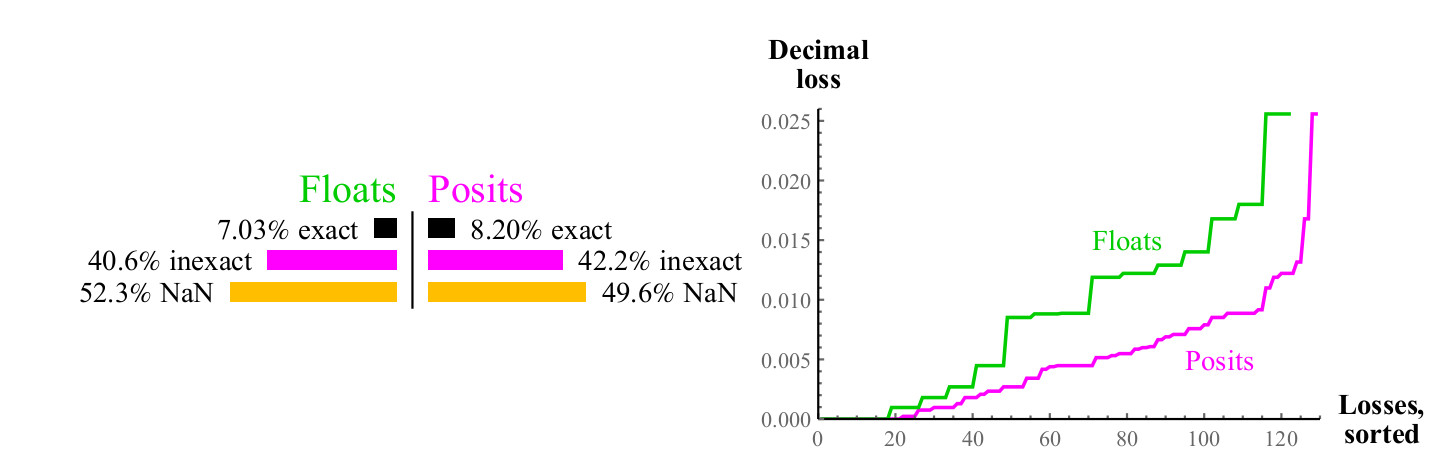
图 9.计算时浮点数和正数的定量比较 $$$\ sqrt x$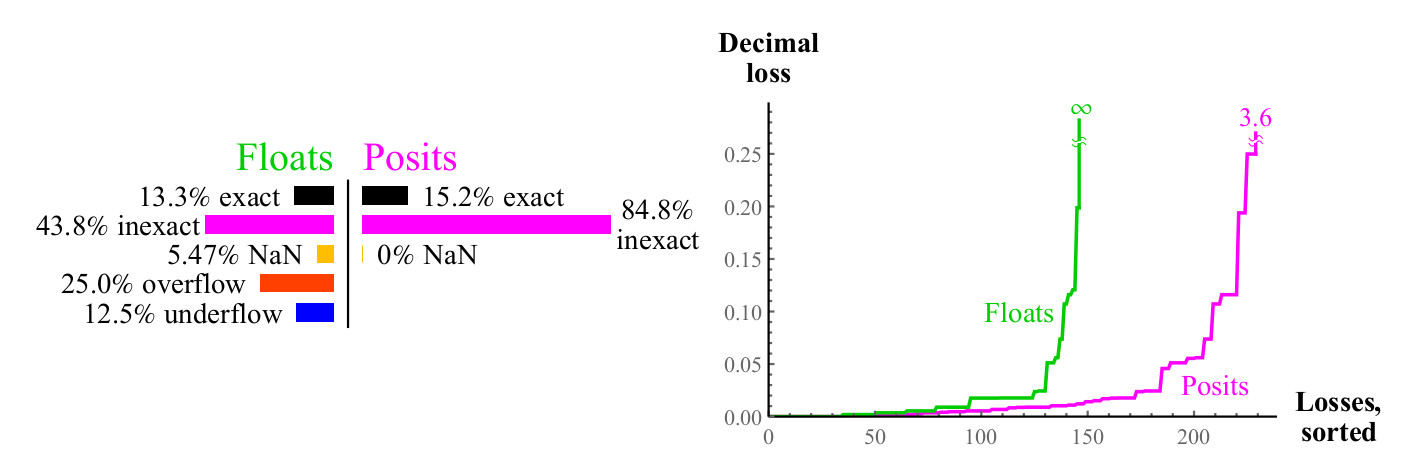


图 10.计算时浮点数和正数的定量比较 $$$x ^ 2$

4.3.4。 以2为底的对数

我们还进行了比较以覆盖以2为底的对数函数，即 $$$log_2（x）$ 可以准确表示，如果不能准确表示，我们会​​损失多少小数位。 在这种情况下，浮点数具有唯一的优势：它们可以用来表示 $$$log_2（0）$ 怎么 $$$-\臭名昭著的$ 和 $$$log_2（\ infty）$ 怎么 $$$\ infty$ ，但这远远超过了一个较大的正数为2的整数幂字典的偏移量。


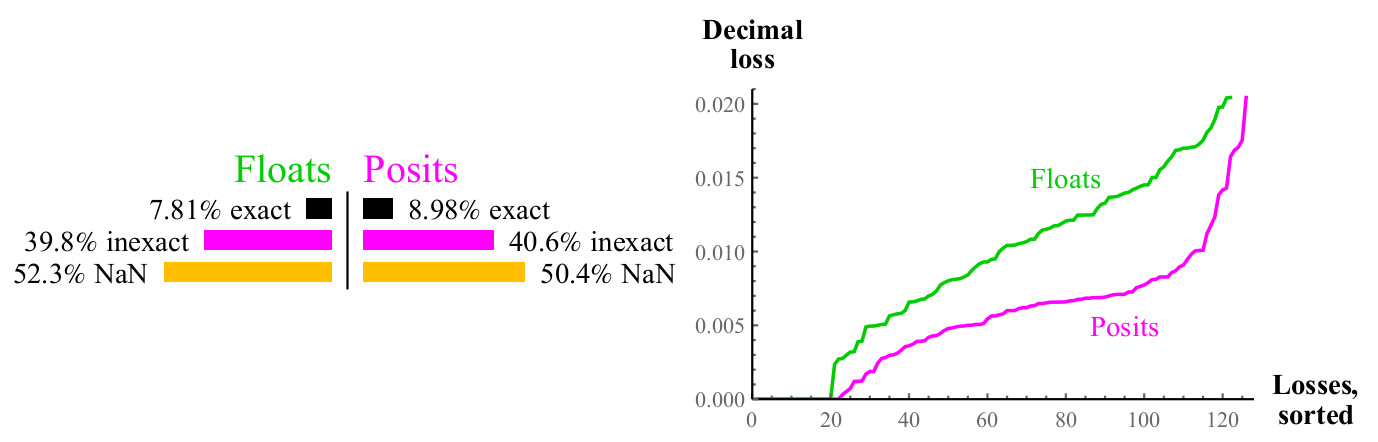
图 11.计算时浮点数和正数的定量比较 $$$log_2（x）$

该图与平方根的图相似，两种情况下约有一半的情况给出了NaN，但正数损失了十进制精度的一半。 如果可以计算 $$$log_2（x）$ ，您只需要将结果乘以比例因子即可 $$$ln（x）$ 或 $$$log_ {10}（x）$ 或任何其他原因的对数。

4.3.5。 参展商 $$$2 ^ x$

同样，如果您可以计算 $$$2 ^ x$ ，您可以轻松地使用比例因子来获得 $$$e ^ x$ 或 $$$10 ^ x$ 等 正数有一个例外， $$$2 ^ x$ 当参数为时等于NaN $$$\ pm \ infty$ 。


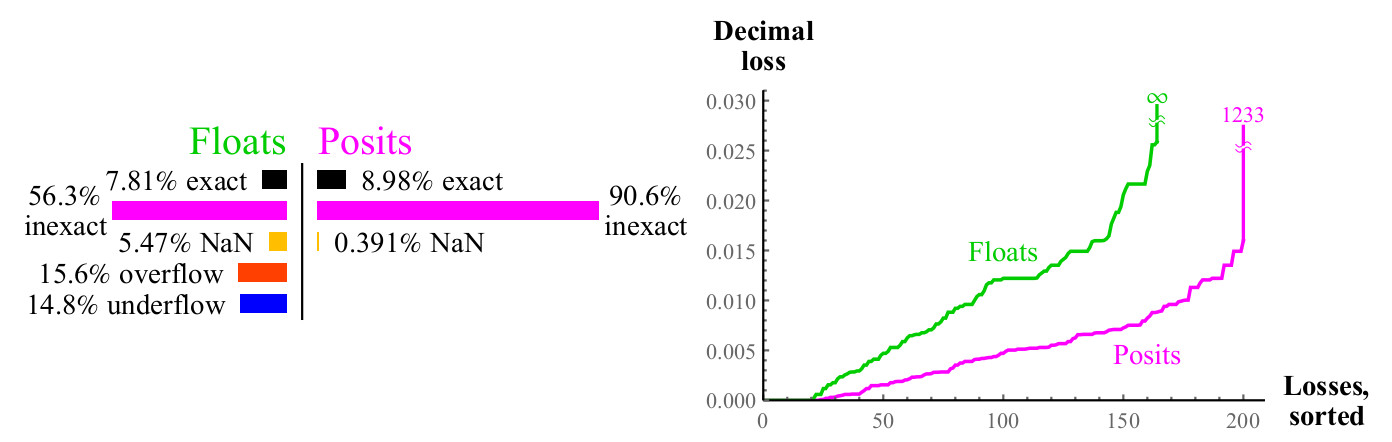
图 12.计算时浮点数和正数的定量比较 $$$2 ^ x$

正数的最大十进制损失可能看起来很大，因为 $$$2 ^ {maxpos}$ 将四舍五入为maxpos。 在此示例中，只有很少的错误与 $$$log_ {10}（24096）\约1233$ 十进制顺序。 确定哪个更好：丢失一千个小数位，还是丢失无数个十进制数？ 如果不能使用这么大的数字，则正数仍然会获胜，因为值较小的错误要好得多。 在所有情况下，当您使用正数时丢失大量小数位时，输入参数远远超出了浮点数甚至无法表示的范围 。 这些图显示了正数在结果有意义的动态范围内如何更稳定，并且在该范围内的精度更高。

对于普通的一元运算 $$$1 / x，\ sqrt x，x ^ 2，log_2（x）$ 和 $$$2 ^ x$ ，posit数比具有相同位数的float数要准确无误，并且在宽动态范围内产生有意义的结果。 现在，我们将注意力转向具有两个参数的四个基本算术运算：加法，减法，乘法和除法。

4.4。 比较两个参数的运算

我们可以使用数字系统的比例模型来研究两个参数的算术运算，例如加法，减法，乘法和除法。 为了可视化65536个结果，我们创建了一个256 * 256的“覆盖图”，该图清楚地显示了准确，不准确，导致溢出，反溢出或NaN的结果比例。

4.4.1。 加减法

由于 $$$x-y = x +（-y）$ 对浮点数和正数都非常有效，无需单独研究减法。 对于加法运算，我们计算出精确值 $$$z = x + y$ ，并将其与每个数字系统中返回的金额进行比较。 可能会出现结果不准确的情况，然后必须将其四舍五入到最接近的有限非零数，溢出或反溢出，否则可能会出现形式的不确定性 $$$\ infty- \ \ infty$ 结果为NaN。 这些案例中的每一个都用彩色标记，我们可以一眼就覆盖整个加法表。 在对结果进行四舍五入的情况下，颜色从黑色（精确值）变为紫色（正值和浮点的精确值）。 图 图13显示了浮点数和unum数的覆盖图。 与一元运算一样，但还有很多要点，我们可以得出有关每个数字系统给出有意义且准确的答案的能力的结论：


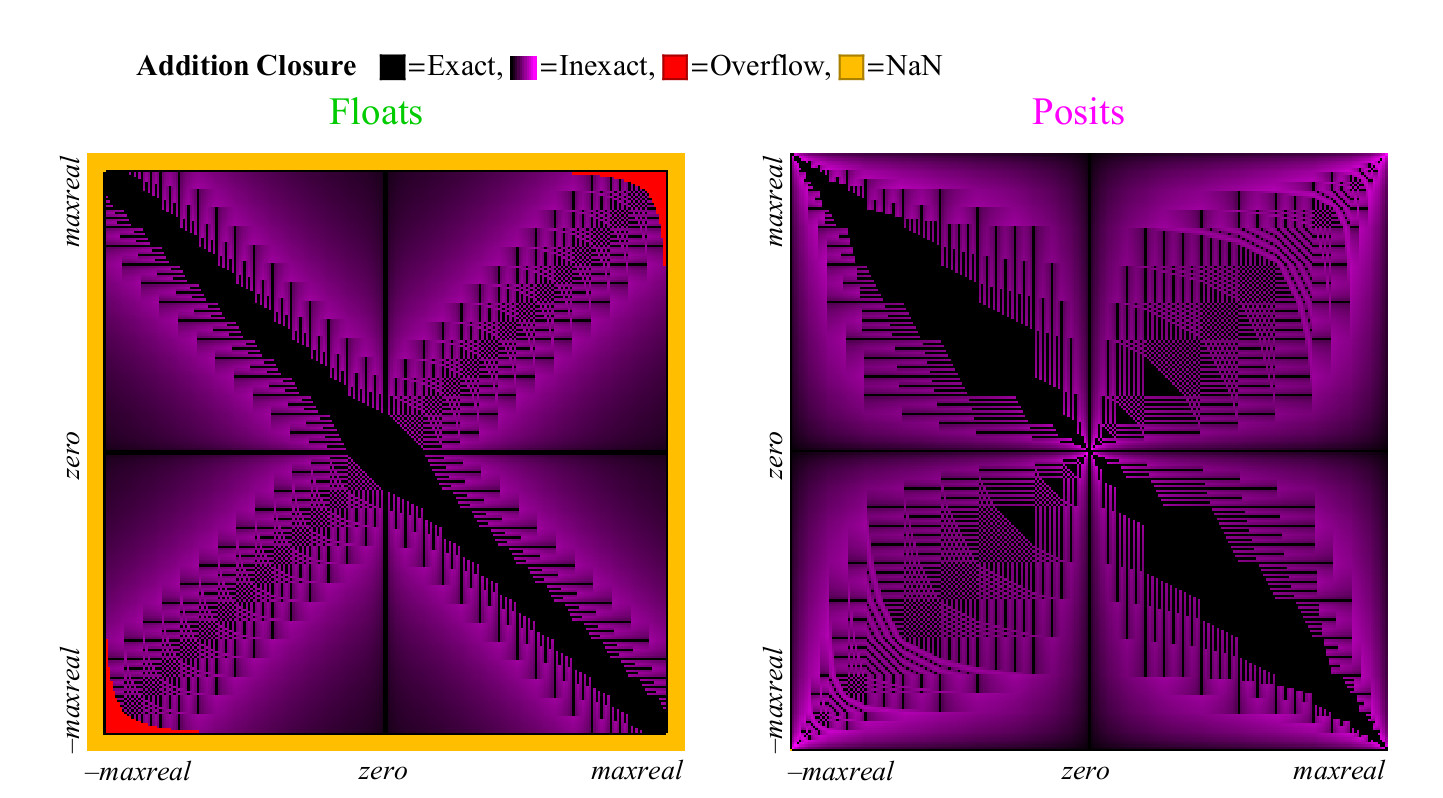
图 13.用于覆盖浮点数和正数的完整覆盖图


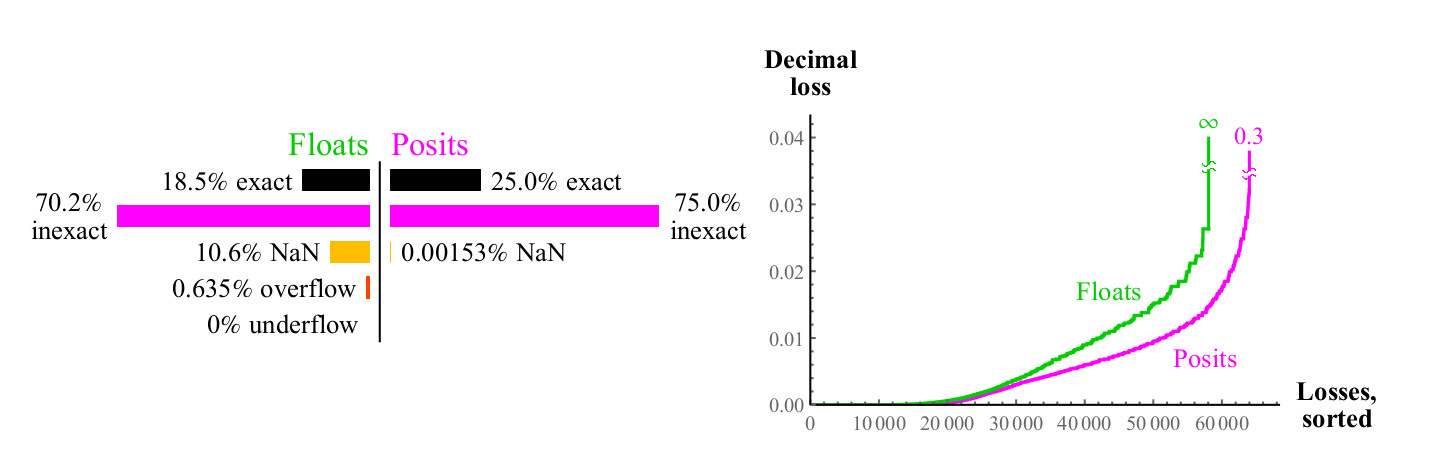
图 14.浮点数和正数相加的定量比较

乍一看，很明显，在加法图中posit有明显更多的点，在这些点上结果是准确的。 覆盖范围图中用于浮动的宽黑色对角线要宽得多，因此精度更高，这是因为它表示非正规化的数字区域，在该区域中，浮动数字以相等的间隔（例如定点数字）间隔开，这样的数字占很大的比例仅在8位数字的情况下为总数的1。

4.4.2。 乘法运算

我们使用类似的方法比较浮点数和正数的乘积。 与加法不同，乘法可以引起浮点数的反溢出。 “逐步防溢出”，您可以在图15的中心看到的区域。 在左边 （ 表示非正规化数字。大约为transl。 ）如果没有该区域，则蓝色的防溢出区域将具有菱形形状。 正数的乘法图的色彩较少，更好。 仅两个像素被高亮显示为NaN，靠近轴的零标记所在的位置（ 像素在垂直中心居左，水平居中中心在底部。大约是Transl。 ）有乘法结果 $$$\ pm \ infty \ cdot 0 = NaN$ 。 浮点数表示产品准确但价格低廉的情况更多。 如图15所示，几乎所有浮子产品的1/4都会导致上溢或反溢出，并且随着浮子精度的提高，该比例不会降低。


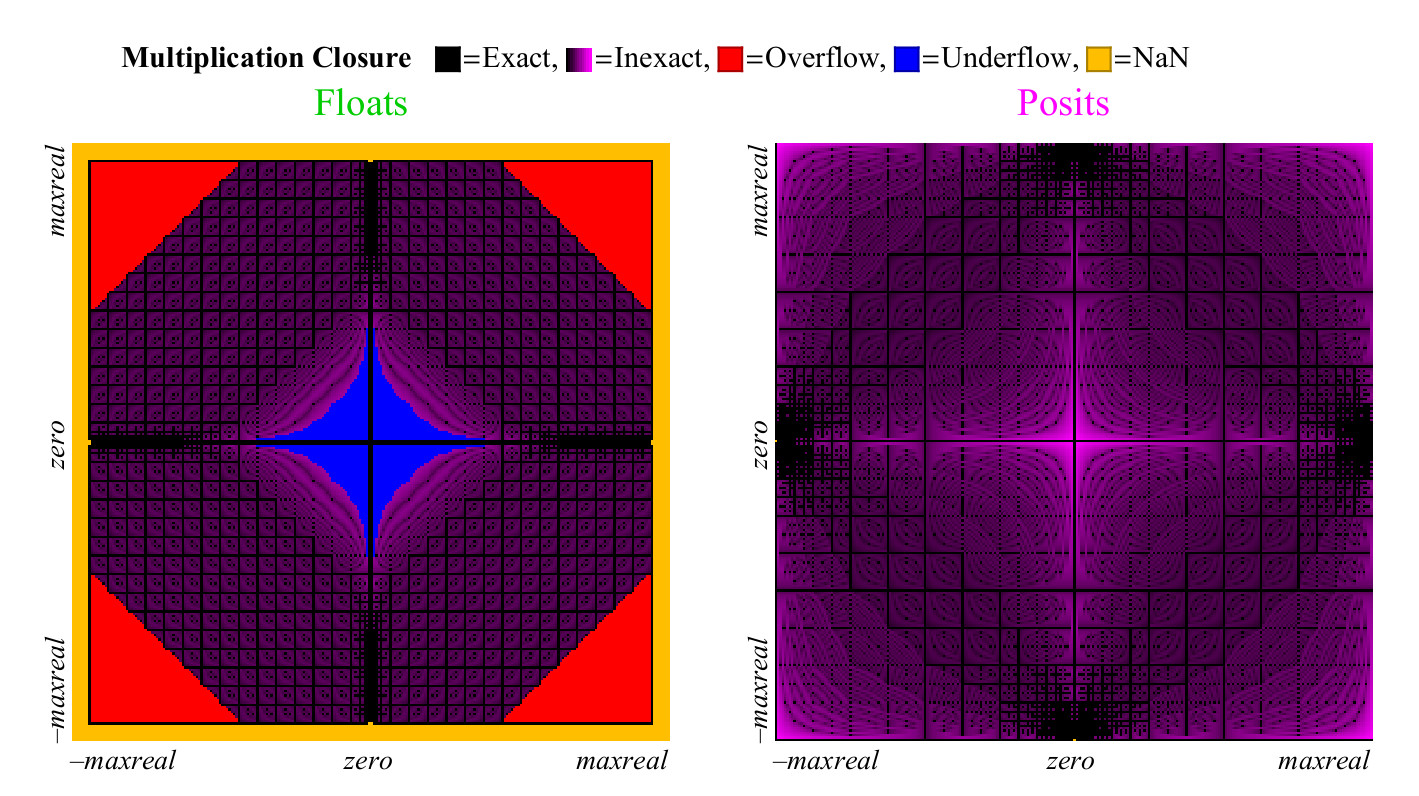
图15.乘以浮点数和正数的完整覆盖图

对于正数四舍五入的最坏情况是 $$$maxpos \乘以maxpos$ 再次舍入到maxpos。 在这种情况下（非常罕见），错误为3.6个十进制顺序。 如图所示。 16，正数明显优于浮点数，最大程度地减少了乘法误差。


图 16.浮点数和正数相乘的定量比较

除法运算的覆盖图类似于乘法图，但是为了节省空间而对区域进行了交换，此处未显示。 除法的量化指标几乎与乘法相同。

4.5。 比较浮点数和正数以评估表达式

4.5.1。 测试“ 32位精度预算”

测试通常是在最小运行时间的基础上进行的，并且通常无法完整地说明结果的准确性。 另一种类型的测试是我们确定错误的预算，即每个变量的位数，然后尝试获得最大的十进制精度。 这是一个表达式的示例，可用于比较每个数字的预算为32位的数字系统：

$$

$$X = \左（\ dfrac {27 / 10-e} {\ pi-（\ sqrt 2+ \ sqrt 3）} \ right）^ {67/16} = 302.8827196 \ dotsb$$

规则是我们从数字的最佳表示开始 $$$\ pi$ 和 $$$e$ ，可能的每个数字系统以及所有指示的整数的表示形式，并且在表达式中执行9次运算后，我们看到多少个十进制数字与X的真实值匹配。 我们将用橙色突出显示错误的数字。

尽管32位IEEE浮点数具有十进制精度，范围从7.3到7.6十进制数，但是X的计算中舍入误差的累积给出了302. 912的答案，它只有三个有效数字。 这是用户感到到处都需要使用64位浮点数的原因之一，因为即使简单的表达式也可能会失去准确性，以至于结果可能毫无用处。

32位正数具有可变的十进制精度，对于绝对值约为1的数字，其十进制精度范围为8.2至8.5。在计算X时，它们给出的答案是302.882 31，该位数是有效位数的两倍。 同样不要忘记32位正数的动态范围超过144个小数位，而32位浮点数的动态范围更小，只有83位。 因此，无法通过缩小动态范围来实现结果的额外准确性。

4.5.2。 四重检验：戈德堡的细三角问题

有一个经典的“细三角形”问题[1]：当边b和c的两个只有3个最小有效数字单位（最后一个单位，ULP）长于长整数的一半时，找到边为a ， b ， c的三角形的面积侧面（图17）。


图 17.戈德堡的细三角问题

区域A的经典公式使用中间变量s：

$$

$$s = \ frac {a + b + c} 2; A = \ sqrt {s（s-a）（s-b）（s-c）}$$

此公式中的危险是s非常接近a的值，并且计算 $$$（s-a）$ 极大地增加了舍入误差。 让我们尝试使用128位（四倍精度）的IEEE浮点数 $$$a = 7，b = c = 7/2 + 3 \乘以2 ^ {-111}$ 。 （如果以光年为度量单位，则短边的长度将比长边的一半长，仅为质子直径的1/200。但这使三角形成为顶部门口高度的三角形。）我们还使用128位正数计算A的值（ es = 7）。 结果如下：

$$$$ display $$ \ begin {matrix} \ textrm {True value：}＆3.14784204874900425235885265494550774498 \ dots \ times 10 ^ {-16} \\ \ textrm {128-bit IEEE float：}＆3. \ color {orange} { 63481490842332134725920516158057682788} \点\倍10 ^ {-16} \\ \ textrm {128位位置：}＆3.147842048749004252358852654945507744 \颜色{orange} {39} \点\倍10 ^ {-16} \结尾{matrix} $$显示$$

正数最多具有1.8个十进制数字，其精度大于在宽动态范围内的四倍精度浮点型：从 $$$2 \乘以10 ^ {-270}$ 之前 $$$5 \乘以10 ^ {-269}$ 。 这足以防止在这种特定情况下增加错误的灾难性后果。 有趣的是，即使最后我们将其转换为16位正数，正数格式的答案也将比浮点格式的答案更准确。

4.5.3。 二次方程的解

有一个经典技巧可以避免在计算根时舍入错误 $$$r_1$ ， $$$r_2$ 方程式 $$$ax ^ 2 + bx + c = 0$ 使用通常的公式 $$$r_1，r_2 =（-b \ pm \ sqrt {b ^ 2-4ac}）/（2a）$ 当b远大于a和c时 ，这导致左侧数字消失，因为 $$$\ sqrt {b ^ 2-4ac}$ 非常接近b 。 但是，与其强迫程序员记住神秘的技巧，不如通过使用教程中的一个简单公式来使计算安全，这可能更好。 放 $$$a = 3，b = 100，c = 2$ 并以32位float和posit格式比较结果。

表5.二次方程的解


数值不稳定的根- $$$r_1$ ，但请注意，32位正数给出6个正确的数字，而不是浮点数的4个数字。

4.6。 经典LINPACK测试的浮子和正位置系统比较

长期以来，评估超级计算机的主要方法是求解 $$$n \倍n$ 线性方程组 $$$\ mathbf Ax = b$ 。 即，测试用从0到1的伪随机数填充矩阵A ，并用行A 的总和填充向量b 。 这意味着解x是由单位组成的向量。 测试计算扣除率 $$$\ | \ mathbf Ax-b \ |$ 验证正确性，尽管答案中没有固定的数字位数。 测试通常会损失几位数的精度，并且通常使用64位浮点数（不一定是IEEE）。 最初，测试提供了n = 100，但是对于最快的超级计算机来说，这个大小太小了，因此n增加到300，然后增加到1000，最后（第一作者），该测试变得可扩展并给出了每秒的操作数，基于测试执行的事实 $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ 乘法和加法运算。

通过比较正负浮动，我们注意到了该测试的一个小缺点：由于行中总和的舍入误差，通常情况下的答案不是单位序列。 如果我们发现A中的出现如何贡献1位（超出了可能的精度范围）并将此位设置为0，则可以消除这种错误。这将使我们充满信心，A行的总和可表示而不进行舍入，并且答案为x实际上是一个由单位组成的向量。 对于任务的原始版本（大小为100x100），64位IEEE浮点型给出了以下答案：

0.9999999999999 633626401873698341660201549530029296875
1.00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1.0000000000000 22648549702353193424642086029052734375

100个数字中没有一个是正确的； 它们接近1但从不等于1。有了正数，我们可以做一件很棒的事情。 使用32位正数和相同的算法，我们计算残差 $$$r = \ mathbf轴-b$ 使用合并操作是标量产品。 然后决定 $$$\ mathbf轴'= r$ （使用已处理的 $$$\ mathbf A$ ）和使用 $$$x'$ 进行更正： $$$x \ leftarrow x-x'$ 。 结果是LINPACK测试前所未有的准确答案： $$$\ {1，1，...，1 \}$ 。LINPACK规则是否可以禁止使用新的32位数字类型，使用该数字可以实现零错误的完美结果，还是会继续坚持使用不允许的64位浮点数？该决定将由负责此测试的人员做出。对于那些需要解决线性方程组来解决实际问题而不是比较超级计算机的速度的人，posit提供了惊人的优势。

5.结论

Posit在自己的游戏中击败了花车：使用它，您可以执行计算并减少取整误差。正数具有更高的准确性，更大的动态范围和更大的覆盖范围。与相同位深度的浮点数相比，或与较低位深度的相同结果相比，它们可用于获得更好的结果。由于系统带宽有限，因此使用较小的操作数意味着更快的速度和更低的功耗。
由于它们作为浮点而不是间隔系统工作，因此可以将它们视为浮点的直接替代，如此处所示。如果使用float的算法通过了测试，并且时间和稳定性都“足够好”，那么使用posit可以更好地工作。 posit中可用的融合操作提供了一个强大的工具来防止舍入误差的累积，并且在某些情况下，允许您在需要高性能的应用程序中安全地使用32位posit数代替64位浮点数。通常，这将使应用程序性能提高2-4倍，并降低功耗，节省能源并降低数据存储成本。硬件支持的假设将为我们提供相当于摩尔定律的一两个步骤，无需减小晶体管的尺寸或增加成本。与float不同，posit系统提供了不同系统上结果的逐位可重复性，消除了IEEE 754标准的主要缺点，posit数字比float更简单，更优雅，并减少了支持它们的设备数量。尽管浮点数现在无处不在，但正数可能很快会使它们过时。

参考文献：

1. 大卫·戈德伯格。每位计算机科学家都应该了解浮点运算。
ACM计算调查（CSUR），23（1）：5–48，1991。DOI：doi：10.1145 / 103162.103163。
2. John L Gustafson。错误的终结：Unum Computing，第24卷。CRC出版社，2015年
。3. John L Gustafson。超越浮点：下一代计算机算法。斯坦福大学研讨会：https：//www.youtube.com/watch？v = aP0Y1uAA- 2Y，2016年。完整转录本
可在http://www.johngustafson.net/pdfs/DebateTranscription.pdf上找到。
4.约翰·古斯塔夫森（John L Gustafson）。一种使用实数进行计算的根本方法。超级计算
前沿与创新，3（2）：38–53，2016. doi：http ://dx.doi.org/10.14529/jsfi160203。
5.约翰·古斯塔夫森（John L Gustafson）。大辩论@ ARITH23。https://www.youtube.com/watch?v=
KEAKYDyUua4，2016年。完整转录本可在http://www.johngustafson.net/pdfs/
DebateTranscription.pdf上找到。
6. Ulrich W Kulisch和Willard L Miranker。一种新的科学计算方法，第7卷。Elsevier，2014年。7
.更多站点。IEEE浮点算术标准。IEEE计算机协会，2008年
。DOI：10.1109 / IEEESTD.2008.4610935。
8.米萨尔（Isaac Yonemoto）。https://github.com/interplanetary-robot/SigmoidNumbers