碰巧科学发展不平衡,因此,在我们今天的生活中,可以说有成就的空间。 这当然是一项科学的壮举,但是从这一点来看同样重要。 现在,读者可以借此机会了解壮举的位置,付款的官方价格(这在自称为文明国家的惯例中),甚至可以自己试试运气。 好吧,与此同时,至少你们中的某些人会感到在非常普通的事物中发现珍珠的魅力。
此外,在几个系列中,将跟随一个故事,讲述任何高中毕业生(甚至许多学童)都可以使用的东西。 因为它们经常是显而易见的,所以将没有证据,如果在此处显示,它们不仅会扩大体积,还会吓倒许多读者。
第一个系列
首先有星星。 有一个与他们一起玩耍的过程,注视着并感受着,折腾并观察闪闪发光的秋天。 星星是图案。 数字是沙盒。 数字翻开了新的面,彼此之间的缝隙中又出现了一颗星星。 她的容光焕发,最重要的是没有燃烧,但被抚摸,捡起,然后向他们挥手致意,留下了星光灿烂的痕迹。 但是后来星星变得熟悉了,剩下的工作就是对它们进行分类了。 然后一个主意出现了。
这个想法很简单-您可以从中赚钱。 是的,它确实具有动机。 但是它并没有一起成长。 这很有趣,有规则的恒星以一种新的方式发光,有快乐,有进步。 直到最后才出现了一片森林,一片不断发光的森林。 而且我很虚弱,我无法对这种针叶林进行分类以寻找真正的光线,因为那里有数百万棵树,而且我一个人。 因此,我建议您看看星星,如果它们很有趣,那么您可以赚到40万美元,但事实是只有一个“但是”-在森林中,您需要能够选择正确的道路。
关于通往星星的方法
什么是数字? 一方面,它是我们阴郁的头脑的产物,自然界中找不到。 但是另一方面,这样的抽象使我们可以对许多我们观察到的具有相同性质的过程进行建模。 仅模型不等于观察到的现象。 因此,我们再次要适应对我们描述自然的方式的适度能力。 这样好吗 在准确性方面,描述不是很好。 不是因为某人可能没有足够的小数位数,而是因为一个不正确的建模现象会在发现模型缺乏现实中存在的一个或另一个特定功能,甚至有时听起来有些烦人时使我们感到惊讶不专心的博物学家在头上。
鉴于上述情况,让我们尝试询问任何建模基础的完整性-理解数字概念的完整性。 似乎只有从幼儿时期就积累下来的一些知识,对吧,还有什么呢? 但是就在那儿我们可以找到深渊。 是的,那是无底的,到处都是星星。
自然界中没有数字。 但是在自然界中您可以看到这种关系。 云比另一个云更大(更长/更宽/更厚/ like_you_ else_will_be_coming),这意味着存在一个相关的地方。 但是比率也没有数字。 只有两朵云,一朵多一点,另一朵少一点,并且有它们的比率。 虽然可以,但是这个比率也是人为发明的。 因此,可能会问-它的用途是什么? 这样做的好处是-关联的概念比数字的概念领先一步。 起初有一个比率,然后才出现一个数字。 更准确地说-小数。 因此,了解关系之后,我们将了解数字。
如何获得小数? 非常简单-从需要模型关联。 起初有台阶和土地的比例,一个主人的绵羊与另一个主人的绵羊,一个西瓜的重量与另一个西瓜的重量。 在所有这些情况下,都需要以某种方式表达差异。 但是,差异并未严格按照步数或相邻西瓜的大小进行划分。 最初,他们学会了通过将它们分成较小的度量单位来表达差异(将肘部添加到步骤中,并将手指添加到肘部中)。 但是科学并没有停滞不前,并要求更高的准确性。 结果,每个人都同意均匀性,而忘记了手指,肘部,台阶和其他带有英镑的磅数。 均匀性用数字表示。
如果两个细分中的一个细分不适合另一个整数,该如何关联两个细分? 您可以用手指进行测量,但是将较小的段作为测量单位并分成相同的部分会更准确。 使用这些部分,您可以测量较大分段中未被整个较小分段测量的部分。 但是随后出现了较大部分的新部分,该部分不再可用所选部分进行测量。 我们应用递归,然后将已经损坏的部分再次分解为更小的组件。 我们对其进行了以前无法衡量的评估。 再一次,我们得到了不可估量的余数。 再次分开零件,再次测量。 再次,我们得到其余的。 但是你会觉得无聊!
结果,人们想到了舍入的概念,并停止了重新划分度量单位。 也就是说,人们对准确性进行了评分(他们说这是足够的)。 但是自然不会原谅建模的不准确性。
今天如何模拟比率? 使用分数数字的分类对它们进行建模。 分类是这样-有整数,有小数。 整体仍然不稳定,但小数分为有限分数和无限分数。 就目前而言,我们也忘记了最后一个。 无限分为理性和非理性。 我们通常会忘记第一部分。 非理性分为代数和先验。 一切,没有更多的分裂。 但是为了清楚起见,我们以图片的形式进行分类:
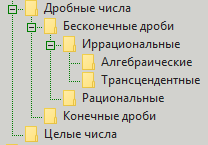
为什么这个分类不好? 她还不错。 正如小熊维尼(Winnie Pooh)所说,她很好,但还是有点some脚……就是说,很显然,由于表达了价值的准确性,她由于无穷无常而没事。 但是,硬币还有另一面。 这一方面(在这种情况下)称为“可分割性”。 我们不能精确地将两个数字分开(一个数字一个数字),因为我们反对无穷大。 但是,另一方面,我们对诸如数字的世界这样的现象很感兴趣,例如简单性和在出现时消除无穷大的除数。 质数构成整数序列的基础。 这些重要的数字(例如,包括在远程支付服务时的舒适度)在很大程度上取决于划分操作。 除法常常给我们分数。 分数给我们分数。 好吧,对于分数,有人给了我们先前给出的有限,无限,有理,无理,代数和先验的分类。 但是,这种分类是否使我们有机会找到有关数字问题的答案? 例如,大约相同的简单的? 还是分数? 它似乎给了我们,但没有我们想要的那么多。
取质数。 如今,基本上已经在搜索最大素数。 即,他们获取候选编号,然后检查其是否简单。 候选人简单地获得数字-如果您知道检查某一类数字的简单性的方法,那么以下是他们连续愚蠢地经过的类代表的形式的候选人列表,检查每个数字,当然从小数值开始。 到目前为止,它们的数量已经达到了大约两千个,达到八千万。 这几乎是2千5百万个小数位。 原则上,它看起来令人印象深刻。 但是,是什么使我们无法回忆起“更高,更远,更快”的口号?
从根本上说,我们缺乏了解阻碍了我们的发展。 是的,我们称为“数字”的现象模型是不完整的。 是的,该模型的称为“除法”的部分在最大程度上是不完整的。 因此,计算机内存中的八千万个单元是人类的极限。 为什么要单位? 因为它看起来像最大的质数。 这些是一个单位,但采用二进制表示法。 对于他们来说,有一个Luc-Lemer检验,它向我们展示了一个简单的数字或一个复合词。 这项测试需要一个处理器内核多年的工作来检查八千万个二进制单元的候选数量。 只有80兆字节或10兆字节,人类不再能够进一步前进。 什么是十兆字节? 这是一分钱,这是一件小事,对于现代计算机而言几乎没有。 但是测试已经进行了多年。 因此,您必须在志愿者安装了适当程序的数百万台计算机上运行该程序,结果在一个特定的秒数内检查一个候选编号(如果有很多志愿者,则要检查此编号)。 但是问题在于候选号码很多,因此要花下几个月才能找到下一个素数。 通过这样的讨论,可以预期,仅上亿个二进制单位的移动将花费十年。
是否可以加快流程? 可以的 但是需要更多的理解。 例如-如何减少测试每个数字的时间? 到目前为止,这种减少是通过按摩铁来实现的。 或第二种选择-您可以提供更快速的简单性测试。 但是,在大约100年的时间里,几乎没有什么变化。 但是,如果您能解决问题,那么也许它将与我们合作。 只需要从最基本的方面理解。
附近的星星
考虑到这种关系,每个人都可以为科学做出很大贡献。 只是好奇就足够了。 例如,一个人可能会问,为什么小数的分类就是这样? 并在思想实验中找到答案,以测量相同部分的比率。 首先,各段之间的关联为1到2。这个比率是可以理解的,它为我们提供了数字2,该数字表示较大的段超过较小的段的次数。 现在,我们拉长一小段。 会发生什么? 该比率将不再是完整的。 从延长中获得的多余部分使我们无法获得问题的简单答案。 但是我们可以将其用作标尺。 如果它适合较大整数部分中一半的整数倍,则可以通过该整数表示比率。 因此我们得到比率:
其中N是将多余的长度从较小的长度拉伸为较大的长度的一半所需的次数。 这样我们得到一个有理数。 它总是由整数比给出。 如果现在将较小的段加长一点,那么就会出现这样的情况:无论将较小段乘以某个整数多少,我们都无法获得与较大段的一定长度的精确匹配。 因此,我们得到了一个非理性数字来表征新比率。 注意,段边界的微观移动导致识别长度比的无穷过程。 谦虚的研究人员迈出了一步,而数论则发生了巨大变化-分类中需要一个新元素。 一步-从微观尺寸到无限。 从一类数字到一个全新的数字,与上一个数字根本不兼容。 那不是星星吗?
但实际上,我们只是稍微改变了一个细分市场。 那么,根本上新的类别从何而来? 总的来说,分类对于其准确匹配现实的能力很重要。 但是非理性数字会带来什么样的准确性呢? 它们使您可以为任何比率建模,而不仅仅是整数比率,因此分离此类非常有意义。 但这还不是全部准确性,因为我想了解所有这些无限性,它们的出现方式,含义以及根本存在的原因。 的确,对于无限性,一切都不容易,但是因为现在我们将处理有限的关系。 他们似乎一切都很简单,取N,除以M,然后得到一个分数。 如果数字短,例如2.5或3.25,那将是非常好的。 但是,世界上经常出现4.12(3456)形式的关系,也就是与无穷大,但是这些是“周期内”的无穷大。 只需注意重复的数字,您就可以非常轻松,紧凑地记录无数个字符中的数字。 这就是我们著名的应对无限性的方式。 还有一个小星号。 但这只是一个粗略的浏览。
现在,让我们打开好奇心并提出问题。 为什么有些分数是有限的而另一些是无限的? 为什么有些类型的无限长,而另一些带有周期? 为什么在数字4.12(3456)的句号之前看到数字1和2? 为什么存在一个前期? 为什么在此期间我们看到数字3和4? 在这个例子中,为什么周期长度等于四? 为什么在周期前的数字等于2? 而且,我们仅对一个小数进行了表面研究。 对于其他数字,这些问题将更加有趣。
让我们尝试回答。 为什么分数是有限的? 非常简单-实际上,这是“视觉错觉”。 更准确地说-我们使用了一个技巧。 例如,要获得数字2.5,可以将5除以2。为此,我们所有人都在学校教过“角”除法。 但是,让我们仔细看看这种方法。 然后我们发现骗子的行为如下-将股息乘以包含除数或其因子的常数。 然后,它将从常数到除数的因数精确地减小。 看起来像这样:
这就是所有奇迹-分频器的减法减少为常数的减法
等于
,结果剩下五分之一,将其写入小数点分隔符之后。 这个数字是
从未共享
,它乘以
从金额
。 但我们看不到这一点,这要归功于我们从学校训练来的“光学幻觉”,以便在每个师的师生作业中独立创建。 好吧,那不是星星吗? 从小学时代起,当我们看到一种新的,不是很平常的东西的光时,人们只需将树叶推向柔弱的表象,这不是在学校里教过的,而是徒劳的。
现在让我们在更高的层次上解释“光学错觉”。 我们仅将除法结果转换为便于存储和感知的格式。 数字本身并不取决于格式。 并且其中的字符数也是。 我们已经看到了将括号放在一个句点周围的可能性,从而减小了句点和两个括号长度的无限性。 这也是一种数据格式,但用于周期分数。 有限分数的格式通过从十进制数系统的底数减少因子来隐藏无穷大。 例如,如果我们采用三进制数系统,则将5除以2将看起来像这样:
也就是说,我们得到了周期分数形式的无穷大,因为现在我们使用了另一个常量,该常量不包含可以用数字2减少的因子。但是在十六进制系统中,结果将再次变为最终的2.3。 但是数字本身仍然处于阴影中,可能最好的记录是5/2,其他所有事情都是选择该数字的显示格式。
现在关于无限分数。 周期数是通过对整数除以得到的,无理数(具有无限的周期长度)是通过从整数计算一定程度的根来获得的。 也就是说,人们从整数的抽象中得出两类除法-具有不同的因子和相同的因子。 第一个选项允许您将任何整数除以任何其他整数,但有时会给出分数结果。 第二个选项允许您仅将数字除以与除法结果完全相等的数字(包括大数根的倍数)。 通常,我们具有相同的划分,但对结果没有限制,并且不受限制。 这种限制导致我们有两种选择:要么将除数除以除数的一个因子(然后就可以得到一个等于除数的整数),要么将不可约数除以一定的数。 那么什么是“特定数字”呢? 如果它是整数,那么结果是我们得到的分数(除数和除数不可约)不等于整数。 因此,由于整数不适合,您需要查找等于结果的分数。 有限分数也消失了,因为它们实际上代表了多种形式
当自身相乘时,会给我们形式的新分数
,这再次为我们提供了有限的或周期性的分数,而不是整数。 因此,必须选择一个分数,该分数将减小它们的平方与无穷大的N和M的整数之比。 为什么要使用无穷整数比例
可以做成整体,但不是最终? 因为数字越多,离散度对结果的影响越小。 任何选择的一个后跟的整数必然与它相差一个。 并且此单元不允许您精确设置所需的结果,因为例如在1/1000和2/1000之间有无限多个数字,例如11/10000或145/100000等。 因此,增加数目的长度,可以无限地以任何精度获得任何结果。 然后将其自身相乘得到一个整数。
同时,如此小数的周期实际上变得无限,正如我们稍后将看到的。无穷数是无理数的性质,无理数已由完全有理数传递给无理数。这里是这样的星光,平滑地变成了无限的黑暗。? ? . , , . . ? , ( ) . . , - . — , , «» . . . . . . , , . — ( ) (, , , ). , , , . () . , , , , . «», , , , , , — . . «» , ? , — , , .
现在就这些了。在下一个系列中,让我们讨论有理恒星。