如何正确为多项式着色

多项式不仅是抽象问题的练习。 它们非常适合在意想不到的地方检测结构。

2015年，何鸿a曾是一名诗人，后来成为数学家，他帮助解决了大约50年前提出的问题。 它与复杂的数学对象，“ 拟阵 ”和图形（点和线段的组合）相关联。 而且它还与多项式有关-从数学课程中我们所熟悉的表达式，包括各种程度的变量之和。

在学校的某个时候，您可能经历了多项式中括号的打开。 例如，您可能还记得x ² + 2xy + y ² =（x + y） ² 。 一个方便的代数技巧，但是在哪里可以派上用场呢？ 事实证明，多项式完全有助于揭示隐藏的结构-Ho积极地在证明中运用了这一事实。 这是一个简单的谜语，说明了这一点。

假设我们需要在一个正方形的桌子上坐两队球员。 为防止欺诈，您需要确保球员不要坐在团队中其他球员旁边。 有几种座位方法？

让我们从红色和蓝色团队的座位开始。 假设红色玩家位于图表的顶部：



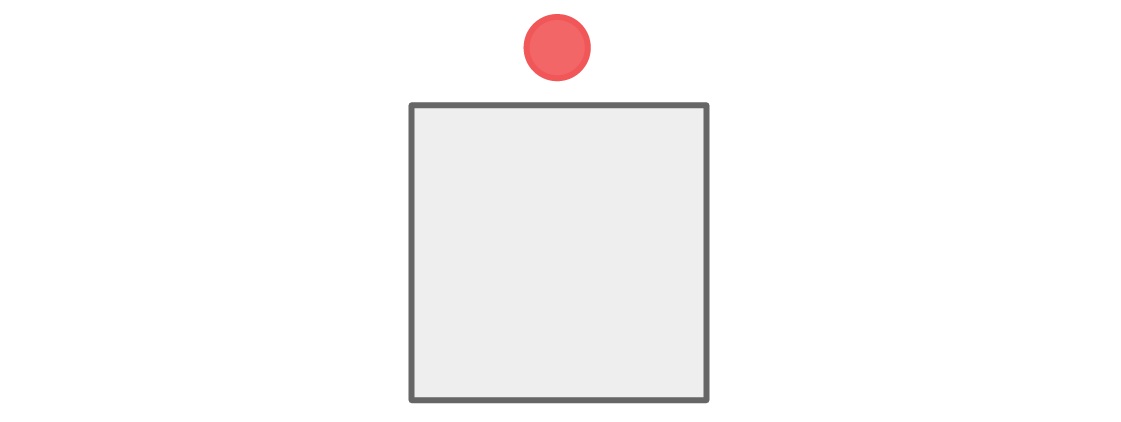
在最高位置附近有两个位置-右侧和左侧-为了满足规则，这些位置必须由蓝色玩家占据。



下面的空间与两个蓝色的空间相邻，因此红色的玩家必须坐在那里。



没有一个球员坐在团队成员旁边，我们的条件得到满足。

我们也可以从顶部的蓝色播放器开始。 类似的考虑导致以下安排：



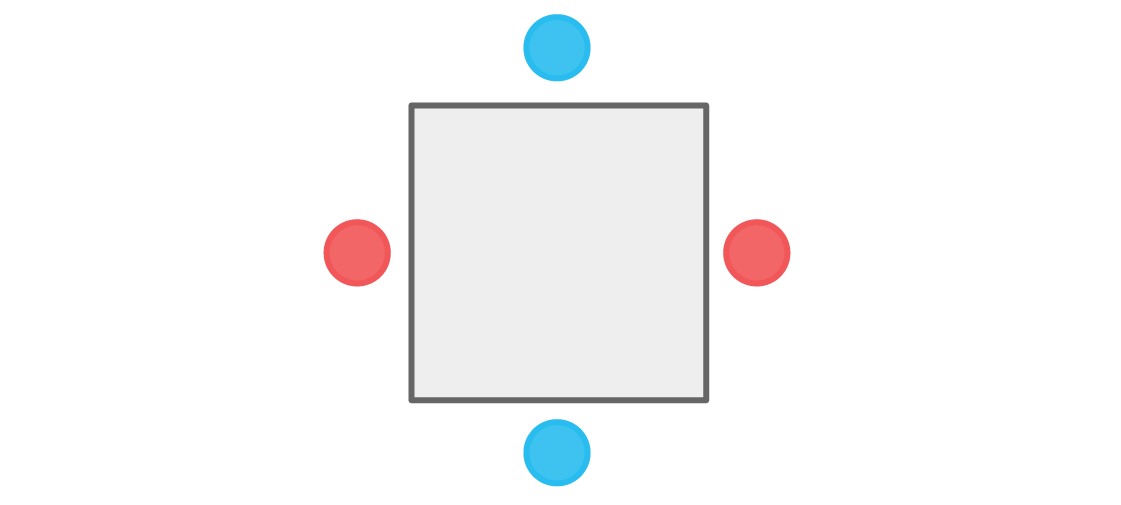
同样，没有球员坐在他的团队的其他成员旁边。 我们的条件得到满足，这样的座位安排是可以接受的。 实际上，恰好有两个这样的座位安排。 一旦我们选择了最上面的颜色，其余的就全部定义好了。

有一种方法可以找出只有两种可能的座位安排而无需绘制所有这些图表。 让我们从顶部开始：我们有两个选项，红色和蓝色。 选择此选项后，左右座椅仍然有一个选项（不同的颜色）。 对于下排座椅，只剩下一个选择-我们开始使用的颜色。 使用“计算的基本原理”，我们知道机会总数是每个选项的机会数目相乘的结果。 正如我们从图中确定的那样，这使我们获得2×1×1×1 = 2的幼苗。

现在，用第三种颜色添加第三个命令。 想象我们有红色，蓝色和黄色的球员。 如果相邻的地方必须使用不同的颜色，可以安排多少个座位？ 对于所有可能性的图像，您将不得不绘制整个图表，因此让我们尝试进行计算。

对于最高点，我们现在可以选择三种颜色。 选择之后，我们可以为左右两个位置选择剩余的两种颜色。

广场下面会是什么？ 倾向于声明最后一个座位只有一个选择，因为它在左右座位旁边。 但是，您觉得这种逻辑有缺陷吗？



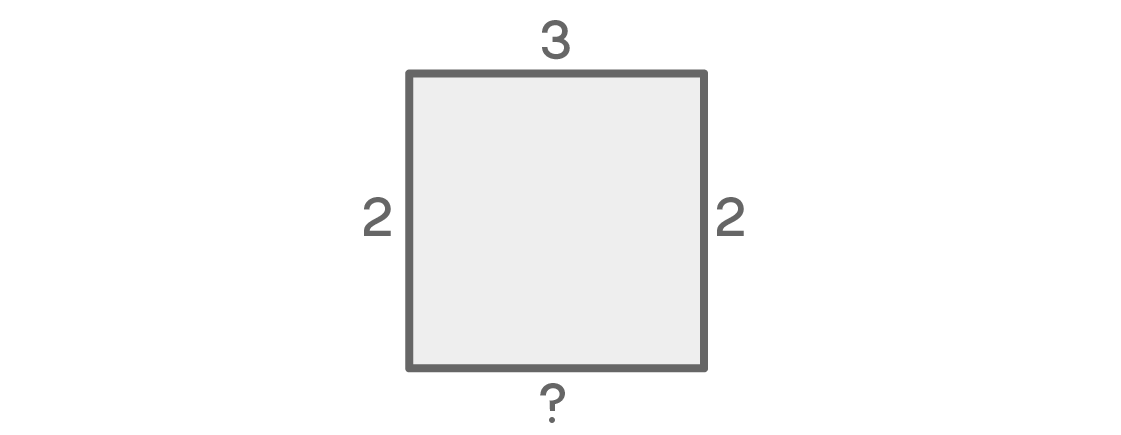
实际上，如果左右位置具有不同的颜色，则对于底部位置将只有一个选择。 例如，如果在左侧为蓝色，而在右侧为红色，则底部必须为黄色。 但是，如果左右颜色相同，该怎么办？ 在这种情况下，对于最底层的位置，将有两个选择。 最后的选择取决于先前的选择，这使我们的计算复杂化。

我们必须考虑两种不同的情况：左侧和右侧的颜色重合时以及它们不同时。

如果左右两侧的颜色重合，则每个位置的可能性数如下所示：



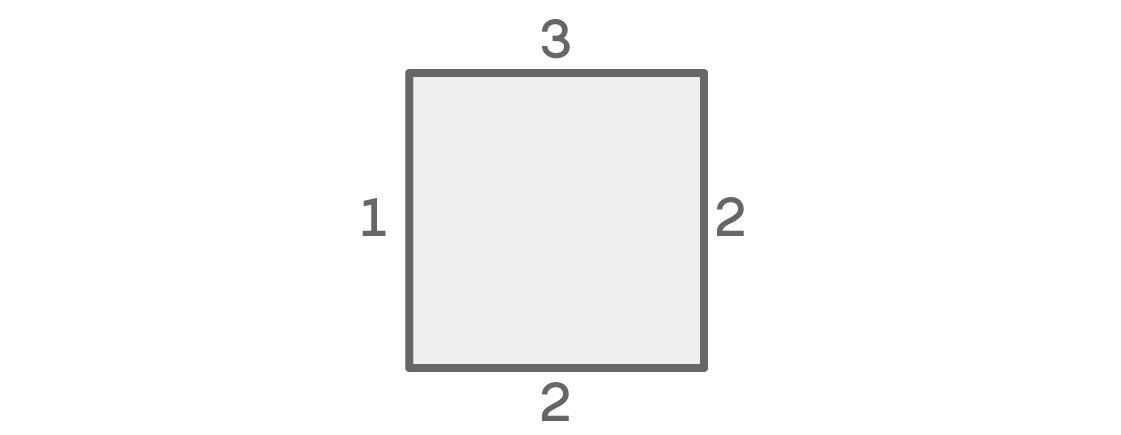
对于上层座位，我们有三个选择。 左边有两个。 由于我们假设左右位置具有相同的颜色，因此，左位置只有一个选择：与右边相同的颜色。 最后，由于左右颜色相同，因此我们可以为下排座椅选择其余两种颜色中的一种。 结果，我们得到3×2×1×2 = 12个可能的座位安排。

现在让我们看一下左右颜色​​不同时的可能性：



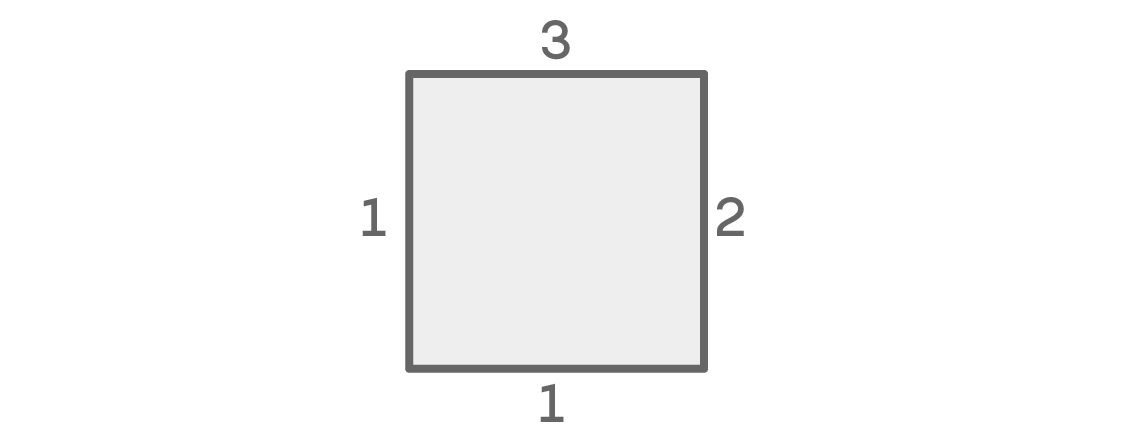
我们再次为顶部提供了三个选项，为正确的位置提供了两个选项。 左边的地方还是有一个选择，但是有一个不同的原因：根据我们的条件，它不能与顶部，相邻地方相同，也不能与右边相同。 并且，由于左右的颜色不同，所以底部仅剩一个选项（与顶部相同）。 这种情况给出了3×2×1×1 = 6种可能的排列方式。

由于这两个选项涵盖了所有可能性，因此我们将它们加起来并得到12 + 6 = 18个可能的座位安排。

添加第三种颜色会使我们的任务复杂化，但是我们的辛勤工作将得到回报。 现在我们可以对4、5或任意数量的不同颜色的q使用此策略。

无论颜色多少，我们总是有两种情况：左和右将是相同或不同的颜色。 假设我们可以选择q种颜色。 下面的图表显示了左右颜色相同的情况下每侧的选项数量：



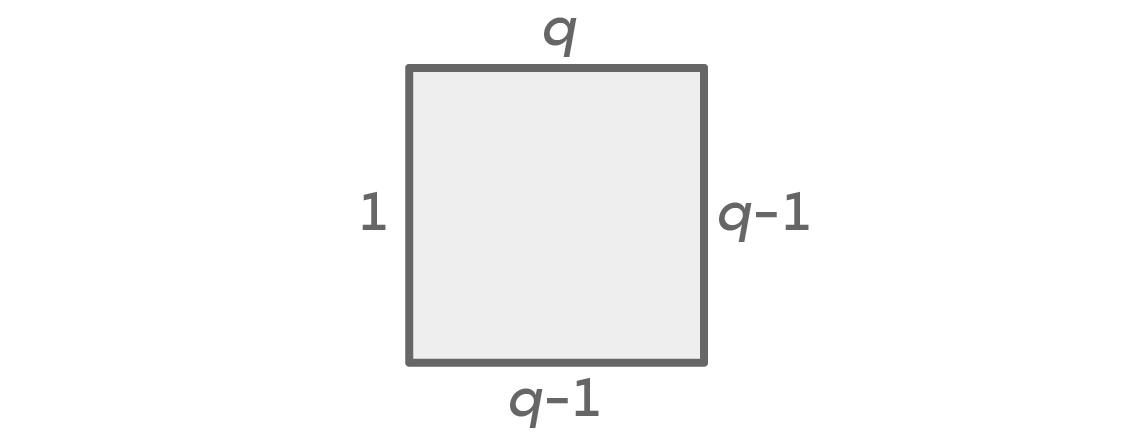
首先，我们为上座使用q颜色，右边为q-1。 由于我们假定左右的颜色相同，因此对于左颜色我们只有一个选择。 剩下的q-1个选项用于底端斑点，因为它可以是我们为左右两侧斑点选择的颜色以外的任何颜色。 计算的基本原理为我们提供了q×（q-1）×1×（q-1）= q（q-1） ^2种可能的布局。

如果左右位置的颜色不同，那么我们可以计算出如下可能性：



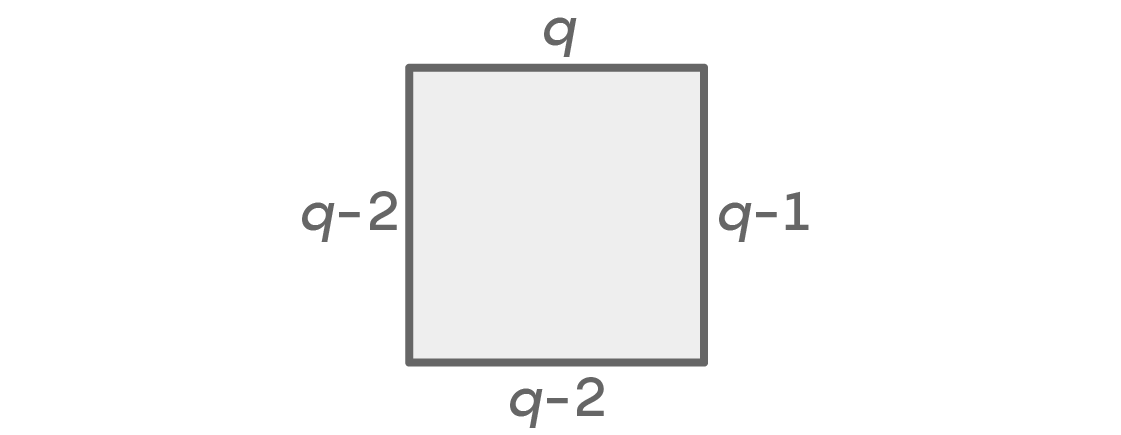
同样，我们在顶部有q个选项，在正确的地方有q-1个选项。 左上方和右上方选择的颜色不能相同，因此有q-2选项。 下面可以有任何颜色，除了我们左右使用的两种颜色外，这再次提供q-2选项。 我们得出的总和为q×（q-1）×（q-2）×（q-2）= q（q-1）（q-2） ^2个可能的座位安排。 由于这两种情况涵盖了所有选项，因此，像以前一样，我们将它们加起来并得到可能的排列总数：q（q-1） ² + q（q-1）（q-2） ² 。

这样的表述似乎是对以下问题的奇怪回答：“在方形桌子上，不同团队有多少种不同的座位安排，以致同一团队的两名成员不会并排坐着？” 但是，此多项式包含许多有关我们的问题的信息。 他不仅给了我们定量的答案，而且还揭示了我们任务的结构。

这样的多项式称为“ 色多项式 ”，因为它回答了以下问题：存在多少种方法可以对网络（或图形）的顶点进行着色，以使任何一对相邻的顶点具有不同的颜色？

最初，我们的问题与桌子周围的座位有关，但我们可以轻松地将其转变为有关为图形的顶点着色的问题。 代替餐桌旁的人：



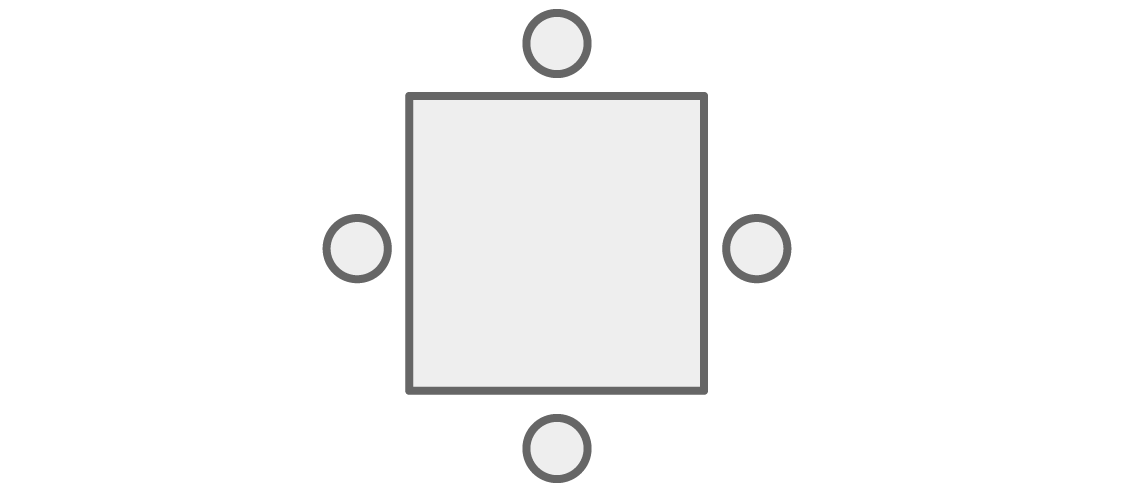
我们可以想象它们以峰顶形式存在，当它们位于旁边时，它们之间由边缘相连。



现在，图的顶点的任何颜色都可以表示为正方形周围的人的座位，其中表的“坐在旁边”意味着图上的“具有共同的边缘”。

现在，以图的形式重新表达了我们的问题，我们回到了色多项式。 我们称它为P（q）。

P（q）= q（q-1） ² + q（q-1）（q-2） ²

该多项式的显着特性是，它回答了任何数量可能的颜色的着色问题。 例如，要回答三种颜色的问题，我们将q = 3，得到：

P（3）= 3（3-1） ² + 3（3-1）（3-2） ² = 3×2 ² + 3×2×1 ² = 12 + 6 = 18

这是我们在三支队伍中得到的答案。 如果我们把q = 2：

P（2）= 2（2-1） ² + 2（2-1）（2-2） ² = 2×1 ² + 2×1×0 ² = 2 + 0 = 2

听起来很熟悉？ 这是我们有两个团队的第一个谜语的答案。 我们可以找到四个，五个甚至十个不同团队的答案，只需将q的期望值替换为：P（4）= 84，P（5）= 260和P（10）=6570。色多项式抓住了问题的一些基本结构通过总结我们的计数策略。

通过对多项式P（q）= q（q-1） ² + q（q-1）（q-2） ²进行代数运算，可以揭示结构的更多细节：

= q（q-1）（q-1）+ q（q-1）（q-2） ²
= q（q − 1）（（q − 1）+（q − 2） ² ）
= q（q − 1）（q − 1 + q ² −4q + 4）
= q（q − 1）（q ² −3q + 3）

我们从总和的每个部分中提取因子q（q-1）并组合相似项，从而将多项式简化为因式分解形式。 并且以这种形式，多项式可以借助其“根”告诉我们有关结构的信息。

多项式的根是输入值，在输出处它等于零。 查找因式分解形式的根更加容易：由于多项式表示为乘法部分，因此任何一个因子等于0的值都会重置整个乘积。

例如，我们的多项式P（q）= q（q-1）（q 2-3q + 3）有一个因数（q-1）。 如果取q = 1，则该因子等于零，就像整个乘法结果一样。 也就是说，P（1）= 1（1-1）（1 2-3×1 + 3）= 1×0×1 =0。类似地，P（0）= 0×（–-1）×3 = 0因此，q = 1和q = 0是我们多项式的根。 （您可能对系数（q 2-3q + 3）感兴趣。由于对于任何实数q都不等于零，因此它不会给我们的色多项式提供新的根。）

这些根在图的框架内是有意义的。 如果我们选择相同的颜色，则每个顶点必须具有相同的颜色。 无法为图形着色，以使所有相邻的顶点具有不同的颜色。 正是这意味着q = 1是我们的色多项式的根。 如果P（1）= 0，则有零种方法可以使图形着色，从而使相邻顶点的颜色不同。 对于零个颜色数（P（0）= 0）的版本也是如此。色多项式的根告诉我们图形的结构。

如果考虑其他图，通过代数查看结构的能力将变得更加明显。 让我们看一个三角图：



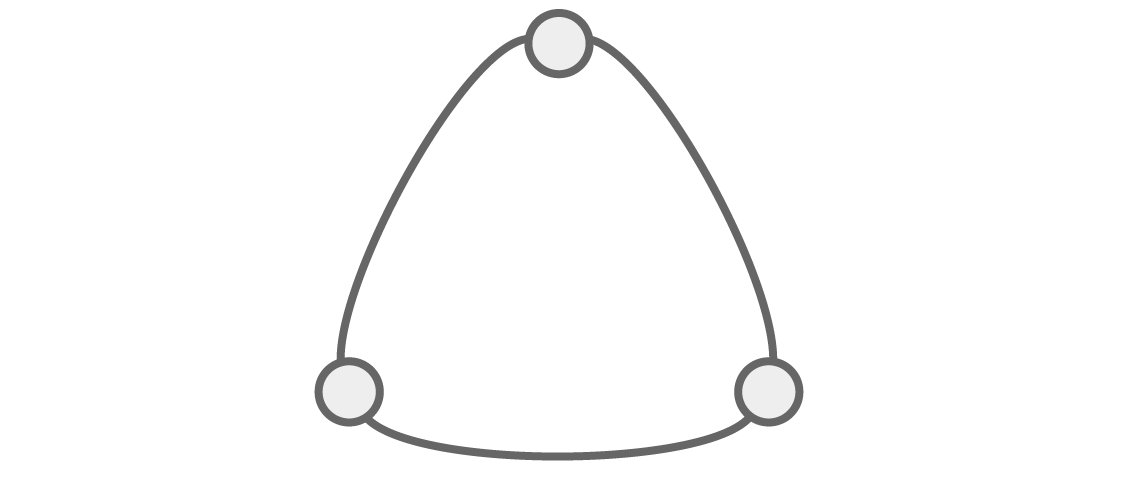
有多少种方法可以对此图q上色，以使相邻顶点不是相同颜色？

像往常一样，对于前两个相邻顶点，有q和q-1选项。 而且由于最后一个顶点与前两个顶点相邻，因此它们的颜色应该与前两个顶点不同，这使我们有了q-2个选项。 这给了我们这个三角图的色多项式：P（q）= q（q-1）（q-2）。

通过这种分解形式，这个色多项式告诉我们一些有趣的事情：它的根q = 2。 并且，如果P（2）= 0，则应该不可能用两种颜色对此图形进行着色，以使其不具有相同颜色的两个相邻顶点。 是这样吗

想象一下，我们在这个三角形中走一圈，沿途给山峰上色。 如果只有两种颜色，则需要在每个顶点之后进行交替：如果第一种是红色，则第二种将是蓝色，这意味着第三种应该再次是红色。 但是第一个和第三个峰是相邻的，并且它们都不能都是红色的。 正如多项式所预测的，两种颜色是不够的。

使用类似的交替参数，我们可以得出一个重要的概括：具有奇数个顶点的任何闭环的色多项式的根必须等于2。由于如果您交替两种颜色并沿奇数长度的环移动，则第一个和最后一个有色顶点将是相同的颜色。 但这就像是一个循环，它们将相邻。 无法着色。

例如，我们可以使用各种技术来确定对于具有五个顶点的循环，色多项式看起来像这样：P（q）= q 5-5q ⁴ + 10q 3-10q ² + 4q。 考虑到这一点，我们得到P（q）= q（q-1）（q-2）（q2-2q + 2）。 正如预期的那样，结果证明q = 2是根，P（2）=0。有趣的是，一旦我们发现了图及其多项式之间的这种联系，想法就开始在两个方向上起作用。 多项式可以告诉我们有关图的结构的信息，而图可以告诉我们有关多项式的结构的信息。

正是对结构的寻求促使June Ho证明了Reed关于色多项式的40年假说。 假设指出，如果我们按顺序枚举色多项式的系数，而忽略它们的符号，则将满足以下条件：任何系数的平方必须至少是两个相邻系数的乘积。 例如，在我们的五顶点循环的色多项式中，P（q）= q 5-5q ⁴ + 10q 3-10q ² + 4q，我们看到5 2≥1×10、10 2≥5×10和10 2≥10×4。例如，由此得出结论，并非每个多项式都可以是彩色的：与图关联的彩色多项式具有更深的结构。 此外，这些多项式与其他域之间的联系使Ho和他的合著者在证明Reed假设几年后，可以回答与Roth假设有关的更广泛的问题。

多项式可能以最差的形式而闻名-作为代数表达式形式运算中的抽象练习。 但是多项式及其性质-根，系数，各种形式-有助于揭示意想不到的地方的结构，并在我们周围的所有事物中与代数建立联系。

练习题

1.完整图是一个图，每对顶点通过一条边连接。 找到五个顶点的完整图的色多项式。


2.找到下一个图的色多项式（使用有关较简单图的色多项式的信息）。




3.如果一个图的顶点可以分为A和B两组，则该图被称为两面的，因此A的顶点仅与B的顶点相邻，而B顶点仅与A的顶点相邻。假设图G的色多项式为P （q）。 哪些属性P（q）可以使您得出结论，图形G是双面的？