互联网上有许多文章介绍了梯度下降算法。 将会有另一个。
1958年7月8日, 《纽约时报》写道 :“一位心理学家展示了旨在阅读并变得更明智的计算机的雏形。 海军开发的……价格704美元的计算机,耗资200万美元,经过五十次尝试学会了区分左右……根据海军的说法,他们使用这一原理建造了Perceptron类的第一台思维机,可以读写。 开发计划在一年内完成,总成本为100,000美元。科学家预测,以后的感知器将能够识别人并用名字称呼他们,立即将口头和书面讲话从一种语言翻译成另一种语言。 罗森布拉特先生说,从原则上讲,有可能建立可以在装配线上重现自己并知道自己存在的“大脑”(引自S. Nikolenko的书,“深度学习,沉浸在神经网络世界中”)。
啊,这些记者知道如何吸引人。 弄清楚什么是Perceptron类的思维机真的很有趣。
对象的二进制(二进制)分类,感知器类的人工神经元
这是我们的人工神经元,它将对象分为两类(执行对象的二进制分类):

因此,我们有:
- 输入:采样对象-m维空间向量 X = (X 1 ,。。。,X m )
- 重物 瓦特= (瓦特1 ,。。。,W m ) 一个用于样本对象的每个特征(也是一个m维向量)
- 内部:加法器 S U M = w 1 x 1 + 。。。+ w m x m = s u m m j = 1 w j x j -神经元输入的加权和
- 下一步:激活 Φ(x,w)=Φ(总和)
- 更进一步:量化器(阈值)-θθ
- 激活+阈值-基于神经元输入(对象属性)的加权和预测对象的类别标签。 这部分定义了神经元的特定架构。
- 输出:对象类标签(两个之一) \ hat {y} = \ {1,-1 \}\ hat {y} = \ {1,-1 \}
分类 -因为神经元将一个类分配给对象,所以是binary ( binary )-因为只有两种可能的类。
\帽子y [带盖游戏]-我们将表示对象的预测(计算)类值 x
y [无盖常规游戏]-对象的真实(已知)类值 x 从训练集中
价值观 x (以下 x 和 w -这些不是单位值,但向量因对象而异,权重系数不同 w (一旦选择)保持不变。 对于每个对象的训练集 x 类标签已知 y 。 在训练阶段,您需要选择权重 w 使模型产生正确的值 \帽子y (正好与 y ),以获取训练集中的最大对象数。 以这种方式训练的神经元的有用性的假设是基于这样的希望,即它将以选定的系数产生正确的值 \帽子y 对于新对象 x 真正的阶级价值 y 事先未知。
神经元输入的加权总和的直观含义是对象的所有属性(每个符号都是神经元的输入之一)会影响对象分类的结果,但并非所有符号都会受到同等影响。 在多大程度上确定重量; 将某个加权系数归零会使相应属性对总量的贡献无效,即 这无异于从对象中删除特征。
自适应线性神经元ADALINE
ADALINE神经元(自适应线性神经元)是具有以下激活功能的普通人工神经元:
Φ(x,w)=Φ(总和)=总和
\ Phi(x ^ {{(i)},w)= \ Phi(\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {{i)})= \ sum _ { j = 1} ^ {m} w_ {j} x_ {j} ^ {{i}}
以下标 我 方括号中将表示 我 训练集的要素 x(i) 或真正的阶级价值 y ^ {{i)} 或预测的类别价值 \ hat {y} ^ {{i)} 为他。
可以说,这样的神经元根本就没有激活功能,输入加权和的值被馈送到量化器的输入(阈值)。 但是出于一致性考虑,将加权和的值视为激活值将更为方便。
阈值(量化器)-预测类标签:
\ hat {y} ^ {{(i)} = \左\ {\开始{矩阵} 1,\ Phi(x ^ {{{i)},w)\ ge \ theta \\-1,\ Phi(x ^ {{(i)},w)<\ theta \ end {matrix} \ right。
如果激活值大于某个阈值θθ,则量化器将标签“ 1”分配给对象;如果激活值小于阈值θ,则对象接收标签“ -1”。
在这里,我们可以将问题近似表示 :我们需要选择神经元的参数
这样的阶级价值观 \帽子 由神经元分配给训练样本的对象,与类的真实值一致 y 对于相同的元素(或至少给出了大多数的正确含义)。
我们对阈值函数进行一些转换,以类为例 \帽子y=1 并将阈值转移到不等式的左侧:
\开始{聚集} \ Phi(x ^ {{(i)},w)\ ge \ theta \ hfill \\\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {( i)} \ ge \ theta \ hfill \\-\ theta + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 \ hfill \\ \ end {聚集}
表示 w0=− theta 和 x0=1
\开始{聚集} w_ {0} x_ {0} ^ {{(i)} + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {{i}} \ ge 0 ,w_ {0} =-\ theta,x_ {0} = 1 \ hfill \\\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {{(i)} \ ge 0, x_ {0} = 1 \填充\结束{聚集}
如我们所见,我们设法摆脱了单独的参数θ,以新的权重系数为幌子将其引入 w0 在总和的符号下,同时在对象的描述中添加新的虚拟单元符号 x0=1 。
我们将考虑新符号来更正问题的表述。
任务' :选择神经元加权因子的参数 wj,j=0,..,m ,
x0=1 (符号常数)- 虚拟神经元( 置换神经元 )
从这个地方开始,我们将符号和权重c编号为0,而不是1。 w 我们将说它大约是(m +1)维,而不是m维。 向量 x 根据上下文,我们可以考虑(m +1)维(在公式中大部分情况下),但请记住实际上它是m维的。
为何是神经元( 在我们的案例中,这不是神经元,而是对象或输入的信号,但是在多层网络的情况下,它变成神经元,通常称为这种方式 ) 为什么是虚构的 -现在很清楚。 为什么他还会流离失所,将在稍后阐明。
现在用总和激活如下所示:
\ Phi(x ^ {{(i)},w)= \ Phi(\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {{i)})= \ sum _ { j = 0} ^ {m} w_ {j} x_ {j} ^ {{i)},x_ {0} ^ {{i}} = 1 \ forall i
现在,阈值始终为0(零)(实际值已移至参数 w0 ):
\ hat {y} ^ {{{i}} = \左\ {\开始{矩阵} 1,\ Phi(x ^ {{{i)},w)\ ge 0 \\-1,\ Phi(x ^ {{i}},w)<0 \ end {matrix} \ right。
我们再次用另一种措辞来表述问题(问题的几何含义)
如果仔细查看激活函数的公式,我们将看到它是(m + 1)维空间中的参数超平面,而在前m个维中,它与样本元素的点共存,并且(m + 1)- e维-与元素分开的函数值的空间。
现在,如果我们将激活值等于零(阈值),那么这也将是一个超平面,仅在m维空间中,即 完全在元素值空间中 x 。 此超平面将分隔元素。 x 分为两个不相交的组。
通常在这个地方,他们说我们的任务是选择参数值 w ,即 在元素的空间中构造一个m维超平面,以使训练集的值为“ 1”类的元素位于平面的一侧,而值为“ -1”的元素在另一侧。
对于那些不太理解这里写的内容的人,请继续阅读-现在我们都将看到,这是第一位。 其次,我们还将看到,这种问题的陈述虽然有效,但并不完全完整。
一维空间(m = 1)
这是代码开始出现的地方。 我们使用常规的Matplotlib库构建所有图,但是在这里我还使用Seaborn库在一行中来调整图的面积,因为 我喜欢她的做法,但原则上您可以没有她。
我们采用许多一维点并对其进行回答:
import numpy as np import math
在这里,我们拥有数组X1的第i个元素-这是训练样本的第i个元素(第i个点)(更确切地说,它是第一个也是唯一的属性): x(i)=(X1[i]) , x(i)1=X1[i]
数组y的每个第i个元素都是正确答案,这是与带有单个属性X1 [i]的训练样本的第i个元素相对应的真实标签。
我们只取5分,前两个分给“ -1”级,其余三个分给“ 1”级。
在线上画出这些点:
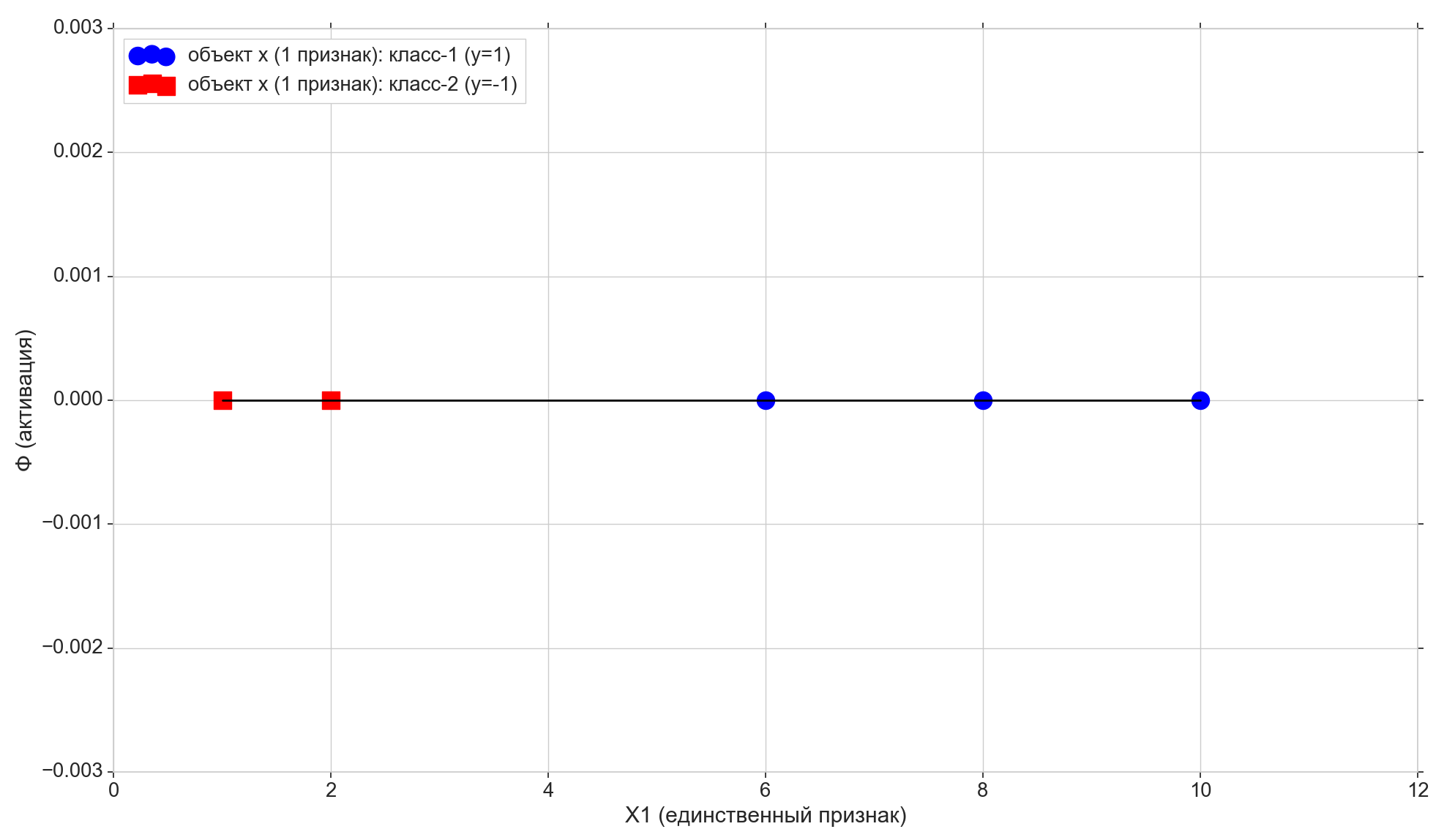
现在让我们看一下激活函数:
Phi=w0+w1x1
如您所见,这是平面上的一条普通参数线(在二维空间,即(m +1)维空间中):
- 在水平轴上,我们有元素的点(它们也是属性X1的值)
- 在垂直方向上-每个元素的激活值
- 参数 w1 -设置倾斜角度,
- 但是 w0 -沿垂直轴移动(这是剪切神经元的答案)。
w0 = -1.1 w1 = 0.4

还记得在进行少量转换后,我们的激活阈值变为零。 因此,如果第ith个元素在激活线上的投影小于零,我们将-1类分配给该元素( \帽子y=−1 ),如果它大于零,我们将类别分配为“ 1”( \帽子y=1 )
紫色点-激活线与轴的交点 Phi=0 ,将元素从不同的类别中分离出来,这是在1维(即m维)特征空间中构建的非常分离的超平面(对于1维空间,点是超平面)。 如您所见,将元素划分为组就足够了,但是为了将类分配给组,就不够了。 为了将类分配给元素,我们需要在2-d空间(即,在(m + 1)-d)“符号+激活”中建立直接的(二维超平面)激活:激活方向与垂直方向的偏离轴将确定元素组的类,因为 这取决于激活时元素的投影是高于还是低于零。
修改参数 w0 和 w1 我们将收到不同的激活行。 我们需要建立这样的激活线,即 找到这样的参数组合 w 训练样本的前两个点在激活线上的投影低于零(对于它们,值 \帽子y=y=−1 ),其余3个点的投影将在零以上(对于它们 \帽子y=y=1 )
很明显,在我们的特殊情况下,构造这样的线没有什么复杂的,而且,这样的线通常可以构造成无数个。 但是,我们将尝试以满足某些最优性标准(可能影响未来预测的质量)的方式构建它,并且还应该具有将算法扩展到多维案例的能力。
在这里我们还注意到,我们特别选择了初始的点集,以便可以用这样一条线划分点(对于1-e:第一组的所有元素都较小,第二组的所有元素都大于某个固定值),即 许多训练点是线性可分离的 。
向图上再添加两条与类{1,-1}相对应的水平线,并将元素投影到它们上。

底线为“ -1”类的点 \披=−1 ,将“ 1”类项目指向顶部 Phi=1 。
让我们注意另一个细微差别。 我们沿着垂直轴绘制激活值,激活值的空间是连续的。 但是分类器的结果(通过阈值的激活函数)是两个元素{-1,1}的离散集合,而不是连续的标度。 在这里,我们采取一组离散的类 y 并把它放在一个连续的激活规模上 \皮皮 因此离散类值成为激活量表上的普通点-激活值的特殊情况,它可以直接接受或接近它们。 严格来说,最初我们不能将数值作为类别,而应将字符串标签“ class-1”和“ class-2”作为类别,在这种情况下,我们必须将字符串标签与激活等级上的数值匹配。 因此,在我们的情况下,不应将类“ -1”和“ 1”的值直接用作类标签,而应将其标记为激活级。
是时候输入错误指标了

很自然地接受到,所选元素的激活值与同一元素的类值越接近,激活类对该元素的预测就越好。 因此,对于选定元素的错误,您可以采用两点之间的距离-元素在激活线上的垂直投影和元素在其已知(true)类的水平线上的投影。 在图形上:错误-橙色垂直线。
成本(亏损)功能
对于每个单独的项目,我们都有一个错误指标。 我们可以从中获得整个激活线的质量指标。 例如,很自然地接受到,训练样本的所有元素的错误总和越小,我们建立的激活线就越好。 对于每个单独的元素,误差不会很小,但是对于整个训练样本,您可能会有所妥协。
但是,您不能接受简单的错误总和,而可以接受平方误差的总和(平方误差的总和,平方误差的总和,SSE )。 很明显,就普通误差的总和而言,激活线越接近具有真实元素类别的点,则二次误差的总和就越小,但是在二次误差的情况下,最远的元素将受到更严厉的惩罚。
实际上,这里让我们感兴趣的不是远方元素的罚款金额,而是二次函数具有最小值并且可在任何地方微分的事实(通常的总和将具有最小值,但在此最小值将不会微分),看看为什么这样做是必要的。过一会儿。
因此:
- 错误-从类标签值到激活超平面的距离
- SSE-训练样本所有元素的二次误差之和
- 成本函数 J(w) -所选激活线的质量指标。 值越低,激活越好。
作为价值的函数 1\超过2 在线性神经元的一般情况下,SSE如下所示:
\ begin {gathered J(w)= {1 \ over 2} SSE = {1 \ over 2} \ sum _ {i = 1} ^ {n}(\ Phi(\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {{(i)})-y ^ {{i}})^ {2} = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {{i}}-y ^ {{i}})^ {2} \ end {gathered}
( 1\超过2 首先,它不会干扰SSE,其次,为了方便起见,它将进一步降低美观)
在这里 我 -元素编号,以及 n -训练集中的元素数量。 让我提醒你 y ^ {{i)} -真正的阶级 我 训练样本的元素,即 事先知道正确答案。
我们记得,激活线的位置取决于参数-加权因子 w 因此向量 w 充当损失函数的参数。
对于一维情况
J(w)=1 over2SSE=1 over2 sumni=1(w0+w1x(i)1−y(i))2
价值观 x 和 y 预先已知(这是一个训练集),因此它们是固定的。 我们选择参数 w ,即 w0 和 w1 这样的价值 J(w) 原来是最小的。 让我们尝试将图形绘制为值 J(w) 取决于参数 w0 和 w1

通常,在这里已经可以看到损失函数具有最小值,并且近似位于该位置。 但是,让我们再做一个技巧,并仅使用对数垂直标度构建相同的图形。

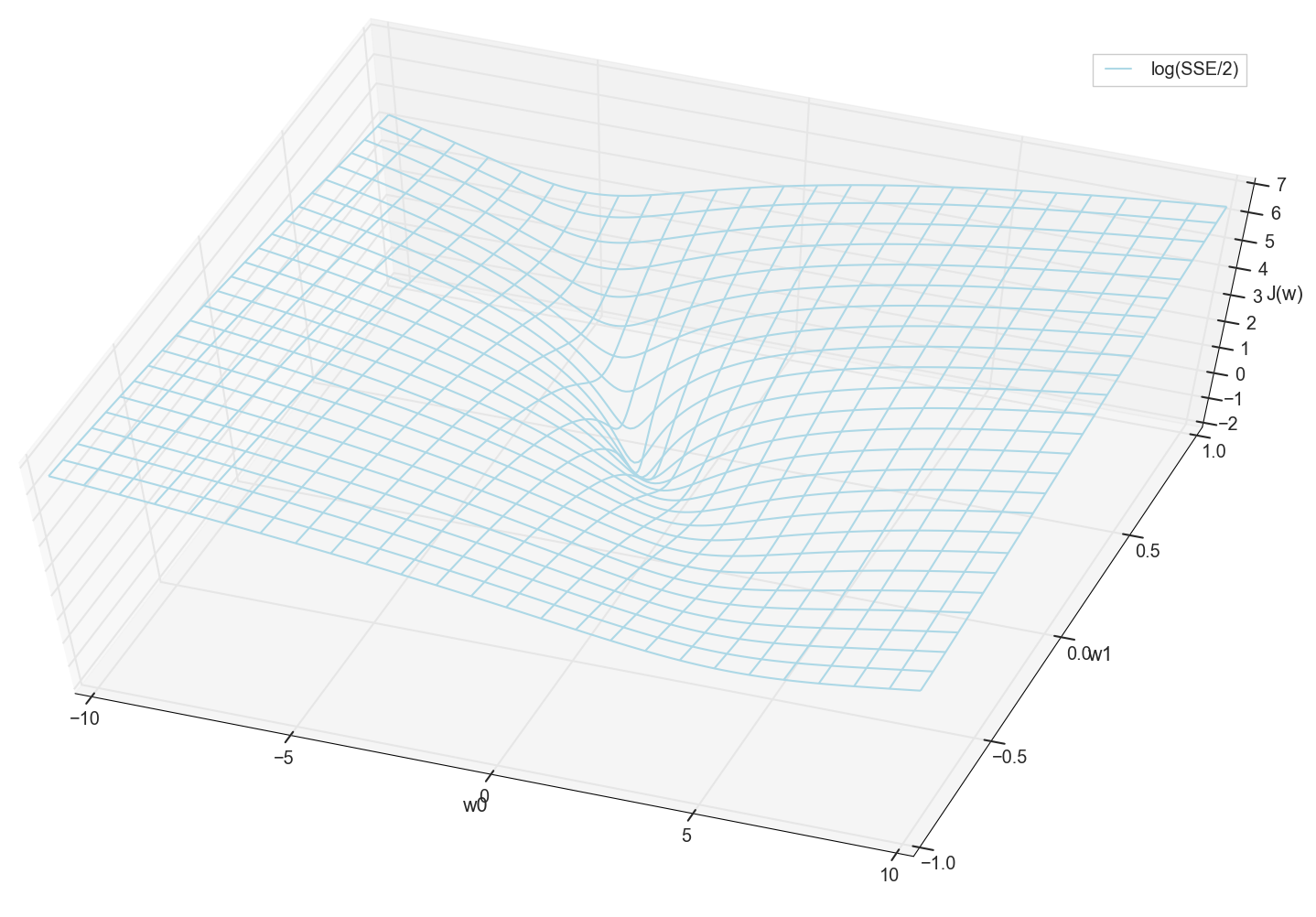
我不了解您,但是就我个人而言,当我第一次看到这张图表时,我得到了启发。 这种自然的腔体不仅仅是神经网络上一篇流行文章中多维山丘的图形化可视化,它是真实的图形。
我们的任务是选择这些值 w0 和 w1 到达这个坑的底部。 我们得到权重的值-我们得到训练有素的神经元。
由于我们都是一样地绘制图形并亲自观察其最小值,因此没有人会禁止我们通过“手动”在网格上进行简单的枚举来找到其坐标:

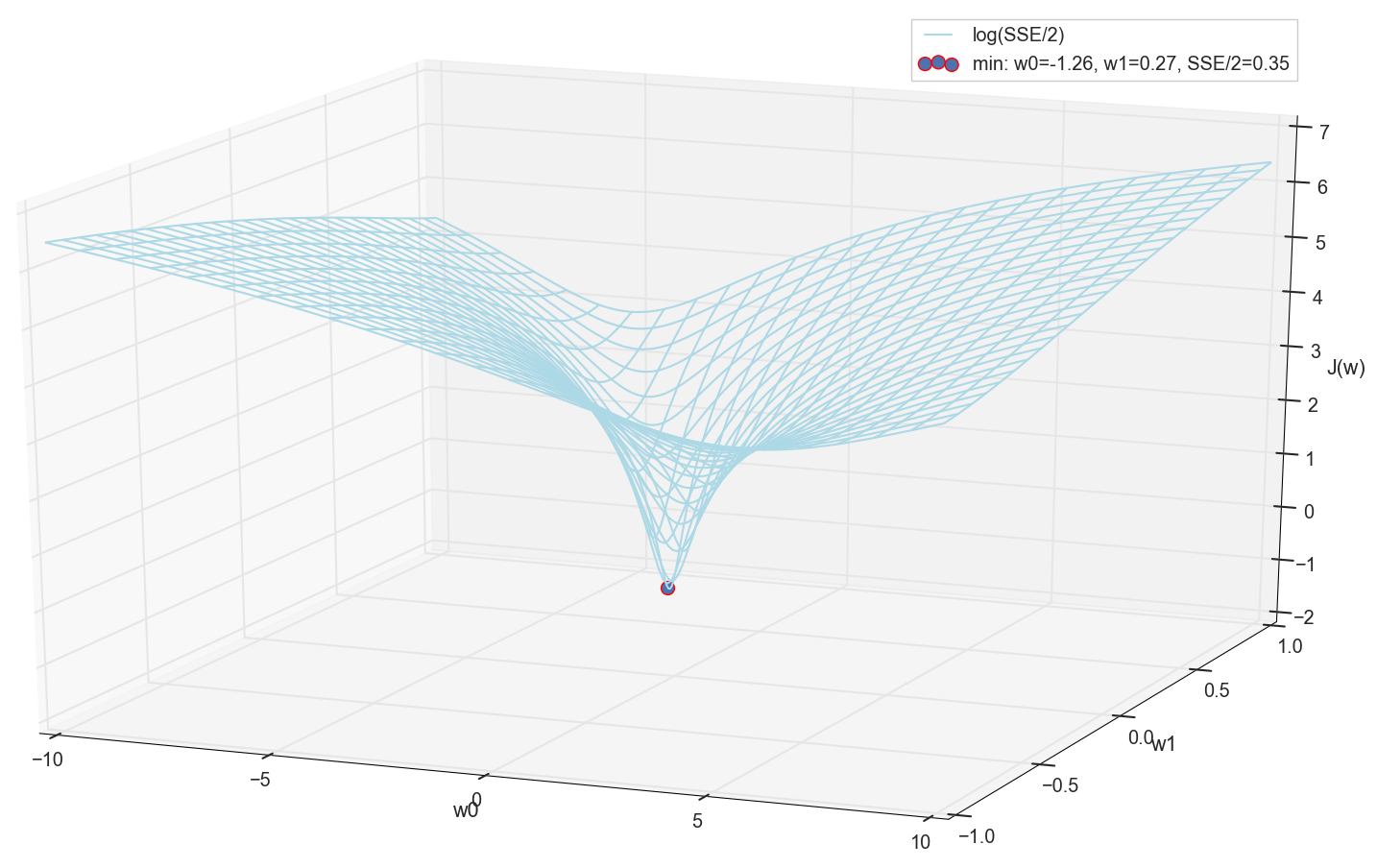
这些是值: w0=−1.26 和 w1=0.27 ,上证所的平方误差之和为0.69,成本函数 J(w)=SSE/2=0.35 (更精确地:0.3456478371758288)。
让我们看看使用这些参数激活的外观:

对我来说,这很正常。 激活与零阈值的交点将元素从不同的类别中分离出来,激活本身为它们分配正确的值。 同时,激活似乎处于某个最佳位置。
在继续之前,我们再次钦佩网格上的图形:
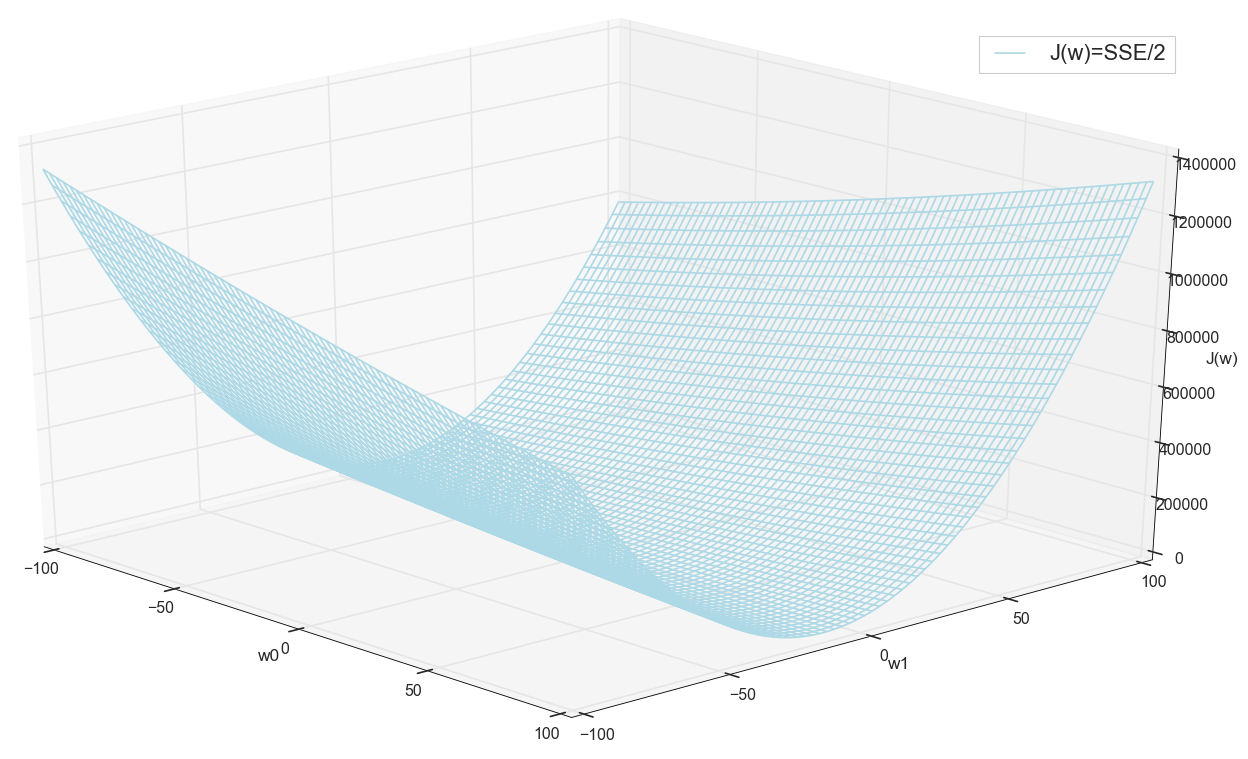
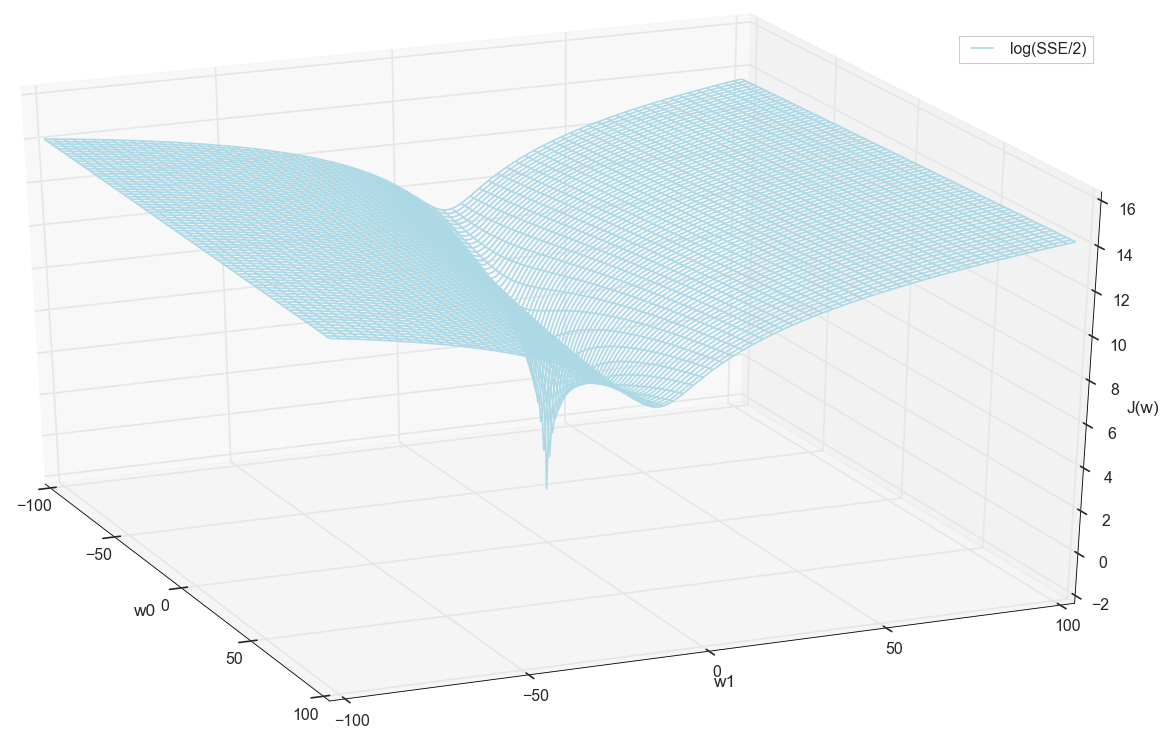
似乎附近没有其他人会想到的。
最小搜寻
因此,我们得到了权重-最小误差值的坐标。 这将是训练样本上权重的最佳值。 一般来说,这正是我们所需要的,可以说神经元是经过训练的。 也许可以完成?
搜索最小值:按网格搜索
- 乍一看,该选项相当有效(如我们所见)
- 您需要事先知道要寻找最小值的区域(可以使用较大的边框,然后缩小搜索范围-仅凭眼睛即可)
- 为了提高准确性,您需要减少步数→甚至增加点数(解决方案:您可以迭代地缩小搜索范围)
- 点太多(对于2d来说可能没问题,但是对于多维情况,我们很快就会遇到资源)
- 对于MNIST(28x28 = 784像素-相同的输入数量,相同的加权因子加偏移量,每维100步的网格):100 ^ 785 = 10 ^ 1570。
因此,如果我们想通过在每次测量100点的网格上通过直接枚举搜索最小值来在28x28 = 784像素的图像中训练单个神经元(甚至不是神经网络),则需要整理出10 ^ 1570个组合。 对于存储和搜索来说,这是很多东西(在宇宙的可见部分中只有10 ^ 80个原子,宇宙存在约4 * 10 ^ 17秒= 4 * 10 ^ 26纳秒)。
让我们尝试更快地找到一个选项。
最小搜索:恒定步降
让我们看一下损失函数的图形 J(w) 在飞机上:修复 w0 改变 w1
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
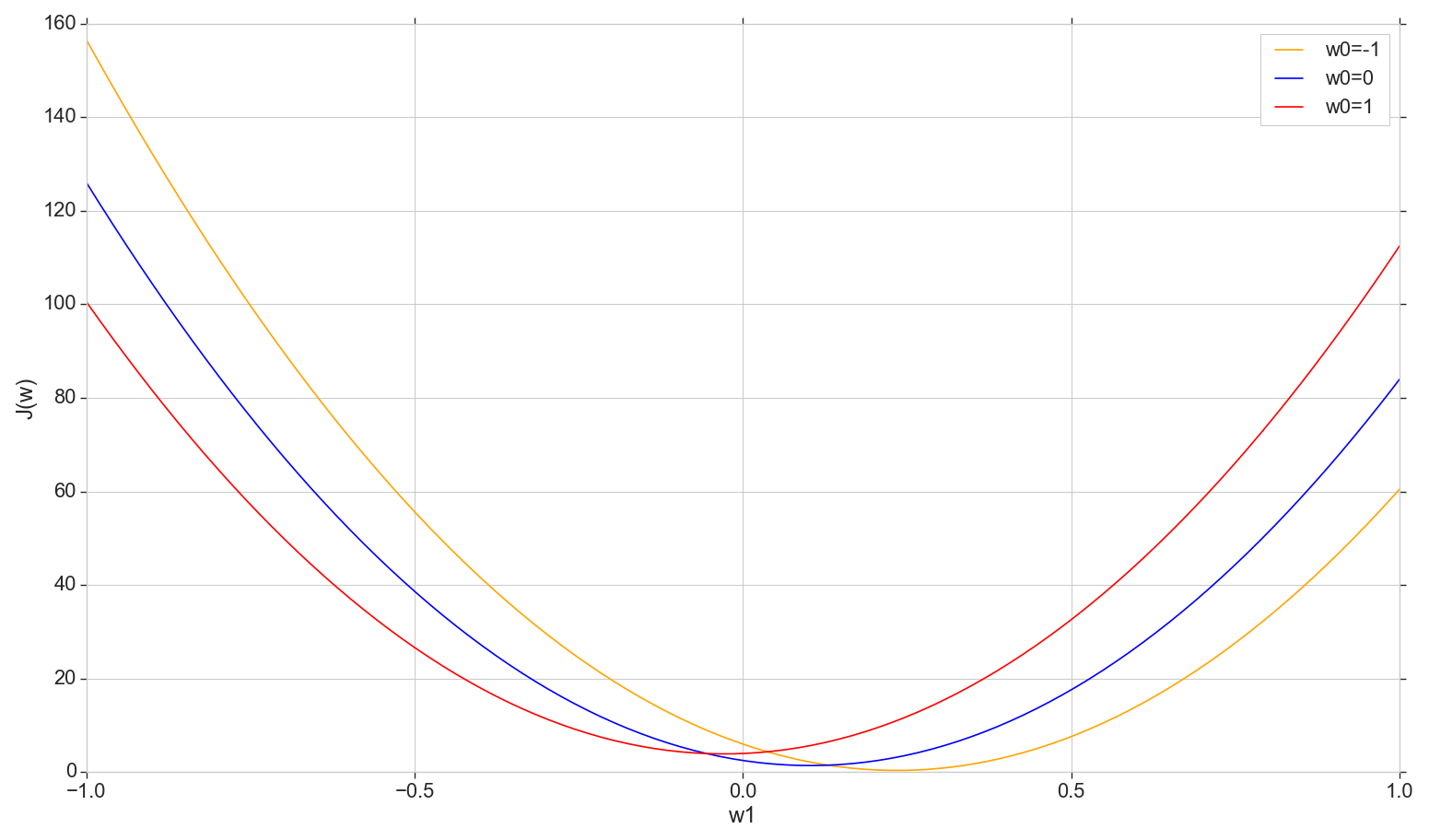
这是一个普通的抛物线(更确切地说是一个抛物线族-根据固定的价值类型,它们会略有不同 w0 ) 要找到最小的抛物线,不必对所有点进行分类。 我们可以在水平轴上选择一个任意点,然后逐步移动到最小点。
考虑恒定螺距选项
- 如果步长太大,您可能会错过,而无法达到最小值(可以减少步长)
- 如果太小,步骤将太多(可能会更多)
- 在任何情况下,我们都不会达到精确的最小值,但是我们可以通过将步长更改为找到的不准确的最小值附近(步长不再恒定)来实现任意精确度
- 我们不知道下降的方向(可以通过算法解决:不要逐步增加误差)
- 查找范围的问题已解决(您可以从任何地方掉下来-迟早我们都会掉下来)
- 原则上,该选项有效,但也许有更好的选择?
注意:当我谈到降级的选择时,一位学生问,如果您可以立即使用公式找到最小抛物线,为什么要逐步移动? 首先,我本着我们现在对考虑迭代选项感兴趣的精神回答了一些问题,以便以后我们不仅可以将其与抛物线一起使用,还可以在其他情况下使用。 另外,实际上,我们在本节中至少不需要抛物线-我们将移至最低限度,而不是仅在一个维度上,而是在所有维度上移至最小,这样,在每次新迭代中,就不会沿着该抛物线进行新的步骤,而是抛物线具有新的值偏移的切片 w0 。 但是后来考虑,我认为,原则上说,如果我们不按步调动每个切片,而是立即向下滚动到当前切片的最小值,那没有错。 因此,一次又一次地进行逐次测量,我们仍然必须滑落到全局最小值,并且它似乎比步骤要快。 对于单个神经元,它应该起作用,而不仅仅是抛物线起作用。 但是我还没有开始浪费时间测试这个理论,所以在这里我们继续-我答应谈论梯度下降。
搜索最小值:梯度下降
总的来说,我们会走下坡路,但是我们会更明智地做到这一点。 我们使用成本曲线的导数来选择步骤(此处不是成本曲线 ,而是成本曲线 )。
- 我们有几个维度,每个维度都有自己的曲线:我们修复了所有问题 wj 除了 wk ,
- J(wk) 会有误差曲线 k 维度
- 所有这些(在我们的情况下)都是抛物线,但是总的来说,重要的是它们在任何地方都可以微分并且具有最小的
- 为了调整每次测量的步长,我们将使用误差函数相对于该测量的偏导数(变化系数 wk )
- 这种偏导数的向量称为梯度。
一切都很好,但是衍生品从何而来呢? 现在让我们弄清楚。
导数的几何含义
对我来说,很长一段时间以来,导数仍然是一组特殊的公式和计算规则,另外还涉及到增加,减少和极限。 在这里回忆或找出实际的导数是合适的。
微分函数 y(x) 在这一点上 x0 是函数的增量比例的极限 Deltay 自变量递增 Deltax 在增加参数时 Deltax 趋于零:
y′(x0)= lim Deltax\到0 Deltay over Deltax, Deltay=y(x0+ Deltax)−y(x0)

图片中的圆点 M(x0,y(x0))=(x0,y0) 是我们要确定导数的点。 点数 N(x0+ Deltax,y(x0+ Deltax))=(x0+ Deltax,y0+ Deltay) -通过增加参数获得的点 Deltax 。 直达 Mn -割线穿过这两点。
点数 -割线的交点 Mn 带水平轴 y=0 。
考虑两个直角三角形:一个三角形 \三角形NPM 带割线 Mn 作为斜边和三角形 \三角形MBA 与割线到轴的延续 y=0 -细分 AM 作为斜边。 从图形和学校几何学课程可以明显看出 \角度NMP 和 \角MAB 相等,因此它们的切线相等:
tan\角度MAB= tan\角度NMP=MB AB上的=NP MP上的= Deltay over Deltax
添加到图片: MD - 与该点的初始曲线相切 M 越过轴 y=0 在这一点上 D 。 三角形 \三角形MBD -带有斜边的直角三角形-盒形截面,扇形 MD 。
我们瞄准增量 Deltax 归零:
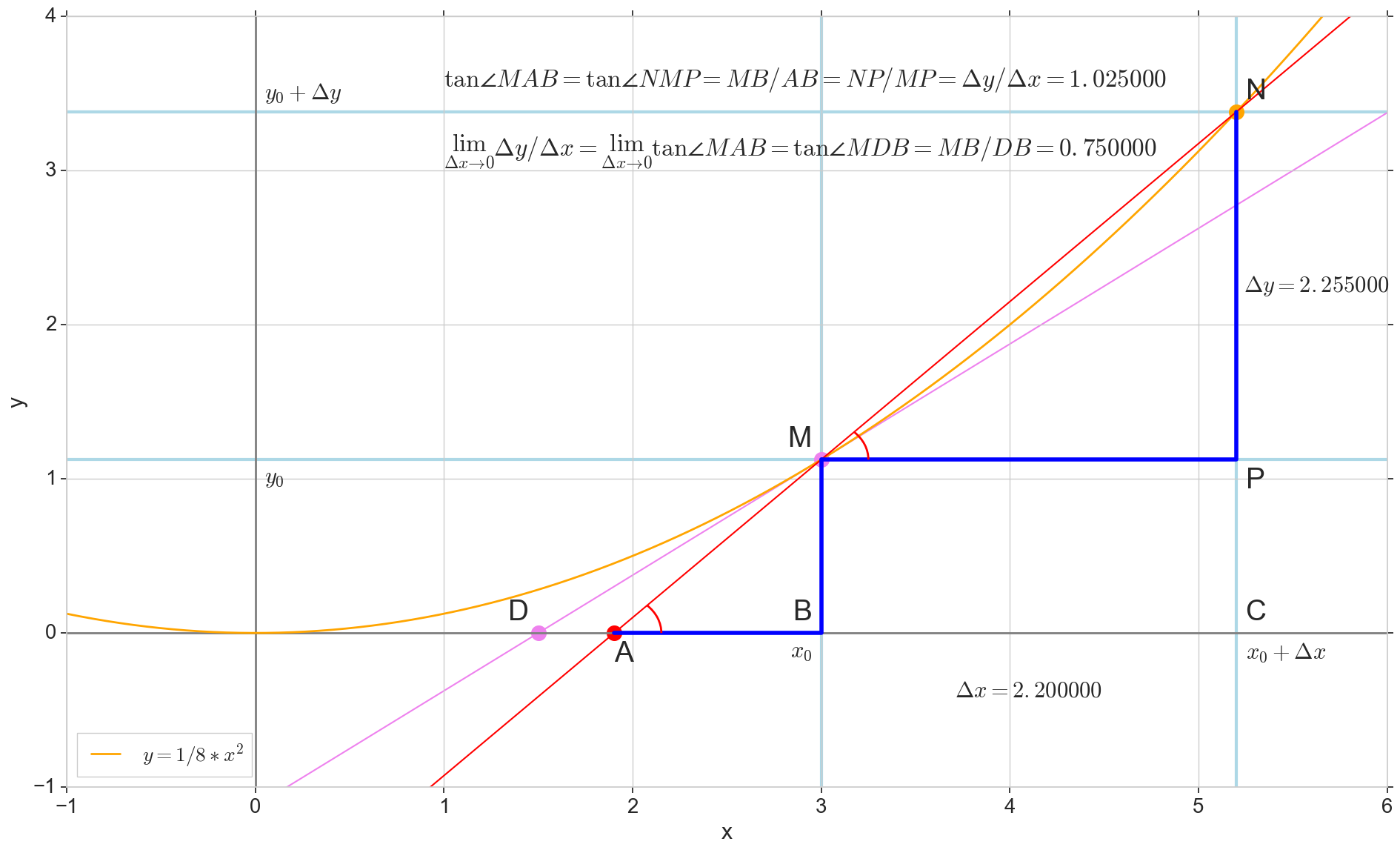
点数 N 移至重点 M 按功能,点 爬行到一个点 D 沿轴 y 正割 Mn 变成切线 MD 带触点 M 。 源三角形 \三角形NPM 带腿 Deltax 和 Deltay 缩小到一个点,但是像这样的三角形 \三角形MBA 变成一个三角形 \三角形MBD 不仅保持宏观尺寸,而且保持角度相等 \角MAB 和 \角度NMP 。
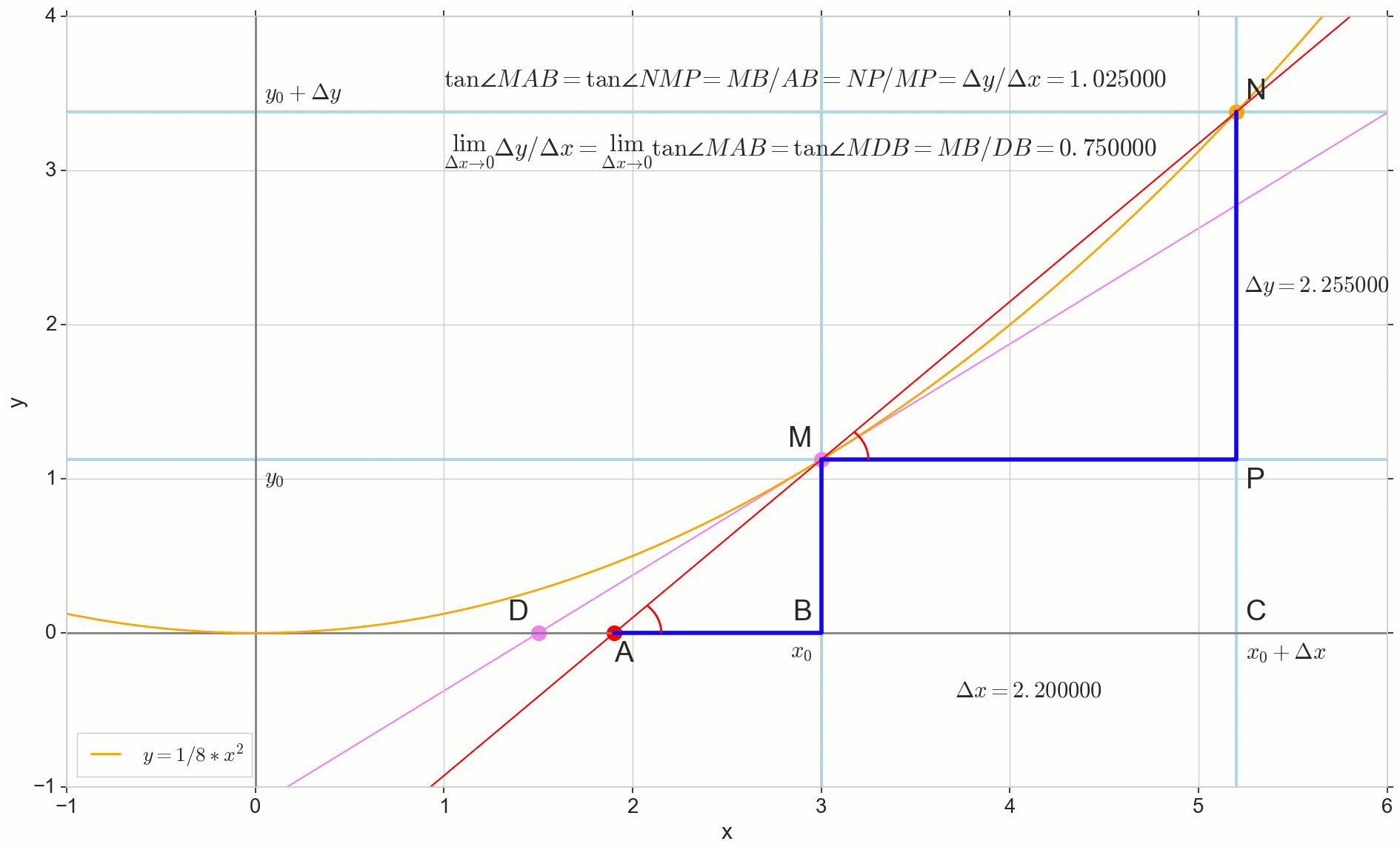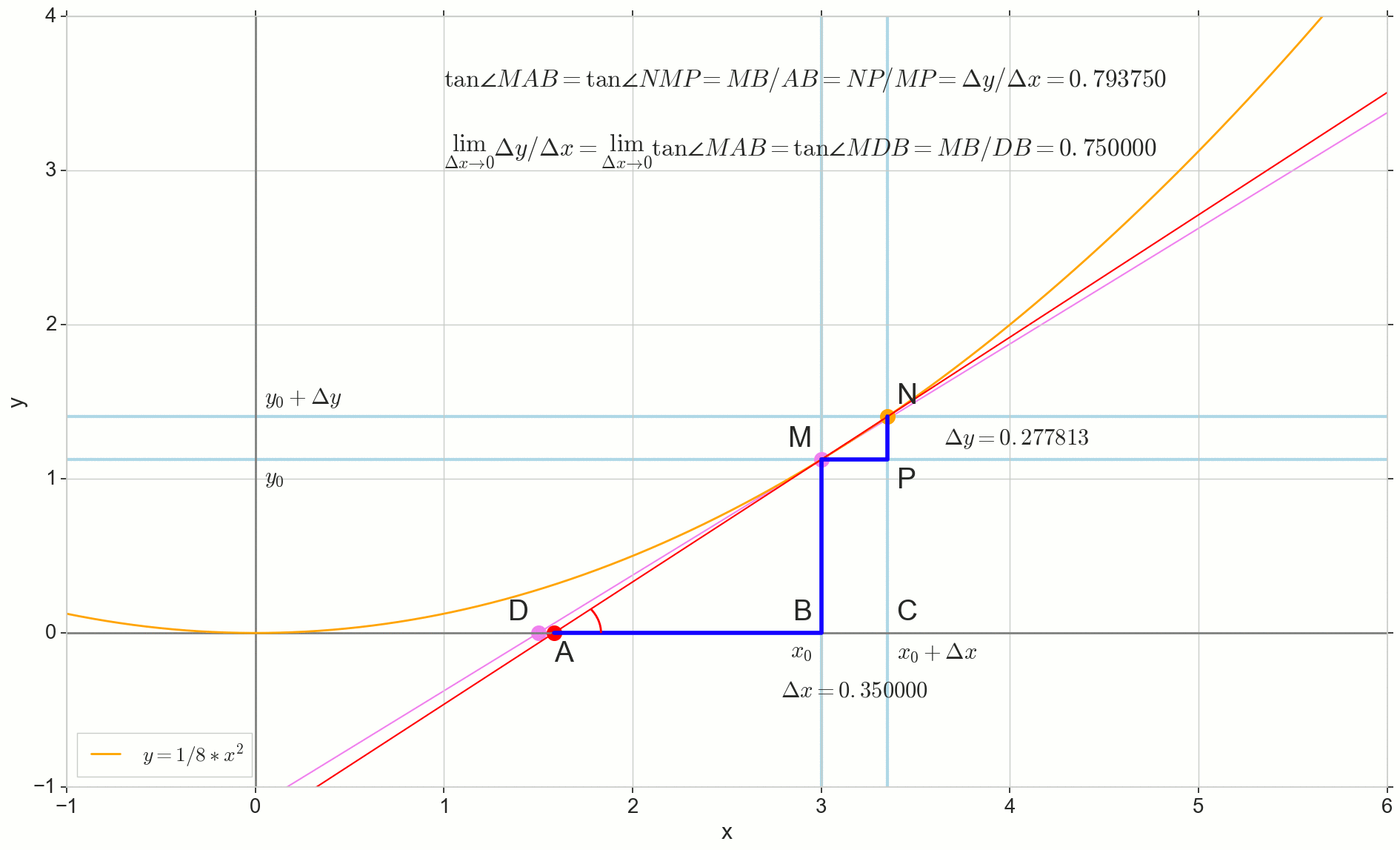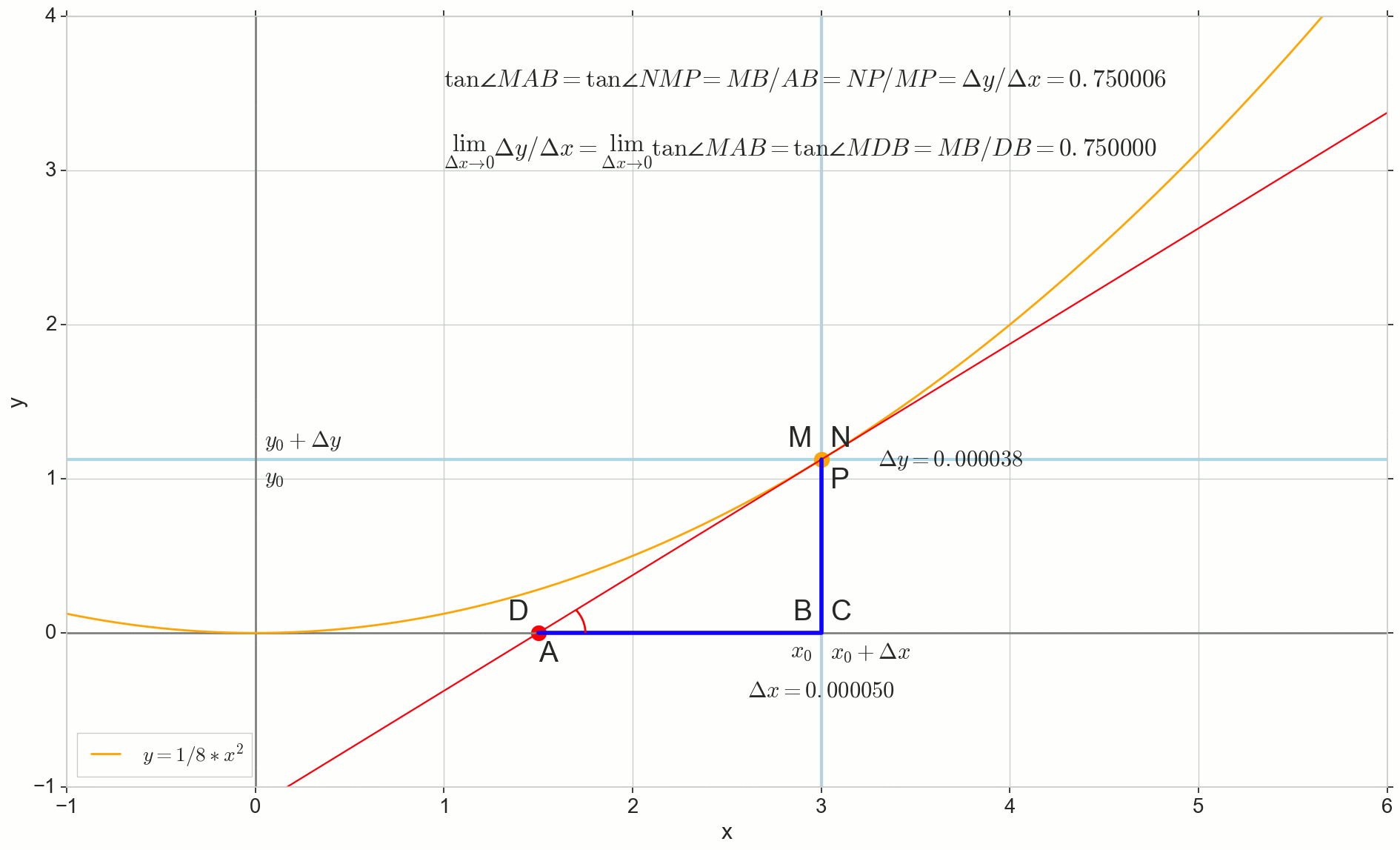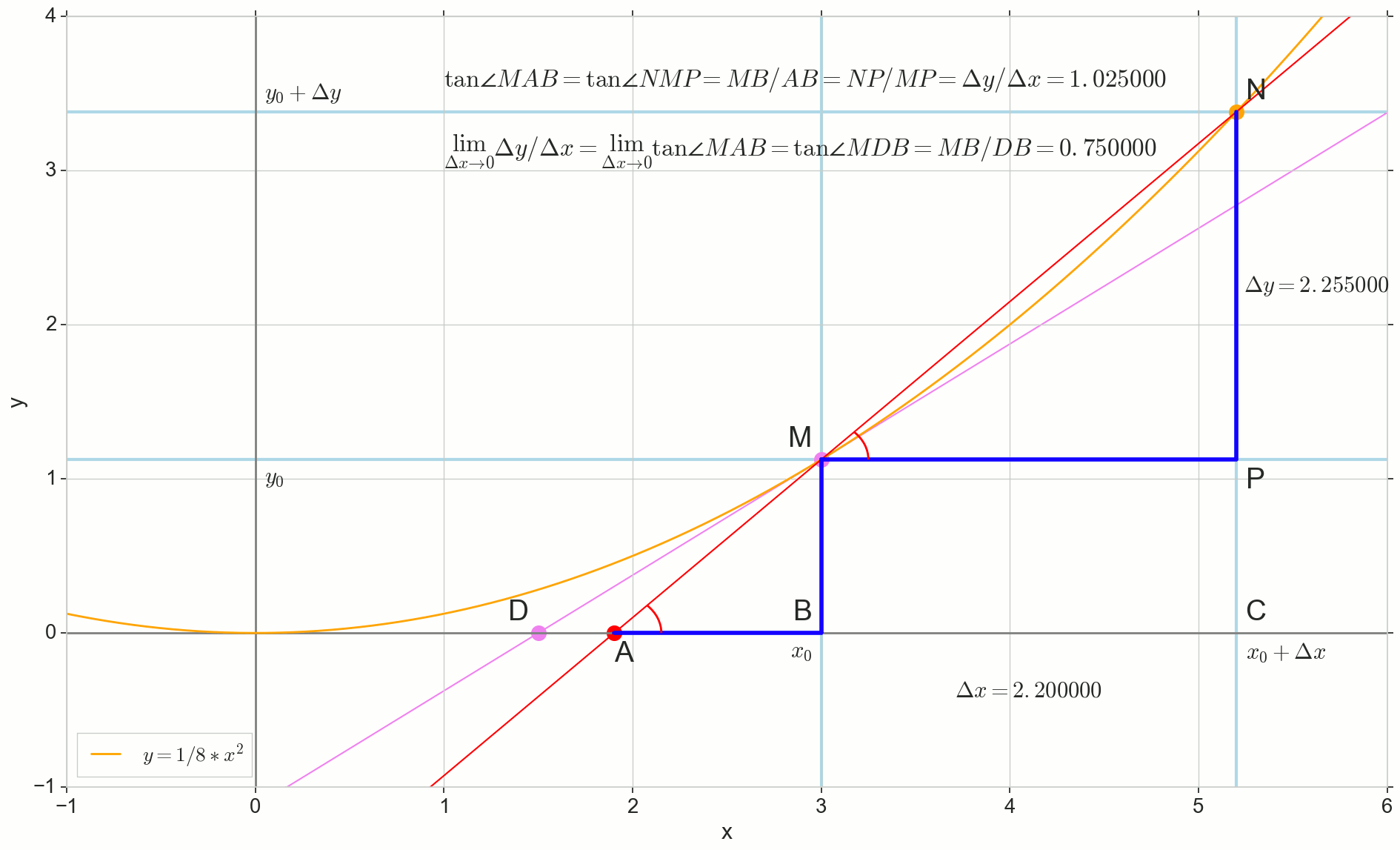
如何增加 Deltax ,无限接近零,将永远不会达到零,因此 N 永远不会到达确切的位置 M 点 不会达到重点 D 三角形 \三角形MBA 不会变成 \三角形MBD 。 , , «» lim 。
△MBA — △MBD , :
limΔx→0ΔyΔx=limΔx→0tan∠NMP=limΔx→0tan∠MAB=limΔx→0MBAB=MBDB=tan∠MDB
:
limΔx→0ΔyΔx=tan∠MDB
, , :
y′(x0)=limΔx→0ΔyΔx=tan∠MDB
, y=0 。 .
, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).
:
- x0 y=0
- — y(x0) — x0 y=0 y=0
- «» , ,
- — : — , —
- ( , , , Δy )
, , :

— , — x0 , — . — — . — y=0 , — .

, , , , . ( , ) (: y=0 , ).

( ): , (: y=0 , ).
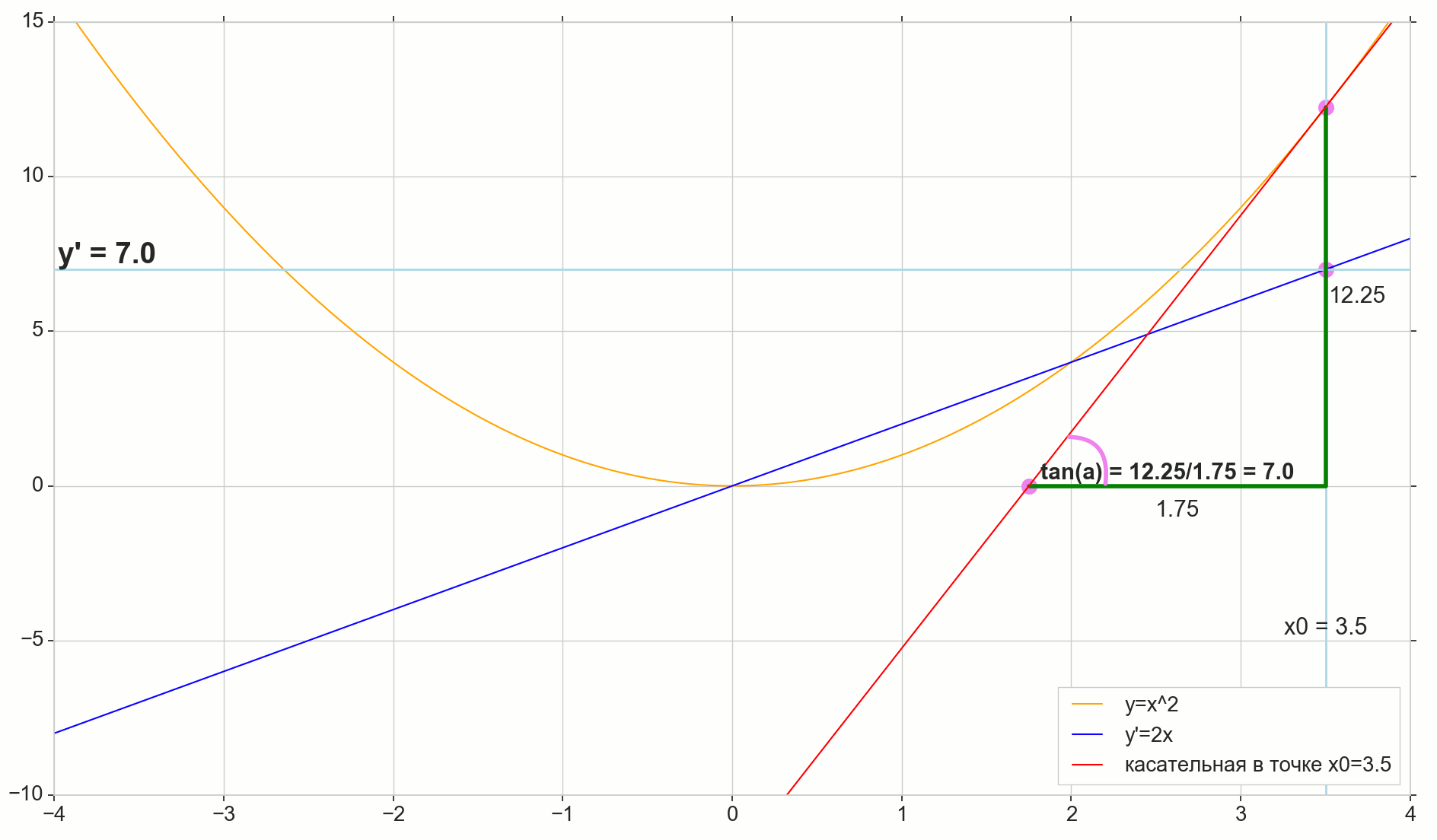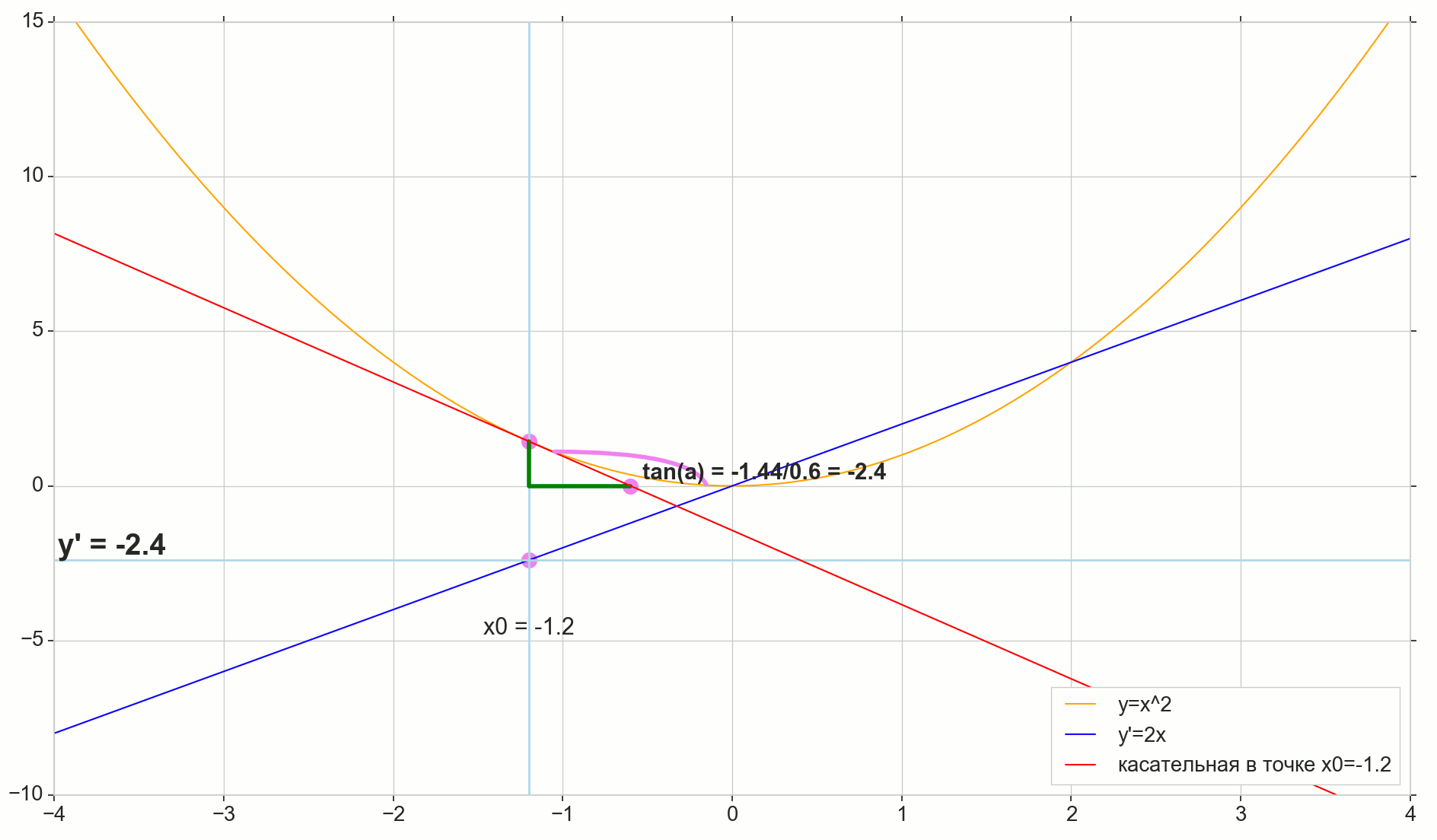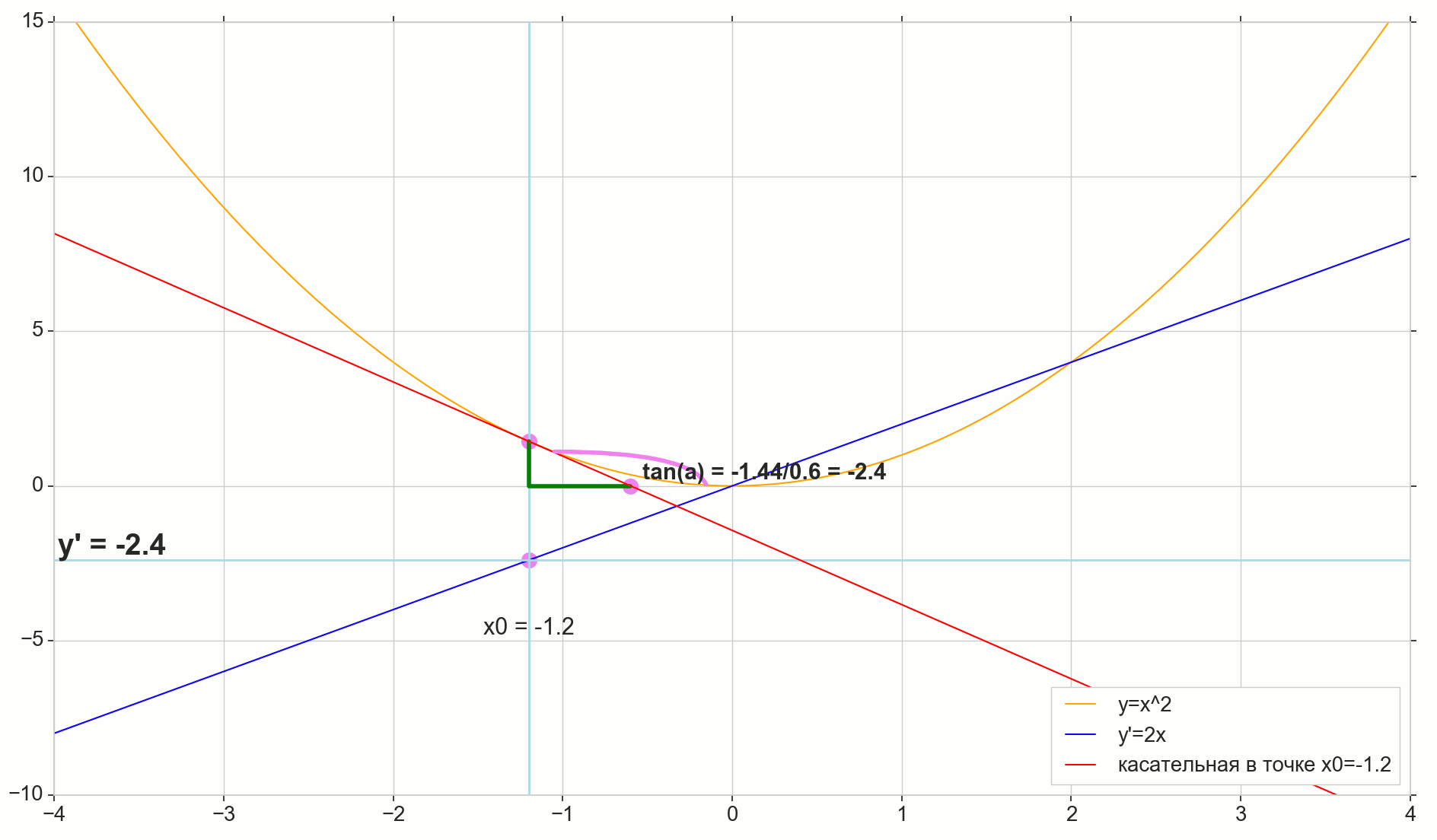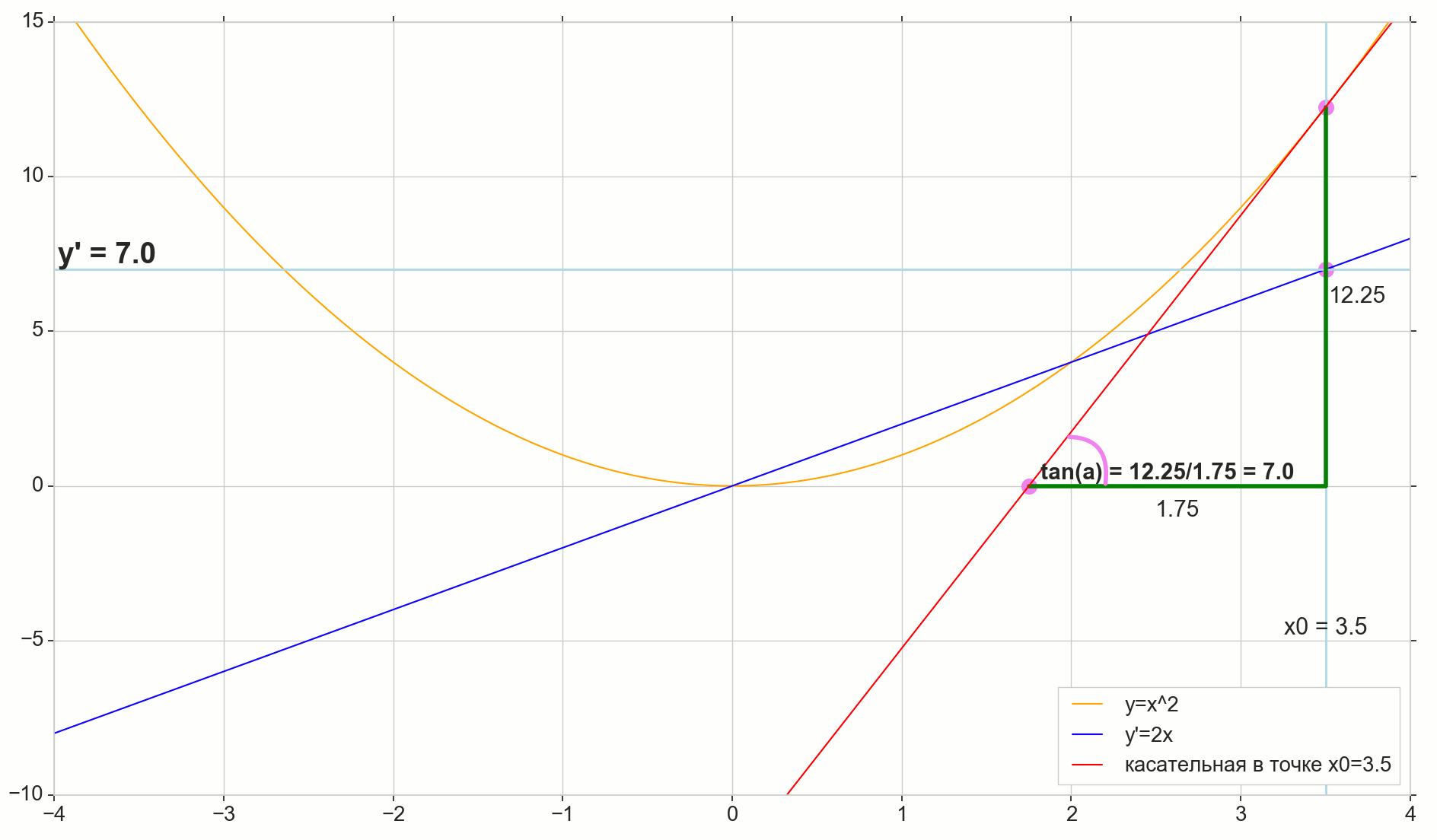
, : (), «»/«» , . — . , , ? .
J(w) 。 , , , .
J(w)=12SSE=12n∑i=1(m∑j=0wjx(i)j−y(i))2
∂J(w)∂wk=∂∂wk12n∑i=1(m∑j=0wjx(i)j−y(i))2=12n∑i=1∂∂wk(m∑j=0wjx(i)j−y(i))2=12n∑i=12(m∑j=0wjx(i)j−y(i))∂∂wk(m∑j=0wjx(i)j−y(i))=122n∑i=1(m∑j=0wjx(i)j−y(i))∂∂wk((w0x(i)0+...+wkx(i)k+...+wmx(i)m)−y(i))=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
, : , , , ( ) . , wk ( , ), . , , , 1/2 SSE .
:
∂J(w)∂wk=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
— ( ∇ [], , .. []):
∇J(w)=(∂J(w)∂w0,...,∂J(w)∂wm),w=(w0,...,wm)
:
w:=w+Δw,Δw=−η∇J(w)
k - :
wk:=wk+Δwk,Δwk=−η∂J(w)∂wk
:
, , , . , .
1- :
Φ(x,w)=w0+w1x1
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1−y(i))x(i)0=n∑i=1(w0+w1x(i)1−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1−y(i))x(i)1
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1−y(i))x(i)1
, . .
( w1 )
w0=1 , J(w1)
X ( ) y w0 和 w1 ( ):
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
w1 -1.5 1.5.
, ( , , ):
plt.subplot(3,1,1)

, , δJ(w)δw1 — :
grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left')

Δw1(w1) (, Δw1 w1 , .. , ):
eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right')

plt.show()

- : ,
- : — «» ( , «» ),
- : — ( ), η [] ( ),
: , 1000 .
, ,
w — - - . w0=1 , w1=0.9 。 η=0.001 ( , ) 12:
:
w1 J(w1,w0=1) :
Δw1(w1)
plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u' , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange')

, , ( ), . , , , .
: , , , «» , — , .
- — w1 , —
- , w1
- — : , —
- , —
- , ( ), , ( ) — , —
- ( , — ).
- : — , —
- ? — . .
- . w1 , . , «»/«» . , , . , , , « ». , : w1=0.9 200, , , , 1. , , , . — η 。 , 200 1. η=0.001 , w1=0.9 200*0.001=0.2 ( -1, -0.2) — .
- J(w1=0.9)=92.43 , 12 (, ) J(w1=0.03)=8.54
- , ,
, . , . , ( , ). η , .
: , , , .
, , , .
η
- η [] — ()
- ,
- «»: , , ,
- , J(w)
- : wk , η , wk
η=0.01

. , . 3- , 3- , , .. , .. . , , [] .
η J(w) η

: , , . , — , , .
:

:

.
η 。 , , .

, .
:
, ( ) w , , . , , , . , , .
,
, .
, :

— :
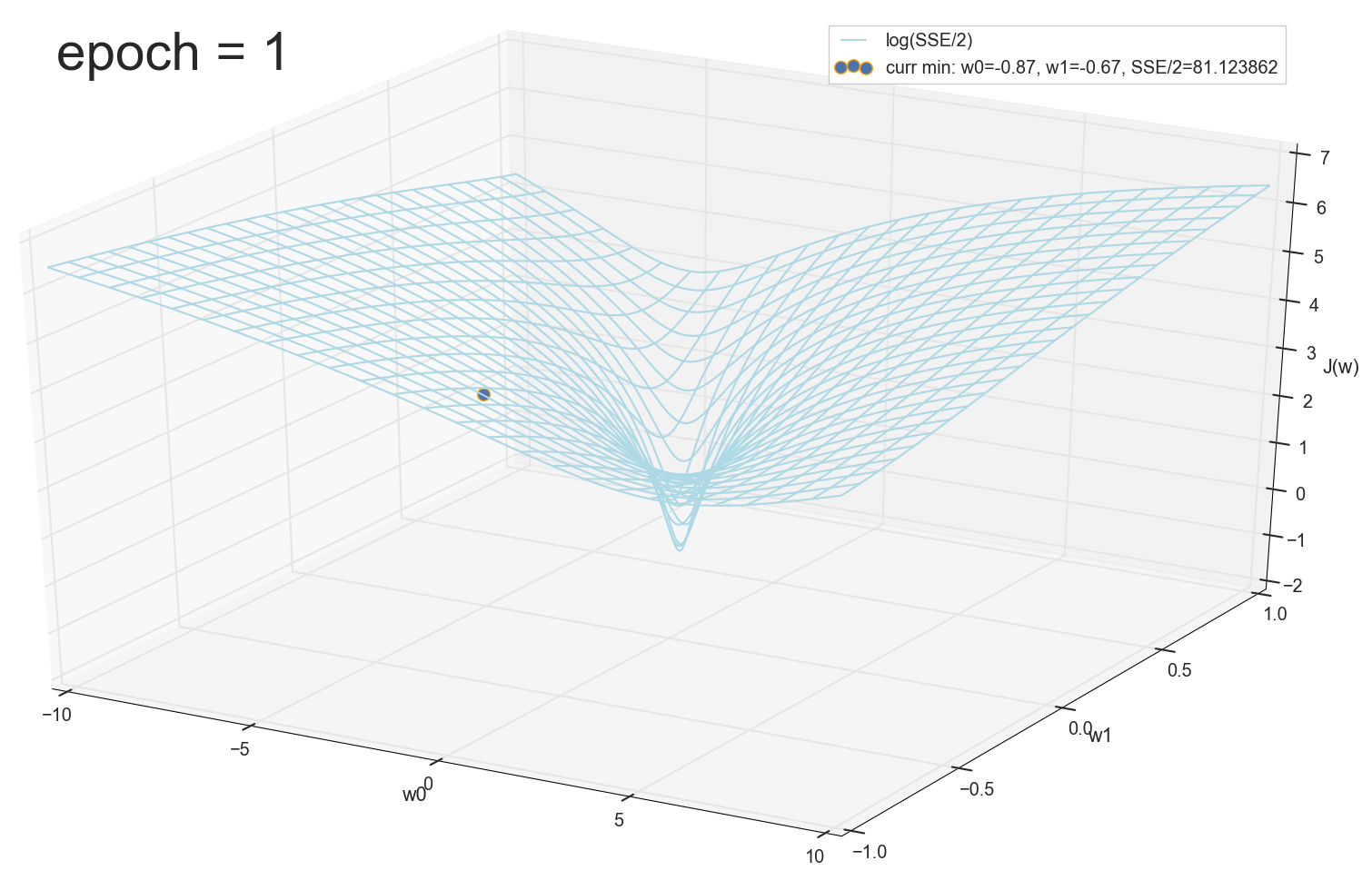
12 — , :

50 :

1767 — , :

, 62000 :

:
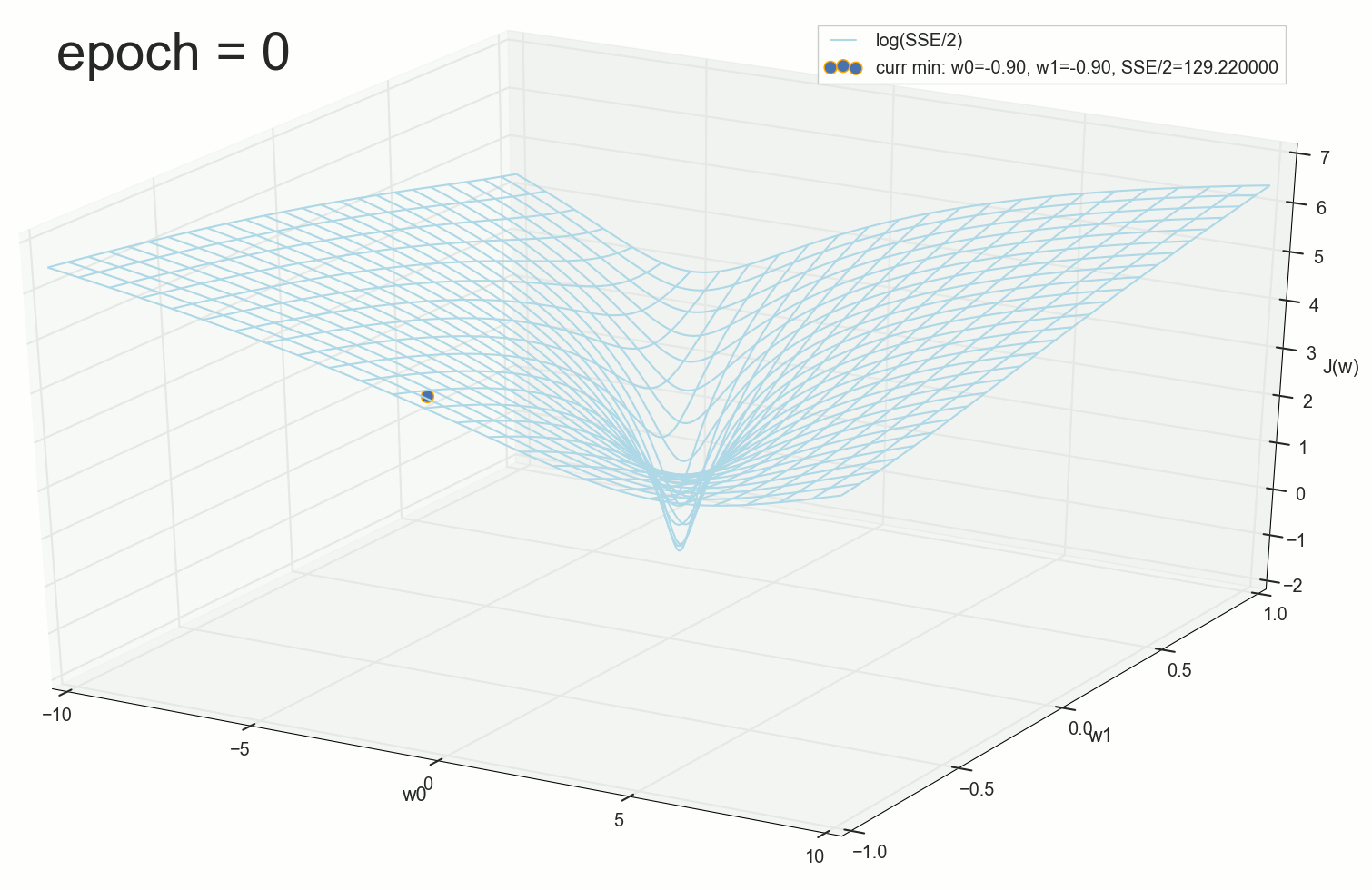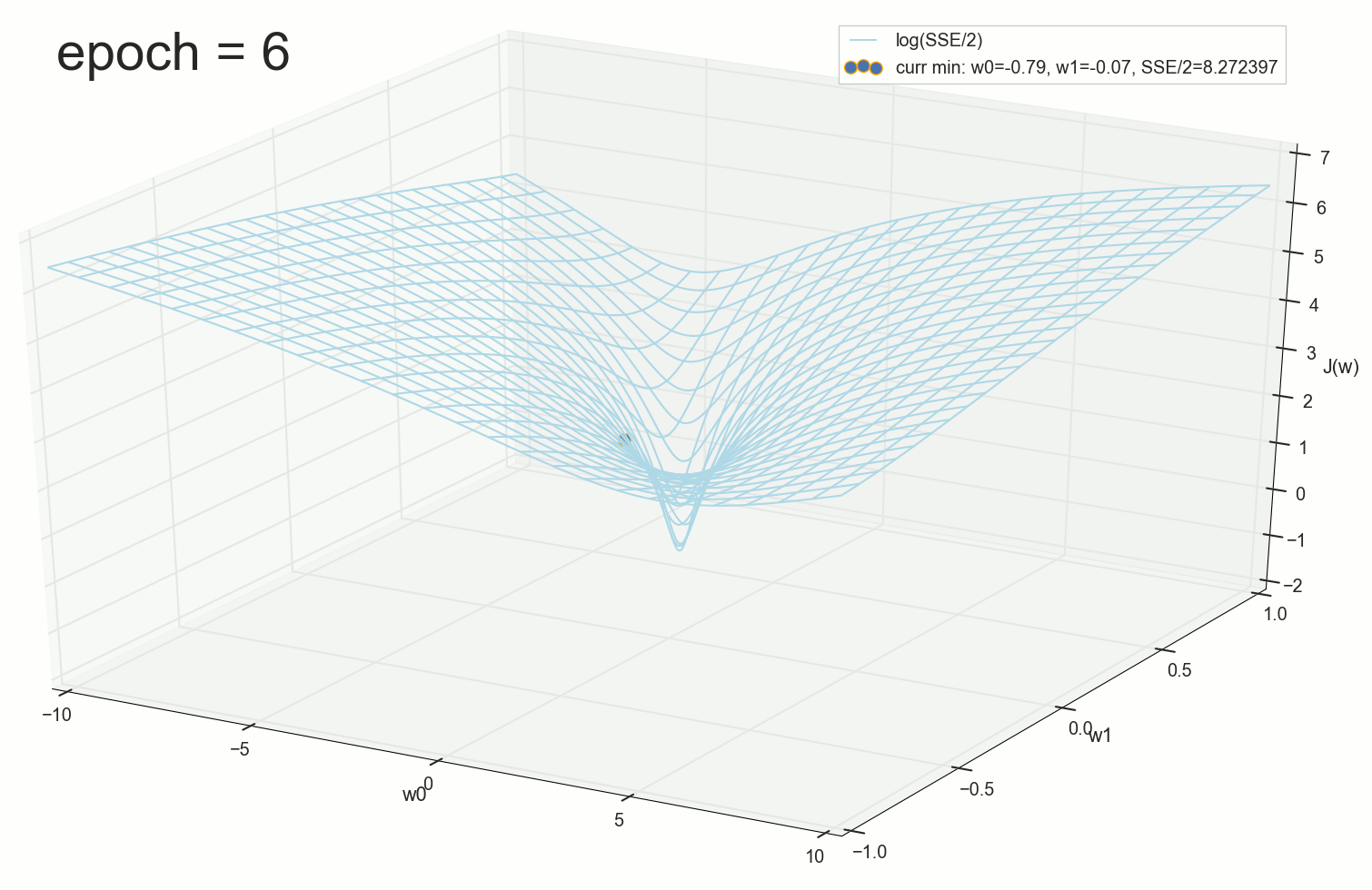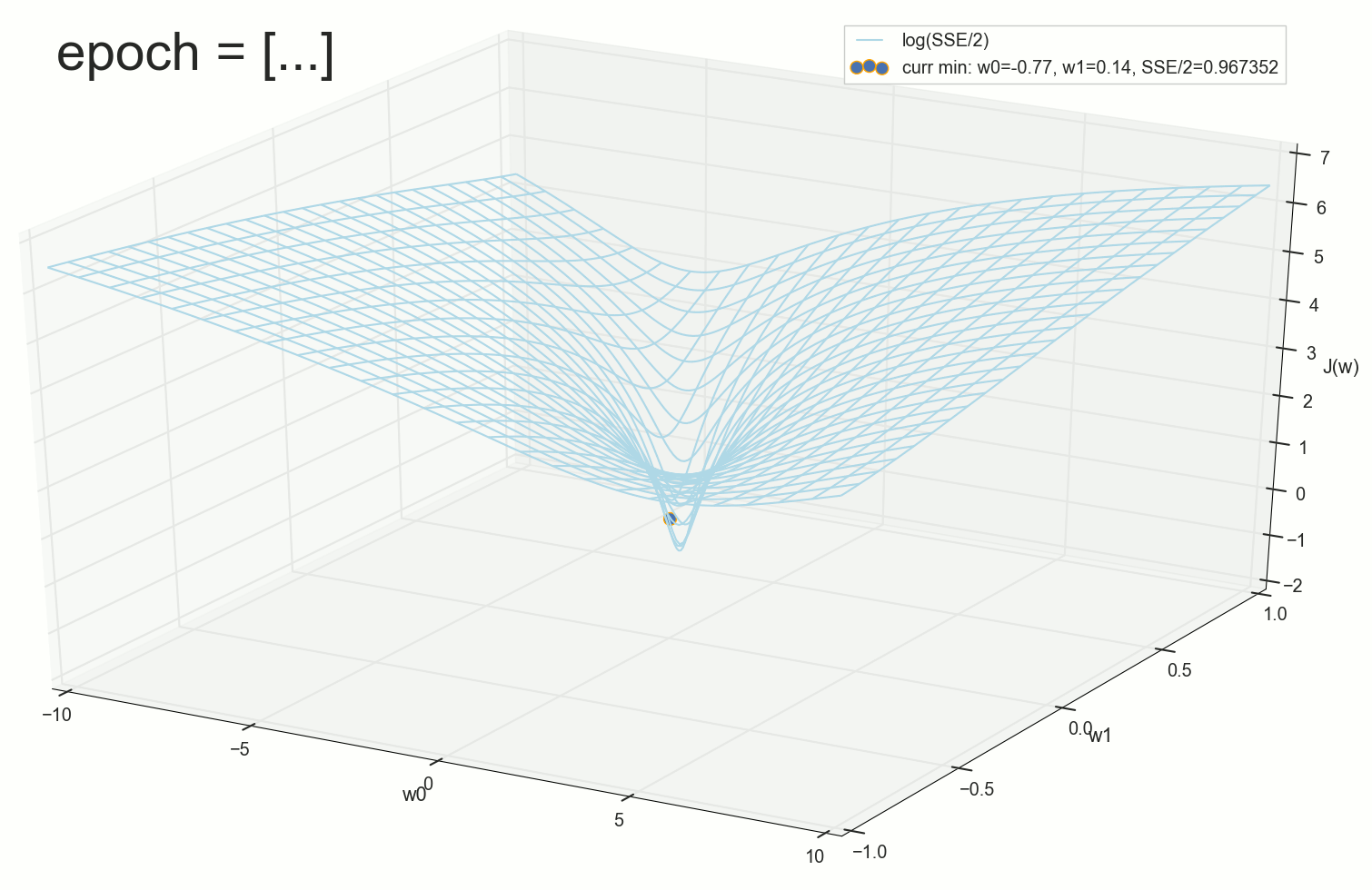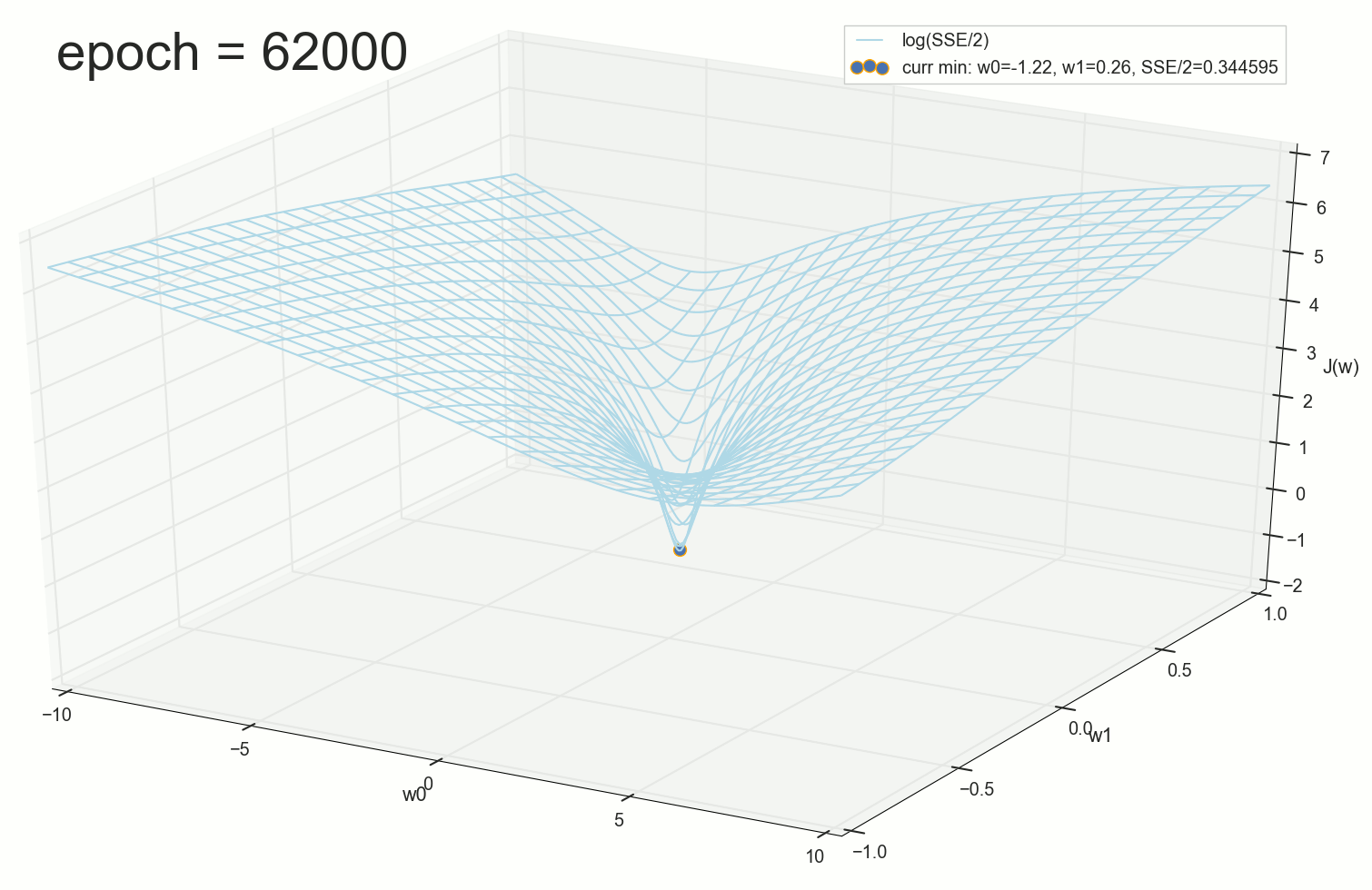
. , : , , . , , , , , , . , , - .
, , - , - : , , , , , — . , , , , , , , — . 怎么了
, . :
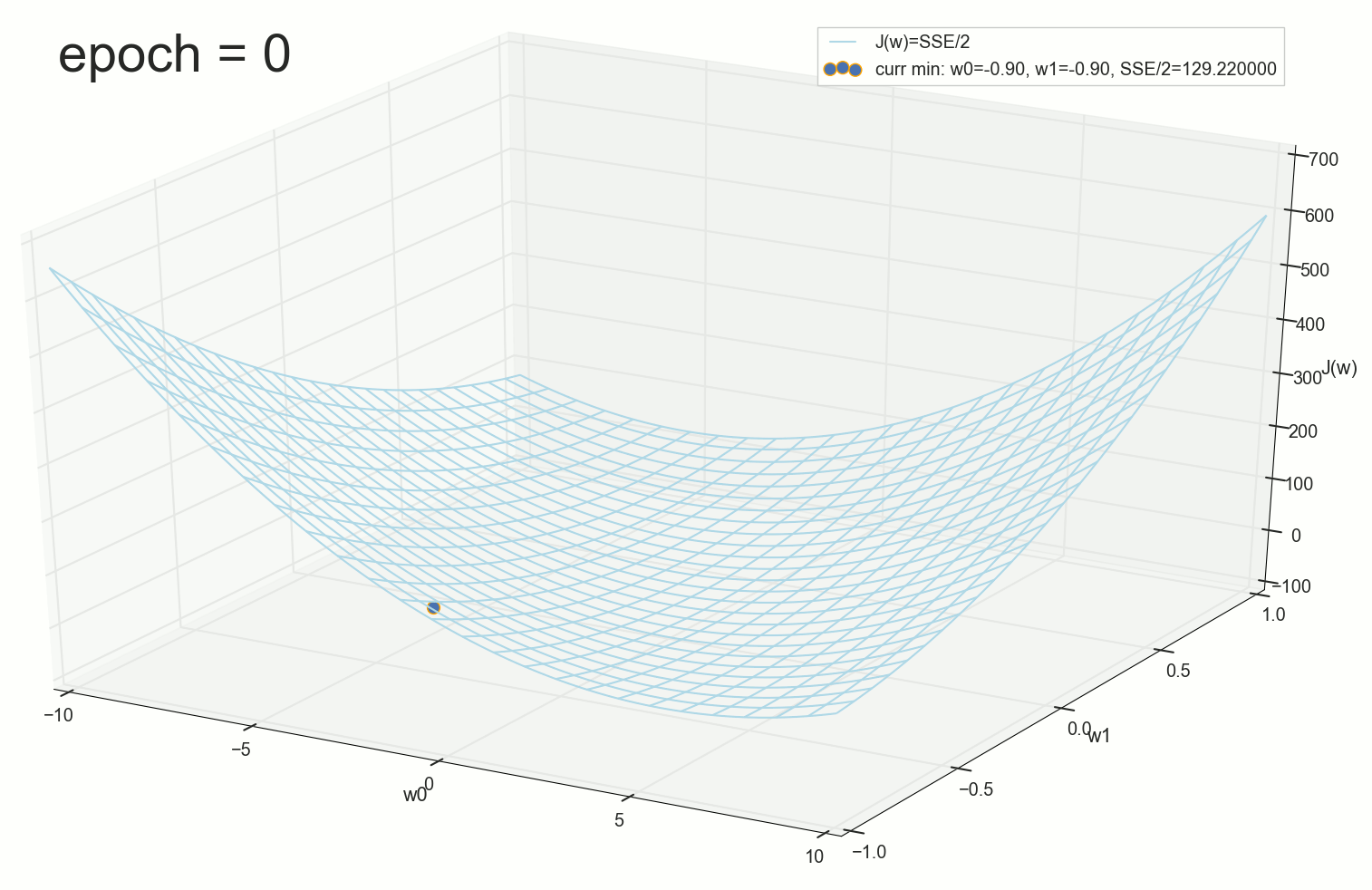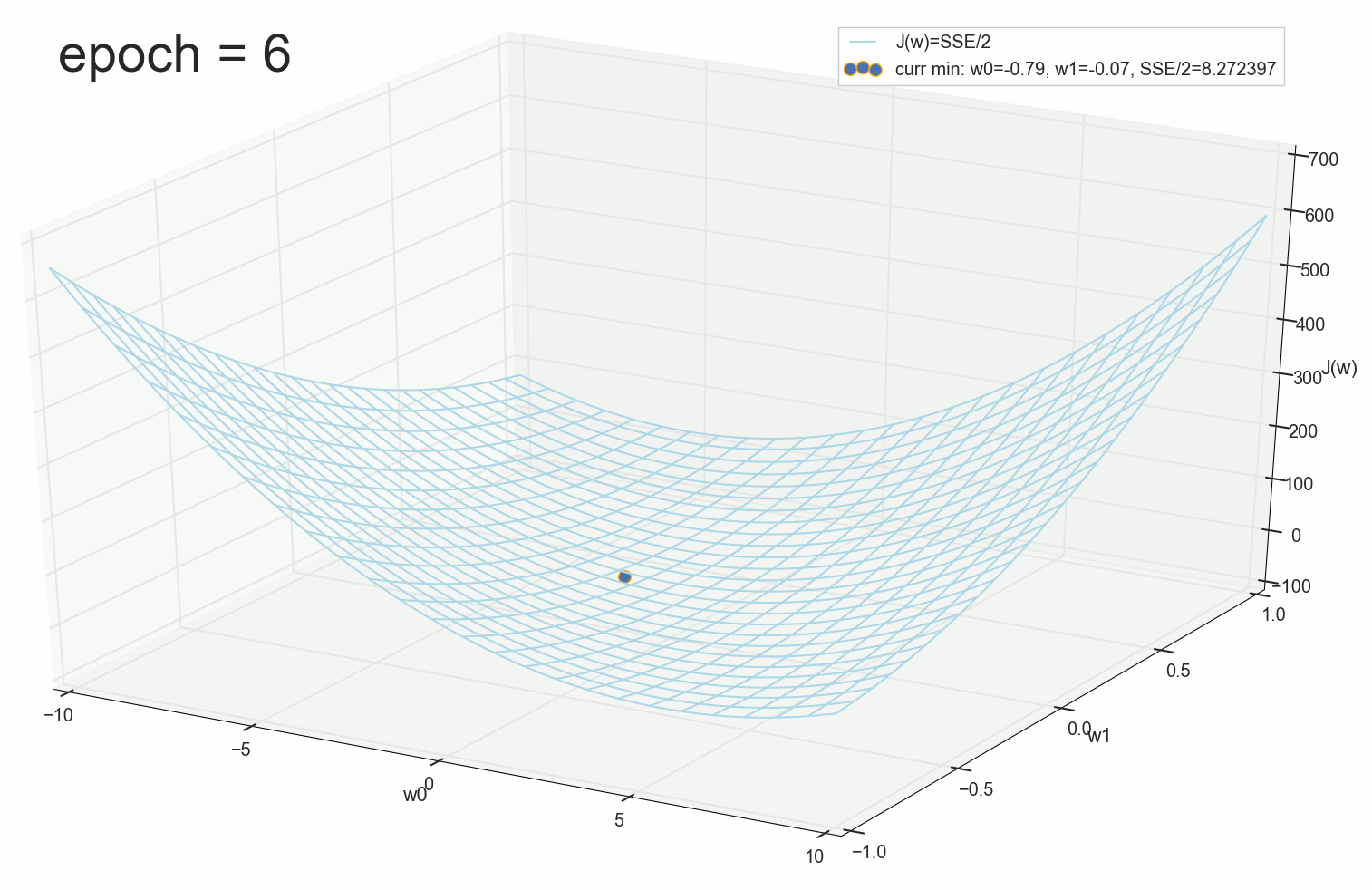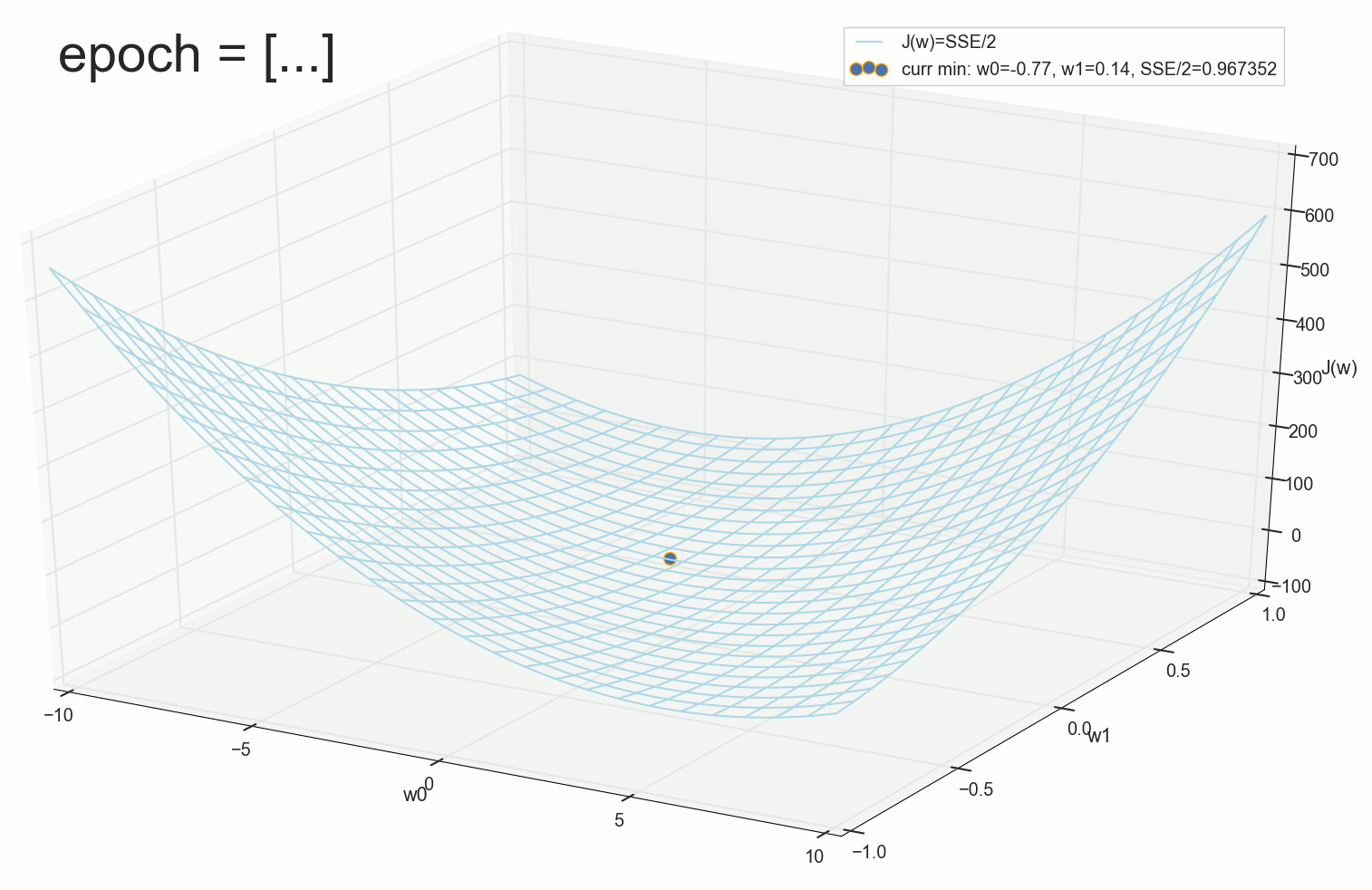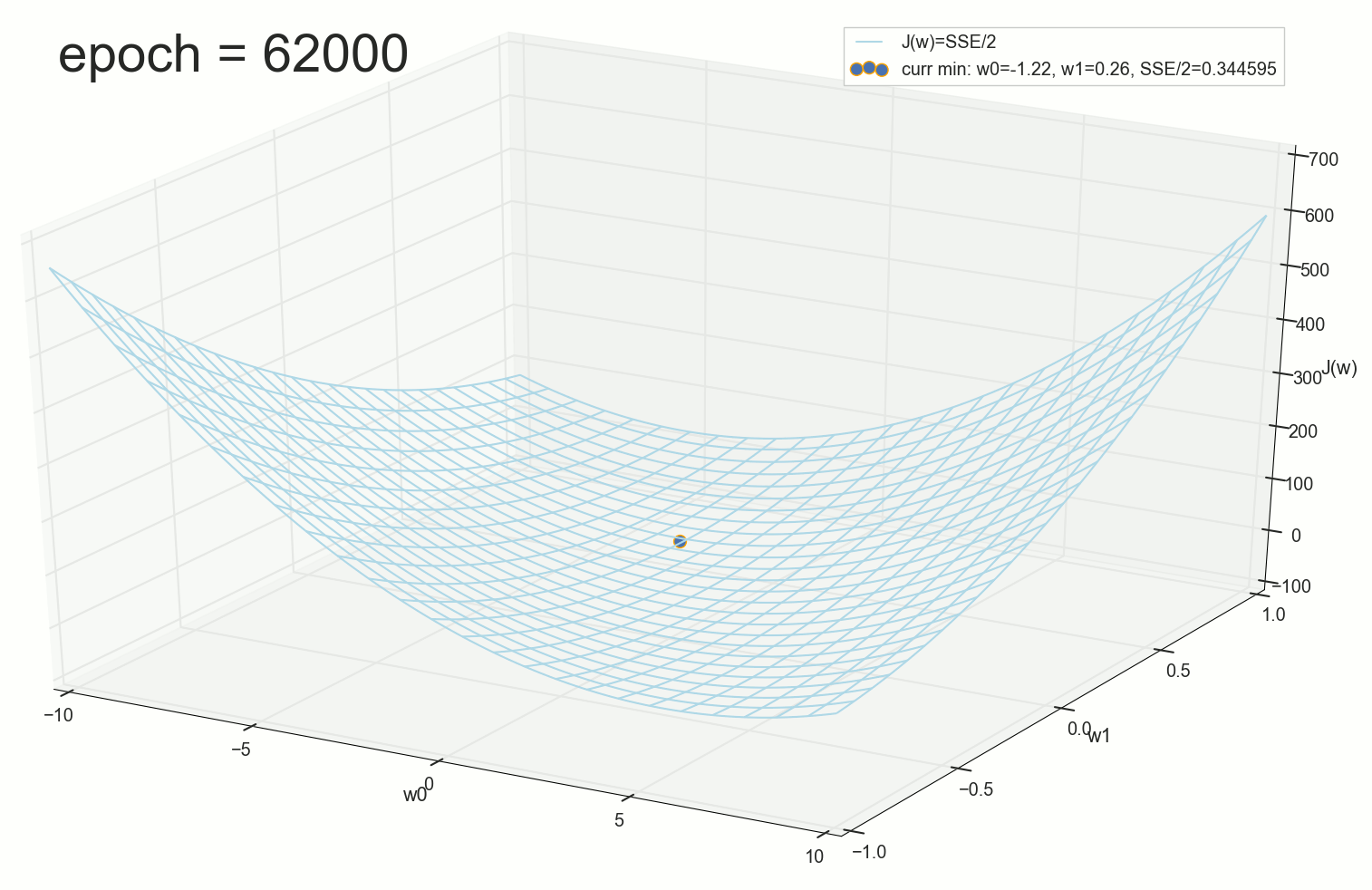
, , ( ). : , . , , .
. , .
. , , . , — .

— :

11- : , ; :

12- : , , :

50- : , 12-

1766: . J(w)=0.3456480221 — , , ( J(w)=0.3456478372 : 6- , , )

1767: J(w)=0.34564503 — , ( 6- , ). w0=−1.184831 , w1=0.258455 ( w0 2- : w0=−1.27 , w1=0.26 )

62000: J(w)=0.3445945 — , ( 2- ). :

:
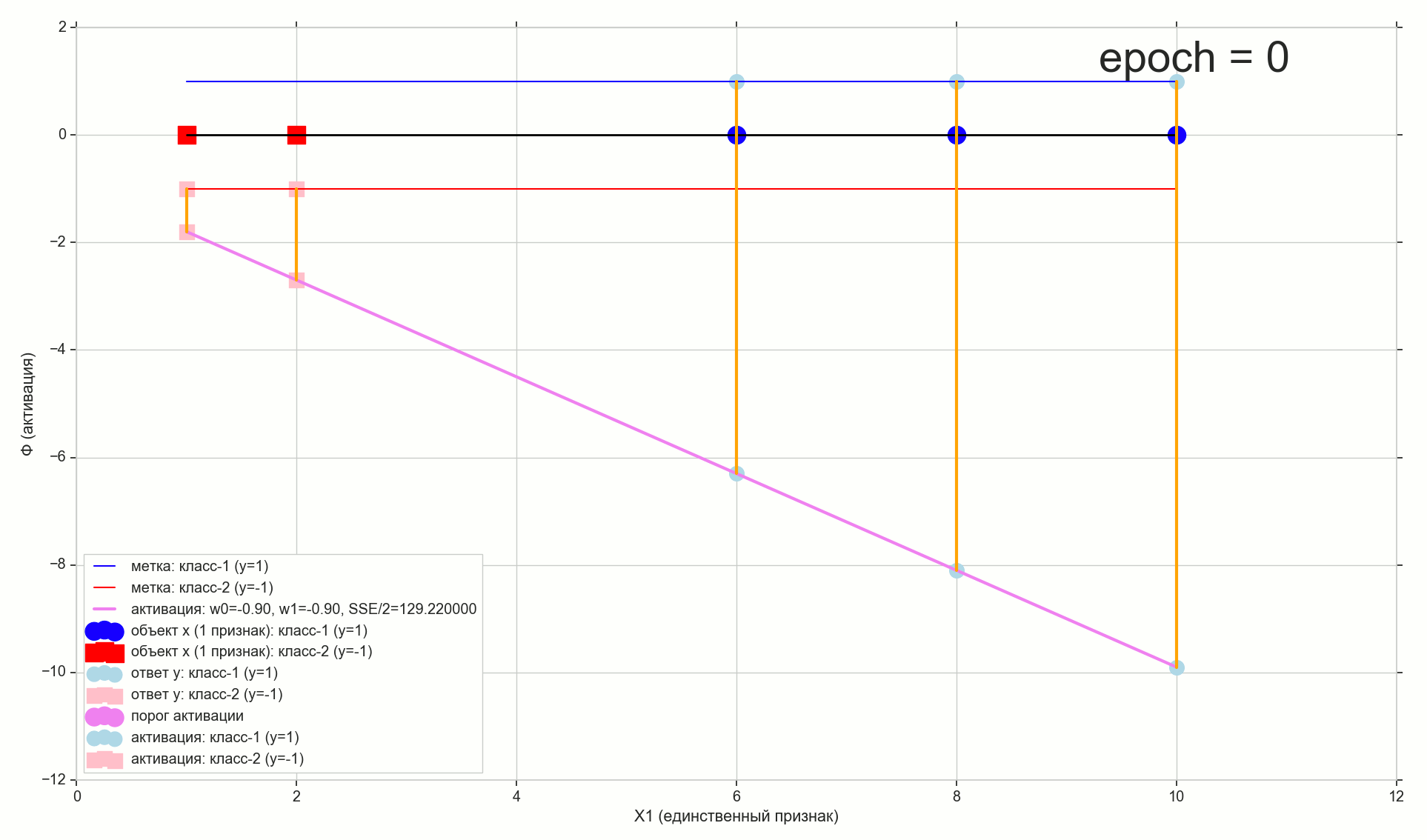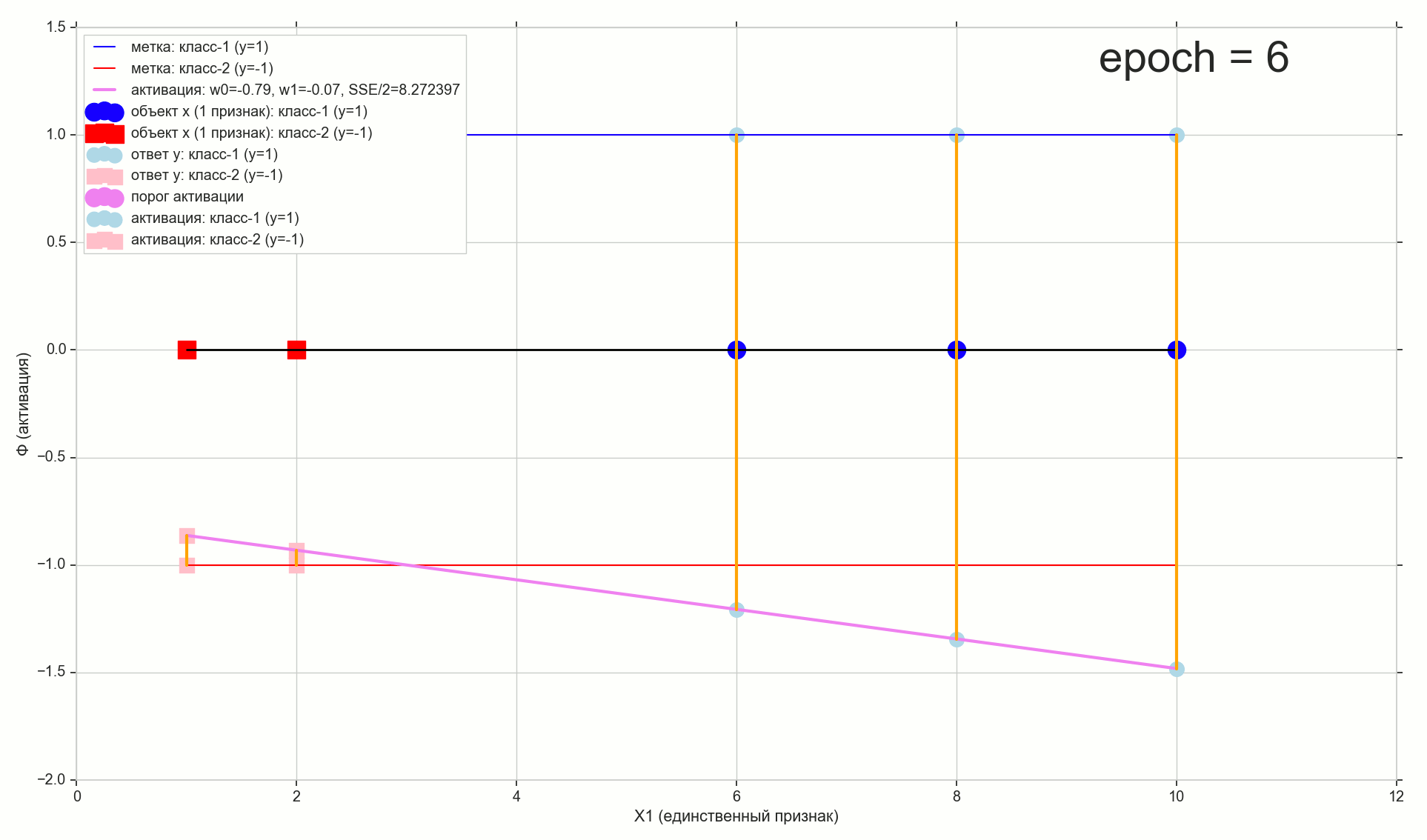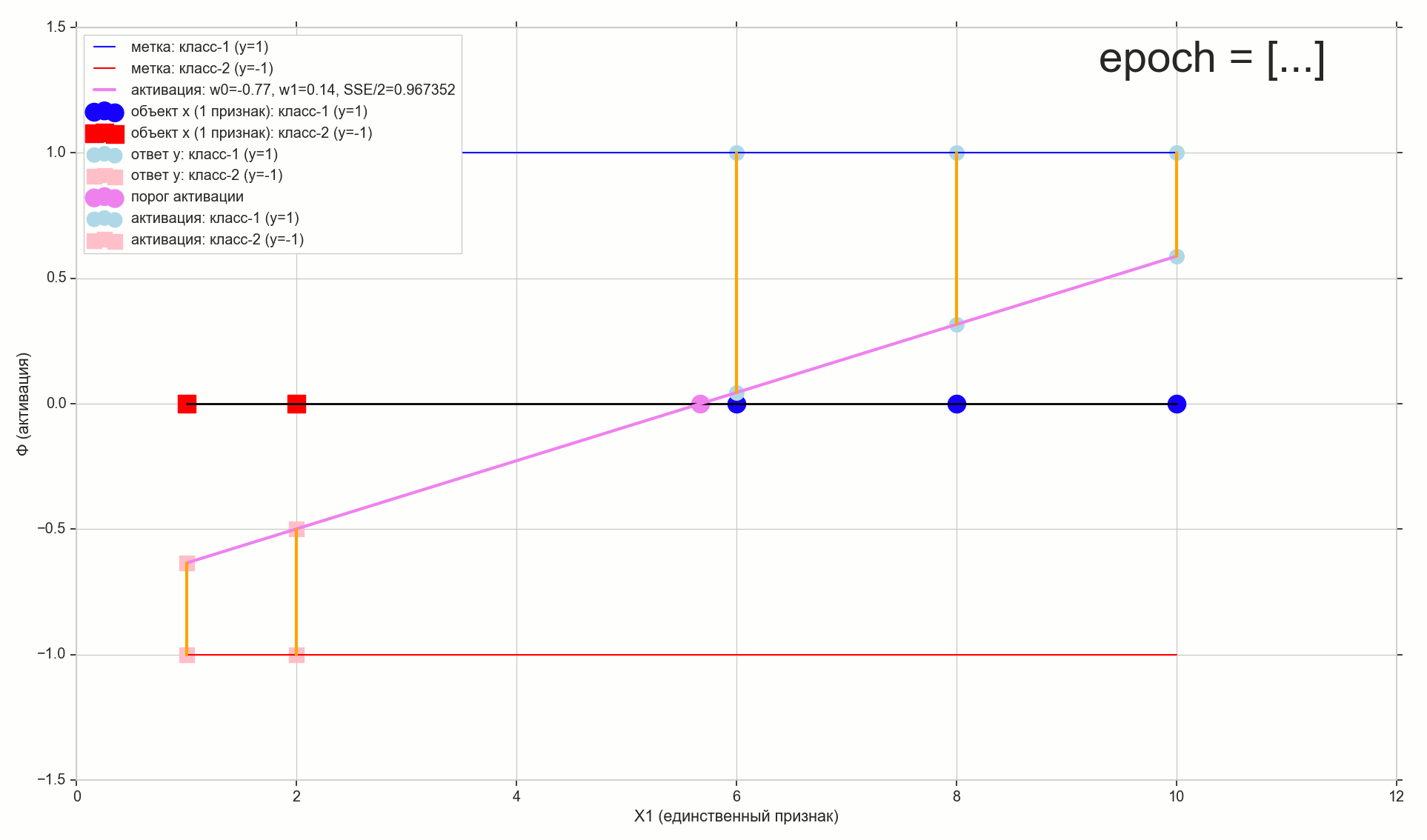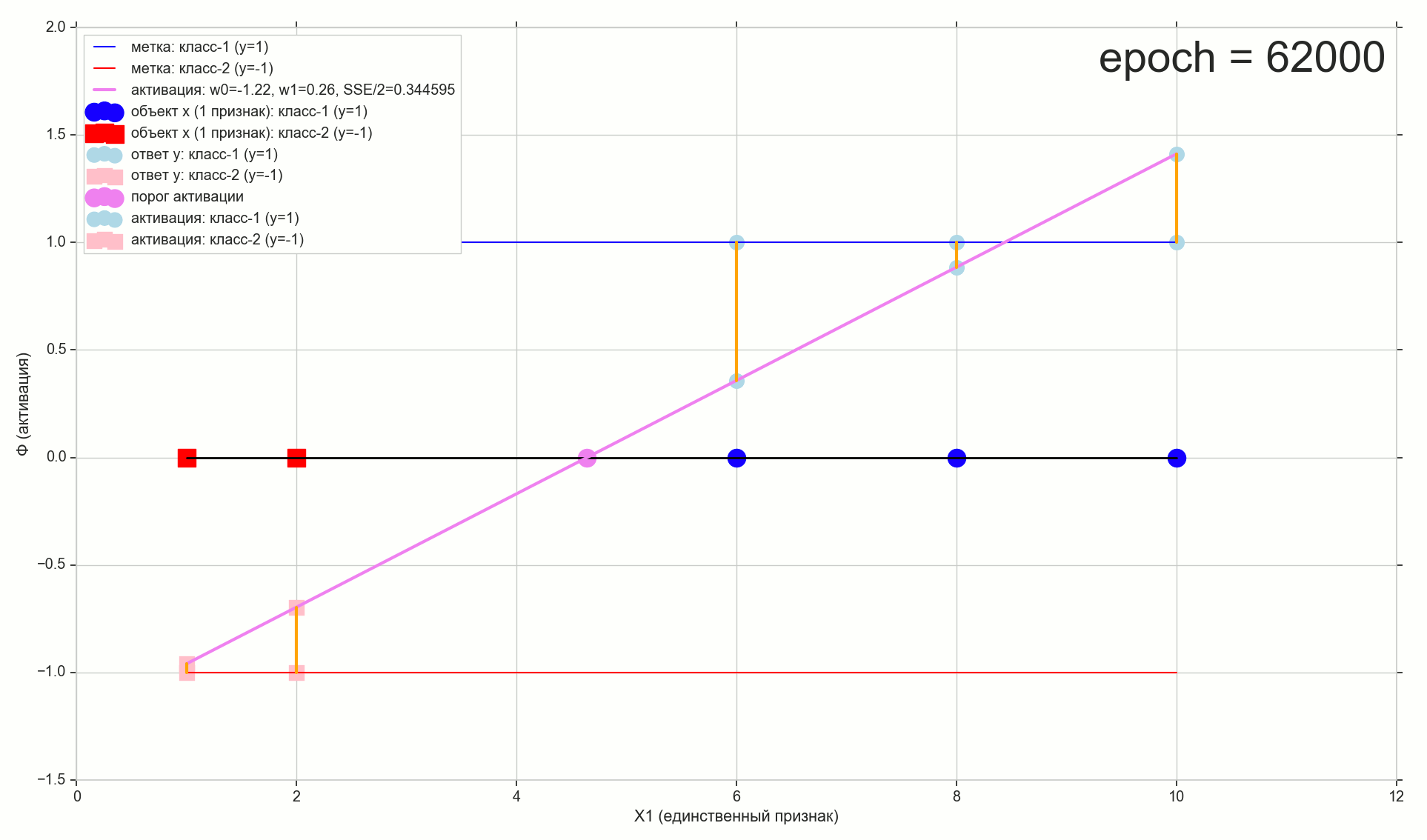
. , , , , .
- η=0.001 , 10-12- ( )
- , , , (1767)
- — 60
- —
— ( , 1767): w0=−1.184831 , w1=0.258455 。
.
t(1)=(t(1)1)=(1.4) ( , t(i) — ). , .. , , ˆy=−1 , .. .
SUM=w0+w1∗t(1)1=−1.18+0.26∗1.4=−0.816
Φ(SUM)=SUM=−0.816
Φ(SUM)=−0.816<0⟹ˆy=−1
, .
: t (2 ) = (t (2 ) 1)= (7 )
Φ(SUM)=SUM=−1.18+0.26∗7=0.64⩾0⟹ˆy=1
ˆy=1 , .. . .
, ( «» ) 12 . , !
(m=2)
, , , . . , , .
— ( ). 2- .
- x=(x1,x2) ( , , )
- y={−1,1} ( , )
plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1')

, .
Φ(x,w)=w0+w1x1+w2x2
, — , , 1- , 3-:

:

:

— :

() Φ(w)=0 (-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).
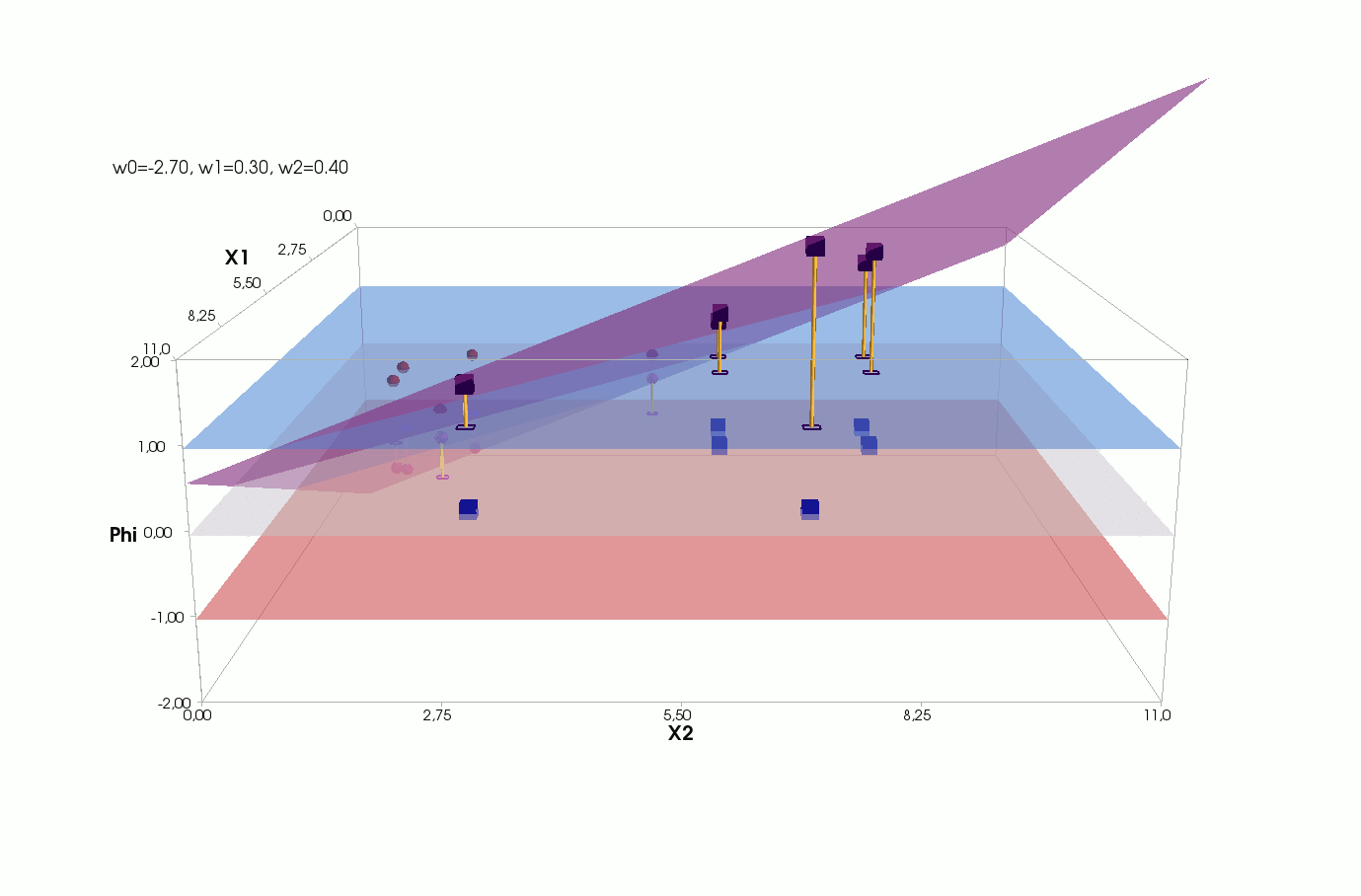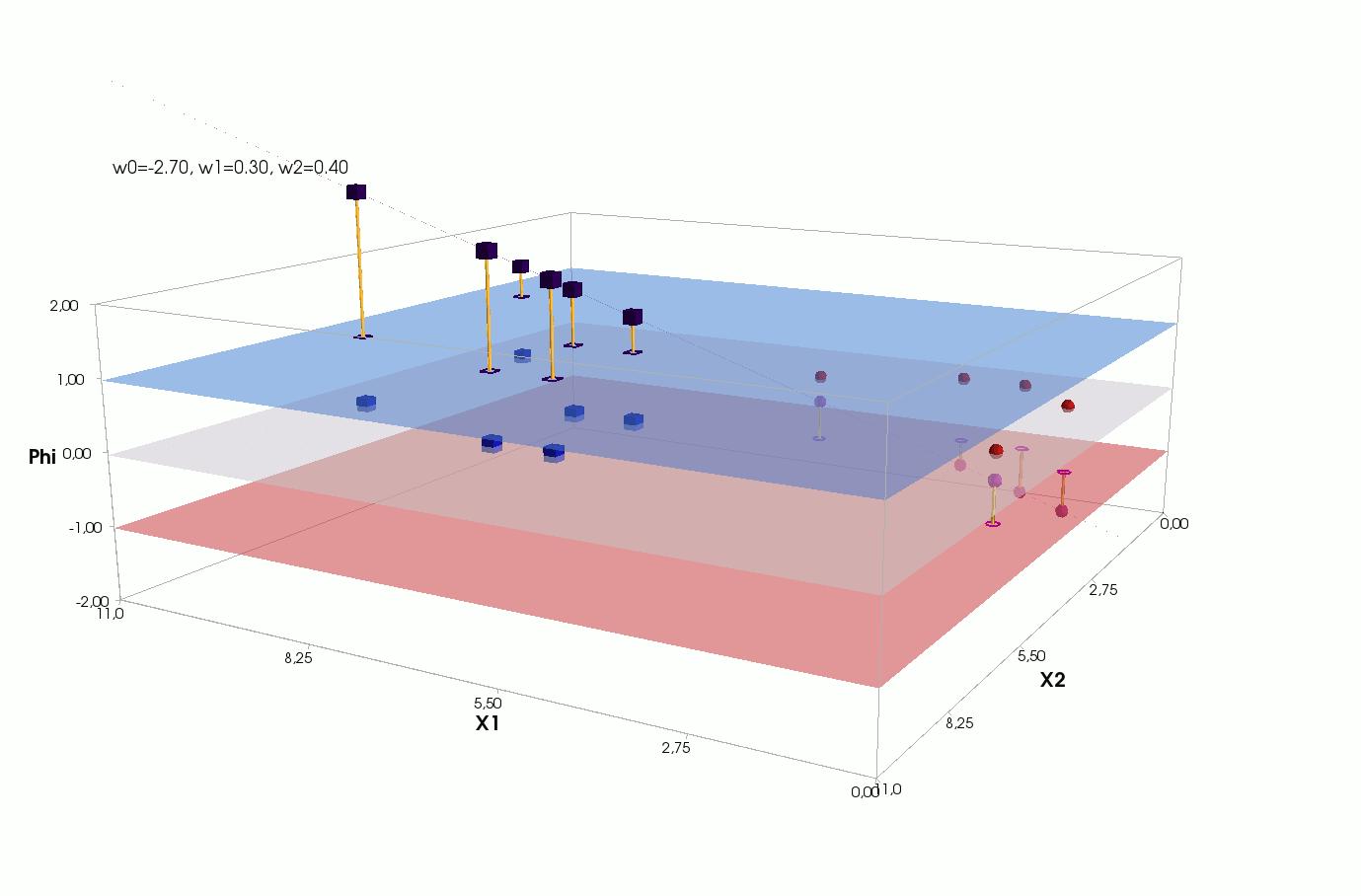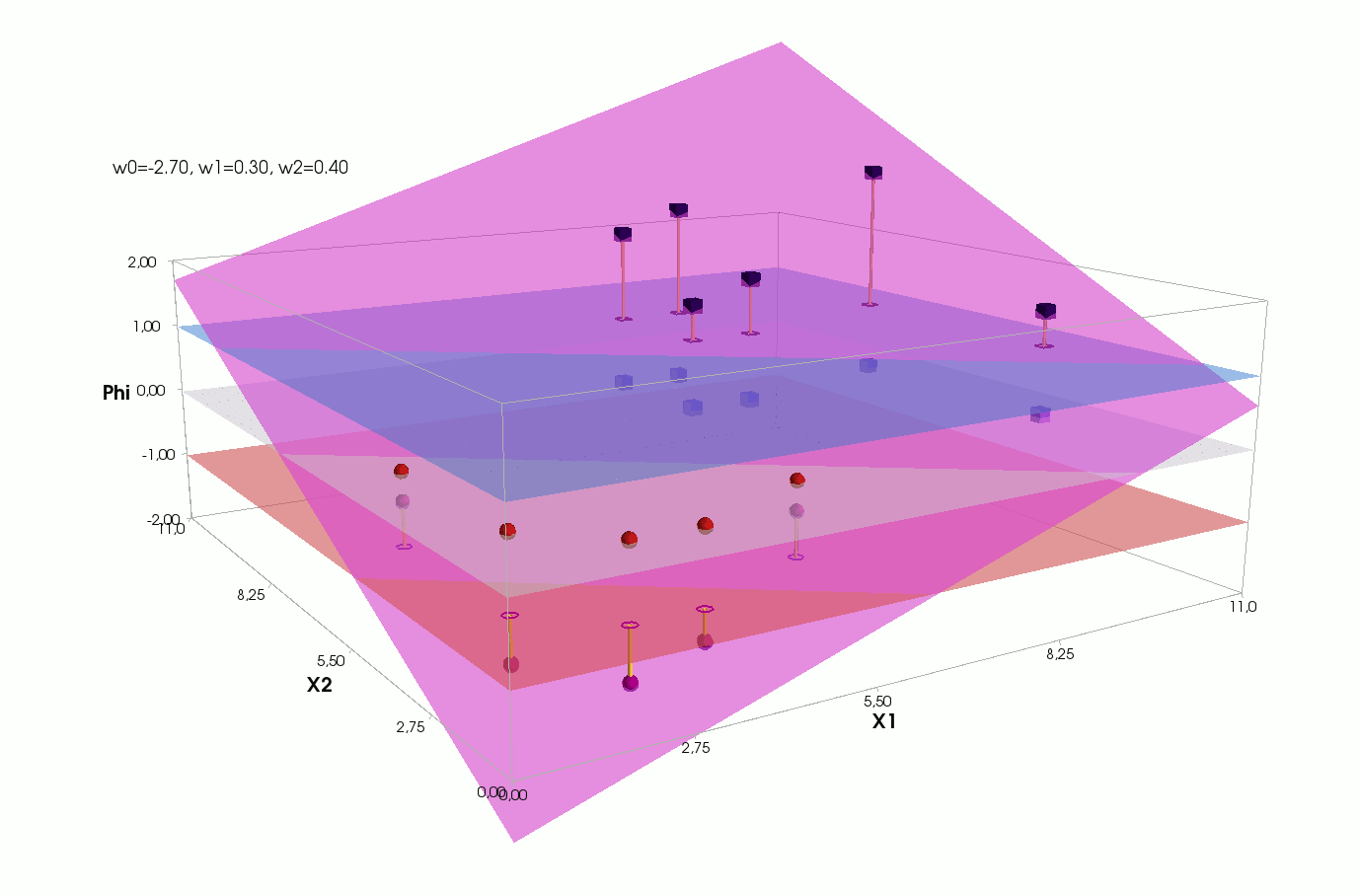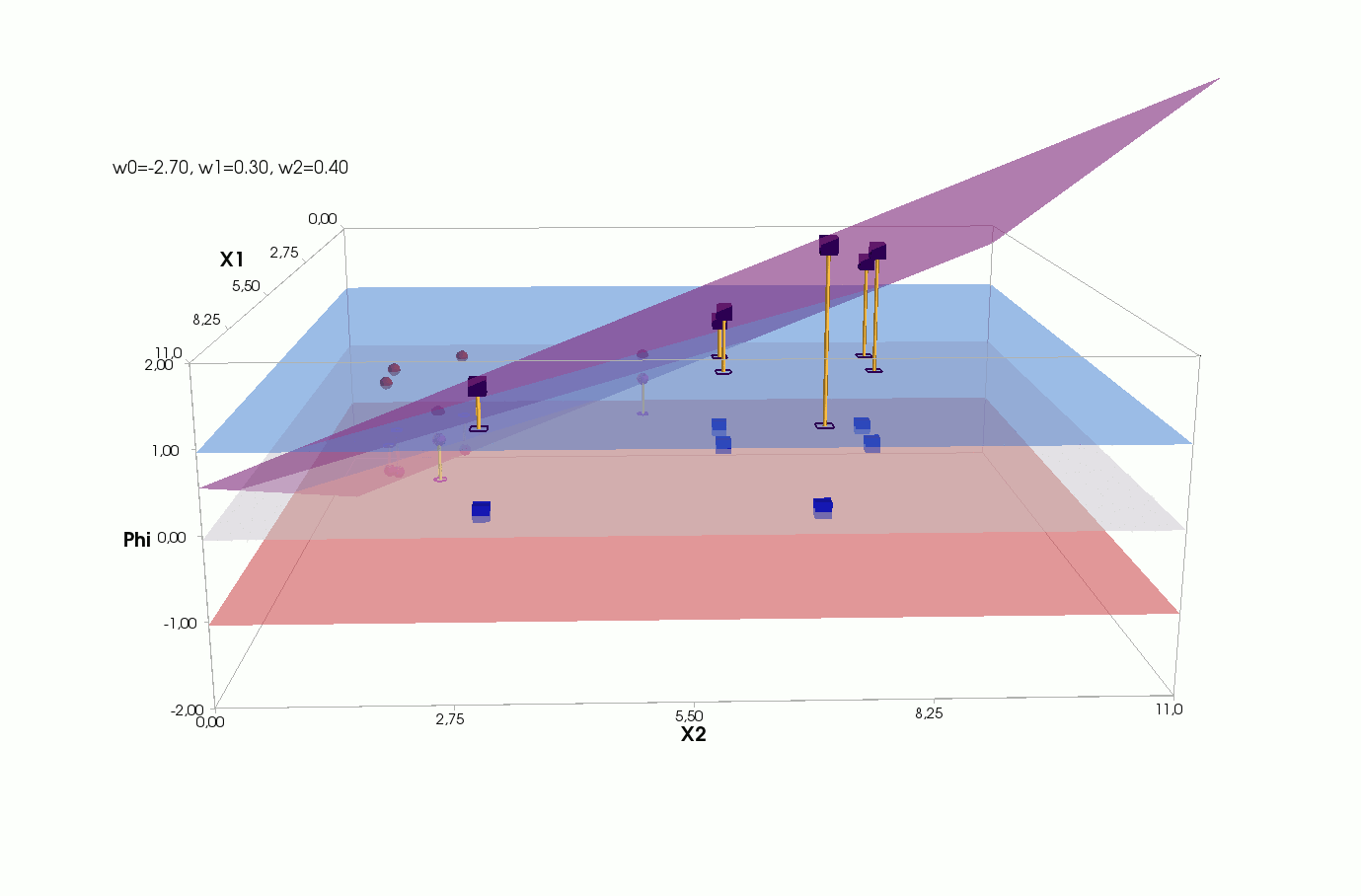
J(w)=12SSE=12n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))2
() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .
2- . , , 1- 2-.
∇J(w)=(∂J(w)∂w0,∂J(w)∂w1,∂J(w)∂w1),w=(w0,w1,w2)
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
∂J(w)∂w2=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
Δw2=−η∂J(w)∂w2=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
3- ( 3- ), η=0.001 , w0=−0.9 , w1=−0.9 , w2=−0.9 。
— , , :


:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , w0 。
代号
matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .
import numpy from mayavi import mlab
, Mayavi , . , , , .
Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :
env QT_API=pyqt python3 gradient-2d.py
— J(w)
def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum()
12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .
结论
ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .
«Python » ( scikit-learn) , - .
ADALINE .
-, — , : , , , .
-, () , , , ( , , y ) — , scikit-learn.
PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .