在前面的系列中,我们从几个不同的角度看了分数。 在本系列中,在
介绍和一些
理论基础之后 ,我们将尝试以方便的形式收集所有内容并从可用信息中受益。
搜索简单
讨论了残差表的属性后,我们可以尝试将有关它的知识应用于收益。 因此,世界上许多人发现搜索大素数很有用。 甚至有些组织也准备向发现大量素数的人提供大量资金。 但是量子计算的话题在世界上也很流行。 怎么了 因为它有望破解一个著名的密码系统。 可以说,这就是量子计算的广告口号,它可以说服任何决策管理者为这一有趣的课程分配资金。 因此,我们还将讨论这个主题。
首先,我们将向您展示如何查找素数。 这里的主要问题是数量。 对于大数,根本没有算法可以让您快速检查素数在我们前面还是在复数前面。 因此,今天的最大停机时间少于2500万小数位。 这只有10兆字节,在这样的阵列上,现代处理器显示毫秒级的处理时间,但是要检查素数是否在我们的阵列中,现代处理器将用风扇消耗电力和嗡嗡声长达数十年。 即,从技术上讲,处理器的大小并不好,但是已知算法中如此大量的运算数量实在是很大。 为什么会这样呢?
例如,对于简单性测试,使用了除法器的枚举。 但是,您需要迭代多少个除数才能达到十兆字节的长度? 答案是,即使在整个宇宙中带有电子的原子也仅足以满足该值的一小部分。 也就是说,我们需要大量的宇宙,只是要将所有这些除数放置在那里。 太多了吗 因此,在有限的范围内应用了十兆数字除数的枚举(是的,宇宙让我们失望了……),但是幸运的是还有其他算法。 我们可以区分不使用除法器枚举的算法,同时保证可以给出答案-在我们面前很简单,也可以很简单。 但是这些都是非常慢的算法。 也就是说,它们当然能够以这种方式研磨一百或两百个比特,但是十兆字节对他们来说就是一次死亡。 因此,您必须摆脱棘手的方法。
但是所有技巧的问题在于它们还没有提出完整的可除性理论。 毕竟,如果它是完整的,我们将很快找到答案-是否是最佳答案。 更准确地说,一种理论会很快为我们提供一种测试算法,该算法不会让我们等到宇宙热死。 这就是为什么他们会给那些尽快提出算法的人加分的原因,最重要的是,他们会为在各种场合提供算法的整个理论提供奖金。
同时,我们可以使用特定的Luc-Lemer检验,该检验使用非常特定的Mersenne数与特定序列的连接,而不是我们最近观察到的除法除法余数,而是某些非理性数的和。 也就是说,简单性测试是从侧面进行的,虽然不是很明显,但是这里有些可以进行更复杂的比较。 但是,为什么无理数的度数比数论的所有其他成就更接近简单性检验? 显然是因为数学不知道简单的解决方案。 结果,从不是最接近整数计算的区域中使用了一种虽然不是很明显但仍在起作用的方法,大致来说,从笛卡尔坐标到极坐标的过渡如何帮助使用很难在笛卡尔坐标中实现的其他方法。
除Luc-Lemer检验外,还进行概率检验。 他们帮助清除有保证的化合物编号。 因此,最常用的概率测试之一是基于费马公式的测试,这是我们最近谈到的。 他如何工作? 很简单-还记得余数表右边的单位栏吗? 这是数字简单性的保证标志。 为了解释使用费马公式进行的验证,数学家使用了很少有人能理解的特定术语,因此,我们不会深入这些数学丛林,而是会用手指或从残差表中解释所有内容。 要了解最后一列中的余数,您需要除以一列并在其中包含1的位置达到余数,或者使用允许您通过位置编号和数字系统的基数获取余数的公式来计算此余数。 数字十兆字节长的第一个选项将需要几乎无限的时间,因为表的宽度为N-1,这意味着对于一百万个数量级的表,表将至少具有一百万列。 十亿,十亿。 一万亿,一万亿 但是,万亿,只有12位小数。 我们对数量在2500万以内的字符感兴趣。 即使采用分割列的方法计算出一万亿个残基,我们也必须计算不到半小时,而这仅是12位小数。 总计! 则为2500万。 您认为您有足够的时间以这种方式等待结果吗? 因此,最好使用公式立即计算所需的值。 而且只有费马公式与计算表中最后位置余数的公式相对应。 此外,如果周期短于表格的宽度,则数学尚不知道如何计算该周期,这意味着无论如何我们都需要选择最后一列。 测试中的数学家只是检查最后一列中的余数是否等于他们选择的数字系统的一数(尽管数学家不使用数字系统的概念,因为他们只有幂的基础)。 如果余数不等于1,则保证该数字为复合数。 正如我们在数字21的表格示例中看到的那样,正是在许多行的末尾没有单位将其与质数表区分开。 但是有一个问题。 在某些行上,可能仍然存在单位,我们也可以通过21的表格示例进行验证。这就是为什么数学家基于费马公式概率来称呼检验的原因。 也就是说,如果Fermat测试发现余数等于1,则他们不知道该数字是否为质数,因为这样的错误单位在数字21的表中,甚至在10兆字节的数字中,在许多其他表中也是如此。 因此,您需要检查一行中的所有行(这很长),因为如前所述,十兆字节数字的行远远超过我们知道的宇宙中的所有内容,或者只是说-这个数字很可能是质数。 这是数学家选择的最后一种方法。 幸运的是,几乎没有几行以大多数复合数字结尾。 的确,还有所谓的Carmichael数,其中除该数的除数的倍数以外的所有行都以1结尾。 因此,在Carmichael数上,通过费马公式进行的概率检验实际上可以保证是错误的,因为要消除该错误,您需要将数除数为整数,并且十兆的除数只能有两个,并且它们的值可能非常大,因此得到的可能性很大。正是在这样的一条直线上,通过随机选择数字系统的基数,它实际上为零。 但另一方面,Carmichael数相对较小,这使我们有希望进行概率检验。 仅当搜索素数时,才排除了可能性的希望。 这就是为什么在借助概率检验选择简单候选人之后,仍然应用了Luc-Lemer检验。
添加一些关于Carmichael的数字。 他们不仅以模仿简单的东西而著称。 因此,网络上有一个网站,您可以在其中学习不同
的数字序列 。 如果在搜索字段中输入数字561(最小的Carmichael编号),您会发现它参与了大量的序列。 这是在说什么 显然,我们这个世界上很常见的一些相似数量的未知结构特性。 非常有趣的事实。
回到简单测试。 尽管通过概率测试获得了很好的滤波系数,但是人类花费了数年的时间才能找到下一个最大素数。 怎么了 因为测试执行时间对数量大小的依赖性是二次的。 也就是说,对于较小的数字,一切都会爆炸,并且没有问题,但是,当数字增加一百万次时,计算时间将增加一万亿次。 因此,在单个处理器内核上,我们将考虑进行Luc-Lemer测试数十年。 但是,即使通过费马公式进行测试,我们也将考虑相同的条件。 也就是说,在两种方法中,计算数量都达到了人工能力的极限。 您必须为此做些事,不是吗?
多年以来,这种浪费大量的空气加热计算浪费的替代方案是什么? 非常简单-您需要根据数字的性质,其在特定类中的成员身份来预测简单性。 因此,正是由于Mersenne数属于特定类别,它们才成为已证明质数的已实现大小的领导者。 Luke-Lemer测试专门针对此类特定课程。 由于缺乏甚至十卢比数字的Luc-Lemer测试之类的昂贵测试,其他类的数量也滞后(尽管有些测试是改编的)。 因此,我们需要对数字进行分类,以使我们能够找到简单的简单性测试,所以天堂原谅我这种双关语。
如何创建这样的分类? 这也不是那么困难-您需要研究不同的数字并找出它们之间的共同特征。 通常,这正是数学家正在尝试做的,但是到目前为止,还没有出现一朵石花。 因此,我们将尽力帮助他们。
前面描述的基于残差表的数字分析方法实质上探索了形式为1000 ... 000的数字可除性。 也就是说,右边的零始终分配给该单位,从而将其乘以剩余表中存在的每个数字系统。 分析的结果是,我们发现不同的数字以不同的方式划分形式为1000 ... 000。 因此素数通常不能将一除以零。 但是成分,甚至是例如二和/或五的成分,都被完全分割了。 下表是数字8的表格:

如您所见,在非零残差的某些项输入之后,在2的倍数行中,仅保留一个零。 这就是所有与零的单位除数类有关的数字的样子,而零的存在告诉我们我们将在哪个数字系统中成功。 但这是问题所在-从查找质数的角度来看,零的单位对我们来说根本没有意义,因为可以保证将其除以数字系统的基数,这使我们将所有这些零归一。 因此,您需要研究其他类别数字的除法。 这合乎逻辑吗? 这正是我们将要做的。
我们可以尝试除数理论吗?
早些时候,我们熟悉了除法运算中余数表的规则,这是我们相对熟悉的。 这些模式原来很有趣,但是它们仍然存在相同的问题-它们没有为我们提供检查简单性的快速算法。 对于这样的测试,就像根据费马公式进行的测试一样,我们将不得不大幅度提高数字,然后找到将结果除以所研究数字的余数。 或者只是简单地使用“角点”方法遍历所有残骸(当然,是在宇宙热死之前)。 这是数据-求幂数并找到余数的操作在一个核心上需要15分钟以获取订单数
。 随着数字大小增加1000倍,我们得到至少1,000,000倍的平方增长(加上对数,但这不是那么多),但实际上是-数百万倍。 假设结果是,我们一次测试可以花费一百万小时。 这大约是40,000天或明显超过一百年。 如果我们尽早优化测试的执行,并考虑到处理器体系结构的所有功能来执行测试,那么也许不是一百年,而是10年。10核-1年。 对于1000个内核-4天。 但这只是一个概率检验,因为有化装舞会作为简单的复合数。 因此,您仍然需要仔细检查。 但更重要的是,候选人人数达数百万。 在所有可能的过滤之后,还会有很多过滤。 因此,世界仍然混乱着十兆字节的数字。
但是我们有一个工具。 其余表也适用于其他类型的数字。 例如,采用梅森数字。 以二进制形式,它只是一个单位序列。 是什么使我们无法探索单位序列而不是零序列? 是的,没有什么可以阻止的。 事实证明,对于这样的序列,我们的方法运行得很好,并且其中保留了许多以前确定的模式。 这是数字7的结果:

我们可以看到,所有数字系统中的质数7(除7的倍数以外)都是梅森数的除数。 也就是说,几乎每一行中都有一个零,告诉我们形式111 ... 111(在二进制系统中)的数字除以7。因此,当使用二进制数字系统时,我们看到数字7将所有梅森数字,长度这是3的倍数。在没有残差表的情况下,结果很明显-二进制形式的数字7由三个单位(111)组成,因此它将除以三个单位的二进制数。 如果有更多的单位,则该划分如下所示:
111111 | 111 ------ 111 1001 111 111 111
也就是说,我们只将7(二进制形式)放在股息下。 以及七个将适合多少次-这么多的三倍单位可分。 如果其中的单位数不是3的倍数,则该数字不能被7整除。但这仅在我们研究具有相同结构的数字(如示例中的7和63)时才是显而易见的。 如果数字的结构更加复杂,则残差表将对我们有所帮助。 因此,对于所有简单的结果,我们都得到了相似的结果,但是除法时间略长。 下面是数字11的示例(数字已经为十进制):
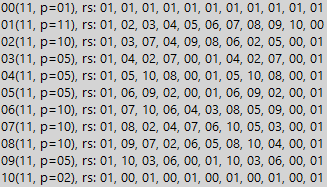
我们看到,在二进制系统中,数字11到零的距离(除数周期)是10。也就是说,任何包含10k单位(其中k是大于零的整数)的梅森数字都必须被11整除。可以很容易地证明其余的简单当然,数字的行为完全相同,只是周期的大小不同。 但是对于大院,情况再一次不那么和谐。 下面我们看到数字8的示例:

显然,8不能以二进制形式对梅森数进行除法。 请在三进制中显示-但梅森数只能由二进制形式的单位组成。 其他复合数字的情况与此类似-它们以不同的方式提供了所有内容。 素数的细长对称图像不会重复出现。 但是对我们而言,简单的正是最重要的,因为如果将数字除以质数,那么将其也除以包括该简单数的复合物就绝对没有问题。 但是,如果不将数字分为一个简单的数,则不可能将具有这样一个简单的数的复合数划分。 因此,我们应该只对素数感兴趣。
现在让我们总结一下。 我们知道Mersenne数被分为质数,并且为了可除性,Mersenne数需要一定数量的单位,该单位是所研究数字的除数周期的倍数。 但我们也知道,梅森素数的候选对象仅是单位数也是素数的那些。 即,除了单位和其本身之外,该金额不划分为其他任何内容。 因此得出结论-我们需要这样一个素数,其除数周期等于Mersenne数的长度。 如果在一定长度的Mersenne数中找不到合适的除数,那么我们前面有一个质数为Mersenne的数。 看起来很简单。
但是,进一步的困难开始了。 如何找到一个周期与梅森数字长度一致的数字? 要回答这个问题,您需要解决一个微不足道的任务-通过简单的方法找到一种方法来找出任意质数的周期。 目前,我们只能使用大角度公式在特定位置共享拐角或戳戳。 但是,如果我们可以不用长时间进行计算就可以计算出周期,那么我们将很快找到合适的除数,或者我们可以确保自然界中没有除数。 在研究形式为1000 ... 000的数字可分的情况下,同样的中等任务也正等待着我们。 因此,可分割的时期在所有方面都非常重要。
如何找到时期?
在这里,量子计算机急于向我们提供帮助。 曾几何时,在某个远古时代,一位名叫Shor的量子物理学家建议利用量子计算机来精确地找到那个时期。 实际上,量子计算机仅给出一个中间值,普通计算机随后会从中值获得一个周期,但要点并非如此,而是没有量子计算机,数学就无法计算周期。 但是,在计算期间时,我们有机会严格在期间的中间精确地计算余数的值。 为什么需要这个? 基于这一事实,您可以得出一些因子,这些因子必须包含一定值,该值是所研究数字的因数的倍数。 这是通过增加单位的其余部分并减去该单位来完成的。 可以通过快速算法跳过得到的两个数字,以找到所研究数字的最大公约数。 在至少一种情况下,我们得到了被调查人数的除数。 是的,并不是所有的事情都那么完美,因为正如我们在质数表的示例中看到的那样,在行的中间,通常会有一个被调查的数字(N-1)的加法形式,我们得到:
由此可见,在一种情况下,我们拥有研究数本身,而计算最大公因数毫无意义,在第二种情况下,我们保证了它与研究数没有公因数。 没有通用的除数,因为该数字仅比所研究的数字小2,这意味着无论哪个数字适合所研究的整数倍(将是其除数),从所研究的数字中减去它,我们都可以保证有一个较低的除数。价值比
,或使用以下公式:
这里N是一个奇数测试数(奇数是因为2的倍数可被2整除,我们不需要除以任何东西),x是N的除数,k是除法的整个结果
,m是除法的整体结果
。 也就是说,有时我们不得不改变数字系统,要求量子计算机找到一个新的时期,以期在中间会有一个更合适的数字。 加号限制是期间长度值的强制奇偶校验。 但这并没有那么可怕,因为与其他算法不同,在任何情况下,量子计算机都会计算出我们所需的长度(或数个长度),这要比宇宙的热死快得多。
尽管计算获得除数的周期与查找简单除数的任务稍有不同。 不过,我们可以在这里使用剩余表添加一些内容。 因此,这些表表明,偶数行的中间通常是一个满足以下条件的数字:
在此,r是所需的余数,而N是要研究的数字。 因此,事实证明,不需要搜索一个周期以获得数的除数,因为搜索一个周期以找到余数r,然后对其加减1。 即,您可以立即找到满足上述条件的其余部分。 的确,对这样一个值的搜索也不是一件容易的事。 但是也许量子计算机可能因为这种事情而被监禁? 量子计算专家需要了解需要多少个量子位(量子位是那些用来度量量子计算机“能力”的鹦鹉)。 尽管也许没有量子计算机也可以做到。 为此,您只需要了解哪种模式会派上用场。 一些模式在残差表中可见,但是其余读者将不得不自己弄清楚,然后您肯定会破解基于RSA的加密技术。 确实,有两个困难-首先,您需要找到这些有用的模式,然后,然后...它们可能无法付您钱。 首先,奖品是为了提供大的素数,而不是为了破解RSA。 其次,那么,想一想,世界上有多少严肃的组织有兴趣以这种方式截取他人的数据? 一些FSB(CIA,Mossad,Mi-5,仅是黑手党)发现您知道一些事情。 猜猜你会发生什么? 因此,您进一步自己承担风险和风险。
的确,量子话题本身非常有趣,因为它包含了量子不确定性,真空涨落和其他量子达尔文主义。 如何解释所有这些? 老实说,我不知道,但我看到了与其余表格的类比。 例如,当某人观察残差表中的值并且不知道先前提到的模式时,那么对于他来说,表中仅存在一些噪声,其中数字以某种随机的方式相互更改,例如真空中的某些波动。 但是,如果您了解我们只是将相同的算法应用于不同的“序列-正在研究的数字”对,那么数字中所有这些沸腾的粥将立即变得可以理解。 并且以同样的方式,很清楚为什么在用于填充表的大量可能值中,实际上仅保留严格定义的值。 但是,直到获得与所研究数字的序列“相互作用”,我们才能预测该表的内容。 更准确地说,任何填充都将同样可能。 但是,在“互动”之后,一切都将变得严格合乎逻辑,从同等概率的单一可能性中,只有一种选择会诞生。 并不是因为某种达尔文主义起作用,而是因为某种算法应用于特定的输入数据。 如果您不了解该算法,则表中的行似乎确实是达尔文风格的。 而且,如果您知道-一切都非常简单。 也许在量子物理学中,不仅需要搜索粒子,而且还需要搜索“除”的算法?
再说一次
但是,这段时间对我们来说非常重要。 是的,这是他们将在有关数学燃烧问题的热线电话中回答您的方式。 如上所示,对周期的了解使得有可能了解数字是否具有除数,或者以其他方式了解其是否为质数。 因此,我们继续这个时期。 到目前为止,我们知道许多周期属性(值的唯一性,长度均匀的对称性等),但我们不知道如何确定其长度。 尽管存在上限和下限-周期不能长于被调查的数字减去一,并且周期也不能短于数字系统的基数的增长周期,直到超过被研究的数字(7为3、11为4等)。 )。 您可以尝试应用所研究表格中已知的法则并推导出新的法则,但是到目前为止,这里有很多说明,尽管直到您尝试每一个之前,您都不会知道,大多数说明都不会成功。
因此,最有前途的方法是创建一种改进的可除性理论。 根据残基的特征序列,可以揭示许多数的可除法则。 到目前为止,仅显示了两个类(梅森数和等于数系统度的数),但实际上有无限多个。 如何处理有关所有类别数字的知识? 仅在大规模并行工作中,而不是在铁制空气加热器中,而是在人们共同完成如此大任务的形式中。 理想的结果将是创建所有数阶可除的一般理论。 这是针对初学者的,然后多项式和其他代数的除数将变为零。 但是,我们应该期望在找到质数这一任务上如此令人赞叹的人类凝聚力吗? 我怀疑不是。 因此,可悲的是,我们再次需要其他方式。
从理论上讲,有这样的方法
如果我们研究包括不同值在内的其他可分割序列,我们会发现此类序列的划分时期增长了该序列重复片段长度的倍数。 以下是形式为1010 ... 1010的可除序列的示例,其中零和一个周期性变化。 给定的序列总是划分为数制的基础,但是在这种情况下,研究周期性类的数的示例的简单性仅对我们很重要,因此我们不关注“按构造”的可分性。

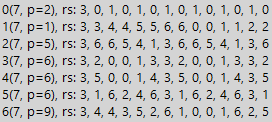
在这里,我们看到了两个数字7和上述序列的表,一个是正常的,第二个表是3的乘积。根据本示例中先前确定的模式,甚至更少,但是对于以1和6为底数的数字系统延长期限至
。 对于乘以3个表,我们看到数字系统2和5的基数的可除性损失,这本身就很有趣(可除性已从乘法变为)。 但是比这更重要。 重要的是要理解将除数表应用于任何序列的可能性。 但是为什么我们需要任何序列? 例如,增加最小可除时间。
如果最短期限可以延长,那么这使我们可以非常简单地进行素数的构建。 是的,素数无法计算,但可以通过数学方式构造。 当周期长时,一个小数除以一个大数,这意味着如果所有数字的周期都大,那么对于大数,除数只能是小数。 它有什么作用? 这使得可以通过简单搜索找到大量的所有除数。 由于小数除以大数,因此这些小数的大小帮助我们的计算机解决了大数除数无法解决的问题。 因此,寻找质数的进一步方向变得很明确-我们需要找到一个序列,该序列为我们提供了最大的最小周期。 为什么最低? 因为我们仍然不知道如何在不枚举所有残差或提高幂的情况下计算周期,因此我们无法找到一个足够长的周期(如果大于最小值),而是仅通过对残差表的分析就知道了最小值,也就是说,我们不需要。 好了,当我们找到所需的序列时(为此,我们可以使用许多此类序列的分析),我们只需选择不适合我们已知的任何最小周期的序列长度即可。 也就是说,我们将获得如此众多的数字,显然没有除数。 如果规模很大,奖品正等待着我们。 同时,我们不会对最短期限感兴趣,因为它们已经划分了非常大的数字,我们将在以后的某个时间达到。
剩下的就是找到正确的顺序。 谁来拿? 但是,即使我们找不到它,然后对于前面提到的加密,使用替代序列也可以在密码中添加另一个术语,以增加密码强度-现在,密码破解者还需要猜测我们选择的序列,该序列可以是无限个。 另外,要生成伪随机序列,我们将获得一系列残差中的值的可重复性,而不仅仅是分数周期中的一系列。
最后-奖品!
电子前沿基金会已准备好向任何人支付15万美元,然后再支付25万美元。 总计-
$ 400,000 。 那会不会打扰你? 然后到了重点! 但是事情很简单-您需要找到一个数亿个小数的质数。 这大约是3亿位,即40兆字节。 刚刚离开以超越当前记录4倍。 然后,您需要十亿个十进制数字。 这已经是400兆字节。 所有,还有两个数字-40万永远的绿色美元。
实际上,这些数字并不可怕。 现在,如果我们可以避免计算将大数除以所研究的数字而得到的余数...对于形式为100 ... 00和111 ... 111的简单序列,该度必然存在。 但是,也许对于某些序列而言,用于计算一系列残基的第i个成员的公式会更简单? 或者,您确实可以找到一个最小周期很大的序列。 毕竟,我们需要什么时期? 仅3亿(二进制形式)。 如果某个序列给我们的最小周期为100 * N,其中N是被调查的数字,那么最多300万个数字将足以让我们找到一个价值150k $的数字。 250,000美元的数字最多可获取3000万。 而现在,当短时间内可能发生的次数非常多时(对于序列100..00和111 ... 111),我们没有找到任何简单的可能性。 但是有希望,这完全取决于搜索方向的成功选择。 一次迭代一个序列对于一个人来说显然是不现实的,但是您可以尝试一下。
好吧,当您找到所需的数字时,一点官僚机构正在等待着您。 首先,您将必须在美国或英国,加拿大或澳大利亚的数学期刊上发表文章,并且该期刊应选自电子前沿基金会(EFF)列出的列表(这些期刊非常有名)。 在本文中,您必须证明您的方法确实可以找到所需的素数。 然后,您会向EFF发送一封幸福的信(在特定地址),在这里指向已发表的文章,然后等待EFF的命令。 订单可能涉及检查您为查找号码所做的一切。 不应有任何秘密,也不应有任何非法或可疑的行为。 仅此而已-您的奖金。
途中会遇到什么伏击? 好吧,对于初学者-查找质数而不要在搜索时犯错误。 接下来,您需要写一篇可靠的日记。 由于杂志是坚固的,因此编辑们对永动机的下一位发明家的来信通常是这样的:
-什么? 另一个怪胎? 到篮子!
但是您可能有写文章的经验,并且可以轻松解决此问题。 然后您会发现一张支票。 我不知道EFF将研究您的证据,但他们写道,他们可能对任何事物都感兴趣。 如果EFF目标与您提供的结果不一致,这将特别有趣。 因此,他们宣布了开发使用个人计算机的方法的目标,这些方法将其暂时用于第三方计算。
之前的奖项仅用于该程序的创建和推广,志愿者下载了该程序,从而提供了用于磨削质数的必要人字拖。EFF与没有质量terraflop的素数计算有何关系-我不知道。从理论上讲,对其要求没有任何限制,因此成功是完全可能的。就是这样,在经历了两个指示的阶段(不要忘记在零阶段找到必要的数字)之后,您便指示了将奖品转给您的银行和帐号。一大笔钱 您需要自费处理税款。而不是结尾
曾几何时,不是数学家的皮埃尔·费马(Pierre Fermat)发现了数论的许多模式。这个男人只是想知道,好吗,还有空闲时间。在这里,您所取得的成就仍然记忆犹新。另一个例子是Evarist Galois。他16岁开始学习数学,20岁时死于决斗。四年来,他一直试图使许多数学家对他的发现感兴趣,但没有成功。死后,他的工作仍然受到赞赏,而对他们来说,我们应该归功于建立这样一个数学分支,例如群论,以及代数的发展。再说一次-一个人找到星星很有趣,但是按照规则安排作品并不适合他。但幸运的是,他的工作被其他人正式化了。另一个例子-乔治·坎托(George Cantor)反映了场景的著名概念及其元素,推论出19世纪末的理论,杰出的数学家同意将其视为科学女王的基础。为什么所有这些故事?正如奥巴马先生曾经说过的:“可以!” 是的,这个美国口号非常适合热情的人们。尽管当今科学发展迅速,但它还不完整,不完美,并且其中有些地方还没有真正的科学家踏过脚。因此,让我们打开好奇心,尝试寻找这样不受限制的道路,如果成功了该怎么办?