古希腊人对是否可以用分数粗略表示非理性数字感兴趣。 证明长期存在的Duffin-Schaffer假设 ，两位数学家给出了详尽的答案。
二进制符号π是无限的。 但是，无数个分数可以以不断提高的精度接近这个数字。号码线上的深度下降并不像看起来那样牢固。 这是新的有意义的证据表明复数如何适合于简单近似的结果之一。
该证明解决了将近80年前被称为Duffin-Shaffer假设的问题。 因此，它给出了一个自上古以来数学家的最后答案：在什么条件下用22/7类型的简单分数表示无限长的无理数（例如pi）是可能的？ 证据表明，通过一次计算就可以找到这个相当普遍的问题的答案。
牛津大学的詹姆斯·梅纳德（James Maynard）是他与蒙特利尔大学的Dimitris Cuculopoulos共同提出的证明的合著者，他说：“有一个简单的标准来确定您是否可以近似于任何数字或几乎没有数字。”
数学家已经怀疑了几十年，这个简单的标准是理解何时可以获得良好逼近的关键-但他们无法证明这一点。 Cuculopoulos和Maynard仅在根据图的点和线之间的连接重新构造了数字问题之后才能够执行此操作-透视图的主要变化。
得克萨斯大学奥斯汀分校的杰弗里·沃勒说：“我想说，他们有足够的信心（而且这显然是有道理的）可以选择所选择的道路。” “干得好。”
算术醚
有了
有理数，一切就变得简单了。 它们包括用于计数对象的数字以及可以分数形式书写的所有其他数字。
由于这种能力可以被记录下来，因此我们最了解有理数。 但是，在所有
实数中，有理数实际上很少。 大多数数字是
无理数 ，具有无限的十进制表示法，并且不能以分数形式书写。 其中的一些事实证明足够重要，值得使用符号-pi，e，√2。 其余的甚至无法调用。 它们无处不在，但无法实现-就像算术以太。
因此，也许会自然而然地想一想-如果我们不能准确地表达非理性数字，那么我们可以接近它们吗？ 这是一个有理逼近的领域。 古代的数学家意识到，使用分数22/7可以很好地估算周长与直径的可比性。 后来，数学家发现了一个更精确且近似于pi的压缩近似值：355/113。
牛津大学的
本·格林说：“写pi非常困难。” “人们试图找到最精确的pi近似值，而做到这一点的常用方法之一就是使用有理数。”
1837年，
狄里克雷（Dirichlet）的数学家
彼得·古斯塔夫·勒让（Peter Gustav Lejeune）发现了一条规则，该规则告诉我们使用有理数可以准确地近似非理性数。 如果您未设置误差的确切值，则很容易找到近似值。 但是狄利克雷证明了分数，无理数和将它们分开的误差之间存在清晰的关系。
他证明 ，对于任何不合理的数字，无穷无尽的分数越来越接近他。 更准确地说，每个分数的误差将不大于1除以分母的平方。 例如，分数22/7近似表示pi，精度为1/7
2或1/49。 分数355/113与pi相距不远于1/113
2或1/12769。Dirichlet证明了存在无限多个分数，随着分母的增加，分数与pi越来越近。
蒙特利尔大学的
安德鲁·格兰维尔 （
Andrew Granville）说：“令人惊奇的和非凡的事情是能够以分数形式粗略地表示一个实数，而其误差不超过一个分数除以分母的平方。”
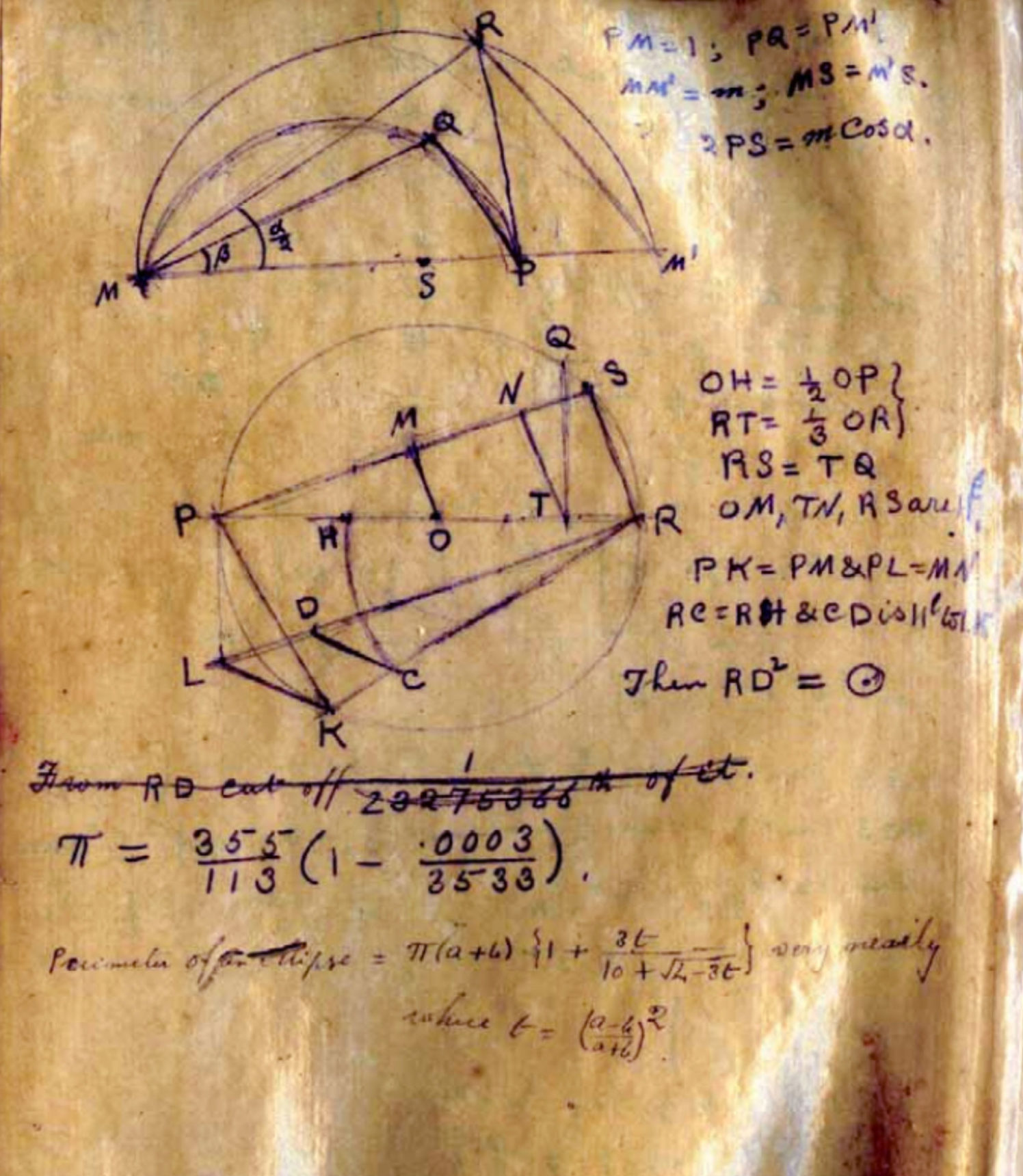在1913年的手稿中，数学家Srinivasa Ramanujan Iyengor使用分数355/113作为pi的有理近似值。Dirichlet的发现是关于有理逼近的有限陈述。 它说，对于任何无理数，如果可以使用任何整数作为分母，则可以找到无数个接近它的分数，并且您对其平方反比的大小感到满意。 但是，如果您希望分母属于某个（无限）整数子集，例如属于素数集或
全平方集，该怎么办？ 如果您希望近似误差为0.00001或具有任何其他值怎么办？ 在这样的条件下，您能否精确找到无限多个近似分数？
Duffin-Shaffer假设是试图为使用有理逼近创建最通用的平台。 1941年，数学家R.D. Duffin和A.S. Schafer提出了以下方案。 首先，选择无穷无尽的分母列表。 它可以是您想要的所有内容：奇数，可被10整除的数，质数。
然后，对于列表中的每个数字，选择您需要多大程度地近似无理数。 直觉告诉我们，如果我们选择足够大的误差，我们将有更多的近似机会。 如果选择较小的错误大小，将更加困难。 库库洛普洛斯说：“如果有足够的空间，任何顺序都会进行。”
现在，给定选定的参数-一个数字序列和一定的误差-问题出现了：是否有可能找到无穷多个近似所有无理数的分数？
假设提供了数学函数来评估该问题。 您的参数充当输入。 结果可以是两个选项之一。 Duffin和Schaffer建议，这两个选项正好对应于您的序列是否可以以所需的精度近似于几乎所有无理数，或者实际上都不是（提到“实际上”是因为对于任何分母，总会有一个小数）可以或不能很好地近似的孤立无理数）。
“您几乎得到所有东西，或者几乎一无所获。 没有中间选择，”梅纳德说。
这是一个非常笼统的陈述，试图用沿途和跨途的有理数来描述近似值。 Duffin和Schaffer提出的标准对数学家来说似乎是正确的。 但是，要证明该函数的二进制输出包含您需要的所有内容，以便了解您的逼近是否有效，那么要做起来就困难得多。
重复计算
Duffin-Schaffer假设的证明是了解您从每种可用的分母中获得了什么好处。 感觉到这一点，考虑此任务的较小版本将很有用。
假设您要近似一个0到1的线段上的所有无理数，假设所有1到10的自然数都可以用作分母，可能的分数列表非常大。 首先是1/1，然后是1/2和2/2，然后是1 / 3、2 / 3和3/3，依此类推，直到9/10和10/10。 但是，它们没有任何好处。
例如，2/10与1/5相同，而5/10与1 / 2、2 / 4、3 / 6和4/8相同。 在Duffin-Schaffer假设出现之前，苏联数学家Alexander Y. Khinchin提出了广度相似的有理逼近假设。 但是，他的定理没有考虑到等效分数应该只计算一次的事实。
Dimitris Cuculopoulos（左）和James Maynard在意大利的一次会议上介绍他的证据格兰维尔说：“通常，一年级的数学不会影响问题的解决。” “但是在这种情况下，令人惊讶的是，她影响了。”
因此，Duffin-Shaffer假设具有一个术语，用于计算每个分母的唯一分数（或简化分数）的数量。 该成员称为
Euler的
φ函数，以纪念其发明者，18世纪的数学家Leonard Euler。 φ（10）为4，因为在0和1之间只有四个分母为10的精简分数：1 / 10、3 / 10、7 / 10和9/10。
下一步是使用给定的每个分数来计算多少个无理数。 这取决于您愿意接受的尺寸错误。 Duffin-Shaffer假设使我们能够为每个分母选择一个误差。 例如，对于分母为7的分数，您可以采用0.02的允许误差。 对于分母10，可以采用误差0.01。
确定了分母和错误条件后，就该将网络置于非理性数字上了。 在0到1之间的数字线上建立分数，并从两边的分数延伸的网络形式绘制错误。 我们可以说，对于给定的条件，落入网络中的所有非理性数都是“令人满意的近似值”。 问题是：您发现了多少非理性数字？
在任何间隔的数字行中都包含无限数量的无理数，因此无法写入捕获的无理数的确切数。 取而代之的是，数学家谈论的是每个分数捕获的无理数总数中所占的比例。 他们使用诸如数字的“度量”之类的概念来评估这些比例-就像是根据重量而不是数量来估算捕获的鱼的数量。
Duffin-Schaffer假设建议将每个近似分数所捕获的无理数子集的所有度量相加。 她将此数字表示为很大的算术和。 然后，她做出了主要预测：如果这个和达到无穷大，那么您几乎可以估算出所有无理数； 如果它仅给出最终值，则不管您累加了多少个度量，那么您几乎都无法近似任何无理数。
在许多数学领域中，都出现了类似的问题，即总和“发散”到无穷大还是“收敛”到有限值。 Duffin-Shaffer假设的主要陈述是，如果您想了解是否可以使用一组给定的分母和误差来近似估计几乎所有无理数，那么您只需要知道一件事：测度的无穷大是否发散到无穷大或收敛？到最终值。
“最终，无论您如何决定评估每个分母的近似值，您的成功都完全取决于一件事：无限序列是否发散，” Waaler说。
决策制定
您可能想知道：如果一个分数近似的数字与另一个分数近似的数字相交该怎么办？ 在计算测度时，我们会不会两次考虑它们？
对于某些近似序列，重复计算并不重要。 几十年前的数学家证明，这一假设适用于由质数组成的近似序列。 但是对于许多其他近似序列，重复计数是一个问题。 因此，数学家80年来一直无法处理这个假设。
所有分母共有的简单除数的数量反映了不同分母捕获无理数的相交集合的程度。 考虑数字12和35。12的质数因子为2和3。35的质数因子为5和7。换句话说，12和35的公质因数不存在-结果，有许多无理数可以近似地乘以分母12和35不特别相交。
分母12和20呢？ 在20中，简单除数为2和5与除数12相交。以同样的方式，可以用分母为20的分数近似的无理数与可以用分母为12的分数近似的无理数相交。Duffin-Shaffer假设最难证明在这种情况下-当逼近序列中的数字有很多共同的小质数，并且每个分母近似的许多数字子集发生交集时。
“当您选择的许多分母中有许多小的简单除数时，它们就会开始互相干扰，”牛津大学的
Sam Chau说。
解决该假设的关键是找到一种方法来准确计算无理数子集的相互交叠，这是由具有共同质数因子的分母来近似的。 80年来，没有人能做到这一点。 库库洛普洛斯和梅纳德成功了，找到了关于这个问题的全新观点。
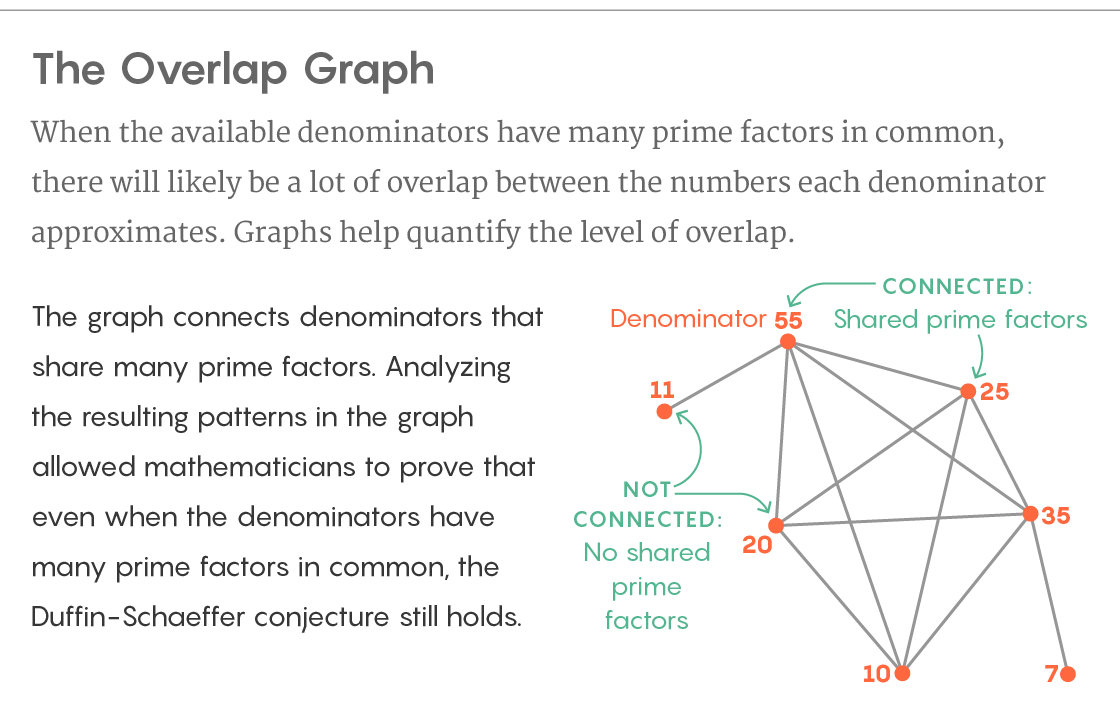相互重叠计数在他们的新证明中，他们根据分母构建了图形。 他们将它们构造为图的顶点，如果它们具有许多常见的素数除数，则将这些顶点与边连接。 图的结构描述了每个分母近似的无理数子集的叠加。 尽管很难直接研究此叠加层，但Cuculopoulos和Maynard找到了一种使用图论工具来分析图结构的方法-并以此方式找到了他们所需的信息。
Kukulopulos说：“图形有助于直观地理解任务，这是一种可以用语言反映问题的优美语言。”
Cuculopoulos和Maynard证明了Duffin-Schaffer假设确实是正确的：如果为您提供了带有有效误差的分母列表，则可以确定是否有可能近似于所有非理性数，或者仅通过检查相应的度量和是否有差异就无法做到这一点。到无穷大或收敛到有限值。
这是一个优雅的测试，它提出了关于有理数逼近性质的广泛问题，并将其简化为单个计算值。 在证明了测试的普遍性之后，库库洛普洛斯和梅纳德做了数学上最伟大的事情之一：他们为该领域的一个基本问题给出了最终答案。
格林说：“他们的证明已成为必要和充分的结果。” “我想他标志着下一章数学的结束。”