哈布雷(Habré)的“ Posit月度”已宣布为开放日,这意味着我不能错过并且忽略对他们的批评。 在先前的系列中:
一种新方法可以帮助我们摆脱浮点计算正算术:克服自己领域中的浮点数。 第一部分正算术:克服自己领域中的浮点数。 第二部分成人挑战我认为,你们中的许多人可以立即回想起至少一个历史案例,当时革命思想的形成遭到专家社区的拒绝。 通常,这种行为的缺点是已经积累了很多知识,无法以新的视角看待旧问题。 因此,新想法就失去了既定方法的特性,因为它仅由那些在开发的前一阶段被认为重要的指标来评估。
这恰恰是Posit格式今天所面临的一种厌恶:评论家通常只是简单地“朝错误的方向看”,甚至以错误的方式在实验中使用Posit。 在本文中,我将尝试解释原因。
Posit的优点已经提到了很多:数学上的优雅,低指数值的高精度,宽范围的值,仅NaN和零的一个二进制表示形式,不存在低于标准的值,与上溢/下溢的斗争。 批评者已经表达了很多:对于非常大或非常小的值都无用的准确性,复杂的二进制表示格式,当然也缺乏硬件支持。
我不想重复我已经说过的论点;相反,我将尝试着重于通常被忽略的方面。
游戏规则已更改
IEEE 754标准描述了将近40年前在Intel 8087中实现的浮点数。 以我们行业的标准来看,这是一段不可思议的时刻。 从那时起,一切都发生了变化:处理器性能,内存成本,数据量和计算规模。 Posit格式不仅是作为IEEE 754的最佳版本开发的,而且是一种用于处理符合当时新要求的数字的方法。
高层任务保持不变-我们所有人都需要在有理数域上进行有效的计算,而准确性损失最少。 但是,解决任务的条件发生了根本变化。
首先,优化的优先级已经改变。 40年前,计算机性能几乎完全取决于处理器性能。 今天,大多数计算的性能都取决于内存。 为了验证这一点,只看一下最近几十年来处理器发展的关键领域:三级缓存,推测执行,计算流水线,分支预测。 所有这些方法旨在在快速计算和缓慢访问内存的条件下实现高性能。
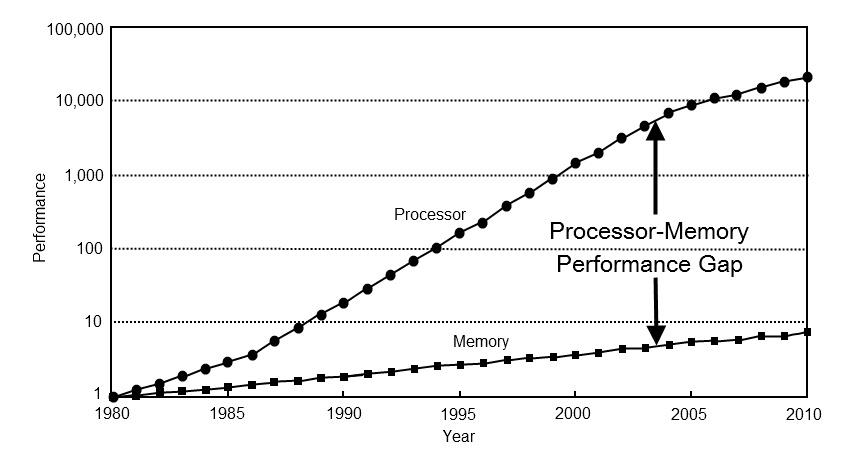
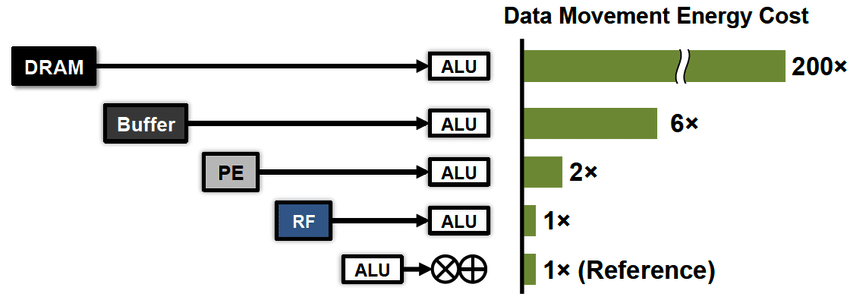
其次,新的要求已经浮出水面-有效的能源消耗。 在过去的几十年中,水平扩展计算技术已经取得了很大进步,以至于我们开始不再在乎这些计算的速度,而在乎电费。 在这里,我应该强调一个重要的部分,以便理解。 从能源效率的角度来看,计算很便宜,因为处理器寄存器与计算机非常接近。 无论是在处理器和内存之间(x100)还是在长距离(x1000 ...)上,都需要为数据传输支付更高的费用。
这只是Posit计划使用的科学项目的一个示例:

这个望远镜网络每秒产生
200 PB的数据,其处理需要
10兆瓦的小型发电厂的能量。 显然,对于此类项目,减少数据和能源消耗至关重要。
从一开始
那么Posit标准提供了什么? 要理解这一点,您需要返回到讨论的开始,并了解浮点数的精度是什么意思。
实际上有两个与准确性有关的方面。 第一个方面是
计算的
准确性 -在各种操作过程中,计算结果有多少偏差。 第二个方面是表示的
准确性 -从有理数域转换为特定格式的浮点数域时,原始值会失真多少。
现在将是一个重要的时刻。
位置主要是表示有理数的格式,而不是对有理数执行操作的方式。 换句话说,Posit是一种有损有理压缩格式。 您可能已经听说过32位Posit是64位Float的不错的选择。 因此,我们正在谈论将存储和传输同一组数字所需的数据量精确地减半。 内存减少两倍-由于对内存访问的期望较低,因此功耗和高性能几乎降低了两倍。
棍子的第二端
在这里,您应该有一个逻辑问题:如果不能以高精度执行计算,那么有效表示有理数的意义是什么?
实际上,有一种方法可以进行精确的计算,称为Quire。 这是表示有理数的另一种格式,与Posit有着千丝万缕的联系。
与Posit不同,Quire格式是专门为计算而设计的,并将中间值存储在寄存器中,而不是在主存储器中。
简而言之,Quire只是一个宽整数电池(定点算法)。 该单位以Quire的二进制表示形式对应于Posit的最小正值。 最大Quire值对应于最大Posit值。 每个Posit值在Quire中都有唯一的表示形式而不会损失准确性,但是并非每个Quire值都可以在Posit中表示而不会损失准确性。
Quire的好处是显而易见的。
它们使您以比Float更高的精度执行运算,对于加法和乘法运算,根本不会损失精度。 您必须为此付出代价的是宽处理器寄存器(es = 2的32位Posit对应于512位Quire),但这对于现代处理器而言并不是一个严重的问题。 而且,如果40年前计算超过512位整数似乎是不可接受的奢侈,那么今天,它已成为广泛访问内存的适当选择。
拼砌拼图
因此,Posit不仅以替代Float / Double的形式提供了一种新的标准,还提供了一种处理数字的新方法。 与浮动(Float)是试图在准确性,存储效率和计算效率之间寻求折衷的
单一表示形式不同,Posit提供两种不同的表示形式,一种用于存储和传输数字-本身,而另一种用于计算及其中间形式价值观-Quire。
当我们使用浮点数解决实际问题时,从处理器的角度来看,使用浮点数可以将它们表示为以下操作的集合:
- 从内存中读取数字值。
- 执行一些操作序列。 有时,操作数量很大。 在这种情况下,计算的所有中间值都存储在寄存器中。
- 将运算结果写入内存。
使用浮点/双精度时,每次操作都会失去准确性。 使用Posit + Quire,在计算过程中准确性的损失可以忽略不计。 仅在将Quire值转换为Posit的最后阶段,它才会丢失。 这就是为什么Posit + Quire的大多数“错误累积”问题根本不相关的原因。
与Float / Double不同,当使用Posit + Quire时,我们通常可以提供更紧凑的数字表示形式。 结果是-更快地从内存访问数据(更好的性能)以及更有效的信息存储和传输。
穆勒比率
作为一个视觉演示,我将仅给出一个示例-经典的穆勒递归关系,该关系是专门为演示浮点计算中的误差累积如何从根本上扭曲计算结果而发明的。

使用任意精度的算术时,应将递归序列的值减少为5。对于浮点算术,问题仅在于在哪个迭代中计算结果将开始出现不充分的偏差。
我针对IEEE 754进行了单精度和双精度以及32位Posit + Quire的实验。 计算以Quire算术进行,但是表中的每个值都转换为Posit。
实验结果
#float(32)double(64)posit(32)
------------------------------------------------
0 4.000000 4.000000 4
1 4.250000 4.250000 4.25
2 4.470589 4.470588 4.470588237047195
3 4.644745 4.644737 4.644736856222153
4 4.770706 4.770538 4.770538240671158
5 4.859215 4.855701 4.855700701475143
6 4.983124 4.910847 4.91084748506546
7 6.395432 4.945537 4.94553741812706
8 27.632629 4.966962 4.966962575912476
9 86.993759 4.980042 4.980045706033707
10 99.255508 4.987909 4.98797944188118
11 99.962585 4.991363 4.992770284414291
12 99.998131 4.967455 4.99565589427948
13 99.999908 4.429690 4.997391253709793
14 100.000000 -7.817237 4.998433947563171
15 100.000000 168.939168 4.9990600645542145
16 100.000000 102.039963 4.999435931444168
17 100.000000 100.099948 4.999661535024643
18 100.000000 100.004992 4.999796897172928
19 100.000000 100.000250 4.999878138303757
20 100.000000 100.000012 4.999926865100861
21 100.000000 100.000001 4.999956130981445
22 100.000000 100.000000 4.999973684549332
23 100.000000 100.000000 4.9999842047691345
24 100.000000 100.000000 4.999990522861481
25 100.000000 100.000000 4.999994307756424
26 100.000000 100.000000 4.999996602535248
27 100.000000 100.000000 4.999997943639755
28 100.000000 100.000000 4.999998778104782
29 100.000000 100.000000 4.99999925494194
30 100.000000 100.000000 4.999999552965164
31 100.000000 100.000000 4.9999997317790985
32 100.000000 100.000000 4.999999850988388
33 100.000000 100.000000 4.999999910593033
34 100.000000 100.000000 4.999999940395355
35 100.000000 100.000000 4.999999970197678
36 100.000000 100.000000 4.999999970197678
37 100.000000 100.000000 5
38100.000000 100.000000 5
39 100.000000 100.000000 5
40 100.000000 100.000000 5
41100.000000 100.000000 5
42100.000000 100.000000 5
43100.000000 100.000000 5
44100.000000 100.000000 5
45 100.000000 100.000000 5
46 100.000000 100.000000 5
47 100.000000 100.000000 5
48 100.000000 100.000000 5
49 100.000000 100.000000 5
50 100.000000 100.000000 5
51 100.000000 100.000000 5
52 100.000000 100.000000 5.000000059604645
53 100.000000 100.000000 5.000000983476639
54 100.000000 100.000000 5.000019758939743
55 100.000000 100.000000 5.000394910573959
56 100.000000 100.000000 5.007897764444351
57 100.000000 100.000000 5.157705932855606
58 100.000000 100.000000 8.057676136493683
59 100.000000 100.000000 42.94736957550049
60 100.000000 100.000000 93.35784339904785
61 100.000000 100.000000 99.64426326751709
62 100.000000 100.000000 99.98215007781982
63 100.000000 100.000000 99.99910736083984
64100.000000 100.000000 99.99995517730713
65 100.000000 100.000000 99.99999809265137
66 100.000000 100.000000 100
67 100.000000 100.000000 100
68100.000000 100.000000 100
69100.000000 100.000000 100
70 100.000000 100.000000 100
从表中可以看到,32位浮点数已经降到第七位,而64位浮点数一直持续到第14次迭代。 同时,使用Quire进行Posit的计算可返回多达58次迭代的稳定结果!品德
在许多实际情况下,并且如果使用得当,Posit格式实际上可以让您节省内存,比Float更好地压缩数字,另一方面,由于Quire,可以提供更好的计算精度。
但这只是一个理论! 在准确性或性能方面,在盲目相信一种方法或另一种方法之前,请务必先进行测试。 实际上,在实践中,您的特殊情况比理论上更常见。
好吧,别忘了克拉克的第一定律(自由解释):当一位受人尊敬且经验丰富的专家声称一个新的想法行得通时,他几乎是正确的。 当他声称新想法行不通时,他很可能会被误解。 我不认为自己是一位经验丰富的专家,不能让您依靠我的观点,但我请您警惕批评甚至是经验丰富且受人尊敬的人。 毕竟,魔鬼在细节中,即使有经验的人也会想念它们。