浏览器中的宇宙学和量子涨落

让我们设定一个纯粹的实际目标-实现一个能够用鼠标移动和缩放的无尽画布。 例如，这样的画布可以用作图形编辑器中的移动坐标系。 我们的想法的实现并不那么复杂，但是理解它的过程与基本的数学和物理对象相关联，我们将在开发过程中考虑这些基本对象。

问题陈述

在我们的画布上，我们只想执行两个功能：移动鼠标和移动鼠标，以及滚动时缩放。 我们转型的舞台将选择浏览器。 在这种情况下，武器不必选择。

状态机

这种系统的行为可以方便地通过其状态之间的转换来描述。 状态机 $$$\ delta：S \ rightarrow S$在哪里 $$$\ delta$-状态之间的转换函数，本身显示许多状态。

在我们的例子中，状态图如下所示：

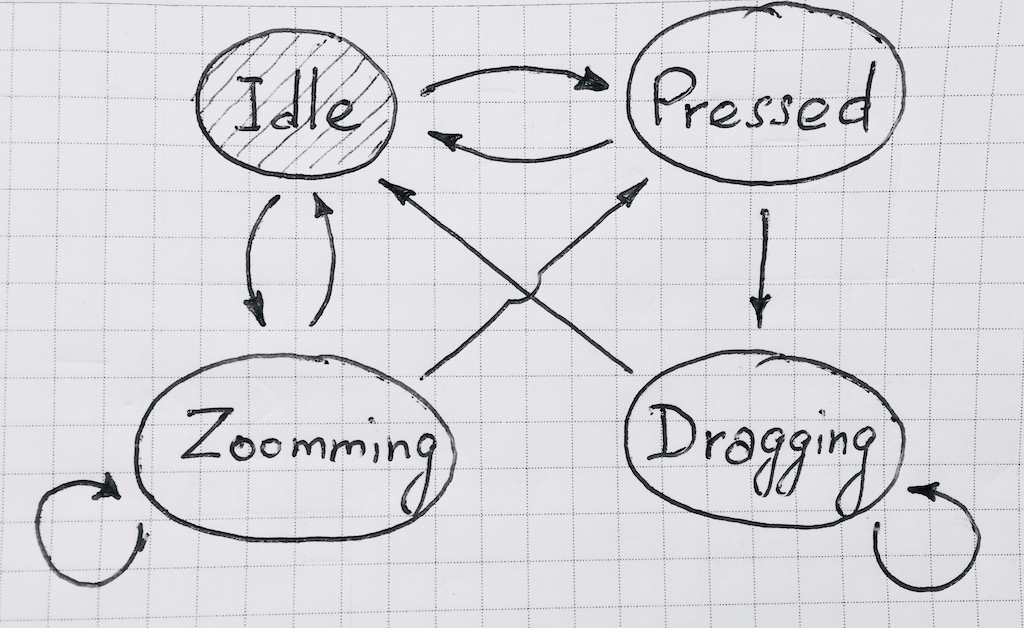
在实现过渡功能时，使事件相关变得很方便。 将来这将变得显而易见。 同样，能够订阅计算机状态的更改很方便。

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; }; 

我们将执行推迟一会儿，然后进行构成我们任务基础的几何变换。

几何形状

如果移动画布的问题非常明显，我们将不再赘述，那么应该更详细地考虑拉伸。 首先，我们需要拉伸使单个点保持静止-鼠标光标。 还必须满足可逆性条件，即 用户操作的相反顺序应将画布恢复到原始位置。 哪种几何适合于此？ 我们将考虑平面到其自身的一些点转换 $$$\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$，通常通过引入新变量来表示 $$$x'，y'$定义为旧功能：

根据数学对偶原理，这种变换可以解释为坐标系的变化，也可以解释为空间本身在固定的情况下的变换。 第二种解释对于我们的目的很方便。

对几何学的现代理解不同于对古代人的理解。 根据F. Klein的说法，-几何研究某些变换组的不变量。 因此，在一组动作中 $$$D$不变量是两点之间的距离 $$$d（（（x_ {1}，y_ {1}），（（x_ {2}，y_ {2}））= \ sqrt {（x_ {1}-x_ {2}）^ 2+（y_ {1 }-y_ {2}）^ 2}$。 它包括并行连字符 $$$T _ {（x，y）}$在向量上 $$$（x，y）$轮换 $$$R _ {\ phi}$相对于原点成一定角度 $$$\ phi$和思考 $$$M_ {l}$相对于某条线 $$$l$。 这种运动称为基本运动。 这两个运动的组成属于我们的团队，有时可以归结为基本运动。 因此，例如，相对于直线的两个连续镜面反射 $$$l$和 $$$n$围绕某个中心以某个角度旋转（请检查一下自己）：

当然您已经猜到这样的动作 $$$D$形成欧几里得几何。 但是，拉伸并不能保留两点之间的距离，而可以保留它们之间的关系。 因此，一组动作虽然应该包含在我们的方案中，但只能作为一个子组。

适合我们的几何形状基于拉伸组 $$$P$除了上述动作外，还增加了同质性 $$$S_ {k}$按系数 $$$k$。

好吧，最后。 反向元素必须存在于组中。 因此有一个中立的 $$$e$（或单个）不会更改任何内容。 举个例子

现在，我们可以用组理论语言描述拉伸，使鼠标光标固定不动：

表达运动 $$$T _ {（x，y）}$和 $$$S_ {k}$及其在代码中作为向量函数的组成

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z); 

请注意，到目前为止，我们一直在处理一组连续的转换。 但是，计算机不能处理连续量，因此，在Poincare之后，我们将连续组理解为无限的离散操作组。 现在我们已经弄清楚了几何形状，我们应该转向运动的相对性。

画布的宇宙学。 模块化网格

一个世纪以来，作为人类， 已经知道宇宙的膨胀 。 观察遥远的物体-星系和类星体，我们记录电磁频谱向更长波的移动-所谓的宇宙学红移。 任何测量都将观察者，被观察者以及与我们进行测量有关的测量方法联系起来。 如果没有测量仪器，就不可能在自然界中建立不变的关系，即确定宇宙的几何形状。 但是，几何体失去了它的意义而无法观察。 因此，在我们的任务中，最好有与银河系相关的地标，与之相关的光线可以确定画布运动的相对性。 这样的结构可以是周期性的格子，每次当空间扩展两次时，它就会分叉。

由于晶格是周期性的，因此采用模块化代数很方便。 因此，我们将作为一个团体 $$$P$也在圆环上 $$$T ^ 2 = S ^ 1 \乘以S ^ 1$。 由于监视器屏幕不是连续平面，而是整数晶格 $$$\ mathbb {Z} ^ 2$（我们现在忽略它是有限的），然后是该组的作用 $$$P$必须考虑在整数圆环上 $$$\ mathbb {Z} _ {p} ^ 2$在哪里 $$$p$-正方形边缘的大小 $$$p \倍p$：

因此，一劳永逸地将圆环固定在原点附近，我们将对其进行所有进一步的计算。 然后使用标准画布库方法传播它。 这是一个像素移动的样子：

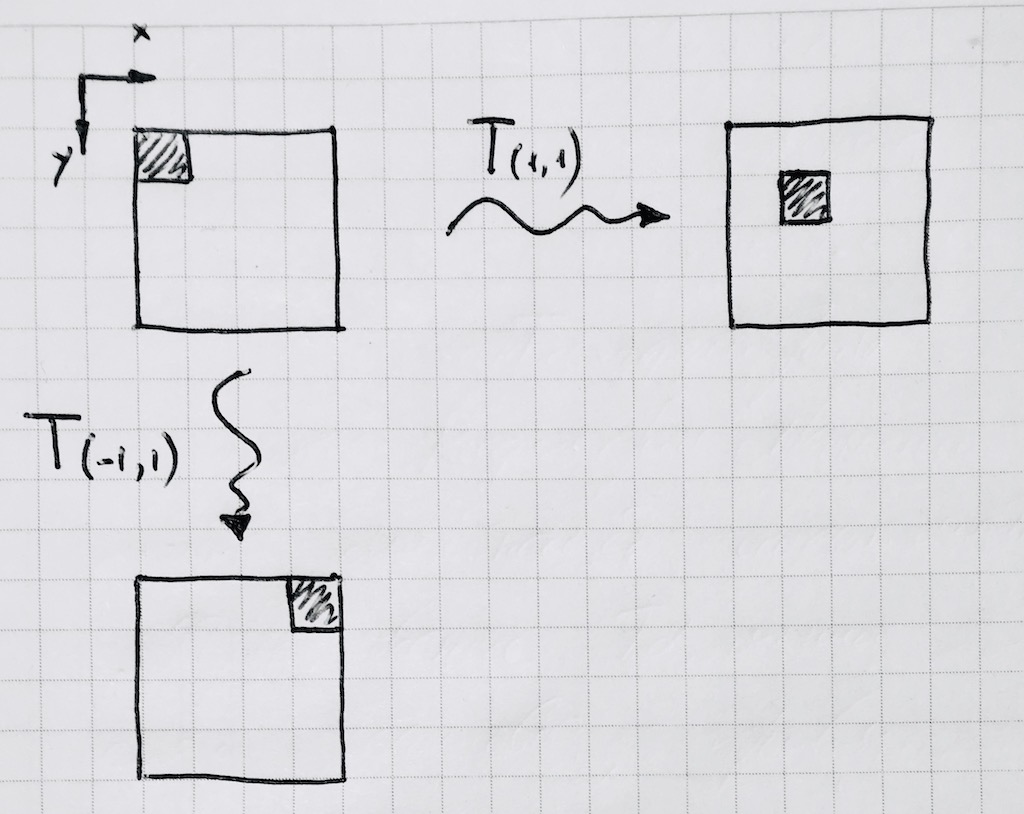
显然，采用模块x％p的标准操作不适合我们，因为它将参数的负值转换为负值，但整数环上没有任何值。 写你的功能 $$$x \ mod p$：

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p; 

现在回到最终状态机

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } } 

接下来，定义过渡方案，创建画布并

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm); 

然后，您应该确定渲染功能，设置必要的初始值并订阅状态更改。 考虑一下代码中最有趣的部分：

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); }); 

首先，我们不按系数k进行扩展，而是按nk / k的比例进行扩展。 这是由于以下事实：我们的映射在固定点处的m步 $$$（a，b）$表示为

或相对于初始值 $$$x_ {1}，y_ {1}$

显然是产品 $$$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$迭代步骤有一个非线性函数，要么很快收敛到零，要么以很小的初始偏差逃到无穷大。

我们引入变量g，这是将画布加倍的一种度量。 显然，它在一定间隔内取一个恒定值。 实现线性 $$$k_ {i} ^ *$我们使用齐次替换

然后，除第一个和最后一个成员外，工作中的所有成员将减少：

此外，相位跳变g降低了膨胀率，使得在我们之前展开的分形结构始终线性移动。 因此，我们获得了宇宙膨胀的哈勃幂定律的近似变化。

仍然需要了解我们模型准确性的局限性。

量子波动。 2 adic数字字段

了解测量过程导致了实数的概念。 海森堡的不确定性原则指出了其局限性。 现代计算机不能使用实数，而可以使用机器字，其长度取决于处理器的容量。 机器字构成2进制数的字段 $$$\ mathbb {Q_ {2}}$并表示为 $$$\ mathbb {F_ {2} ^ {n}}$在哪里 $$$n$-字长。 在这种情况下，测量过程由计算过程代替，并且与非阿基米德度量标准关联：

因此，我们的模型具有计算限制。 这些限制在IEEE_754标准中进行了描述。 从某个点开始，我们的基本大小将超出准确性的限制，并且获取模块的操作将开始生成类似于伪随机序列的错误。 只需删除该行即可验证

 if (g < min || g > max) return; 

由于我们使用多个参数，因此本例中的最终限制是通过半经验方法计算的。

结论

因此，乍看起来似乎很遥远，但理论却在浏览器的画布上联系在一起。 动作，度量和计算的概念彼此紧密相关。 合并它们的问题仍然没有解决。