关于新的革命性Posit浮点格式的利弊的讨论正在进行中。 讨论中的下一个论点是
声明 ,事实上,Posit的任务是紧凑地存储数据,而根本不用于计算。 同时,计算本身以Quire算术完成,精度更高,这也包含在Posit标准中。
好吧,那么存储。 在执行比存储格式所允许的精度更高的计算之后“存储”数字是什么意思? 这意味着四舍五入,而四舍五入意味着出错。 可以用不同的方式估算误差-为了避免重复,今天我们使用傅立叶变换进行频谱分析。
简短介绍
如果我们采用正弦曲线形式的信号并对它执行傅立叶变换,那么在频谱中我们应该得到一个峰;反之, 实际上,频谱中既可能包含谐波,其频率是由于非线性失真而获得的基音的倍数,又可能包含因噪声,干扰和数字化而获得的噪声架。 在这里,我们将测量这些噪声的水平。
开始
为了使它更加有趣,作为测试信号,我们采用的不是一个正弦波,而是多个。 必须确保这些正弦曲线的周期完全适合离散傅里叶变换的周期。 在Wolfram Mathematica中,例如,可以这样做:
sz = 8192; data = Table[2 Sum[ Sin[Prime[j] k 2 Pi/sz + j*j]/sz, {j, 100, 200, 2}] // N, {k, 0, sz - 1}];
此处使用质数表示频率的不均匀抽取。 j * j根据频率移动正弦波的相位,以避免测试信号中出现强烈的尖峰,从而为它提供或多或少的均匀振幅。 视觉接收的信号如下所示:
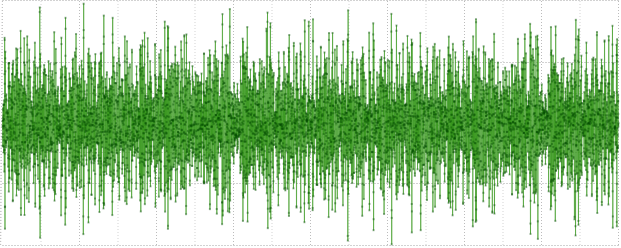
接下来,我们将其归一化为最大值,然后将其转换为整数32位Int,Float,Posit,然后再次转换为Double。 如果作者的主张是正确的,那么Double→Posit→Double转换引入的错误将更接近Doublé,而不是Float。
我们将以信号处理的标准单位分析噪声级-分贝,这使我们能够以对数标度比较值。 作为一种工具,我使用了自己的频谱分析仪,该频谱分析仪是出于研究目的而编写的。
因此:
蓝色-浮动
红色-正
紫色-Int32
蓝色-双人
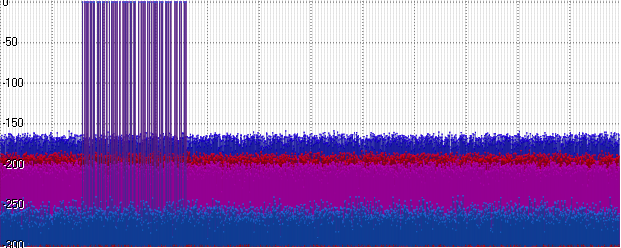
事实证明,Posit比Float要好一些-但他距离Double级别还差得很远。 同时-比Int32还差! 这是合乎逻辑的-因为部分位需要一个数量级...让我们使用此顺序-将信号的幅度增加到1000:
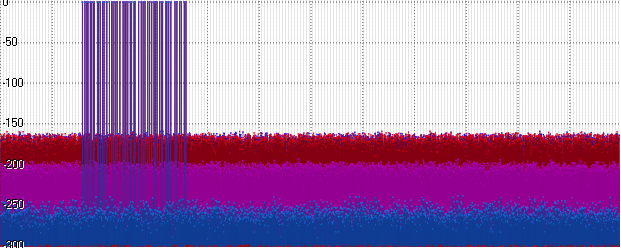
突然之间(实际上是非常预期的),Float和Posit处的噪音逐渐上升。 继续-将幅度增加到十亿:
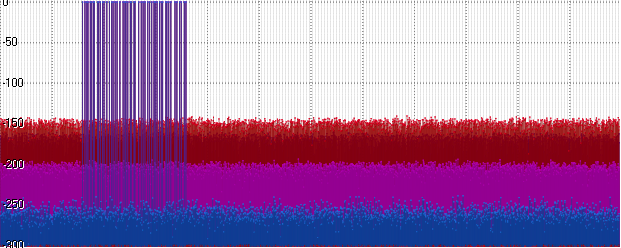
浮动显示相同的水平,并且Posit开始滞后。 振幅的进一步增加(此处为10
15 )导致噪声架子的进一步增加:
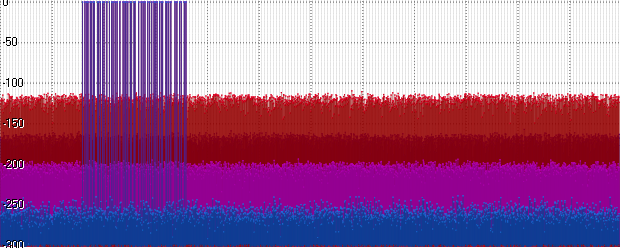
结论
奇迹仍然没有发生。 光谱分析没有证实作者的主张,即使用Posit格式存储可以提供接近Double的精度。 即使在最佳条件下,Posit的噪声架子也仅比Float低20分贝,但同时比Int32高10分贝,比Double高60分贝。
当然,Posit可以很好地找到有用的应用程序-当排放量大大超过正常值时不会导致削波或溢出的情况下,可以防止超出允许的范围。 但是即使在这种情况下,Posit的行为也更像是Int和Float之间的折衷,而不是明显更好的数字格式。