🧙🏻 💮 🕳️ 玩复数 📽️ 💰 🐮

你好

另一篇文章。这次让我们玩复数，公式及其可视化。

主意

复数是实数的一定扩展，实际上是定义了整个公理集的向量。任何复数（因此是实数）都可以写成

$z = a + bi$ 其中a是实部，b是虚部，i是等式的根

$x ^ {2} =-1$ 。为此定义了许多操作，这些操作是为实数定义的，例如，

$z_1 + z_2 = a_1 + a_2 +（b_1 + b_2）i$ 。有趣的是，如果您对它们执行各种运算，则将其加到幂，乘以等，然后取

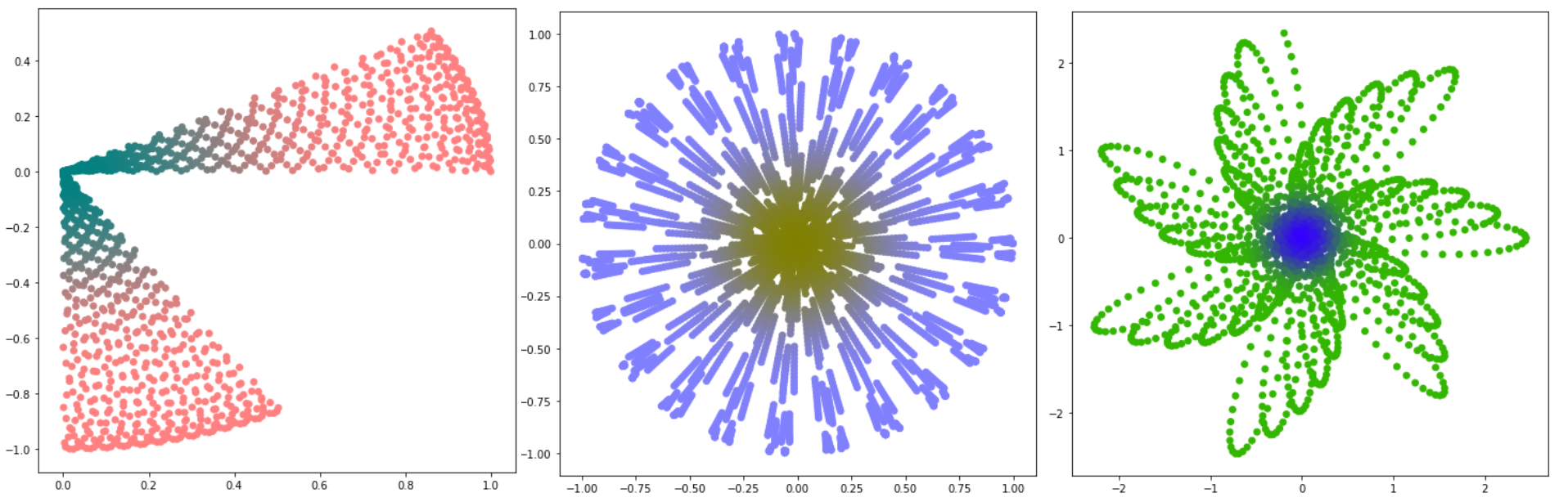
$重新（z）$ （实部）为轴Ox，并且

$Im（z）$ （虚构部分）为Oy轴，您可以获取有趣的图片。

顺便说一下，我本人想出了以下所有公式。

可视化功能

例行该函数根据此迭代函数绘制字段上的所有内容：

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show()

我们所有的函数都依赖于两个参数A和B。此外，我们在vis（）中迭代B，并且A是函数的全局参数。

卷曲功能

$f（A，B）= Bsin（B）* e ^ {iBcos（A）}$

她在python中的声明：

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))

然后跑

 A = 121.5 vis(A, func_1, step=0.1)

对于A = 121.5的结果：

对于A = 221.5：

请注意，这些数字并非来自对光滑流形上任何定积分的计算以及其他在此上下文中没有意义的聪明单词。这些实际上是随机数，并且仍然存在完全不同的A，从而获得了美丽。

需要油漆

我们声明一个颜色函数（这种函数返回坐标中三个数字的元组）：

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5)

选择随机参数A，使其为149：

 vis(149, func_1, step=0.1, c=color_1)

鹅功能

鹅的描述如下：

$f（A，B）= cos（B）sin（B）* B * e ^ {iBcos（A）}$

Python声明：

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))

对于A = 106的结果：

Focaccia功能

$f（A，B）= cos（B（A + 1））* e ^ {iBcos（A）}$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A)))

 vis(246, func_3, step=0.1, c=color_2)

 vis(246, func_3, step=0.1, c=color_2)

无标题功能

$f（A，B）= Bsin（A + B）* e ^ {iBsin（A）}$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3)

 vis(179, func_4, step=0.1, c=color_3)

美容配方

$f（A，B）= cos（B（A + 1））^ {\ frac {3} {2}} * e ^ {iBcos（A）}$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A)))

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4)

 vis(350, func_5, step=0.1, c=color_4)

现在就这些了。

整个代码

 import numpy as np import random import matplotlib.pyplot as plt import math def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[7, 7]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) def func_4(A, B): return math.sin(A + B) * B * math.e ** (1j * B * math.sin(A)) def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) def sigm(x): return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) colors = [color_1, color_2, color_3, color_4] funcs = [func_1, func_2, func_3, func_4, func_5] while True: col = random.choice(colors) func = random.choice(funcs) vis(random.random() * 200 + 100, func, step=0.1, c=col) if input() == "exit": break

更多截图

玩复数

主意