我的名字叫维亚切斯拉夫（Vyacheslav），我是位长期数学家，多年来，我在使用数组时没有使用过循环...
正是因为我在NumPy中发现了向量运算。 我想向您介绍我最常用于处理数据和图像数组的NumPy函数。 在文章的结尾，我将展示如何使用NumPy工具包对图像进行卷积而无需迭代（非常快）。
不要忘记
import numpy as np
走吧！
目录内容
什么是numpy？数组创建访问元素，切片数组的形状及其变化轴重排和换位数组联接资料克隆数组元素的数学运算矩阵乘法聚合器而不是结论-一个例子什么是numpy？
这是一个与SciPy项目分开的开源库。 NumPy是Numeric和NumArray的后代。 NumPy基于以Fortran编写的LAPAC库。 Matlab是NumPy的非python替代方案。
由于NumPy基于Fortran，因此它是一个快速的库。 并且由于它支持多维数组的矢量运算，因此非常方便。
除了基本版本（基本版本中的多维数组）之外，NumPy还包括一组用于解决特殊任务的软件包，例如：
- numpy.linalg-实现线性代数的运算（在基本版本中，向量和矩阵的简单乘法）；
- numpy.random-实现用于处理随机变量的函数；
- numpy.fft-实现直接和逆傅立叶变换。
因此，我建议仅详细考虑一些NumPy功能及其使用示例，这足以让您了解此工具的功能！
<上>数组创建
有几种创建数组的方法：
- 将列表转换为数组：
A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
- 复制数组（需要复制和深度复制！）：
B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
- 创建一个零或一个给定大小的数组：
A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]])
B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])
或采用现有阵列的尺寸：
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]])
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])
- 创建二维正方形数组时，可以使其成为单位对角矩阵：
A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
- 使用Step步骤构建一个从From（包括）到To（不包括）的数字数组：
From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])
默认情况下，from = 0，step = 1，因此具有一个参数的变量解释为To：
A = np.arange(5) A Out: array([0, 1, 2, 3, 4])
或使用两个-如从和到：
A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])
请注意，在方法3中，数组的尺寸作为
一个参数（尺寸的元组）传递。 方法3和4中的第二个参数，您可以指定所需的数组元素类型：
A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]])
B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])
使用astype方法，可以将数组转换为其他类型。 所需类型表示为参数：
A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')
所有可用的类型都可以在sctypes词典中找到：
np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}
<上>访问元素，切片
对数组元素的访问由整数索引执行，倒数从0开始：
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5
如果您将多维数组想象成嵌套的一维数组（线性数组，其元素可以是线性数组）的系统，那么很明显，您可以使用一组不完整的索引来访问子数组：
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])
有了这种范例，我们可以重写访问一个元素的示例：
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5
当使用一组不完整的索引时，缺少的索引会隐式地替换为沿相应轴的所有可能索引的列表。 您可以通过设置“：”来明确地做到这一点。 上一个带有一个索引的示例可以重写如下：
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])
您可以沿任何一个或多个轴跳过索引；如果该轴后跟带有索引的轴，则“：”必须：
A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])
索引可以采用负整数值。 在这种情况下，计数从数组末尾开始：
A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4
您不能使用单个索引，而可以使用沿每个轴的索引列表：
A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])
或索引范围为“从：到：步骤”的形式。 这种设计称为切片。 根据索引列表选择所有元素，从包括索引（从包括索引）到不
包括步骤步骤的到索引：
A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])
索引步骤的默认值为1，可以跳过：
A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
From和To值也具有默认值：0和沿索引轴的数组大小分别为：
A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])
如果要默认使用From和To（此轴上的所有索引）并且step不同于1，则需要使用两对冒号，以便解释器可以将单个参数标识为Step。 以下代码沿第二个轴“扩展”数组，但沿第一个轴不变：
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
现在开始吧
print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]
如您所见，通过B，我们更改了A中的数据。这就是为什么在实际任务中使用副本很重要的原因。 上面的示例应如下所示：
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
NumPy还提供了通过布尔索引数组访问多个数组元素的功能。 索引数组必须与索引数组的形状匹配。
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])
如您所见，这种构造将返回一个平面数组，该数组由对应于真实索引的索引数组的元素组成。 但是，如果我们使用对数组元素的这种访问方式来更改其值，则将保留数组的形状：
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]
在索引布尔数组上定义逻辑运算逻辑_，逻辑或或逻辑非，并按元素执行逻辑运算AND，OR和NOT：
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]
logical_and和logical_or取2个操作数，logic_not不取1。 您可以使用运算符＆，|。 和〜分别使用任意数量的操作数执行AND，OR和NOT：
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]
等效于仅使用I1。
通过写入以数组名称作为操作数的逻辑条件，可以获得与值数组形式相对应的索引逻辑数组。 索引的布尔值将作为对应数组元素的表达式的真值进行计算。
查找I元素的索引数组，该元素大于3，并且值小于2且大于4的元素将被重置为零：
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]
<上>数组的形状及其变化
多维数组可以表示为最大长度的一维数组，该数组沿最后一个轴的长度切成碎片，并从轴开始沿轴分层放置。
为了清楚起见，请考虑一个示例：
A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]
在此示例中，我们从一个长度为24个元素的一维数组中形成了2个新数组。 数组B，大小为4 x6。如果查看值的顺序，则可以看到沿第二维有连续值的链。
在数组C中，4×3×2，连续值沿最后一个轴运行。 沿着第二个轴是串联的块，这些块的组合将导致沿着数组B的第二个轴排成一行。
鉴于我们没有制作副本，因此很明显，这些副本是同一数据数组的不同表示形式。 因此，您可以轻松快速地更改数组的形状，而无需更改数据本身。
要找出数组的维数（轴数），可以使用ndim字段（数），并找出沿每个轴的大小-形状（元组）。 尺寸也可以通过形状的长度来识别。 要找出数组中元素的总数，可以使用size值：
A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24
注意ndim和shape是属性，不是方法！
要查看一维数组，可以使用ravel函数：
A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])
要沿轴或尺寸调整大小，请使用reshape方法：
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])
保留元素的数量很重要。 否则，将发生错误：
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)
假定元素的数量是恒定的，则可以根据沿其他轴的长度值来计算整形时沿任一轴的大小。 沿一个轴的尺寸可以指定为-1，然后将自动计算：
A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)
您可以使用reshape而不是ravel：
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)
考虑某些功能在图像处理中的实际应用。 作为研究的对象，我们将使用照片：
让我们尝试使用Python下载和可视化它。 为此，我们需要OpenCV和Matplotlib：
import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()
结果将是这样的：
注意下载栏：
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)
OpenCV处理BGR格式的图像，并且我们熟悉RGB。 我们沿色轴更改字节顺序，而无需使用该结构访问OpenCV函数
“ [：，：，:: :: 1]”。
在每个轴上将图像缩小2倍。 我们的图像分别沿轴具有均匀的尺寸，可以在不进行插值的情况下进行缩小：
I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()
改变数组的形状，我们得到了2个新轴，每个轴有2个值，它们对应于由原始图像的奇数行和偶数行和列组成的帧。
由于使用Matplotlib导致质量不佳，因为在那里您可以看到轴向尺寸。 实际上，缩略图的质量为：
<上>轴重排和换位
除了使用相同顺序的数据单元更改阵列的形状外，通常还需要更改轴的顺序，这自然会导致数据块的排列。
这种转换的一个例子是矩阵的转置：交换行和列。
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]
在此示例中，使用AT构造对矩阵A进行转置。转置运算符反转轴顺序。 考虑另一个具有三个轴的示例：
C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]
这个简短的条目有一个较长的副本：np.transpose（A）。 这是更换轴顺序的功能更广泛的工具。 第二个参数允许您指定源数组的轴号元组，该元组确定它们在结果数组中的位置顺序。
例如，重新排列图像的前两个轴。 图片应翻转，但色轴保持不变：
I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()
对于此示例，可以使用另一个交换工具。 此方法互换参数中指定的两个轴。 上面的示例可以这样实现：
I_ = np.swapaxes(I, 0, 1)
<上>数组联接
合并的数组必须具有相同数量的轴。 数组可以与新轴的组合或沿现有轴的组合来组合。
为了与新轴的形成相结合，原始数组在所有轴上的尺寸必须相同：
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])
从示例中可以看到，操作数数组成为新对象的子数组，并沿新轴排列，这是第一个顺序。
要沿现有轴合并数组，除了选择用于连接的轴外，所有轴上的大小都必须相同，并且沿其可以有任意大小：
A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])
要沿第一轴或第二轴合并，可以分别使用vstack和hstack方法。 我们以图像为例进行说明。 vstack组合高度相同宽度的图像，而hsstack组合宽度相同的高度图像：
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()
请注意，在本节的所有示例中，连接的数组都是通过一个参数（元组）传递的。 操作数的数量可以是任意数量，但不一定是2。
还要注意合并数组时内存的变化：
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]
由于创建了新对象，因此将从原始数组中复制其中的数据，因此新数据中的更改不会影响原始对象。
<上>资料克隆
np.repeat（A，n）运算符将返回一维数组，其中包含数组A的元素，每个元素将重复n次。
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]
进行此转换后，您可以重建数组的几何形状并在一个轴上收集重复的数据：
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]
此选项仅在相同数据所在的轴位置上不同于将数组与堆栈运算符本身组合在一起。 在上面的示例中，如果使用堆栈，则这是最后一个轴-第一个：
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]
无论如何克隆数据，下一步都是将轴上具有相同值的轴移动到轴系统的任何位置：
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]
如果要使用元素重复来“拉伸”任何轴，则必须将具有相同值的轴放在可扩展对象之后（使用转置），然后将这两个轴组合在一起（使用重塑形状）。 考虑一个通过复制行沿垂直轴拉伸图像的示例：
I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1]
<上>数组元素的数学运算
如果A和B是相同大小的数组，则可以对它们进行加，乘，减，除并求幂。 这些操作是
逐个元素执行
的 ，结果数组的几何形状将与原始数组重合，并且每个元素都是对原始数组中的一对元素进行相应操作的结果：
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]
您可以从上面对数组和编号执行任何操作。 在这种情况下，该操作还将在数组的每个元素上执行：
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]
考虑到多维数组可以看作是平面数组（第一轴），其元素是数组（其他轴），因此，当几何B与子数组A的几何沿第一方向固定时，可以对数组A和B进行考虑的操作。 换句话说，具有相同数量的轴和大小A [i]和B。在这种情况下，每个数组A [i]和B将是在数组上定义的操作的操作数。
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]
在此示例中，数组B受到数组A的每一行的操作。如果您需要沿另一条轴乘/除/加/减/提高子阵列的度数，则必须使用转置将所需的轴放在其第一位，然后将其放回原位。 考虑上面的例子，但是乘以数组B的列的向量B：
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]
对于更复杂的函数（例如，三角函数，指数，对数，度与弧度之间的转换，模数，平方根等），NumPy具有实现。考虑指数和对数的示例： A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]
在此处可以找到NumPy中数学运算的完整列表。<上>矩阵乘法
数组乘积的上述操作是逐元素执行的。并且，如果您需要按照线性代数规则对数组进行张量运算，则可以使用点（A，B）方法。根据操作数的类型，函数将执行：- 如果参数是标量（数字），则将执行乘法；
- 如果参数是向量（一维数组）和标量，则该数组将乘以一个数字；
- 如果参数是向量，则将执行标量乘法（元素乘积之和）；
- 如果参数是张量（多维数组）和标量，则向量将乘以一个数字；
- 如果张量的自变量，则将执行沿着第一个自变量的最后一个轴和倒数第二个的张量的乘积；
- 如果参数是矩阵，则执行矩阵的乘积（这是张量积的特例）；
- 如果参数是矩阵和向量，则将执行矩阵和向量的乘积（这也是张量积的特殊情况）。
要执行这些操作，相应的大小必须重合：对于长度向量，对于张量，沿着将对各个元素乘积进行累加的轴的长度。考虑带有标量和向量的示例：
使用张量，我们将只看结果数组的几何尺寸如何变化：
要使用其他轴而不是为点定义的轴执行张量积，可以将tensordot与显式轴一起使用： A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)
我们已经明确指出，我们使用第一个数组的第三个轴，使用第二个数组的第二个轴（沿这些轴的大小必须匹配）。<上>聚合器
聚合器是NumPy方法，使您可以沿某些轴替换具有整体特征的数据。例如，您可以计算沿任何一个或多个轴的平均值，最大值，最小值，变化率或其他特征，并根据此数据形成一个新数组。新阵列的形状将包含原始阵列的所有轴，但沿其计算聚合器的轴除外。例如，我们将形成一个具有随机值的数组。然后，在其列中找到最小值，最大值和平均值： A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]
通过这种用法，均值和平均值看起来像同义词。但是这些功能具有一组不同的附加参数。掩蔽和加权平均数据有不同的可能性。您可以在多个轴上计算积分特性： A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
在此示例中，考虑了另一个积分特征总和-总和。聚合器列表如下所示：- sum：sum和nansum-使用nan正确管理的变体；
- 工作：prod和nanprod；
- 平均值和期望值：平均值和均值（nanmean），没有
nanaverage； - 中位数：中位数和中位数；
- 百分位：百分位和百分位；
- 变体：var和nanvar;
- 标准偏差（方差的平方根）：std和nanstd；
- : min nanmin;
- : max nanmax;
- , : argmin nanargmin;
- , : argmax nanargmax.
在使用argmin和argmax的情况下（分别使用nanargmin和nanargmax），必须指定一个将考虑特性的轴。如果未指定轴，则默认情况下将在整个数组中考虑所有考虑的特性。在这种情况下，argmin和argmax也将正常工作，并找到最大或最小元素的索引，就好像使用ravel（）命令沿同一轴拉伸了数组中的所有数据一样。还应注意，聚合方法不仅定义为NumPy模块的方法，而且还定义为数组本身：入口np.aggregator（A，轴）等效于入口A.aggregator（轴），其中，aggregator表示上述功能之一，通过axes-轴索引。 A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
<上>而不是结论-一个例子
让我们构建一个用于线性低通图像滤波的算法。首先，请上传嘈杂的图像。
考虑一下图像的片段以查看噪声：
我们将使用高斯滤波器对图像进行滤波。但是，我们不直接进行卷积（使用迭代），而是对彼此偏移的图像切片进行加权平均： def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J
我们将此功能一次，两次和三次应用于我们的图像： I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)
我们得到以下结果：
一次性使用过滤器；
双
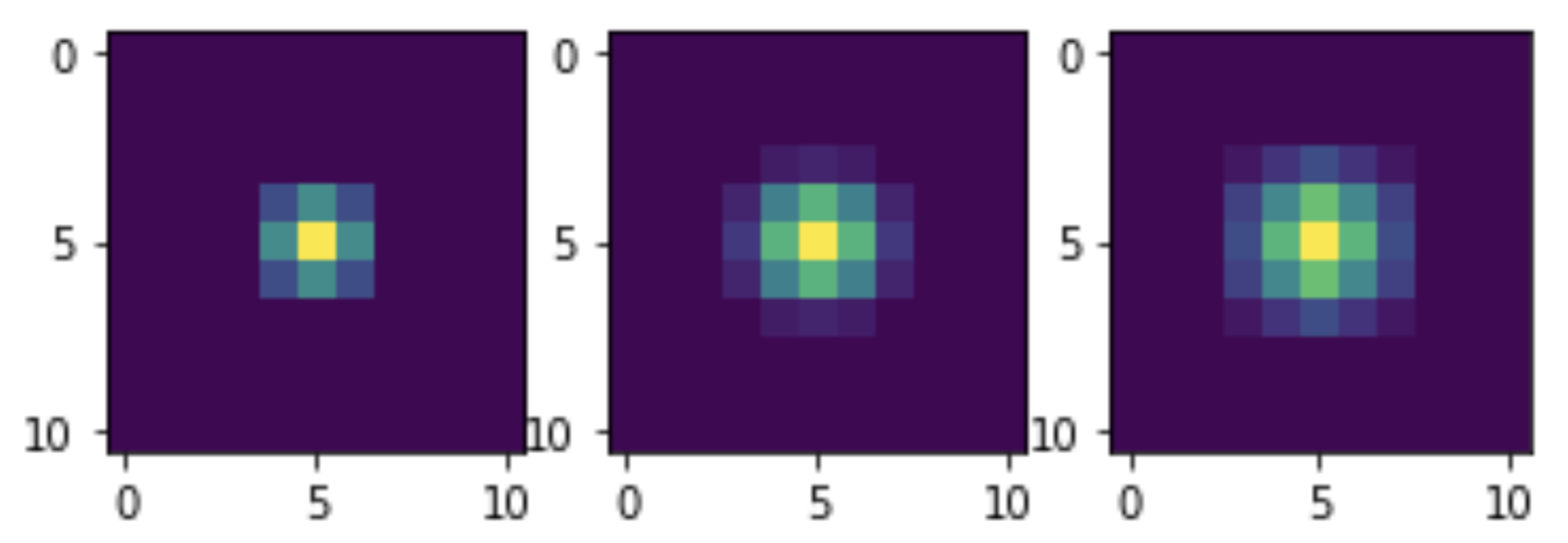
在三倍。可以看出，随着滤波器通过次数的增加，噪声水平降低。但这也会降低图像的清晰度。这是线性滤波器的一个已知问题。但是我们的图像去噪方法并不声称是最优的：这只是NumPy无需迭代即可实现卷积功能的证明。现在让我们看一下我们的过滤等效的内核卷积。为此，我们将对单个单位脉冲进行类似的转换并进行可视化。实际上，由于混合本身针对整数数据进行了优化，因此脉冲不会是单个脉冲，而是振幅等于255。但这不会干扰评估核的一般外观： M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()
我们考虑的NumPy功能远非完整，我希望这足以证明此工具的全部功能和美感！<上>