哦，牛顿的方法

关于数值优化方法的文章很多。 这是可以理解的，尤其是在深度神经网络最近展示的成功背景下。 令人欣慰的是，至少一些发烧友不仅对如何在已经流行于这些Internet的框架上轰炸他们的神经网络感兴趣，而且对它们如何工作以及为什么起作用感兴趣。 但是，我最近不得不指出，在提出与神经网络训练有关的问题时（不仅与训练有关，而且不仅与网络有关），包括在哈布雷（Habré）上，越来越多地使用许多“知名”语句进行转发，其有效性简单地说，令人怀疑。 在这些可疑的陈述中：

1. 在训练神经网络的任务中，二阶或更多阶的方法效果不佳。 因为那样
2. 牛顿法需要正弦确​​定性的Hessian矩阵（二阶导数），因此效果不佳。
   
3. Levenberg-Marquardt方法是梯度下降和Newton方法之间的折衷，通常是启发式的。
   

等 与继续这份名单相比，开始做生意最好。 在这篇文章中，我们将考虑第二个陈述，因为我在哈布雷至少只见过他两次。 我将仅在涉及牛顿法的部分中提及第一个问题，因为它的范围要广得多。 第三和其余的将留给更好的时间。

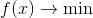
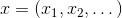
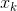
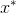
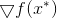
我们关注的焦点将是无条件优化的任务 在哪里 -向量空间的一个点，或者干脆-向量。 当然，我们了解的越多，这项任务就越容易解决 。 通常认为每个参数都有区别 ，以及我们肮脏的事所需的次数。 众所周知，这一点的必要条件 达到最小值，是函数的梯度相等 此时为零。 从这里，我们立即获得以下最小化方法：

解方程 。

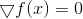
温和地说，这项任务并不容易。 绝对不比原来容易。 但是，在这一点上，我们可以立即注意到最小化问题和求解非线性方程组问题之间的联系。 在考虑使用Levenberg-Marquardt方法时（当我们使用它时），这种联系会重新出现。 同时，请记住（或发现）牛顿法是求解非线性方程组的最常用方法之一。 它在于以下事实： 我们从一些初始近似开始 建立一个序列

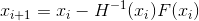
-牛顿的显式方法

或

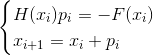
-牛顿的隐式方法

在哪里 -由函数的偏导数组成的矩阵 。 自然，在一般情况下，当简单地将非线性方程组简单地带给我们时，就需要从矩阵中得到一些东西。 我们没有资格。 在方程是某个函数的最小条件的情况下，我们可以说矩阵 对称的。 但没有更多。

牛顿法求解非线性方程组的方法已得到很好的研究。 这就是问题-对于其收敛，不需要矩阵的正定性 。 是的，并且不需要，否则他将一文不值。 取而代之的是，还有其他条件可以确保这种方法的局部收敛，在此我们将不予考虑，从而将感兴趣的人员吸引到专业文献中（或在评论中）。 我们得到陈述2为假。

那呢

是的，没有。 这个词的伏击是该词之前的局部收敛。 这意味着初始近似 必须与解决方案“足够近”，否则在每个步骤中，我们都将越来越远。 怎么办 我不会详细介绍如何解决一般形式的非线性方程组的问题。 相反，回到我们的优化任务。 陈述2的第一个错误实际上是通常说到优化问题中的牛顿法，这意味着它的修改-阻尼牛顿法，其中根据规则构造了近似序列。

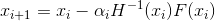
-牛顿的显式阻尼方法

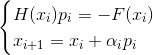
-牛顿的隐式阻尼方法

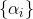
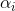
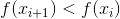
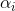
这是顺序 是该方法的参数，其构造是单独的任务。 在最小化问题中，选择时自然 要求在每次迭代中函数f的值减小，即 。 逻辑上出现了一个问题：是否存在这样的（正面） ？ 如果这个问题的答案是肯定的，那么 称为下降方向。 然后可以通过以下方式提出问题：
牛顿法生成的方向何时是下降方向？
要回答这个问题，您将不得不从另一侧看待最小化问题。

下降方法

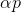
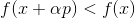
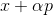
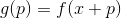
对于最小化问题，此方法似乎很自然：从任意点开始，我们以某种方式选择方向p并朝该方向迈出一步 。 如果 然后拿 作为新的起点，然后重复该过程。 如果方向是任意选择的，那么这种方法有时称为随机游走法。 可以将单位基向量作为方向-即，仅在一个坐标中迈出一步，该方法称为坐标下降法。 不用说，它们无效吗？ 为了使此方法正常工作，我们需要一些额外的保证。 为此，我们引入了辅助功能 。 我认为最小化很明显 完全等同于最小化 。 如果 然后可区分 可以表示为



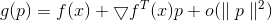
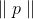
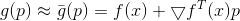
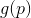
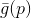
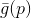
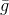
如果 那么小 。 我们现在可以尝试替换最小化问题 使其近似值（或模型 ）最小化的任务 。 顺便说一下，所有基于使用方法的模型 称为渐变。 但是麻烦是 是线性函数，因此没有最小值。 为了解决此问题，我们对要执行的步骤的长度添加了限制。 在这种情况下，这是完全自然的要求-因为我们的模型或多或少正确地仅在足够小的邻域中描述了目标函数。 结果，我们获得了条件优化的另一个问题：



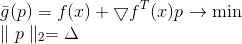
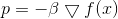
此任务有一个明显的解决方案： 在哪里 -保证满足约束条件的因素。 然后，下降法的迭代形式为

，

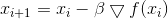
在其中我们学习了著名的梯度下降法 。 参量 ，通常称为下降速度，现在已经具有可以理解的含义，其值是根据新点位于给定半径的球体上（围绕旧点外接）的条件确定的。

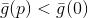
根据目标函数构造模型的性质，我们可以认为 ，即使很小，如果 然后 。 值得注意的是，在这种情况下，我们的移动方向并不取决于该球体半径的大小。 然后，我们可以选择以下方式之一：

1. 根据某种方法选择值 。
2. 设置选择适当值的任务 ，从而降低了目标函数的值。

第一种方法是信任区域方法的典型方法 ，第二种方法导致了所谓的辅助问题的形成。 线性搜索（LineSearch） 。 在这种特殊情况下，这些方法之间的差异很小，我们将不予考虑。 相反，请注意以下几点：

为什么我们实际上在寻找补偿 恰好躺在球上？

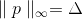
实际上，我们可以用这样的要求很好地替换此限制，例如，p属于立方体的表面，即， （在这种情况下，它不太合理，但是为什么不这样）或某些椭圆形的表面呢？ 如果我们回想起最小化沟壑功能时出现的问题，这似乎已经很合逻辑了。 问题的实质是，沿着某些坐标线，函数的变化比沿着其他坐标线的变化快得多。 因此，我们得到如果增量应属于球体，则数量 提供“下降”的位置应该很小。 这导致一个事实，即达到最低要求将需要大量步骤。 但是，如果相反，我们采用合适的椭圆作为邻域，那么这个问题将神奇地化为泡影。

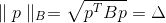
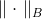
在椭圆面的点属于的条件下，可以写成 在哪里 是一些正定矩阵，也称为度量。 规范 称为由矩阵引起的椭圆范数 。 这是什么样的矩阵，以及从哪里获得的矩阵-我们将在以后考虑，现在我们开始一项新任务。



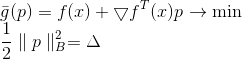
规范的平方和1/2系数在这里仅仅是为了方便起见，以免混淆根源。 应用拉格朗日乘数法，我们得到了无条件优化的有界问题



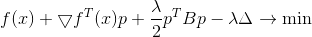
最低要求的必要条件是

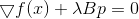
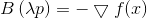
或 从哪里来







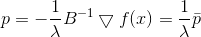
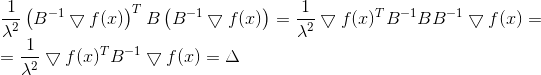
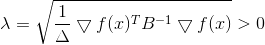
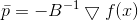
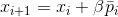
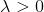
再次，我们看到了方向 ，我们将在其中移动，而不取决于值 -仅从矩阵 。 再说一次，我们可以接载 充满了计算的需要 和显式矩阵求逆 ，或解决寻找合适偏差的辅助问题 。 由于 ，可以保证存在对此辅助问题的解决方案。

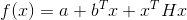
那么矩阵B应该是什么呢？ 我们将自己局限于投机性思想。 如果目标函数 -二次方，即具有形式 在哪里 正定，很明显，矩阵作用的最佳人选 是粗麻布的 ，因为在这种情况下，我们需要构造下降法的一个迭代。 如果H不是正定的，则​​它不能是度量，并且以此构造的迭代是阻尼牛顿法的迭代，但不是下降法的迭代。 最后，我们可以给出严格的答案

问题： 牛顿法中的黑森矩阵是否必须是正定的？
答： 不，在标准牛顿法或阻尼牛顿法中都不需要。 但是，如果满足此条件，则阻尼牛顿法是一种下降法，具有全局性质 ，而不仅仅是局部收敛。

作为说明，让我们看一下使用梯度下降和牛顿方法将众所周知的Rosenbrock函数最小化时的置信度区域，以及区域的形状如何影响过程的收敛。



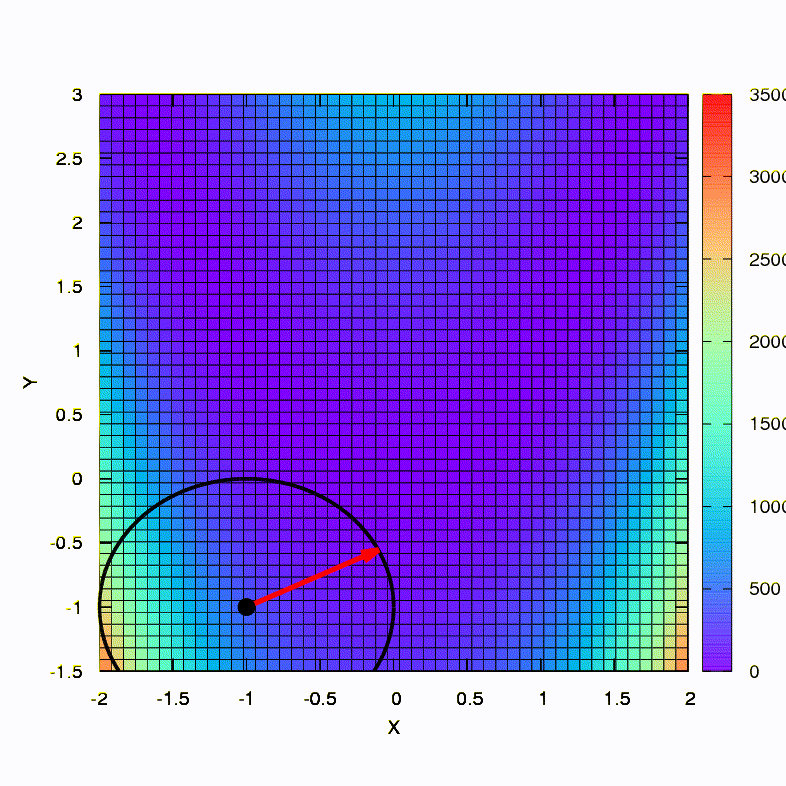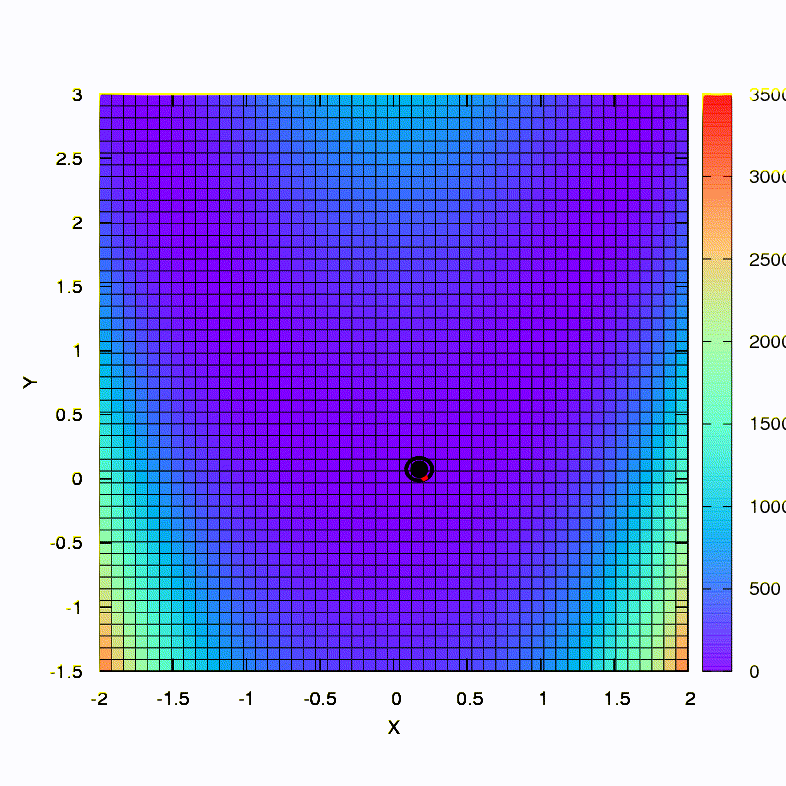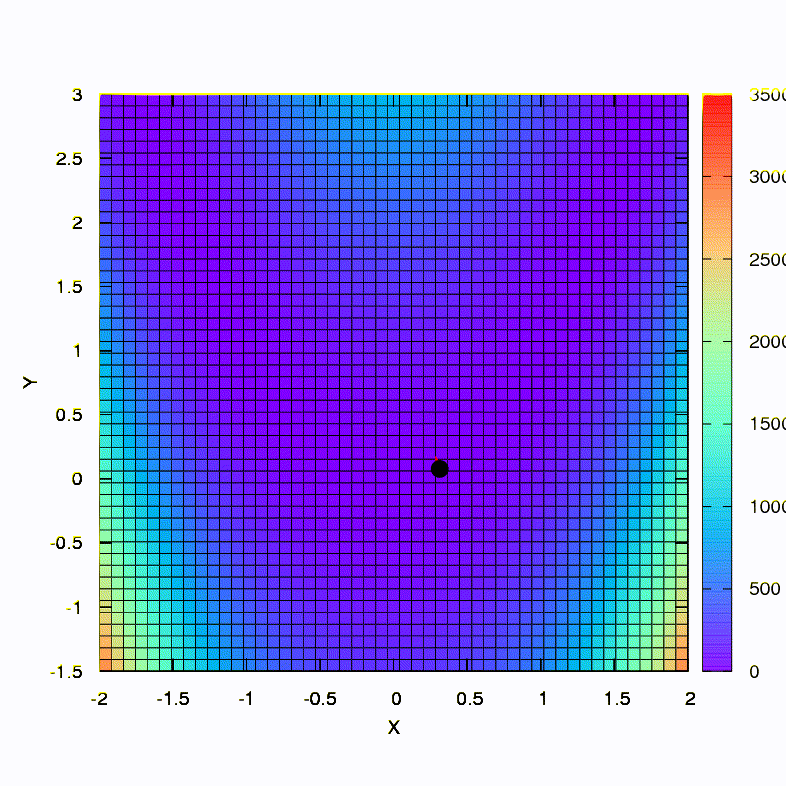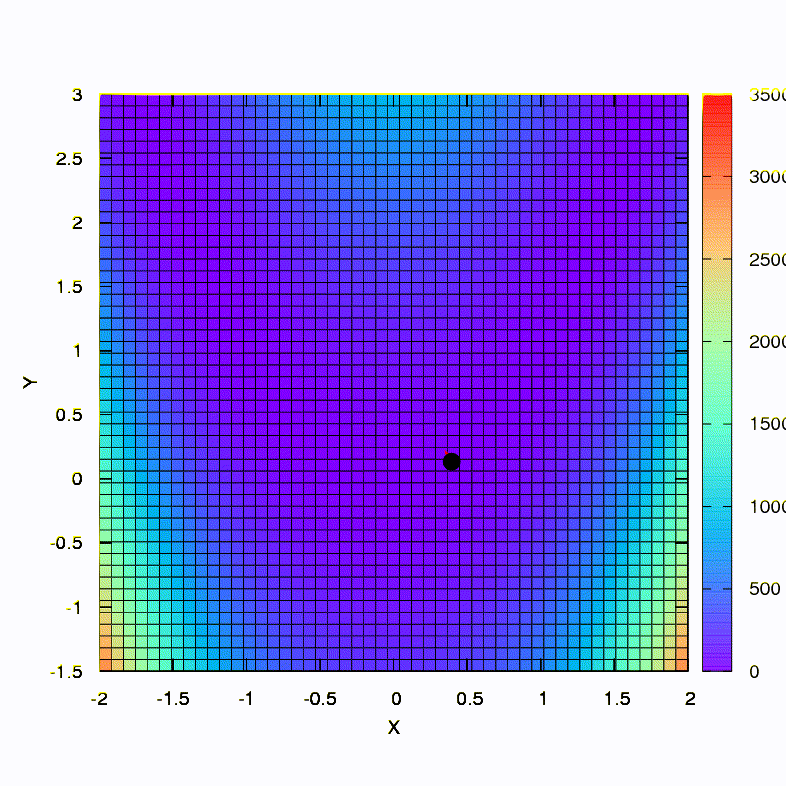
这就是下降方法在球形置信区域内的行为，它也是梯度下降。 一切都像一本教科书-我们陷入了峡谷。



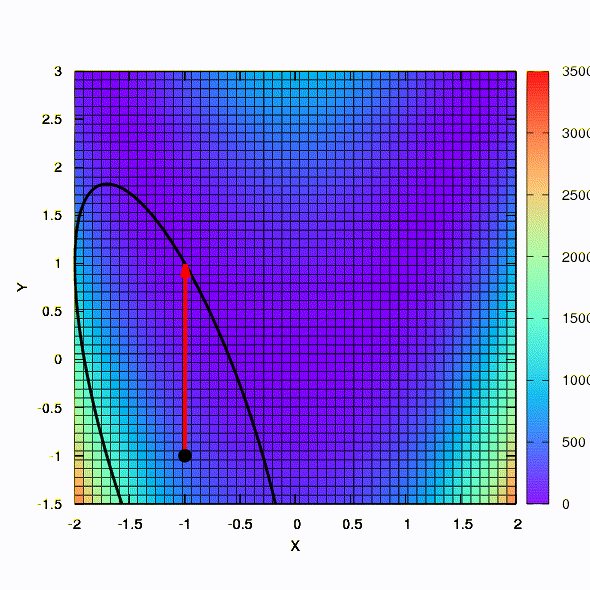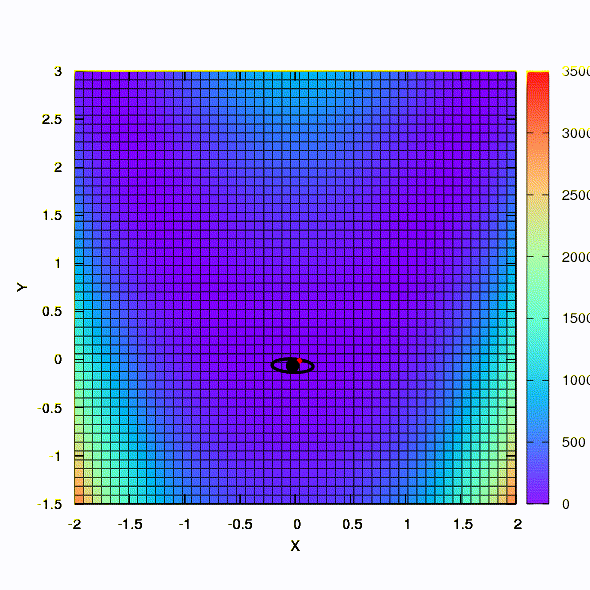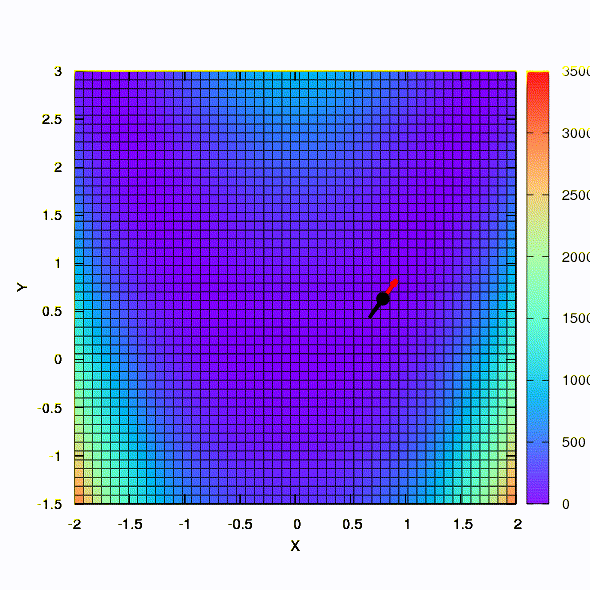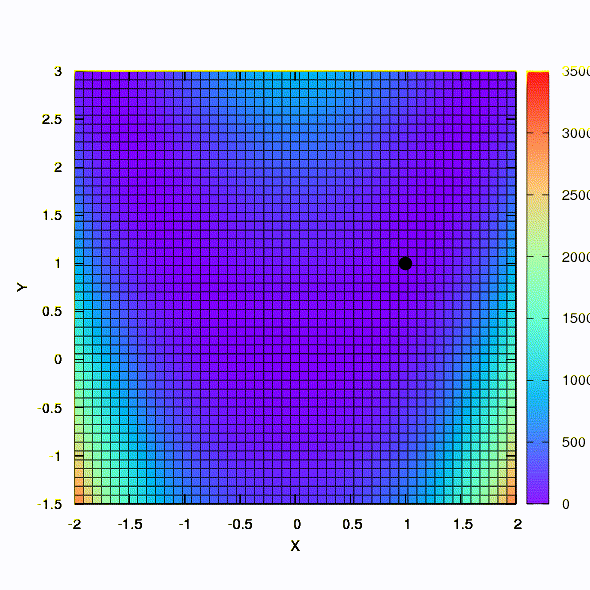
如果置信区域具有由Hessian矩阵定义的椭圆形状，则可以得到此结果。 这无非是阻尼牛顿法的迭代。

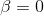
仅解决了如果Hessian矩阵不是正定的怎么办的问题。 有很多选择。 首先是得分。 也许您很幸运，如果没有此属性，牛顿的迭代将收敛。 这是很真实的，尤其是在最小化过程的最后阶段，当您已经足够接近解决方案时。 在这种情况下，可以使用标准牛顿法的迭代，而不必为寻找允许下降的邻域而烦恼。 或者在以下情况下使用阻尼牛顿法的迭代 即，在获得的方向不是下降方向的情况下，例如将其改变为反梯度。 只是不必根据Sylvester准则明确检查Hessian是否为正定 ，就象这里所做的一样！！！ 。 这是浪费和毫无意义的。
更细微的方法涉及在某种程度上接近于Hessian矩阵构造一个矩阵，但是具有正定性的特性，尤其是通过校正特征值。 另一个主题是拟牛顿法或可变度量方法，它们可以保证矩阵B的正定性，并且不需要计算二阶导数。 通常，对这些问题的详细讨论已经超出了本文的范围。

是的，顺便说一句，根据所说的， 具有Hessian正定性的牛顿阻尼法是一种梯度法 。 以及拟牛顿法。 还有许多其他选择，是基于方向和步长的单独选择。 因此，将牛顿法与梯度术语进行对比是不正确的。

总结一下

在讨论最小化方法时通常会记住的牛顿法通常不是经典意义上的牛顿法，而是具有由目标函数的黑森（Hessian）指定的度量的下降法。 是的，如果Hessian到处都是肯定的，它将在全球范围内收敛。 这仅对于凸函数是可行的，凸函数实际上在实践中要比我们想要的少得多，因此在一般情况下，如果没有适当的修改，牛顿方法的应用（我们不会脱离集合并继续称其为）不能保证正确的结果。 训练神经网络，甚至是浅层神经网络，通常会导致许多局部极小值出现非凸优化问题。 这是一次新的伏击。 牛顿法通常会快速收敛（如果收敛）。 我的意思是非常快。 奇怪的是，这很不好，因为我们在几次迭代中都达到了局部最小值。 对于具有复杂地形的功能，它可能比全局功能差很多。 线性搜索的梯度下降收敛速度要慢得多，但更有可能“跳过”目标函数的波峰，这在最小化的早期阶段非常重要。 如果您已经充分降低了目标函数的值，并且梯度下降的收敛速度显着降低，则此处度量的更改可能会加速该过程，但这是最后阶段。

当然，这种说法不是普遍的，也不是毫无争议的，在某些情况下甚至是不正确的。 以及关于梯度方法在学习问题中效果最好的说法。