Levenberg-Marquardt算法很简单。 Levenberg-Marquardt算法是有效的。
他们说他在梯度下降和牛顿法之间的中间位置,无论那是什么意思。 嗯,这是用牛顿的方法及其与梯度下降的联系来解决的。 但是,当他们说出这个深刻的短语时,它们是什么意思? 让我们尝试一下。
Levenberg同志在其文章中[K.一种解决最后平方中某些问题的方法。 夸脱。 应用 数学 1944年。 2. P. 164-168。],以及继他之后的公民Marquardt [Marquardt,Donald(1963)。 “非线性参数的最小二乘估计算法。” SIAM应用数学杂志。 11(2):431–441。]考虑了最小二乘问题,它看起来像这样:

,
可以用矢量形式更轻松地编写

。
而且,通过对最小二乘法进行完全评分,您甚至可以变得更加轻松。 这不会影响故事。
所以,这个问题被认为

。
这样的问题经常出现,以至于很难找到高效率的解决方法的重要性。 但是我们将从另一个开始。 在以前的文章中,已经表明,不仅可以通过以下考虑获得众所周知的梯度下降方法。 假设我们到了某个时候

其中最小化功能很重要

。 我们在这一点上定义一个辅助功能
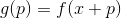
以及它的一些模型
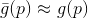
。 对于此模型,我们提出一个辅助问题

在哪里

-选择一定的预定允许值集合,以使问题具有简单的解决方案和功能
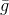
相当准确地近似

在

。 这种方案称为信任区域方法,很多

在其上最小化模型函数的值-此函数的置信区域。 对于梯度下降,我们采用

,对于牛顿法

,并作为

泰勒展开的线性部分
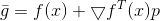
。
让我们看看如果我们通过使模型复杂化会发生什么
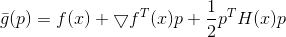
。
我们在椭圆置信区域上最小化此模型函数

(增加了乘数以方便计算)。 应用拉格朗日乘数法,我们得到了问题

,
其解决方案满足平等

或

在这里,与我们之前使用线性模型时看到的相反,方向
p 不仅取决于
度量 
,还取决于
信任区域的
大小 
,这意味着线性搜索技术不适用(至少合理地适用)。 事实也很难明确地确定该值

对应于

。 但是,显然,随着

长度

会减少。 但是,如果我们仍然施加条件
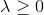
,则步长将不超过牛顿方法所给出的步长(全时兴,无需修改和条件)。
所以我们可以给定的

寻找正确的价值

,完全相反:找到这个
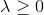
在这种情况下

。 在这种情况下,这是后期搜索的一种替代。 Marquardt提出了以下简单程序:
- 如果有一些价值
 条件
条件 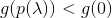 完成然后重复
完成然后重复  直到
直到 
- 如果
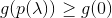 然后接受
然后接受 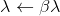 并重复。
并重复。
在这里

和

是作为方法参数的常量。 乘以

对应于置信区域的扩展,并乘以

-缩小。
指定的技术可以应用于
任何目标函数。 请注意,与早先考虑的情况相比,此处不再需要Hessian的正定性,而之前提出的牛顿法是顺序下降法的特殊情况。 甚至不需要其非简并性,这在某些情况下非常重要。 但是,在这种情况下,方向搜索的价格会增加,因为每次更改

导致需要解决线性系统来确定

。
让我们看看如果将这种方法应用于最小二乘问题,将会发生什么。
梯度函数
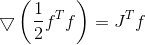
她的粗麻布
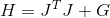
在哪里

。 替换并获得以下确定搜索方向的系统
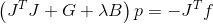
。
这是完全可以接受的,但是计算向量函数的二阶导数可能会非常昂贵。 Marquardt建议使用函数本身来绕过此问题。

,及其线性近似
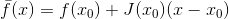
在矩阵

变为零。 如果现在作为

取单位矩阵
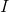
,则我们得到Levenberg-Marquardt方法的标准形式来解决最小二乘问题:

。
对于这种确定下降方向的方法,Marquardt证明了有抱负的定理

到无穷大方向

倾向于反梯度。 有兴趣的读者可以在基础文章中找到严格的证明,但是我希望从方法的逻辑上,这种陈述本身已经变得很明显。 在某种程度上,它证明了普遍存在的事实,即随着lambda的增加(由于某种原因我经常称其为正则化参数),我们得到了梯度下降。 实际上,没有任何东西-我们只会在极限内,步长趋于零的极限中得到它。 更重要的是,具有足够大的λ值,我们获得的
方向将是
下降方向 ,这意味着我们获得了
该方法的
全局收敛性 。 这是语句的第二部分,当lambda趋于零时,我们得到牛顿法,这显然是正确的,但前提是我们必须接受

它的线性近似
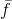
。
似乎全部。 我们在椭圆度量中最小化向量函数的范数-我们使用Levenberg-Marquardt。 我们正在处理一种通用形式的函数,并且具有计算二阶导数矩阵的能力-对于Wells,请使用通用区域置信区域方法。 但是有变态...
有时用Levenberg-Marquardt方法最小化功能

他们调用这样的表达式:

。
一切似乎都一样,但是在这里

-第二矩阵! 导数函数

。 形式上,这是存在的权利,但这是一种变态。 这就是为什么。 Marquardt在他的文章中提出了一种求解方程组的方法

通过最小化功能

所描述的方法。 如果作为
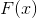
取目标函数的梯度,那么我们实际上得到了简化的表达式。 而变态是因为
解决了由极小化问题产生的非线性方程组产生的极小化问题 。
双重打击。 这样的表达式至少不比球形置信区域的第一个方程更好,但是从生产率(不必要的乘法运算,在正常的实现中是分解)的角度,以及从方法稳定性的角度(矩阵乘法本身会恶化),通常情况下,这种表达式要差得多。其条件)。 有时有人反对

保证肯定定义,但是在这种情况下没有关系。 让我们从顺序下降法的角度看一下Levenberg-Marquardt方法。 在这种情况下,事实证明我们要使用矩阵作为度量
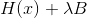
,这样她就可以以这种身份行事

应确保其积极确定性。 鉴于

正定值

总是可以找到的-因此无需要求

没有观察到肯定的确定性。
作为矩阵

不需要取一个单位,但是对于目标函数的二次模型,指定适当的置信区域不再像线性模型那样简单。 如果我们采用由Hessian诱导的椭圆区域,则该方法会退化为牛顿法(嗯,几乎)
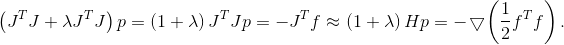
当然,除非Hessian矩阵是正定的。 如果不是,则可以像以前一样,使用校正后的Hessian作为度量标准,或使用某种程度上接近它的矩阵。 还建议使用矩阵作为度量
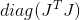
,通过构造保证它是正定的。 不幸的是,对于这种选择,我至少不知道有任何严格的理由,但是作为经验推荐经常提到。
作为说明,让我们看一下该方法在同一个Rosenbrock函数上的行为,我们将以两种形式来考虑它-作为形式简单的函数

,
作为最小二乘问题
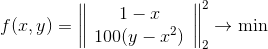

这就是具有球形置信度区域的方法的行为方式。
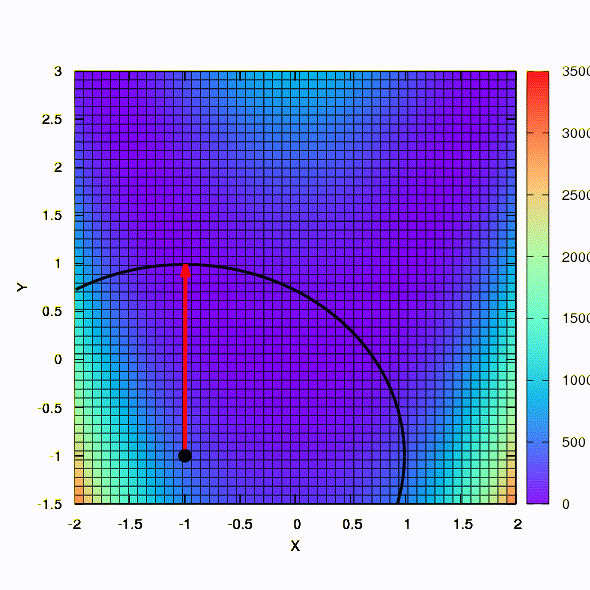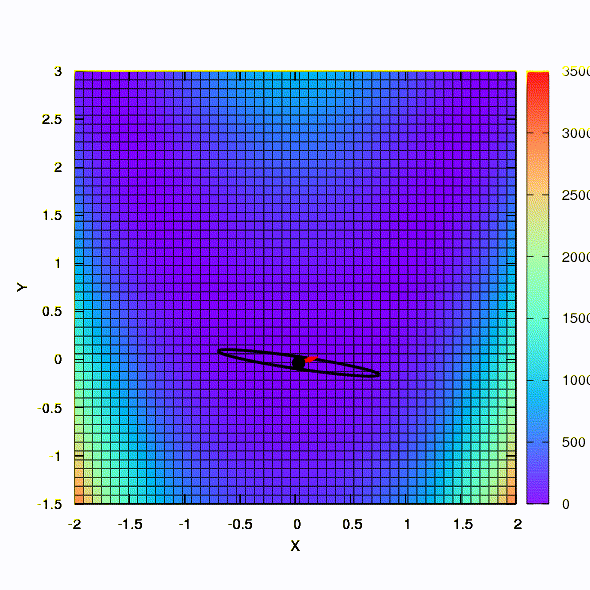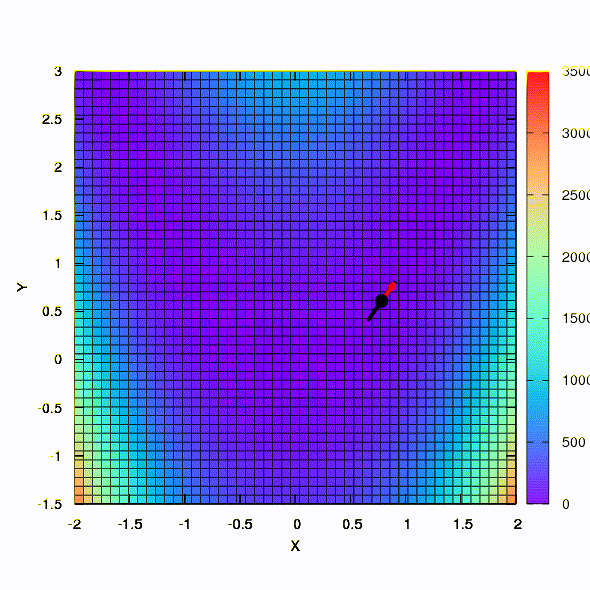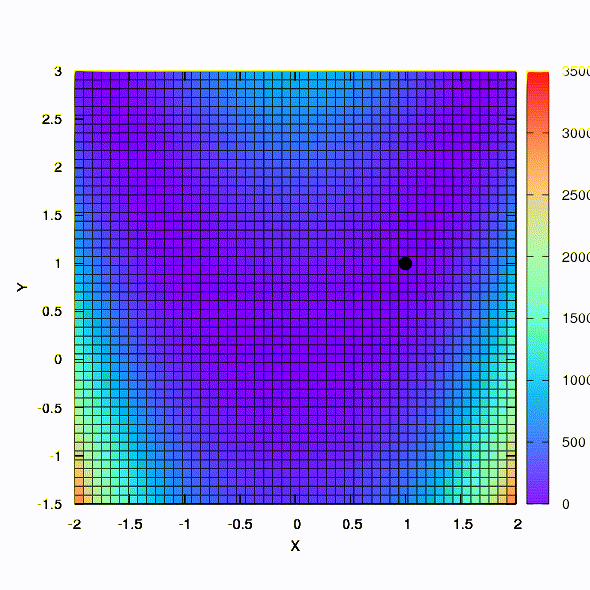
因此,如果置信区域的形状由根据Davidon-Fletcher-Powell规则构造的矩阵给出,则采用相同的方法。 对收敛有影响,但比使用目标函数的线性模型时的情况要适度得多。
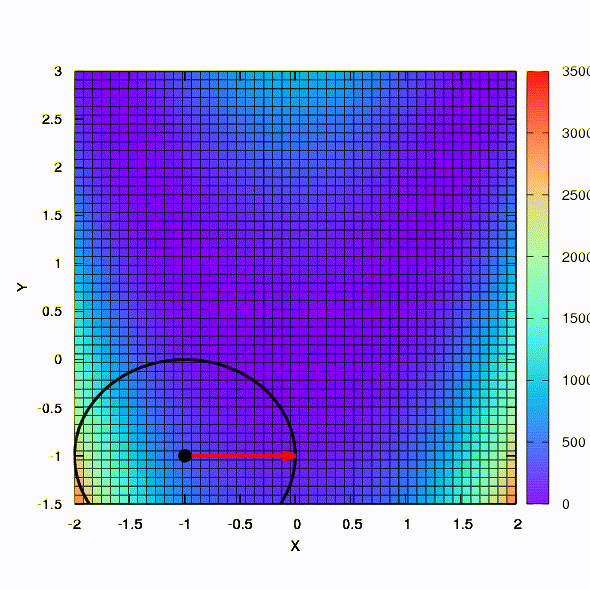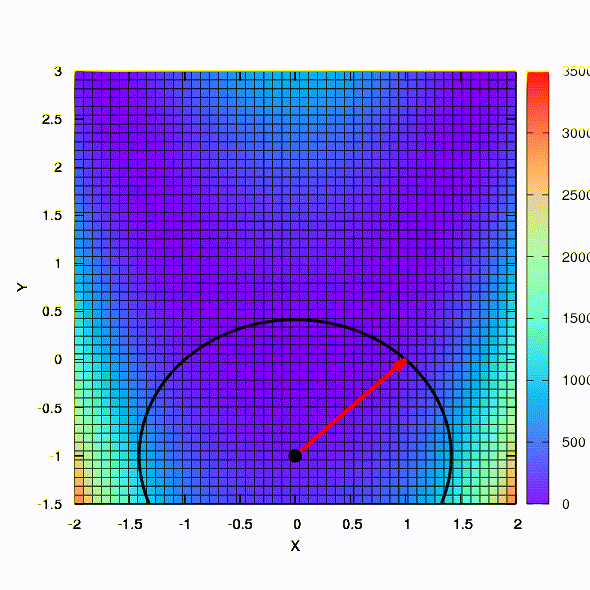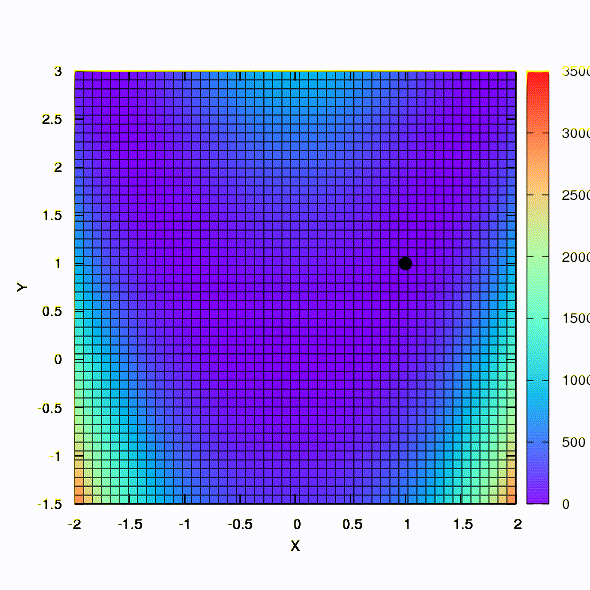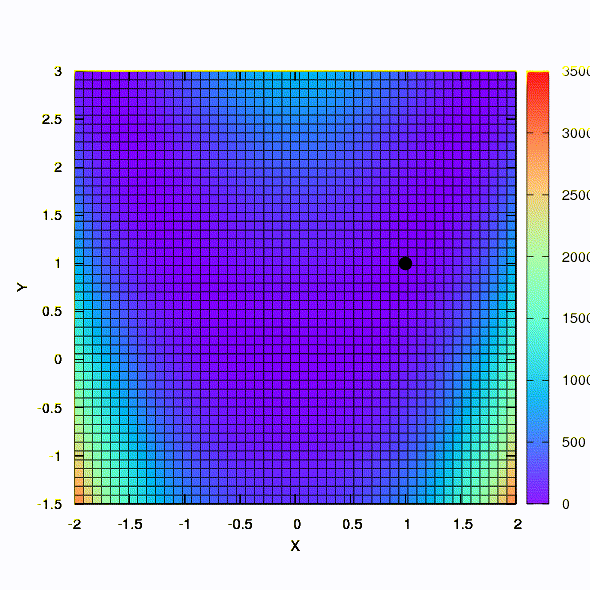
这就是应用于最小二乘问题的方法的行为。 它在5次迭代中收敛。 请
不要从这个结论中得出这样的功能的第二种说法总是比第一种更好 。 事实并非如此,这只是在这种特殊情况下发生的。
结论
据我所知,Levenberg-Marquardt方法是基于信任区域的思想的第一种方法。 在解决最小二乘问题时,他在实践中表现出色。 在大多数情况下(由我看到),该方法收敛很快(在上一篇文章中我说过是好是坏)。 但是,在最小化一般功能的同时,选择球体作为信任区域并不是最佳选择。 另外,该方法的一个显着缺点(在这里描述了其基本公式)是置信区域的大小是隐式设置的。 缺点是知道含义

我们当然可以在当前点计数

只计算步幅

。 但是,当我们移动到新的点时,相同的值

一个完全不同的置信区域值将已经对应。 因此,我们失去了确定置信区域“任务特征”大小的能力,并被迫在每个新点以新方式确定其大小。 当需要足够大量的迭代来收敛时,这可能很重要,并且计算函数的值很昂贵。 基于信任区域的思想,可以通过更高级的方法解决类似的问题。
但这是一个完全不同的故事。
加法
多亏了
Dark_Daiver的宝贵意见
,我决定在上面补充以下说明。 当然,可以通过另一种纯粹的经验方法得出Levenberg-Marquardt方法。 即,让我们回到上一篇文章中描述的顺序下降方法的方案,并再次问自己一个问题,即为目标函数的线性模型构造一个足够的度量。
假设搜索空间中当前点的Hessian矩阵不是正定的,并且不能用作度量(此外,要检查是否是如此,我们既没有能力也没有欲望)。 表示为
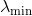
它的最小特征值。 然后我们可以通过简单地将其所有特征值偏移
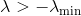
。 为此,只需将矩阵添加到黑森州
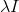
。 然后确定下降方向的方程将采用以下形式
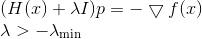
如果我们的分数较低
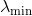
,那么我们就可以完成在顺序下降方法中完成的所有工作。 但是,如果我们没有这样的估计,那么考虑到

长度
p会减小,我们可以放心地说,有足够大的长度

同时

正定和

。
为什么我认为这种方法的结论不太成功。 首先,以这种方式构造的度量标准是否适合于实际使用一点也不明显。 当然,它使用有关二阶导数的信息,但是它不会随随便便地移动特征值一个给定值不会使其失效的任何地方。 正如同事在评论中指出的那样,很明显,在Hessian矩阵中添加缩放的恒等矩阵会导致以下事实,即椭圆置信区域将趋于球形,并且在这里(看来)再次出现了卡在峡谷中的问题以及其他梯度下降和接近下降的乐趣。给他方法。 但实际上这不会发生。 无论如何,我从来没有观察到过说明这种行为的例子。 在这种情况下,就会出现问题:
但是,实际上,为什么呢?
但是,如果我们不是将这种方法视为下降方法的特殊情况,而是将其视为具有目标函数二次模型的置信区域方法,就不会出现这样的问题,因为答案很明显:当λ增加时,我们只是压缩球体-模型的置信区域。 关于曲率的信息不会随处可见,也不会被任何东西冲走-我们只需要选择二次模型足以描述目标函数的区域大小即可。 由此可以得出结论,由于度量模型的变化已经考虑到了我们对目标函数的所有信息,因此很难期望度量标准的变化(即置信区域的形状)会产生显着影响。
其次,在考虑一种方法时,重要的是要理解使Marquardt引入该方法的主要思想,即信任区域的思想。 确实,归根结底,只有了解数值方法的来龙去脉才能使我们理解它为什么起作用,更重要的是,为什么它不起作用。