本文将讨论在最小化期限方面开发可创建有效债券投资组合的计划的经验。 也许我不会独树一帜，对于每个投资债券的人来说，确定最佳权重的问题早已得到解决，但我仍然希望所描述的方法和所提供的程序代码对某人有用。

由于其中包含少量数学，因此该文章对某人似乎很复杂。 但是，如果您已经决定开始投资，那么您需要为数学经常出现在金融现实中并且更加复杂的事实做好准备。

该程序的源代码和用于优化的示例产品组合可在GitHub上获得。

更新：按照承诺，提供了一个简单的Web服务，该程序使每个人都可以使用该程序，而无需复制或编译代码。
链接
在同一地方使用说明。
如果某些方法不起作用或您需要解决某些问题，请在注释中写下。

因此，我们的任务是形成有效的债券投资组合。

第1部分。确定投资组合的期限

从最小化非系统性风险（投资组合多样化）的角度出发，证券的选择是通过考虑特定发行人，发行人（如果不限于OFZ ），账面行为等参数来进行的。 （这种分析方法对于每个投资者而言都是非常个别的，因此本文中不予考虑）。

选择了几只最适合投资的证券后，一个自然的问题出现了：您需要购买每期债券多少张债券？ 这是优化投资组合以使投资组合的风险最小化的任务。

将持续时间视为优化参数是很自然的。 因此，任务是确定证券在证券中的权重，以使得对于某些固定的证券收益率，证券的持续时间将最小。 在这里您需要进行一些保留：

1. 债券投资组合的期限由其组成证券决定。 这些持续时间是已知的（它们是在公共领域中）。 投资组合期限不等于包含在其中的证券的最大期限（存在谬论）。 单个证券的久期与整个投资组合的久期之间的关系不是线性的，即 不等于其构成债券的加权平均期限（要验证这一点，只需考虑期限公式（请参阅下面的（1））并尝试计算有条件投资组合的加权平均期限，例如，由两篇论文组成。在每篇论文的输出中，我们得到的不是投资组合期限的公式，而是一种“废话”，具有两个折现率和不一致的现金流量作为权重。
2. 与持续时间不同，投资组合收益取决于线性投资工具的收益。 即 通过将钱放入固定收益的几种工具中，我们将获得与每种工具的投资额成正比的回报（这适用于复杂的汇率，而不仅仅是简单的汇率）。 确保这更加容易。
3. 到期收益率（ YTM ）用作债券的收益率。 通常用于计算持续时间。 但是，这里整个投资组合的到期收益率是相当随意的，因为 所有证券的到期日都不同。 形成投资组合时，必须从一定意义上考虑此功能，因为应该对投资组合进行审查，并且不得少于构成其的工具。

因此，第一个任务是正确计算投资组合本身的持续时间。 立即执行此操作的方法是： 确定投资组合的所有付款，计算到期收益率，折现付款，将收到的价值乘以这些付款的条件并相加。 为此，您需要将所有工具的付款日历合并到整个投资组合的单个付款日​​历中，组成一个表达式以计算到期收益率，对其进行计算，对每笔付款进行折现，再乘以到期日，加... 一般来说，一场噩梦。 即使对于两篇论文，要做到这一点也是一项艰巨的任务，更不用说将来定期重新计算投资组合了。 这种方式不适合我们。

因此，有必要寻找机会以另一种更快的方式确定投资组合的期限。 可接受的选项是允许您通过已知工具期限确定投资组合的期限。 对持续时间公式的研究表明存在这样一条路径，在此我想详细介绍一下（如果有人对计算的数学细节不感兴趣，则可以安全地跳过包含公式的几段内容，然后直接转到示例）。

债务工具的期限定义如下：

$$$$ display $$ \ begin {equation} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~（1）\结束{equation} $$显示$$

其中：

• _i是第i次付款的时间点；
• $$$ inline $ \开始{equation} PV_i = \ frac {CF_i} {（1 + r）^ {t_i}} \ end {equation} $ inline $ -第i次折扣付款；
• CF _i-第i次付款；
• r是折现率。

我们引入折现系数k =（1 + r），并考虑折现付款额P与k的关系 ：

$$$$显示$$ \开始{等式} P（k）= \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~ ~~~~（2）\ end {等} $$显示$$

相对于k微分P ，我们得到

$$$$ display $$ \开始{等式} P'（k）=-\ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} =-\ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~（3）\ end {equation} $$显示$$

在给定后者的情况下，债券期限的表达形式为

$$$$ display $$ \开始{等式} D = -k \ frac {P'（k）} {P（k）} ~~~~~~~~~~~~~（4）\结束{等式} $$显示$$

同时，我们记得在债券情况下，使用折现率r作为到期收益率（YTM）。

获得的表达式对一个债券有效，但我们对债券投资组合感兴趣。 让我们继续确定投资组合的期限。

我们引入以下符号：

• P _i是第i个债券的价格；
• z _i-投资组合中第i个债券的证券数量；
• k _i-投资组合中第i个债券的折现系数；
• $$$ inline $ \开始{equation} P_p = \ sum_ {i} {z_iP_i} \ end {equation} $ inline $ -投资组合价格；
• $$$ inline $ \开始{equation} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {equation} $ inline $ -投资组合中第i个债券的权重； 明显的要求$$ $ inline $ \开始{equation} \ sum_ {i} w_i = 1 \ end {equation} $ inline $ ;
• $$$ inline $ \开始{equation} k_p = \ sum_ {i} w_ik_i \ end {equation} $ inline $ -投资组合折现系数；

由于微分的线性关系，因此以下是正确的：

$$$$显示$$ \开始{等式} P'_p（k）= \左（\ sum_ {i} z_iP_i（k）\右）'= \ sum_ {i} z_iP'_i（k）~~~~~ ~~~~~~~~（5）\ end {equation} $$ display $$

因此，考虑到（4）和（5），投资组合的持续时间可以表示为

$$$$ display $$ \ begin {equation} D_p = -k_p \ frac {P'_p} {P_p} =-\ sum_ {i} w_ik_i \ left（\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ right）~~~~~~~~~~~~~~（6）\ end {equation} $$ display $$

从（4）可以清楚地得出$$ $ inline $ \开始{equation} P'_j =-\ frac {D_jP_j} {k_j} \ end {equation} $ inline $ 。
将表达式替换为（6），我们得出投资组合期限的以下公式：

$$$$ display $$ \ begin {equation} D_p = \ sum_ {i} w_ik_i \ left（\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ right） = \左（\ sum_ {i} w_ik_i \右）\左（\ sum_ {j} w_j \ frac {D_j} {k_j} \右）~~~~~~~~~~~~~（7）\结束{equation} $$显示$$

在已知每种工具的期限和到期收益率的条件下（我们记得，我们正处于这样的条件下），表达式（7）是根据其债券期限确定投资组合期限的理想公式。 它看起来似乎很复杂，但是实际上，借助MS Excel最简单的功能，它已经可以实际使用了，我们现在将通过一个示例来做。

例子

为了根据公式（7）计算投资组合的期限，我们需要输入数据，其中包括投资组合中包含的证券的实际集合，其期限和到期收益率。 如上所述，该信息是公开可用的，例如，在债券分析部分的网站rusbonds.ru上。 源数据可以Excel格式下载。

例如，考虑由9个债券组成的证券投资组合。 从rusbonds下载的原始数据表具有以下格式。



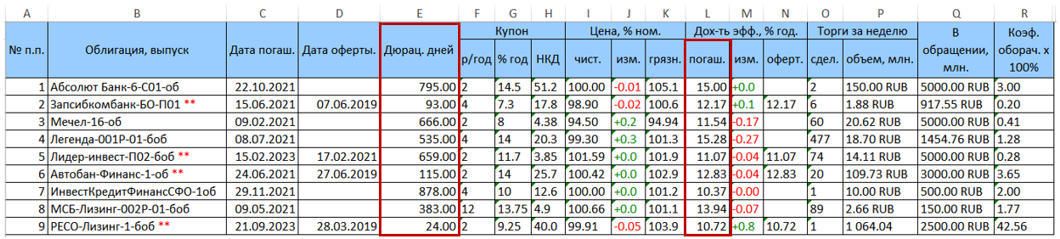
我们感兴趣的两列持续时间（E列）和到期收益率（L = YTM列）以红色突出显示。

我们为该投资组合中的债券设置权重w（到目前为止，可以通过任意方式，但是它们的总和等于1），并计算k =（1 + YTM / 100）和D / k =（“列E” / k）。 转换后的表（没有多余的列）看起来像



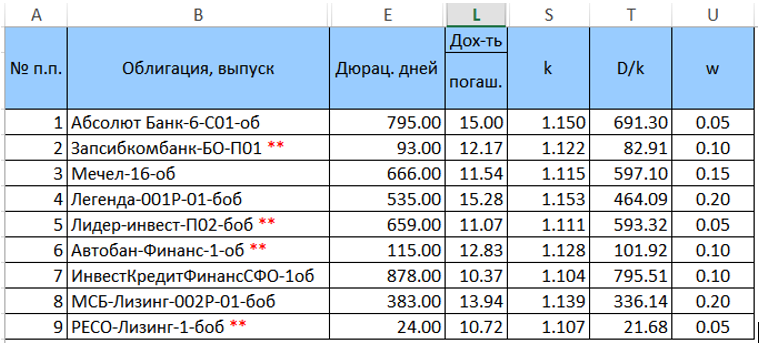
接下来，我们计算乘积$$ $ inline $ \开始{equation} w_j \ frac {D_j} {k_j} \ end {equation} $ inline $ 和$$ $ inline $ \开始{equation} w_ik_i \ end {equation} $ inline $ 并将它们相加，然后将结果乘以另一个。 乘法的结果将是给定权重分布所需的持续时间。



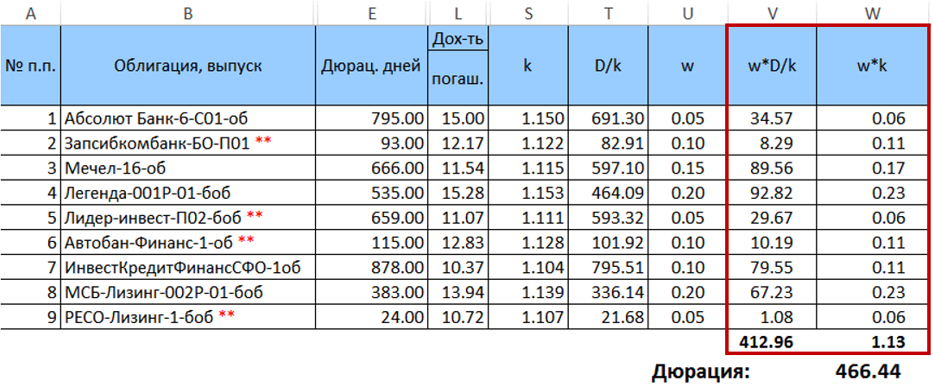
因此，投资组合的期望期限为466.44天。 重要的是要注意，在这种特殊情况下，公式（7）计算的持续时间与相同权重（偏差<0.5天）计算出的加权平均持续时间略有不同。 但是，这种差异随着权重分布的增加而增加。 随着纸张持续时间分布的增加，它也会增加。

在获得用于计算投资组合期限的公式之后，下一步是确定证券的权重，以便在给定收益率下，投资组合的估计期限将最小。 我们进入下一部分-投资组合优化。

第2部分。债券投资组合优化

表达式（7）是二次形式，矩阵

$$$$ display $$ \开始{equation} A = \左\ {k_i \ frac {D_j} {k_j} \ right \} = \开始{pmatrix} D_1＆\ ldots＆k_1 \ frac {D_n} {k_n} \ \ \ vdots＆D_j＆\ vdots \\ k_n \ frac {D_1} {k_1}＆\ ldots＆D_n \ end {pmatrix} \ end {equation} $$显示$$

因此，以矩阵形式，投资组合（7）的持续时间的表达式可以写成如下：

$$$$ display $$ \开始{equation} D_p = w ^ TAw ~~~~~~~~~~~~~~（8）\ end {equation} $$ display $$

其中w是投资组合中债券权重的列向量。 如上所述，向量w的元素之和必须等于1。 另一方面，表达 $$$k_p = \ sum_ {i} w_i k_i$ （本质上是简单的标量积（ w ， k ，其中k是债券贴现系数的向量））应等于投资组合的目标贴现率，因此应设定目标投资组合收益率。

因此，优化债券投资组合的任务是使具有线性约束的二次函数（8）最小化。

查找多个变量的条件极值的经典方法是拉格朗日乘数法。 但是，此方法仅在矩阵A因构造而退化时才适用（此处不仅如此;我们在此省略了拉格朗日方法的适用性分析的详细信息，以免过多的数学内容使文章不繁琐）。

无法使用简单且负担得起的分析方法导致需要使用数值方法。 优化二次函数的问题是众所周知的，并已在公共图书馆中实施了几种长期发展的高效算法。

为了解决这个特定问题，使用了minGLp软件包中包含的ALGLIB库和其中实现的二次优化算法QP-Solvers 。

一般而言，二次优化问题如下：

需要找到一个使函数最小的n维向量

$$$$ display $$ \开始{等式} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~~（9）\结束{等式} $$显示$$

在给定限制下
1） l≤w≤u ;
2） Cw * d ;
其中w，l，u，d，b是n维实值向量， Q是二次部分的对称矩阵，并且符号*表示≥=≤的任何关系。
从（8）可以看出，我们目标函数中的线性部分b ^T w等于零。 然而，矩阵A不是对称的，然而，这不防止在不改变函数本身的情况下使其成为对称形式。 为此，只需将表达式代替A$$ $ inline $ \开始{equation} \ frac {A ^ T + A} {2} \ end {equation} $ inline $ 。由于公式（9）包含系数 $$$\ frac {1} {2}$ 那么我们作为Q我们可以接受 $$$A ^ T + A$ 。

向量l和u的坐标指定了所需向量的边界，并且在[-1,1]范围内。 由于我们不假定卖空债券，因此在我们的情况下，向量的坐标都不少于0。在下面的示例程序中，为简单起见，假设向量l为零，向量u的系数均为 0.3 。 但是，没有什么可以阻止我们改进程序并使约束向量更可定制。

在我们的案例中，矩阵C由两行组成：1）折现系数，当将其标量乘以权重（相同（ w ， k ））时，应给出投资组合的目标收益率； 2）由单位组成的字符串。 需要设置限制 $$$\ sum_ {i} w_i = 1$ 。

因此，用于我们任务的表达式Cw * d看起来像这样：

$$$$ display $$ \开始{等式} \左\ {\开始{array} {ccc}（{\ bf w，k}）= k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \对。 ~~~~~~~~~~~~~~（10）\ end {equation} $$ display $$

现在，我们转向搜索最佳投资组合的软件实现。 对象中的ALGLIB二次优化器的基础 $$$\ tt \ smallminqpstate$

alglib::minqpstate state; 

为了初始化优化器，该对象与任务维度参数n一起传递给minqpcreate函数。

 alglib::minqpcreate(n, state); 

接下来最重要的一点是选择优化算法（求解器）。 用于二次优化的ALGLIB库提供了三个求解器：

• QP-BLEIC是最通用的算法，旨在解决线性约束数量（形式为Cw * d ）不是很大（根据文档的建议最多为50）的问题。 同时，它可以在大尺寸任务上有效（如文档所述-最多n = 10000）。
• QuickQP是一种非常有效的算法，尤其是在优化凸函数时。 但是，不幸的是，它不能用于线性约束-仅适用于边界条件（形式为l≤w≤u ）。
• Dense-AUL-针对超大尺寸和大量限制的情况进行了优化。 但是，根据文档，使用其他算法将可以更有效地解决小尺寸任务和限制数量的问题。

鉴于以上特征，很明显，QP-BLEIC求解器最适合我们的任务。

为了指示优化器使用此算法，必须调用该函数 $$$\ tt \ small minqpsetalgobleic$ 。 对象本身和停止条件将传递给此函数，在此我们将不对其进行详细介绍：在此处考虑的程序中，将使用默认值。 函数调用如下：

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

求解器的进一步初始化包括：

• 二次部分的矩阵的转移Q- $$$\ tt \ small alglib :: minqpsetquadraticterm（state，qpma）;$
• 线性部分的矢量（在本例中为零矢量）的传输- $$$\ tt \ small alglib :: minqpsetlinearterm（state，b）;$
• 边界条件向量l和u-的传递 $$$\ tt \ small alglib :: minqpsetbc（state，bndl，bndu）;$
• 线性传动- $$$\ tt \ small alglib :: minqpsetlc（state，c，ct）;$
• 设置向量空间的坐标比例 $$$\ tt \ small alglib :: minqpsetscale（state，s）;$

让我们来谈谈每个项目：
为了指定向量和矩阵，ALGLIB库使用特殊类型的对象（整数和实值）： $$$\ tt \ small alglib ::整数\ _1d \ _array$ ， $$$\ tt \ small alglib ::实\ _1d \ _array$ ， $$$\ tt \ small alglib ::整数\ _2d \ _array$ ， $$$\ tt \ small alglib ::真实\ _2d \ _array$ 。 要准备矩阵，我们需要一个类型 $$$\ tt \ small real \ _2d \ _array$ 。 在程序中，首先创建一个矩阵A （ $$$\ tt \ small alglib ::实数\ _2d \ _array〜qpma$ ），然后根据公式 $$ 从中我们构造出矩阵Q （ $$$\ tt \ small alglib ::实数\ _2d \ _array〜qpmq$ ） 在ALGLIB中设置矩阵尺寸是一项单独的功能 $$$\ tt \小设定长度（n，m）$ 。

要构造矩阵，我们需要折现系数（ k _i ）的向量以及持续时间与这些系数的关系（ $$$\ frac {D_j} {k_j}$ ）：

 std::vector<float> disfactor; std::vector<float> durperytm; 

下面的清单中显示了实现矩阵构造的代码片段：

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

如前所述，线性部分的向量在我们的情况下为零，因此一切都很简单：

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

向量边界条件通过一个函数传输。 为了解决这个问题，应用了非常简单的边界条件：每张纸的重量不应该小于零（我们不允许负位置）并且不应该超过30％。 如果需要，限制可能会很复杂。 使用该程序进行的实验表明，即使在此范围内进行简单的更改也会极大地影响结果。 因此，下限的增加和/或上限的减少导致最终投资组合的分散化，因为在优化过程中，求解器可能会将某些证券从所得向量中排除（将其权重分配为0％），这是不合适的。 如果将比例的下限设置为5％，则可以保证所有论文都包含在投资组合中。 但是，在这种设置下计算出的持续时间当然会比优化器可以排除纸张的情况下更长。

因此，边界条件由两个向量设置并转移到求解器：

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

接下来，优化器需要传递系统指定的线性约束（10）。 在ALGLIB中，这是使用函数完成的 $$$\ tt \ small alglib :: minqpsetlc（state，c，ct）$ ，其中c是结合系统（10）左侧和右侧的矩阵，即 视图矩阵 $$$（C ~~ d）$ ，ct是关系的向量（即≥，=或≤形式的对应关系）。 在我们的情况下，ct =（0,0），它对应于系统（10）两行的比率'='。

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

ALGLIB库的文档强烈建议在启动优化器之前设置变量的比例。 如果变量以单位计量，其变化相差一个数量级，则这一点尤其重要（例如，在寻找解决方案时，吨可以以百分之一或千的形式更改，单位可以是米;可以在吨米的空间中解决问题），这会影响放弃的标准。 但是，有一个保留意见，即在变量的缩放比例相同的情况下，不必设置缩放比例。 在所考虑的程序中，为了更严格地执行该方法，我们仍然执行规模任务，特别是因为它非常容易执行。

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

接下来，我们将优化器设置为起点。 通常，此步骤也是可选的，并且程序无需明确定义起点即可成功完成任务。 同样，出于严格的原因，我们设置了起点。 我们不会很聪明：起点将是所有债券权重相同的点。

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

剩下的就是确定优化器将返回找到的解决方案的变量和状态变量。 然后，您可以运行优化并处理结果

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

特别是，该程序的运行时并未在实验中进行衡量，但是一切运行得非常快。 同时，很明显，私人投资者不太可能优化超过10-15只债券的投资组合。

注意以下几点也很重要。 优化器精确地返回权重向量。 要获得计算的持续时间本身，您必须直接使用公式（8）。 该程序可以做到这一点。 为此，专门增加了两个向量和矩阵相乘的功能。 我们不会在这里给他们。 希望自己的人可以在已发布的源代码中轻松找到它们。

仅此而已。 对所有人的债务工具进行有效投资。

PS理解选择别人的代码并不是最有吸引力的职业，对于许多想要投资的人来说，它根本不是专门的，我稍后将尝试将该程序转变为每个人都可以使用的简单网络服务，无论数学知识如何和编程。