 我博客中的原始翻译比赛网站
我博客中的原始翻译比赛网站让我们向读者解释“规则30”的含义-这是一个基本的细胞自动机(请参阅Wiki ),其在二进制数系统中的状态(基于旧细胞构建新细胞水平的规则)设置为0-0-0-1-1-1。 -1-0,可以用十进制表示法解释为30。
那一切从哪里开始呢? -“规则30”
令人难以置信的简单事物怎么会
产生令人难以置信的复杂事物 ? 自从我
第一次熟悉规则30以来已经快40年
了,但是它仍然让我感到惊讶和高兴。 长期以来,它成为我在
科学史上个人最喜欢的发现
,多年来,它改变了我的整个世界观,并使我对
科学,技术,哲学等有了多种新型理解 。
但是即使经过了这么多年,我们仍然无法获得关于规则30的许多基本概念。 因此,我认为是时候应该采取一切可能的措施,以刺激确定这些基本模式的基本集合的过程。
因此,今天我向申请人提供30,000美元的总奖金,用于回答有关规则30的三个主要问题。
规则30非常简单:
有一系列黑白单元格(单元格)的序列,给定特定的黑白单元格行,确定下面一行中的单元格的颜色,分别查看每个单元格及其相邻的相邻单元格,然后将以下简单替换规则应用于它们,即:

代号RulePlot[CellularAutomaton[30]]
[观看视频,该视频在几分钟内讲述了细胞自动机和规则30的本质-译者注]
如果从一个黑格开始,会发生什么? [取一
排白色单元格,两边无限,一个黑色单元格,然后将上面显示的规则应用于该行,获得一个新行,等等-译者注 ]假设(我本人起初是这样做的)规则非常简单,并且根据其工作获得的模板也应相应地简单。 但是,如果您进行实验,您将看到算法的前50个步骤之后会发生什么:

代号RulePlot[CellularAutomaton[30], {{1}, 0}, 50, Mesh -> All,
ImageSize -> Full]
自然地,我们可以假设,由于该算法,将获得简单得多的数学对象。 但是,这是前300个步骤之后发生的情况:

这表明
在金字塔的左侧有一定的
图案 。 但是与此同时,此模板的许多方面
看起来都是随机形成的 。
如此简单的规则最终会导致如此复杂的系统行为,这是不可理解的。 基于此,我得出的结论
是,在所有可能的计算机程序
的计算领域中 ,这种行为非常普遍,甚至在几乎所有地方都如此。
基于这种假设,我根据观察简单算法操作的
原理,开发了一种形成
全新科学
类型的方法 。
逐渐地,越来越多的证据积累了这些原则。
但是,让我们回到规则30,详细考虑它允许我们做什么,以及它的用途是什么? 关于该算法的行为到底能说什么? 显而易见的是,即使是最明显问题的答案也很困难。
即使经过几十年没有找到答案,我仍然决定是时候问一些有关规则30的具体问题,同时用大量现金奖励来刺激这一领域。
我已经在2007年尝试做类似的事情,为回答有关特定
Turing机器的基本问题而
设立了奖项 。 在这种情况下,结果是肯定的,并且不需要很长时间即可等待。 仅仅几个月后,这个
奖项就获得了 -永久地确定了最简单的通用图灵机是什么,并且非常有说服力地证明了我先前开发
的计算等效性的一般
原理 。
规则30竞赛再次为解决关键任务设定了目标,即:
规则30的行为有多复杂 ? 每个任务都以其自己的方式,特别是在这个领域提出了一个问题。 与规则30本身一样,它们在原始设置上都看似简单。 尽管如此,对它们中的任何一个的解决方案都将是一项巨大的成就,最终将有助于阐明计算宇宙形成特性的基本原理,而这些基本原理远远超出了规则30的规定。
我
从事这些问题的工作已超过35年 。 一直以来,我一直试图在一致的数学或计算思维框架内找到正确的想法,目的是最终解决这些问题中的至少一个。 现在,我想向整个世界社区开放这一过程。 但是,我很想知道在解决这些问题上可以实现什么以及在这种情况下可以使用什么方法。
规则30-要解决的任务
对于规则30下的竞争任务,我优先考虑规则30算法的关键特征之一,即:
中心列单元格形成的
明显随机性 。 从一个黑色单元格开始,然后查看此列中单元格的颜色值顺序,您将得出结论,它们是随机的:

代号ArrayPlot[
MapIndexed[If[#2[[2]] != 21, # /. {0 -> 0.2, 1 -> .6}, #] &,
CellularAutomaton[30, {{1}, 0}, 20], {2}], Mesh -> All]
但是它们在什么意义上是
“真正随机的”呢? 并可以证明这一假设吗? 在竞赛框架内设置的每个任务都使用其自己的随机性标准,然后根据该标准询问序列是否是随机的。
任务1:中央列是否始终保持非周期性?
考虑规则30中心栏的开头:

代号ArrayPlot[List@CellularAutomaton[30, {{1}, 0}, {80, {{0}}}],
Mesh -> True, ImageSize -> Full]
不难发现此列中的值没有重复-这不是周期性的。 但是挑战是,中心柱会根本变成周期性的吗? 通过启动规则30,我们看到该序列即使
在前十亿步中也不会变为周期性。 为了确定并证明这一点需要做什么。
这是此序列的
前一百万个和
前十亿个值所在的链接(
Wolfram数据仓库 )。
任务2:中心列中单元格的每种颜色(黑色或白色)是否平均相等?
这是我们在Rule 30算法的中心列中按更多步骤依次计算黑白单元的数量时所得到的:

代号Dataset[{{1, 1, 0, ""}, {10, 7, 3, 2.3333333333333335}, {100, 52, 48, 1.0833333333333333},
{1000, 481, 519, 0.9267822736030829}, {10000, 5032, 4968, 1.0128824476650564},
{100000, 50098, 49902, 1.0039276982886458}, {1000000, 500768, 499232,
1.003076725850907}, {10000000, 5002220, 4997780, 1.0008883944471345},
{100000000, 50009976, 49990024, 1.000399119632349},
{1000000000, 500025038, 499974962, 1.0001001570154626}}]
对于黑白电池,结果肯定接近相等。 这里有问题的(问题的问题)是以下问题:
该关系是否随着循环中步数的增加而收敛到1 。
任务3:计算中心列的第n个单元格是否至少需要O( n )个运算?
要在中心列中找到第
n个单元格,您始终可以简单地将规则30运行
n步,计算下图中所选菱形内所有单元格的值:

代号With[{n = 100},
ArrayPlot[
MapIndexed[If[Total[Abs[#2 - n/2 - 1]] <= n/2, #, #/4] &,
CellularAutomaton[30, CenterArray[{1}, n + 1], n], {2}]]]
但是,如果直接这样做,它将
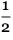 n 2个
n 2个单独的单元更新,因此,所需的计算能力随着O(
n 2 )的增加而增加。 这个问题的问题是,
是否有一种(而不是最快的)方法来计算第n个像元的值,而无需进行所有中间计算,或者尤其是少于O( n )个运算 。
组成Pi的数字
规则30是计算领域的产物:这是一个基于对可能的简单程序的研究的系统,该程序具有新的智能结构,由计算范式提供。 但是
,我在竞赛30中定义的任务具有数学上的类似物,这已经存在了多个世纪了 。
考虑
数字Pi中的数字值 。 这些数字的行为类似于规则30算法中心栏中的数据生成,也就是说,有一个给定的算法可以计算它们,一旦公式化,它们对于任何任务似乎几乎都是随机的。
![N [Pi,85] N [Pi,85]](https://habrastorage.org/getpro/habr/post_images/49e/ae6/17d/49eae617de3c0c9a864d4624413c6ce8.png)
只是为了使模拟更接近一点,这是Pi以2为底的数字系统中的前几位:
![BaseForm [N [Pi,25],2] BaseForm [N [Pi,25],2]](https://habrastorage.org/getpro/habr/post_images/18e/d4b/8f6/18ed4b8f6fd778443cc62470ea0956a9.png)
以下是规则30中心栏中的前几位:
![行[CellularAutomaton [30,{{1},0},{90,{{0}}}] 行[CellularAutomaton [30,{{1},0},{90,{{0}}}]](https://habrastorage.org/getpro/habr/post_images/9e9/f64/a52/9e9f64a521480621d3adbb859609742a.png)
代号Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]
为了好玩,您可以将它们转换为十进制:
![N [FromDigits [{Flatten [CellularAutomaton [30,{{1},0},{500,{0}}]],0},2],85] N [FromDigits [{Flatten [CellularAutomaton [30,{{1},0},{500,{0}}]],0},2],85]](https://habrastorage.org/getpro/habr/post_images/0df/d67/782/0dfd677828ca278c971d267948d88ad3.png)
代号N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]],
0}, 2], 85]
当然,众所周知,用于计算Pi的数字的算法比在规则30中心列中生成单元格的相对简单的规则要复杂得多。那么,我们对Pi的数字了解多少?
首先,我们知道它们不会重复。 这可以追溯到18世纪60年代,当时证明
Pi是一个非理性数 ,因为唯一重复的数字是有理数。 (在
1882年,还
证明Pi是先验的 ,也就是说,它不能通过多项式的根表示)。
那么问题2的表达可以得出什么样的类比? 我们是否知道在
Pi的一个数字序列中,以相同的频率出现不同的数字? 迄今为止
,已经计算出超过
100万亿个二进制数字 -并且所测量的数字频率非常接近(在
Pi的前
40万亿个二进制数字中 ,“单位与零”
之比约为0.99999998064)。 但是在计算极限时,频率会完全相同吗? 几个世纪以来,科学家一直在问这个问题,但是到目前为止,数学还没有给出答案。
对于有理数,由它们组成的数字序列是周期性的,并且很容易确定这些数字在数字中出现的相对频率。 但是,对于所有其他“自然创建的(自然构造的)”数字的数字序列,在大多数情况下,实际上几乎不知道该数字所包含的数字频率趋向于什么。 逻辑上假设Pi的数字(以及规则30的中心列)实际上是“
正常的 ”,这意味着不仅每个单独的数字,而且给定长度的任何数字块都以相等的最大频率相遇。 而且,正如在1930年代有关此主题的作品中所指出的那样,很有可能“构建正常数字的数字结构(模型)”。 通过合并连续整数的数字获得
的樟脑常数是上述推理的一个示例(可以通过合并连续整数的函数值在任何正常数的基础上获得相同的值):
![N [ChampernowneNumber [10],85] N [ChampernowneNumber [10],85]](https://habrastorage.org/getpro/habr/post_images/253/f93/8f3/253f938f3261e70f8985a49bf1158dde.png)
代号N[ChampernowneNumber[10], 85]
应当指出,这里的要点是,对于由标准数学函数的组合形成的“自然构造”的数字,找不到一个发现的示例,在该示例中将找到任何规则的数字序列。 自然,最后,此规定取决于“规律性”的含义,并且在某些阶段,任务变成了一种对
数位模拟的外星情报搜索 。 但是,没有证据表明不可能找到例如具有一系列具有明显规律性的数字序列的平方根的复杂组合。
那么,最后考虑Pi的问题3的类似物吗? 与规则30(一次计算一个序列中的元素的明显方法一次只一步)不同,传统的计算Pi位数的方法包括获得与Pi最佳近似的精确数字。 随着
Ramanujan在1910年发明并由1989年
Chudnovsky兄弟改进的标准(“ bizarre”)系列,该系列的前几个成员给出了以下近似值:

代号Style[Table[N[(12*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(k\)]*\(\((6*k)\)!\)*\((13591409 +
545140134*k)\)\), \(\(\((3*k)\)!\)
\*SuperscriptBox[\((\(k!\))\), \(3\)]*
\*SuperscriptBox[\(640320\), \(3*k + 3/2\)]\)]\))^-1, 100], {n, 10}] //
Column, 9]
那么,要找到第
n个数字,需要进行多少次运算? 该行中所需的项数为O(
n )。 但是每个条件都必须以
n位精度计算,这至少需要O(
n )个单独的计算操作,这意味着一般而言,计算工作量将大于O(
n )。
直到1990年代,人们一直认为没有计算所有先前的数字就无法计算Pi的
第n位数字。 但是在1995年,
西蒙·普拉夫 (
Simon Pluff)发现,尽管有一定的可能性,实际上可以计算出
第n个数字而无需计算前一个数字。 尽管人们会认为这将使您能够以少于O(
n )个运算获得第
n位数字,但是您需要以
n位数字的精度执行计算这一事实意味着至少
O( n )操作。
结果,类比和直觉
任务1:中央列是否始终保持非周期性?
在Rule 30竞赛的三项大奖中,这是解决该问题的大部分进展。 由于尚不知道规则30的中心列是否会变为周期性,因此
埃里卡·詹 (
Erica Jen)在1986年指出,没有两个列可以是周期性的。 而且实际上是这样,并且人们还可以支持
这样一个事实
,即一列与另一列中的单个单元格组合不能是周期性的 。
一对列的证明使用规则30的功能。考虑规则的结构:
![RulePlot [CellularAutomaton [30]] RulePlot [CellularAutomaton [30]]](https://habrastorage.org/getpro/habr/post_images/5fa/ca7/858/5faca785893d90e7969ef2a4dad73c58.png)
代号RulePlot[CellularAutomaton[30]]
可以简单地说,对于每个三元单元格,该规则由它确定中心单元格的颜色,但是对于规则30,您也可以有效地在侧面执行该规则:考虑到右侧和上方的单元格,您还可以唯一地确定左侧单元格的颜色。 这意味着,如果采用两个相邻的列,则
可以恢复左侧的整个模板 :

代号GraphicsRow[
ArrayPlot[#, PlotRange -> 1, Mesh -> All, PlotRange -> 1,
Background -> LightGray,
ImageSize -> {Automatic, 80}] & /@ (PadLeft[#, {Length[#], 10},
10] & /@
Module[{data = {{0, 1}, {1, 1}, {0, 0}, {0, 1}, {1, 1}, {1,
0}, {0, 1}, {1, 10}}},
Flatten[{{data},
Table[Join[
Table[Module[{p, q = data[[n, 1]], r = data[[n, 2]],
s = data[[n + 1, 1]] },
p = Mod[-q - r - qr + s, 2];
PrependTo[data[[n]], p]], {n, 1, Length[data] - i}],
PrependTo[data[[-#]], 10] & /@ Reverse[Range[i]]], {i, 7}]},
1]])]
但是,如果列具有周期性结构,则将立即恢复,还原的模板也应该是周期性的。 因此,例如,通过构造,至少初始条件绝对不是周期性的,因此两个列都不是周期性的。 如果各列不相邻,并且两列中的所有单元都不知道,则相同的语句为true。 但是,尚无将这种规定分配给单个列(例如中央列)的方法,因此,它不能解决规则30规定的比赛的首要任务。
那么,可以用什么来解决呢? 如果事实证明中心列最终是周期性的,则可以进行计算。 我们知道,最初的十亿步不是周期性的,但是我们至少可以假设可能有数万亿步的过渡过程,之后过渡为周期性。
您认为这是可信的吗?
出现瞬态现象 -从理论上讲(如在
关闭图灵机的经典
问题中 ),它们甚至可以具有任意长度。 在这里,我们看一些示例-在搜索过程中找到-
具有4种可能颜色的规则 (通用代码150898)。 假设我们运行了200步,并且如您所见,中心列将完全是随机的:

代号ArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {200, 150 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]},
PixelConstrained -> 2, Frame -> False]
经过500个步骤,整个模板看起来完全是随机的:

代号ArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {500, 300 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, Frame -> False,
ImagePadding -> 0, PlotRangePadding -> 0, PixelConstrained -> 1]
在这里,您可以看到,在接近中心列时,发生了一些令人惊讶的事情:经过251个步骤之后,中心列似乎重生为一个固定值(或者至少固定为下一百万个步骤):

代号Grid[{ArrayPlot[#, Mesh -> True,
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, ImageSize -> 38,
MeshStyle -> Lighter[GrayLevel[.5, .65], .45]] & /@
Partition[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {1400, {-4, 4}}],
100]}, Spacings -> .35]
规则30会发生同样的转变吗? 考虑规则30中的模式,并选择左侧对角线具有周期性的模式:

代号steps = 500;
diagonalsofrule30 =
Reverse /@
Transpose[
MapIndexed[RotateLeft[#1, (steps + 1) - #2[[1]]] &,
CellularAutomaton[30, {{1}, 0}, steps]]];
diagonaldataofrule30 =
Table[With[{split =
Split[Partition[Drop[diagonalsofrule30[[k]], 1], 8]],
ones = Flatten[
Position[Reverse[Drop[diagonalsofrule30[[k]], 1]],
1]]}, {Length[split[[1]]], split[[1, 1]],
If[Length[split] > 1, split[[2, 1]],
Length[diagonalsofrule30[[k]]] - Floor[k/2]]}], {k, 1,
2 steps + 1}];
transientdiagonalrule30 = %;
transitionpointofrule30 =
If[IntegerQ[#[[3]]], #[[3]],
If[#[[1]] > 1,
8 #[[1]] + Count[Split[#[[2]] - #[[3]]][[1]], 0] + 1, 0] ] & /@
diagonaldataofrule30;
decreasingtransitionpointofrule30 =
Append[Min /@ Partition[transitionpointofrule30, 2, 1], 0];
transitioneddiagonalsofrule30 =
Table[Join[
Take[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]] + 2,
Drop[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]]], {n, 1, 2 steps + 1}];
transientdiagonalrule30 =
MapIndexed[RotateRight[#1, (steps + 1) - #2[[1]]] &,
Transpose[Reverse /@ transitioneddiagonalsofrule30]];
smallertransientdiagonalrule30 =
Take[#, {225, 775}] & /@ Take[transientdiagonalrule30, 275];
Framed[ArrayPlot[smallertransientdiagonalrule30,
ColorRules -> {0 -> White, 1 -> Gray, 2 -> Hue[0.14, 0.55, 1],
3 -> Hue[0.07, 1, 1]}, PixelConstrained -> 1,
Frame -> None,
ImagePadding -> 0, ImageMargins -> 0,
PlotRangePadding -> 0, PlotRangePadding -> Full
], FrameMargins -> 0, FrameStyle -> GrayLevel[.75]]
显然,这里有一个边界将疾病左侧的顺序分隔到右侧。 而且,至少在最初的100,000步左右,边界似乎平均向每一步向左移动了约0.252步-
带有一些随机偏差 :
代号data = CloudGet[
CloudObject[
"https://www.wolframcloud.com/obj/bc470188-f629-4497-965d-\
a10fe057e2fd"]];
ListLinePlot[
MapIndexed[{First[#2], -# - .252 First[#2]} &,
Module[{m = -1, w},
w = If[First[#] > m, m = First[#], m] & /@ data[[1]]; m = 1;
Table[While[w[[m]] < i, m++]; m - i, {i, 100000}]]],
Filling -> Axis, AspectRatio -> 1/4, MaxPlotPoints -> 10000,
Frame -> True, PlotRangePadding -> 0, AxesOrigin -> {Automatic, 0},
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
但是,我们最终如何找出这些波动在什么时候不再显着,以至于它们迫使左侧的命令越过中心列,甚至可能使整个模板具有周期性? 从可用数据来看,这种假设似乎不太可能,尽管我无法确切说明如何确定。
当然,这恰恰是说明存在具有非常长的“瞬态”的系统的情况。 现在考虑素数的分布并计算
LogIntegral [
n ]
-PrimePi [
n ]
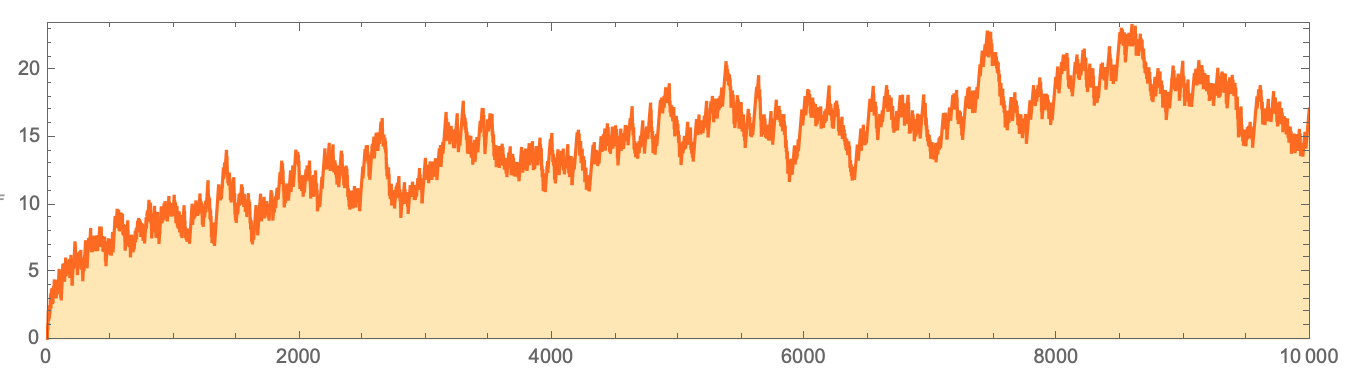
代号DiscretePlot[LogIntegral[n] - PrimePi[n], {n, 10000},
Filling -> Axis,
Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4,
Joined -> True, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
是的,存在波动,但是在此图中,这种差异似乎始终在正区域。 例如,这就是Ramanujan讨论的内容,但最终
结果并非如此 。 最初,他
失败之处的边界在当时是天文数字很大的(
Skives编号 10
10 10 964 )。 而且,虽然还没有人发现显着的值
n的差为负,但已知必须存在高达
n = 10
317 (最终差将为负)。
我认为规则30的中心栏没有发生任何事情,但是到目前为止,我们还没有证据表明这是不可能的,不能争论。
应该注意的是,有可能做出这样的假设:尽管从根本上可以通过显示规则30中心栏中的规律性来证明周期性,但对于非周期性而言,则无法做任何事情。 已知有些模式的中心列是非周期性的,尽管它们非常规则。 此类示例的主要类别是嵌套模板。 例如,这是规则161中的一个非常简单的示例,其中当
n = 2
k时,中心列具有白色单元格:

代号GraphicsRow[
ArrayPlot[CellularAutomaton[161, {{1}, 0}, #]] & /@ {40, 200}]
这是一个
稍微复杂一点的示例(来自两个邻居的2色规则69540422) ,其中中心
列为 Thue-Morse序列 -ThueMorse [
n ]:

代号GraphicsRow[
ArrayPlot[
CellularAutomaton[{69540422, 2, 2}, {{1},
0}, {#, {-#, #}}]] & /@ {40, 400}]
我们可以假定Thue-Morse序列是通过顺序应用替换生成的:

代号RulePlot[SubstitutionSystem[{0 -> {0, 1}, 1 -> {1, 0}}],
Appearance -> "Arrow"]
事实证明,此序列中的
第n个项设置为
Mod [
DigitCount [
n ,2,1],2]-此对象永远不会是周期性的。
规则30的中心栏是否可以通过
替换生成? 如果是这样,那么这个事实会让我感到惊讶(尽管
当出现非常复杂的替代系统时似乎有自然的例子 ),但是只要没有任何证据就可以。
应该注意的是,规则30中的所有竞争性任务都在制定可在无限数量的像元上运行的算法时予以考虑。 ,
n , , ( )? , 2
n —
, , .
n =5:

Graph[# -> CellularAutomaton[30][#] & /@ Tuples[{1, 0}, 4],
VertexLabels -> ((# ->
ArrayPlot[{#}, ImageSize -> 30, Mesh -> True]) & /@
Tuples[{1, 0}, 4])]
=5
n =11:

Row[Table[
Framed[Graph[# -> CellularAutomaton[30][#] & /@
Tuples[{1, 0}, n]]], {n, 4, 11}]]
, , , , . , 2
n ( , ,
).
,
n 30 ,
, 2 n .
, ( ):
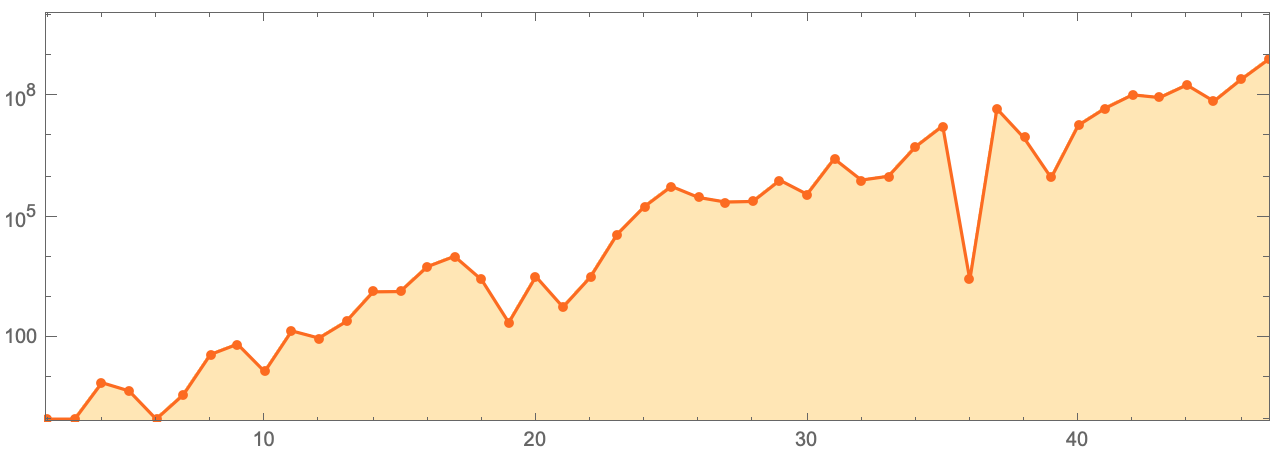
ListLogPlot[
Normal[Values[
ResourceData[
"Repetition Periods for Elementary Cellular Automata"][
Select[#Rule == 30 &]][All, "RepetitionPeriods"]]],
Joined -> True, Filling -> Bottom, Mesh -> All,
MeshStyle -> PointSize[.008], AspectRatio -> 1/3, Frame -> True,
PlotRange -> {{47, 2}, {0, 10^10}}, PlotRangePadding -> .1,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
, ,
n 2
0.63 n . , , . , , ? .
2: ?
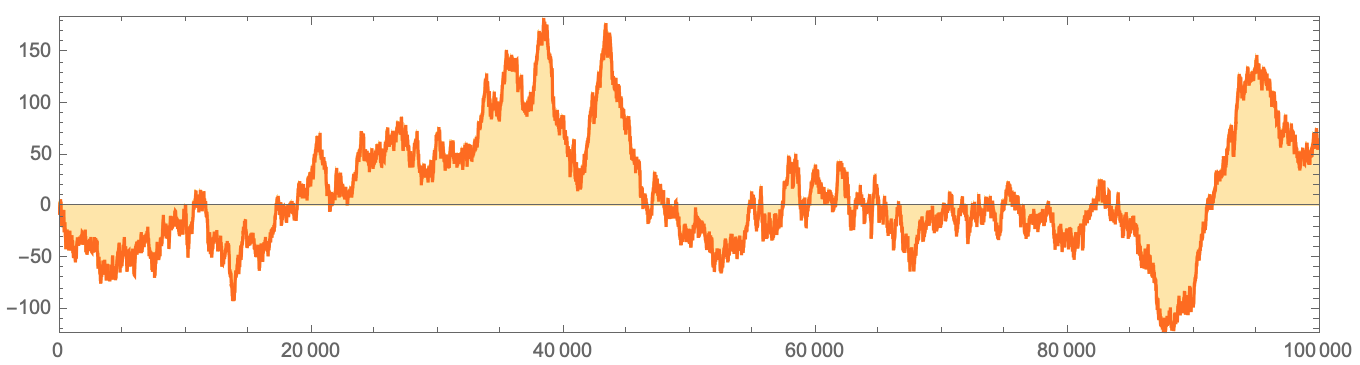
10000 30:
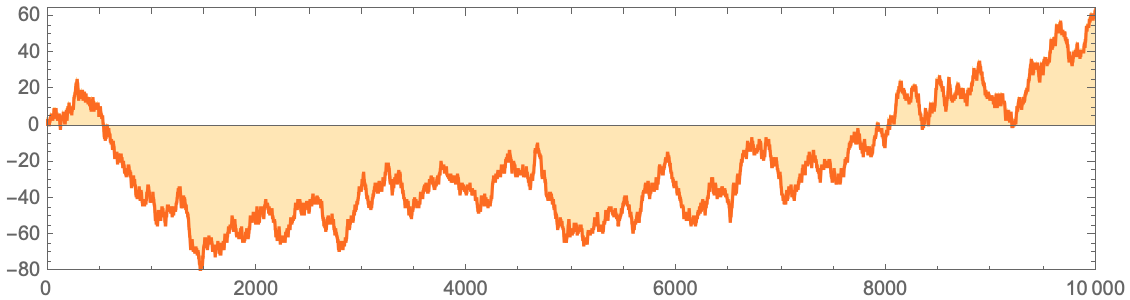
RListLinePlot[
Accumulate[2 CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}] - 1],
AspectRatio -> 1/4, Frame -> True, PlotRangePadding -> 0,
AxesOrigin -> {Automatic, 0}, Filling -> Axis,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
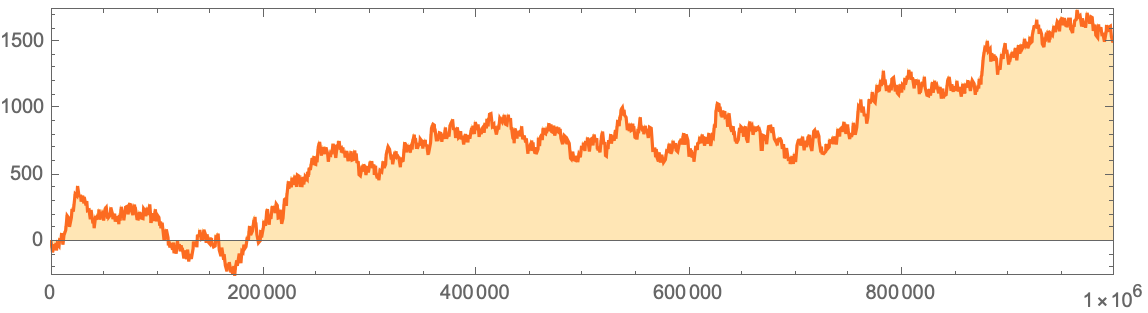
ListLinePlot[
Accumulate[
2 ResourceData[
"A Million Bits of the Center Column of the Rule 30 Cellular Automaton"] - 1], Filling -> Axis, Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4, MaxPlotPoints -> 1000, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
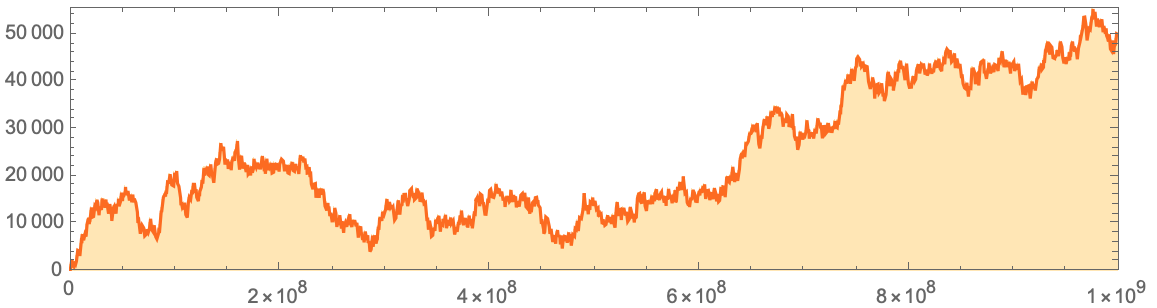
data=Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]];
data=Accumulate[2 data-1];
sdata=Downsample[data,10^5];
ListLinePlot[Transpose[{Range[10000] 10^5,sdata}],Filling->Axis,Frame->True,PlotRangePadding->0,AspectRatio->1/4,MaxPlotPoints->1000,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, , 1 () 0 (), , , , , , , .
. 10 000 :

Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.88, 1.04}}]]
, 1? …
, :
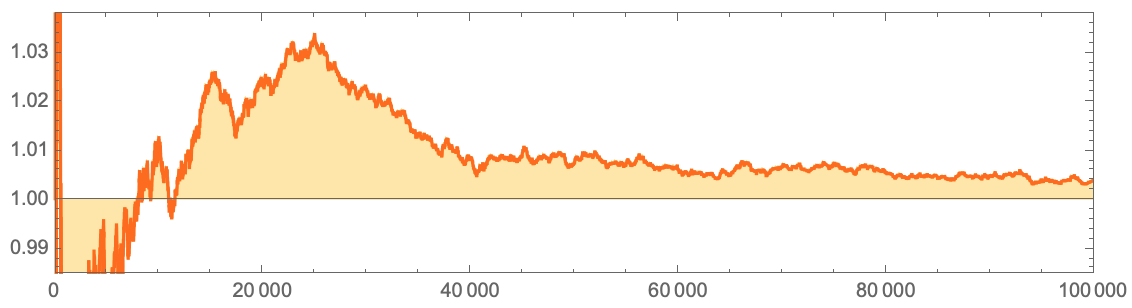
Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^5 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.985, 1.038}}]]
, , . 1 , :
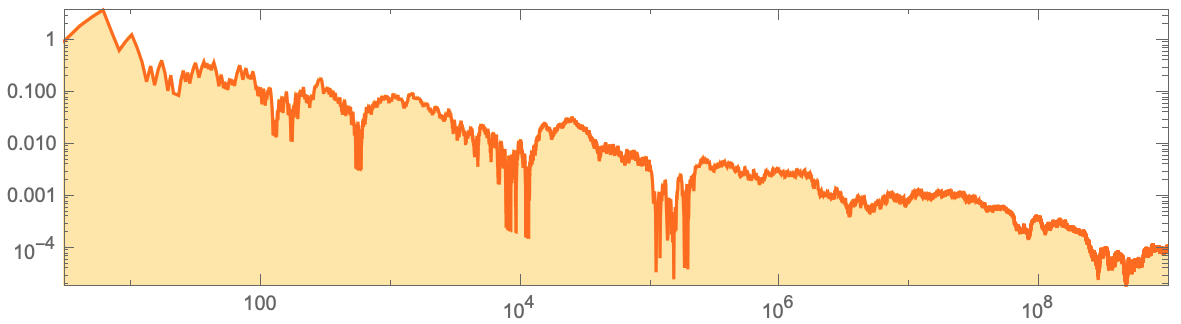
accdata=Accumulate[Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]]];
diffratio=FunctionCompile[Function[Typed[arg,TypeSpecifier["PackedArray"]["MachineInteger",1]],MapIndexed[Abs[N[#]/(First[#2]-N[#])-1.]&,arg]]];
data=diffratio[accdata];
ListLogLogPlot[Join[Transpose[{Range[3,10^5],data[[3;;10^5]]}],Transpose[{Range[10^5+1000,10^9,1000],data[[10^5+1000;;10^9;;1000]]}]],Joined->True,AspectRatio->1/4,Frame->True,Filling->Axis,PlotRangePadding->0,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, ? . , . , , , , .
, , 30, .
, ,
k . , 2
k . , - , , , , 30
k ( ).
,
. , ,
k =22, 2
k , , :

ListLogPlot[{3, 7, 13, 63, 116, 417, 1223, 1584, 2864, 5640, 23653,
42749, 78553, 143591, 377556, 720327, 1569318, 3367130, 7309616,
14383312, 32139368, 58671803}, Joined -> True, AspectRatio -> 1/4,
Frame -> True, Mesh -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.01]}],
PlotTheme -> "Detailed",
PlotStyle -> Directive[{Thickness[.004], Hue[0.1, 1, 0.99]}]]
, , . , –
, , .
—
— , , ,
, , , 30,
, ,
, , .
30 , , «
», , , , , , . , «»: 30, , , , , , , , 30.
, . 30, , - ,
, , 30, , , - .
. 30
, , . , , 30 - ( ), , , , 30. 200 :

ListLinePlot[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {200, {0, 200}}], Mesh -> All,
AspectRatio -> 1/4, Frame -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.0085]}],
PlotTheme -> "Detailed", PlotStyle -> Directive[{
Hue[0.1, 1, 0.99]}], ImageSize -> 575]
, :

Grid[{Table[
Histogram[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {10^n, {0, 20}}], {.01},
Frame -> True,
FrameTicks -> {{None,
None}, {{{0, "0"}, .2, .4, .6, .8, {1, "1"}}, None}},
PlotLabel -> (StringTemplate["`` steps"][10^n]),
ChartStyle -> Directive[Opacity[.5], Hue[0.09, 1, 1]],
ImageSize -> 208,
PlotRangePadding -> {{0, 0}, {0, Scaled[.06]}}], {n, 4, 6}]},
Spacings -> .2]
, , , 0 1.
1900- . , ,
FractionalPart [
hn ]
n h . ,
FractionalPart [
h n ]
h (
), —
FractionalPart [(3/2)
n ] — . (,
, 16- , , 2-
FractionalPart [16
x n -1 +
r [
n ]],
r [
n ]
n .)
3: n- O( n ) ?
,
150 :

Row[{ArrayPlot[CellularAutomaton[150, {{1}, 0}, 30], Mesh -> All,
ImageSize -> 315],
ArrayPlot[CellularAutomaton[150, {{1}, 0}, 200], ImageSize -> 300]}]
, ( ), , :

ArrayPlot[{Table[Mod[IntegerExponent[t, 2], 2], {t, 80}]},
Mesh -> All, ImageSize -> Full]
? , ,
:
Mod [
IntegerExponent [
n , 2], 2]. ,
n , , .
, « »? ,
n ,
Log [2,
n ] . , , O(log
n ) .
- 30? ,
n- , 30
n 2 , , . , -, , , — , , , , , .
« » (,
, . .), , , , , (,
,
3D- . .), .
,
1980- , , , ,
, , , .
, 3 30 , , . ( O(
n ) ; O(
n α ) α <2, , , O(log
β (
n )) — , , .)
3 , ,
n- , O(
n ), 150 .
O (
n )? () , « »?
, — — , , .
,
. , , ,
n , ,
,
n , (, «», O(log
n ) .
, . , , , ,
Wolfram Language . « ». , , Wolfram Language
, .
, 30 , 3 , , , , , ,
n- , O(
n ) , .
, , . , ,
. , , , , , — , O(log
n ) ,
n .
,
P NP . , 30 ( P
LOGTIME ), , , , . , , ,
n n , O(
n 2 ) , , P (« »), , , , , NP. («») , , , , 2
n .
, 2
n , , . ,
NP- , , , NP . 30 NP-? , , ( - , 30
NP).
30 . : 30 , , 30, «» , , , , .
, 256
110 ( , ),
110 , ,
, . , , , «» 110 .

SeedRandom[23542345]; ArrayPlot[
CellularAutomaton[110, RandomInteger[1, 600], 400],
PixelConstrained -> 1]
30, , — , «» , . ,
, 30 , , ,
, .
, , , , , 30. , , (, )
, , . , , — , . , .
, , 3.
,
,
,
,
n- ?
, 30 . , 2
m 2 m ×
m , , . , , , O(
n 2 ) ( ). , O(
n ) ? .
, 1 , , - O(
n ) — , « ». , ( , 2 ), , , .
- , , , ? ,
, .
. «» , , , .
30 - . ( — — 30
Wolfram Language, « !» ).
: «
- , , ». ? , , , - .
. , — , . ,
, , — - «» 30.
,
30. , 30 - . , , , - 30 , , , , — 30, , , , .
. ,
3 2 6 :

Row[Riffle[
ArrayPlot[#, ImageSize -> {Automatic, 275}] & /@ {Table[
IntegerDigits[3^t, 2, 159], {t, 100}],
Table[IntegerDigits[3^t, 6, 62], {t, 100}]}, Spacer[10]]]
, 6
. ( 2 ). , , .
s- n .
s- 3
n , «» (
b — , 2 6)
Mod [
Quotient [3
n , b
s ], b]. ? , 3
n n , : , , 3
n , log(
n ). , ,
, . , 30, , - , .
3
n -
30 , , O(
n ), ,
n , . ,
r [
n ] ,
r [
n ] «O-»
n , ,
MaxLimit [
r [
n ]/
n ,
n →∞ ]<∞.
, ( - ), . ,
r [
n ]
n , , , - , ,
r [
n ]
. , -
n ( - ),
r [
n ] . , , ,
r [
n ] O(
n ).
30
, ( , ).
Wolfram Language
t 30 :
![c [t_] c [t_]](https://habrastorage.org/getpro/habr/post_images/219/e07/f8e/219e07f8ec41111ce3457989e3d3c188.png)
c[t_] := CellularAutomaton[30, {{1}, 0}, {t, {{0}}}]
[
t ].
1: ?

\!\(
\*SubscriptBox[\(\[NotExists]\), \({p, i}\)]\(
\*SubscriptBox[\(\[ForAll]\), \(t, t > i\)]c[t + p] == c[t]\)\)

NotExists[{p, i}, ForAll[t, t > i, c[t + p] == c[t]]]
,
t >
i ,
[
t +
p ]
c [
t ].
2: ?

\!\(\*UnderscriptBox[\(\[Limit]\), \(t\*
UnderscriptBox["\[Rule]",
TemplateBox[{},
"Integers"]]\[Infinity]\)]\) Total[c[t]]/t == 1/2

DiscreteLimit[Total[c[t]]/t, t -> Infinity] == 1/2
[
t ]/
t t →∞ 1/2.
3: n- O( n ) ?
machine[
m ] ,
m (,
TuringMachine [...]), machine[
m ][
n ] {
v ,
t },
v — ,
t — (, ). :
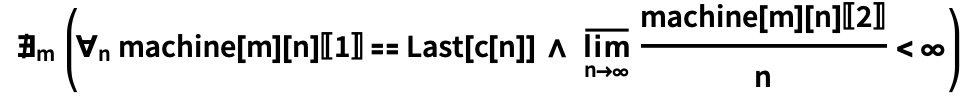
\!\(
\*SubscriptBox[\(\[NotExists]\), \(m\)]\((
\*SubscriptBox[\(\[ForAll]\), \(n\)]\(\(machine[m]\)[n]\)[[1]] ==
Last[c[n]]\ \[And] \
\*UnderscriptBox[\(\[MaxLimit]\), \(n -> \[Infinity]\)]
\*FractionBox[\(\(\(machine[m]\)[n]\)[[
2]]\), \(n\)] < \[Infinity])\)\)
« m, , machine[
m ]
n c [
n ] ,
n , ». (
m , «» ).
, , , , . 3 ( ), , 1 2, . 3 ( ), , 1 . :
1 , , 3 .
1 , , , , , 2. , 2 - 3. ,
, O(
n ) — , , 3, , .
, , ?
1 , , , 30 - , . , 1 , . , , - , .
( , ), 2, 3 , — , , , . , 3 , , (, , ), O(
n ) .
, - . ,
n n- . . , - , . , ,
n n . , . , « » . ,
n , . , , O(
n ) .
:
? « »,
/
( ).
, , (
)? , , , , «» , -, ( ) , .
, ,
. , , , . , () .
, , , , : «
». , , , .
, — - . -
n , . . — («
» . .). , , , .
— , , . , (
FindEquationalProof ). , ()
.
,
, , — , . — , .
, .
Wolfram|Alpha (, ) , . , .
, , -
, , , , .
? ,
«» , .
Wolfram Language , . Wolfram Language, .
« »? , , - . . - , , «» , , - ( ), . , , «» — , .
?
, ? . . , . - , . . - , , .
, , «» — , — , « ». ,
2,3 2007 .
— , , 30, , .
. - ( , , ). , , ( ) , , .
n — 30
n ,
n .
Wolfram Language . , 0,4 100 000 :

CellularAutomaton[30, {{1}, 0}, {100000, {{0}}}]; // Timing
,
30 Xor [
p ,
Or [
q ,
r ]],
.
,
CellularAutomaton :

Module[{a = 1},
Table[BitGet[a, a = BitXor[a, BitOr[2 a, 4 a]]; i - 1], {i,
100000}]]; // Timing
.
. , , 30, , 30 , , , : .
. , , «»
. 30 — . , , , .
— , , . , , 30, .
, , 30,
. 45° , 30, , . ; . ?
? ? - ?
, , , , , .
?
30, . , , ,
, ,
. , - , , ,
, , , - .
– , «» .
( , - ). , , , ,
« » :

GraphicsRow[(ArrayPlot[
CellularAutomaton[30,
MapAt[1 - #1 &, Flatten[Table[#1, Round[150/Length[#1]]]], 50],
100]] &) /@ {{1, 0}, {1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0}, {1,
0, 0, 0, 0, 0, 0}, {1, 1, 1, 0, 0}}]
, , , . ? , « » ?
, (, ), , - 30?
« 30». , «» ? 30 , ? «» ?
, , 30, , , , 30, . 256 ( ) , , :

Row[Riffle[
Labeled[ArrayPlot[CellularAutomaton[#, {{1}, 0}, {150, All}],
PixelConstrained -> 1, Frame -> False],
Style[Text[StringTemplate["rule ``"][#]], 12],
LabelStyle -> Opacity[.5]] & /@ {45, 73}, Spacer[8]]]
, . , . ,
, . , , , « 30», .
« 30». 30 ( 1), , — , .
2, 30, , .
3 .
n- O(
n γ ) γ <2 ( - )? ,
n- , O(log(
n )) ? O(log(
n )) ? ? . ?
, 30. 30, (, , 110) , 30.
, NP-, 30 , , NP-? , . , , , « », 30?
?
2007 2,3 , — , , , . , . 30? 我不知道 40 , - ( , !). , , (, ) .
, - ( ), , , , , , , . ( ), , , .
, « » ( , ), . , . , (« » . .). . , - « », , , …
, . , , . , , . , .
, 30 40 , - .
Wolfram Language?
« Wolfram » ( ).