
在本文中,从最小的细节开始,详细考虑了三种获取Euler-Poisson积分的方法。 在一种方法中,推导了辅助还原公式。 要找到一些复杂的积分,可以使用简化公式,该公式可以减小被积数的阶数并以有限的步数计算相应的积分。
该积分取自高斯函数:
I= int limit 0inftye−x2dx有一种非常有趣的数学方法。 要找到原始积分,请先寻找该积分的平方,然后从结果中取根。 怎么了 是的,因为去极坐标非常容易,而且很轻松。 因此,请考虑高斯积分的平方:
I ^ 2 = \ int \ limit_0 ^ \ infty {e ^ {-x ^ 2} dx} \ int \ limit_0 ^ \ infty {e ^ {-y ^ 2} dy} = \ int \ limit_0 ^ \ infty { \ int \ limits_0 ^ \ infty {e ^ {-\ left({x ^ 2 + y ^ 2} \ right)}}}} dxdyI ^ 2 = \ int \ limit_0 ^ \ infty {e ^ {-x ^ 2} dx} \ int \ limit_0 ^ \ infty {e ^ {-y ^ 2} dy} = \ int \ limit_0 ^ \ infty { \ int \ limits_0 ^ \ infty {e ^ {-\ left({x ^ 2 + y ^ 2} \ right)}}}} dxdy我们看到我们得到了一些函数的双重积分
g\左(x,y\右)= exp\左[−左(x2+y2\右)\右] 。 该表面积分的最后是笛卡尔坐标系中的面积元素
dS=dxdy 。
现在让我们转到极坐标系:
beginarrayldS=dxdy=rd varphi cdotdr\向左。 \开始arraylx=r cos varphiy=r sin varphi endarray right| tox2 cos2 varphi+y2 sin2 varphi=r2 tox2+y2=r2 endarray
此处应注意,r可以从0到+∞变化,因为 x在相同范围内变化。 但是角度φ在0到π/ 2之间变化,描述了笛卡尔坐标系第一季度的积分区域。 替换源,我们得到:
\ begin {array} {l} I ^ 2 = \ int \ limits_0 ^ \ infty {\ int \ limits_0 ^ \ infty {e ^ {-\ left({x ^ 2 + y ^ 2} \ right)}}} } dxdy = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ int \ limits_0 ^ \ infty {e ^ {-r ^ 2}}} rd \ varphi dr = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {-r ^ 2} rdr} = \ int \ limits_0 ^ {\ frac {\ pi} {2}} { d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {-r ^ 2} \ frac {1} {2} d \ left({r ^ 2} \ right)} = \\ = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left({\ left。{-e ^ {-r ^ 2}} \ right | _0 ^ \ infty} \ right)= \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left({-e ^ {-\ infty}-\ left({ -e ^ 0} \ right)} \ right)= \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} {2 } \左({\左。\ varphi \右| _0 ^ {\ frac {\ pi} {2}}} \右)= \ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \到I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}
由于积分的对称性和被积分值的正范围,我们可以得出以下结论:
int limits − inftyinftye−x2dx=2 int limits 0inftye−x2dx=2 cdot frac sqrt pi2= sqrt pi
让我们找到更多解决方案? 这很有趣! :)
考虑功能
g\左(t\右)=\左(1+t\右)e−t现在让我们回想起学校的数学,并使用导数和极限对函数进行简单的研究。 并不是说我们会在这里考虑复杂的极限(毕竟,它们在学校没有通过),我们只是讨论如果函数的自变量趋于零或无穷大时函数会发生什么,因此我们将估计渐近行为,这在数学中总是非常重要的。 这就像对所发生情况的定性评估。
\开始数组lg\左(t\右)=\左(1+t\右)e−tg′\左(t\右)=e−t−\左(1+t\右)e−t=−te−tg′\左(t\右)=0\到t=0\左[\开始数组lt<0\到−te−t>0\到g\左(t\右)− rm增加t>0\到−te−t<0\到g\左(t\右)− rm减少\结束array\右。g\左(0\右)=\左(1+0\右)e−0=1g\左(−1\右)=\左(1−1 right)e−\左(−1 right)=0g\左( infty right)=\左(1+ infty right)e− infty=0 endarray
它的上限在区间(-∞; +∞)上为零,在区间[-1; +∞)上为零。
我们对变量进行以下更改
t= pmx2我们得到:
t = \ pm x ^ 2 \到\左\ {\开始{array} {l} 0 <\左({1-x ^ 2} \ right)e ^ {x ^ 2} <1 \\ 0 < \左({1 + x ^ 2} \右)e ^ {-x ^ 2} <1 \\ \结束{array} \右。 \至\左\ {\开始{array} {l} 0 <\左({1-x ^ 2} \ right)<e ^ {-x ^ 2} \\ 0 <e ^ {-x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ right。
在第一个不等式中,我们限制变化(0,1),在第二个不等式中,我们限制间隔(0; +∞),将两个不等式都提高到n的幂,因为带正项的不等式可以提高到任何正数。 我们得到:
\ begin {array} {* {20} c} {\左\ {\ begin {array} {l} \左({1-x ^ 2} \ right)^ n <e ^ {-nx ^ 2} \\ 0 <x <1 \\ \结束{array} \ right。}&{\左\ {\开始{array} {l} e ^ {-nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ right)^ n}} \\ x> 1 \\ \ end {array} \ right。} \\ \ end {array}
让我们构造n = 1的图以证明不等式
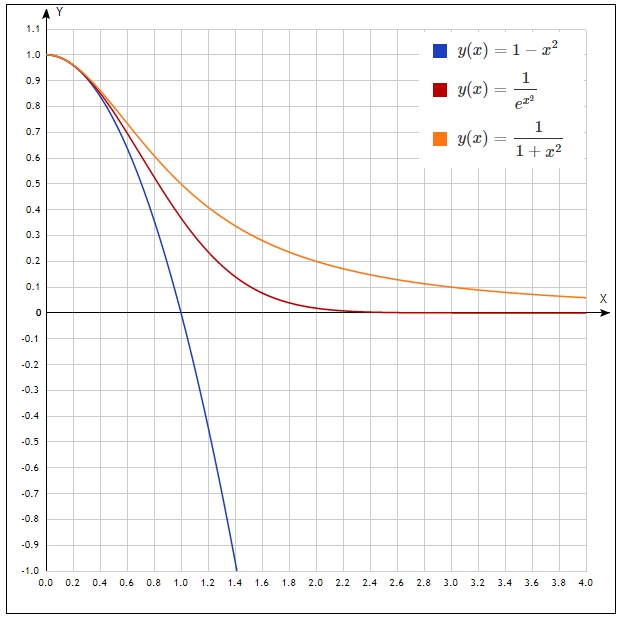
现在,我们尝试将不等式整合到相应系统中指示的范围内。 并立即将所有内容合并为一个不等式:
int limits10\左(1−x2 right)ndx< int limits10e−nx2dx< int limit 0inftye−nx2dx< int limit 0infty frac1\左(1+x2 right)ndx
同样,如果您查看图表,则该不等式是正确的。
给定一个小的替换,很容易看到:
int limits 0inftye−nx2dx= left[ beginarraylp= sqrtnxp2=nx2 fracdp sqrtn=dx endarray right]= frac1 sqrtn int limits 0inftye−p2dp= frac1 sqrtn我
即 在中间的那个大不等式中,我们有Euler-Poisson积分,现在我们需要找到站在该不等式边界的积分。
从左边界找到积分: beginarrayl int limits10\左(1−x2 right)ndx=\左[ beginarray∗20c beginarraylx= sintdx= costdt1−x2=1− sin2t= cos2t endarray&\开始arraylx=1\到t= arcsin1= frac pi2x=0\到t= arcsin0=0 endarray endarray right]== int limits frac pi20 cos2nt cdot costdt= int Limit frac pi20 cos2n+1tdt endarray
为了计算和评估它,我们首先找到一个一般积分。 现在,我将向您展示如何针对给定的积分导出简化公式(在数学中,通过这种公式,它们意味着降低度)。
beginarrayl int limits alpha beta cosntdt= int limits alpha beta cosn−1t costdt= int limits alpha beta cosn−1t cdotd left( sint right)== left[\开始array∗20cu= cosn−1t&du=−\左(n−1 right) cosn−2t sintdtdv=d\左( sint right)&v= sint endarray right]==\左。 cosn−1t sint\右| alpha beta+\左(n−1\右) int limits alpha beta cosn−2t sin2tdt==\左。 cosn−1t sint\右| alpha beta+\左(n−1\右) int limits alpha beta cosn−2t\左(1− cos2t\右)dt==\左。 cosn−1t sint\右| alpha beta+\左(n−1\右) int limits alpha beta cosn−2tdt−\左(n−1\右) int limits alpha beta cosntdt endarray
\开始arrayl int limits alpha beta cosntdt=\左。 cosn−1t sint\右| alpha beta+\左(n−1\右) int limits alpha beta cosn−2tdt−\左(n−1\右) int limits alpha beta cosntdt int limits alpha beta cosntdt+\左(n−1\右) int limits alpha beta cosntdt=\左。 cosn−1t sint\右| alpha beta+\左(n−1\右) int limits alpha beta cosn−2tdtn int limits alpha beta cosntdt=\左。 cosn−1t sint\右| alpha beta+\左(n−1\右) int limits alpha beta cosn−2tdt int limits alpha beta cosntdt= frac1n\左。 cosn−1t sint\右| alpha beta+ fracn−1n int limits alpha beta cosn−2tdt endarray
现在,如果使用归约公式,我们考虑相同的积分,但极限范围为0到π/ 2,则可以进行一些简化:
\开始arrayl int limits frac pi20 cosntdt= frac1n\左。 cosn−1t sint right| frac pi20+ fracn−1n int limits frac pi20 cosn−2tdt=\左[ frac1n\左。 cosn−1t sint right| frac pi20=0 right]== fracn−1n int limits frac pi20 cosn−2tdt= fracn−1n left( frac1n−2\左 cosn−3t sint\右| frac pi20+ fracn−3n−2 int limits frac pi20 cosn−4tdt right)== fracn−1n\左( fracn−3n−2 int limits frac pi20 cosn−4tdt right)= fracn−1n left( fracn−3n−2 left( fracn−5n−4 int limits frac pi20 cosn−6tdt right) right)== fracn−1n\左( fracn−3n−2\左( fracn−5n−4\左( fracn−7n−6 int limits frac pi20 cosn−8tdt right) right) right)=... endarray
如我们所见,您可以将其降低到无穷大(取决于n)。 但是,有一个微妙之处。 公式根据n是否为偶数而变化。
为此,我们考虑两种情况。
\ begin {array} {l} n = 10:\\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\左({{frac {1 } {2} + \ frac {1} {2} \ cos 2t} \ right)dt} = \\ = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \左。 {\左({\ frac {1} {2} t + \ frac {1} {2} \ sin 2t} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ cdot \ frac {\ pi} {4} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 4 \ cdot 2}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{\左({n -1} \对)!!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}
beginarrayln=9: int limits frac pi20 cos9tdt= frac8 cdot6 cdot4 cdot29 cdot7 cdot5 cdot3 int limits frac pi20 costdt= frac8 cdot6 cdot4 cdot29 cdot7 cdot5 cdot3左。\左( sint right)\右| frac pi20== frac8 cdot6 cdot4 cdot29 cdot7 cdot5 cdot3 cdot1= frac\左(n−1\右)!!n!!\结束array
n在哪里! -双阶乘。 n的双阶乘由n表示! 并定义为间隔[1,n]中所有自然数的乘积,奇偶性与n
由于对于任何n值,2n +1是一个奇数,因此我们得到了不等式的左边界:
\ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\左({2n} \右)!!}}} {{\左({2n + 1} \对)!!}}
从右边界找到积分:(这里我们使用先前证明的相同的折减公式)
beginarrayl int limits 0infty frac1 left(1+x2 right)ndx= left[ beginarraylx= tant\至\开始array∗20cx=0\至t=0x= infty\至t= frac pi2 endarraydx= fracdt cos2t frac11+x2= frac11+ tan2t= cos2t endarray right]== int limit frac pi20 cos2n−2tdt=\左[\左(2n−2\右)− rmeven右]= frac\左(2n−3\右)!!\左(2n−2\右)!! cdot frac pi2 endarray
在估计了不等式的左侧和右侧之后,我们进行了一些转换以评估不等式的左侧和右侧的极限,条件是n趋于∞:
\开始{array} {l} \ frac {{\左({2n} \右)!!}}} {{\左({2n + 1} \右)!!}} <\ frac {1} { {\ sqrt n}} \ cdot I <\ frac {{\左({2n-3} \右)!!}}} {{\左({2n-2} \右)!!}}} \ cdot \ frac {\ pi} {2} \\ \ sqrt n \ cdot \ frac {{\左({2n} \右)!!}}} {{\左({2n + 1} \右)!!}} <I <\ sqrt n \ cdot \ frac {{\左({2n-3} \右)!!}}} {{\左({2n-2} \右)!!}}} \ cdot \ frac {\ pi} {2} \\ \结束{array}
平方不等式两边:
n cdot frac\左(\左(2n\右)!!\右)2\左(\左(2n+1\右)!! right)2<I2<n cdot frac\左(\左(2n−3\右)!!\右)2\左(\左(2n−2\右)!!\右)2 cdot frac pi24
现在让我们做一点题外话。 1655年,约翰·沃利斯(John Wallis)(英国数学家,数学分析的先驱之一。)提出了确定数π的公式。 J. Wallis来到她身边,计算了一个圆的面积。 该乘积收敛极慢;因此,Wallis公式对数π的实际计算几乎没有用。 但这对评估我们的表情非常有用:)
pi= mathop lim limitesn to infty frac1n left[ frac left(2n right)!!\左(2n−1\右)!!\右]2
现在,我们变换不等式,以便可以看到在哪里可以替代Wallis公式:
beginarrayl fracn2\左(2n+1 right)2 cdot frac1n cdot frac\左(\左(2n\右)!!\右)2\左(\左(2n−1\右)!!\右)2<I2< frac1 frac1n cdot frac left( left(2n−2 right)!! right)2\左(\左(2n−3\右)!!\右)2 cdot frac pi24 mathop lim limitsn to infty\左[ fracn2\左(2n+1\右)2\右] cdot mathop lim limitsn\到 infty\左[ frac1n cdot frac\左(\左(2n\右)!!\右)2\左(\左(2n−1\右)!!\右)2\右]<I2< frac1 mathop lim limitsn to infty\左[ frac1n cdot frac\左(\左(2n−2\右)!!\右)2\左(\左(2n−3\右)!!\右)2\右] cdot frac pi24 frac14 cdot pi<I2< frac1 pi cdot frac pi24\到 frac pi4<I2< frac pi4I2= frac pi4 toI= frac sqrt pi2 endarray
从Wallis公式得出,当n→∞时,左右表达式都趋于π/ 4
由于函数exp [-x²]是偶数的事实,我们可以安全地假定
int limits − inftyinftye−x2dx=2 int limits 0inftye−x2dx=2 cdot frac sqrt pi2= sqrt pi
欧拉在1729年首次计算了一维高斯积分,然后泊松找到了一种简单的计算方法。 在这方面,它被称为欧拉-泊松积分。
让我们尝试计算高斯积分。 它可以用不同的形式编写。 毕竟,什么都没有改变进行集成的变量的名称。
beginarraylI= int limits 0inftye−x2dxI= int limits − inftyinftye−x2dx= int limits − inftyinftye−y2dy= int limits − inftyinftye−z2dz\结束array
您可以从三维笛卡尔坐标系转到球面坐标系,并考虑高斯积分的立方。
\ left \ {\ begin {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {array} \对。 \到x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2
该变换的雅可比公式可计算如下:
\开始arraylJ= left| beginarray∗20c frac\部分x\部分r& frac\部分x\部分 theta& frac\部分x\部分 varphi frac\部分y\部分r& frac\部分y\部分 theta和 frac\部分y\部分 varphi frac\部分z\部分r& frac\部分z\部分 theta& frac\部分z\部分 varphi\结束array\对|=\左| beginarray∗20c sin theta cos varphi&r cos theta cos varphi&−r sin theta sin varphi sin theta sin varphi和r cos theta sin varphi&r sin theta cos varphir cos theta&−r sin theta&0 endarray right|==r2 sin theta endarray
\ begin {array} {l} I ^ 3 = \ int \ limits_ {-\ infty} ^ \ infty {\ int \ limits_ {-\ infty} ^ \ infty {\ int \ limits {{\ infty} ^ \ infty {e ^ {-x ^ 2-y ^ 2-z ^ 2}} dxdydz}} = \ int \ limits_0 ^ {2 \ pi} {\ int \ limits_0 ^ \ pi {\ int \ limits_0 ^ \ infty { e ^ {-r ^ 2} Jdrd \ theta d} \ varphi =}} \\ = \ int \ limit_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ \ pi {\ sin \ theta d \ theta} \ int \ limit_0 ^ \ infty {e ^ {-r ^ 2} r ^ 2 dr} \\ \ end {array}
我们从内部开始依次计算积分。
beginarrayl int limits 0inftye−r2r2dr= left[ beginarraylu=r todu=drdv=re−r2dr\到v= intre−r2dr= frac12 inte−r2dr2=− frac12e−r2 endarray right]== left。\左(− frac12re−r2 right)\右| 0infty+ frac12 int limits 0inftye−r2dr= frac12 int limits 0inftye−r2dr= frac12 cdot fracI2= fracI4 int limit 0pi sin thetad theta=\左。\左(− cos theta\右)\右| 0pi=\左(− cos pi\右)−\左(− cos0\右)=1+1=2 int limits2 pi0d varphi=\左。 varphi right|2 pi0=2 pi endarray
然后结果是:
beginarraylI3=2 pi cdot2 cdot fracI4\至I3= piI\至I2= pi\至I= sqrt piI= int limits − inftyinftye−x2dx= sqrt pi endarray
欧拉-泊松积分通常用于概率论中。
我希望这篇文章对某人有用,并有助于理解一些数学技巧:)