初次接触拟牛顿法的人可能会惊讶两次。 首先,快速浏览一下公式后,人们怀疑这是否完全可行。 但是,它们可以工作。 此外,它们能否运作良好似乎值得怀疑。 而且,与梯度下降的各种变化相比,它们的速度要快得多,这不仅令人惊奇,而且不是在特殊构造的任务上,而是在实践中得到的真实任务上。 而且,如果在此之后仍然充满疑虑,那么您需要了解为什么这一切都奏效。
已经考虑了驱动梯度方法(包括牛顿法)的起源和基本思想。 即,我们依靠有关函数在当前位置附近的行为的信息,这为我们提供了简单的数学分析。 至少假设我们可以获取有关一阶导数的信息。 如果这是我们可以使用的全部呢? 梯度下降是我们的句子吗? 当然,是的,除非您突然想起我们正在处理正确处理目标函数的过程。 如果是这样,为什么我们不使用有关函数行为的累积信息来使我们在函数表面上的走动少一点点呢?
使用有关所覆盖路径的信息的想法是大多数加快下降方法的方法的核心。 本文讨论了一种最有效但不是最便宜的会计方法来处理此类信息,从而提出了拟牛顿法的思想。
为了了解拟牛顿方法的支线从何而来以及名称从何而来,我们再次必须返回基于固定点方程直接解的极小化方法
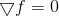
。 正如考虑将牛顿法应用于该方程的解使我们找到同名的优化方法(与它的祖先不同,它具有一个全局收敛的区域),我们可以期望考虑其他方法来求解非线性方程组将在规划构建其他优化方法的想法。
正割方法
让我提醒您,牛顿法用于解方程组

,是基于接近解的某个点附近的替换

功能

它的线性近似

在哪里
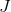
是线性运算符,

是向量,

对每个变量具有偏导数,与雅可比矩阵重合
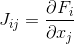
。 接下来,方程式求解
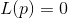
并指出
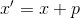
作为所需解决方案的新近似值。 它很简单,而且有效。
但是,如果由于某种原因我们无法计算雅可比矩阵怎么办? 在这种情况下,首先想到的是,如果我们不能通过分析来计算偏导数,那么我们就可以很好地得到它们的数值近似值。 这种近似的最简单(尽管决不是唯一的)选择可以是右有限差分的公式:
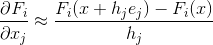
在哪里
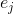
是第j个基向量。 由这些近似组成的矩阵将用

。 更换多少的分析
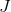
在

在牛顿的方法中,它的收敛性会影响大量的工作,但是在这种情况下,我们会对另一个方面感兴趣。 即,这种近似需要在N个附加点处计算该函数,此外,该函数

在这些点上
插值函数

,即
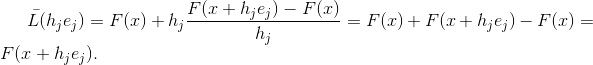
并非Jacobi矩阵的每个近似都具有此属性,但是具有此属性的仿射函数的每个矩阵都是Jacobi矩阵的近似。 确实,如果

和
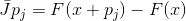
然后在

。 该属性,即插值属性,为我们提供了一种构造方法来推广牛顿法。
让
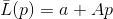
-功能满足要求

对于某些线性独立矢量系统

。 这样的函数称为
割线函数

,定义它的方程是
割线方程 。 如果向量系统

是完整的(也就是说,它们中正好有N个,并且它们仍然是线性独立的),此外,向量系统
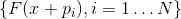
然后线性独立
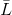
唯一定义。
任何基于方程局部变化的方法

形式方程

在哪里
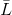
满足
割线方程 ,称为
割线方法 。
关于如何以最合理的方式构造函数割线的问题出现了。

。 下面的推理似乎很明显:让一个仿射模型在点x处构建,并在这些点上插入给定函数

。 方程解

给我们一个新点
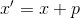
。 然后在某个点建立仿射模型
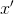
选择插值点以使该值最合理

已经知道-也就是说,从集合中取出它们
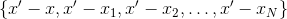
。 有多种选择,可以从以前使用的许多点中进行选择。 例如,您可以将那些
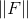
无关紧要或仅是第一

点。 无论如何,似乎很明显

新仿射模型的许多插值点中应包含该元素。 所以超越
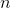
我们集合中的迭代过程的步骤最多
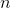
基于先前通过的点的位移。 如果流程的构建方式使得新的仿射模型不再使用

取先前值的一个,则此过程称为p点割线方法。
乍一看,似乎N点割线法是替代牛顿法的最佳人选,因为它最大程度地利用了我们在求解过程中获得的信息,同时最大程度地减少了其他计算的次数-我们在后者中使用函数的值N分通过。 不幸的是,事实并非如此。 问题是向量系统
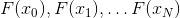
固执地拒绝以足够大的N来进行线性独立。此外,即使事实证明该条件得到满足并且相应的仿射模型仍然存在,方向还是有可能

也证明是线性独立的,结果甚至更少。 这就导致了一个事实,即仿射模型虽然存在,但仍然退化并且实际上不适合。
通常,最稳定的是2点割线方法。 也就是一种方法,在该方法中,每次迭代我们都必须计算该函数的其他N-1个值。 这显然不适合我们的实际目的。
然后的问题是-这都是什么?
拟牛顿法求解方程
出路很简单,尽管并不明显。 如果我们没有基于已经计算出的值的技术能力来唯一确定满足割线方程的仿射模型,则没有必要。 我们以割线方程为基础,但是我们将要求仅对某些不完整的向量系统满足

。 换句话说,我们将要求仅对于足够少量的已知值满足内插条件。 当然,在这种情况下,我们不能再保证在这种模型中使用的矩阵趋向于Jacobi矩阵,但是我们将不需要它。 除此之外,仿射模型必须在当前点内插函数,即

,我们得到以下割线方法的公式:
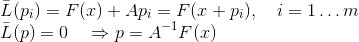
Bruiden是第一个在m = 1时考虑这种方法的人,称它们为准牛顿法。 显然,这种情况下的割线条件使我们能够唯一地识别矩阵

仅当对其施加了附加条件时,并且每个此类附加条件都会产生单独的方法。 布吕登本人的理由如下:
作为方向的运动  从点
从点  到这一点
到这一点  除了以下功能外,我们没有提供其他任何有关功能变化的信息:
除了以下功能外,我们没有提供其他任何有关功能变化的信息:  方向,然后新的仿射函数对向量的影响
方向,然后新的仿射函数对向量的影响  应该与旧函数对相同向量的影响不同,相差越小,差异越大
应该与旧函数对相同向量的影响不同,相差越小,差异越大  来自
来自  。 不得已时
。 不得已时  正交的
正交的  ,新功能的行为不应与旧功能的行为有所不同。
,新功能的行为不应与旧功能的行为有所不同。
Breiden的想法非常简单。 的确,如果我们没有有关函数行为的新信息,那么我们能做的最好的事情就是尽量不要破坏旧函数。 然后附加条件

对于所有

这样

允许您唯一地确定新转换的矩阵-通过向旧矩阵添加等级1校正获得。
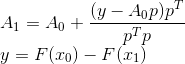
但是,尽管Bruiden得出的结论简单而一致,但它们并未提供可作为构建其他类似方法基础的支点。 幸运的是,他的想法有了更正式的表达。 即,以此方式构造的矩阵

原来是解决以下问题的方法:
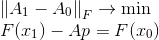
任务约束不过是割线方程,最小化条件反映了我们希望在矩阵中保存尽可能多的信息的愿望。
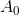
。 在这种情况下,矩阵之间的差异的度量是Frobenius范数,其中提出的问题具有明确的解决方案。 该配方很可能作为构建其他方法的起点。 即,我们既可以改变评估引入的变化的
度量 ,也可以改变施加在矩阵上的
条件 。 通常,人们已经可以使用这种方法的表述。
拟牛顿优化方法
了解了主要思想之后,我们终于可以回到优化问题,并注意到应用Bruyden公式重新计算仿射模型并不完全适合我们的任务。 实际上,梯度函数的一阶导数
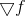
除了Hessian矩阵外,没有其他任何东西,该矩阵通过构造是对称的。 同时,根据Bruyden规则进行更新会导致矩阵不对称

即使
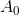
是对称的。 这并不意味着不能使用Bruden方法求解固定点方程,而是基于这样的更新规则,我们不太可能构造好的优化方法。 通常,很明显,拟牛顿法的效果更好,问题的条件系统描述特定Jacobi矩阵的特征越准确。
为了纠正这一缺陷,我们向Bruden最小化问题添加了一个附加约束,明确要求新矩阵与旧矩阵对称:
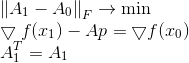
解决这个问题的方法是

在这里
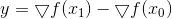
,矩阵重新计算公式以其创建者Powell,Shanno和Bruyden(PSB)命名。 所得矩阵是对称的,但显然不是正定的,如果只是突然的话

不会共线

。 而且,我们
看到在优化方法中非常需要积极的确定性。
再次,我们将校正问题的条件,这次使用缩放的Frobenius范数作为矩阵散度的度量。
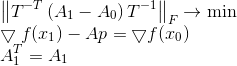
这样的问题陈述的起源是一个单独的大话题,但是有趣的是,如果矩阵T如此
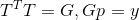
(也就是说,G还是一个满足方向p割线方程的仿射变换矩阵),那么该问题的解决方案就与T的选择无关,并得出更新公式

被称为Davidon-Fletcher-Powell公式。 此更新方法已在实践中证明自己,因为它具有以下属性:
如果  和
和 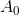 正定则
正定则  也得到肯定的肯定。
也得到肯定的肯定。之后我注意到,如果不满足第一个条件,则不存在具有满足割线方程的正定矩阵的仿射函数。
如果在导致DFP方法的问题中,我们采用仿射模型之间的距离作为衡量仿射模型差异的指标,而不是矩阵本身之间的距离,则得出以下形式的问题:

它的解决方案是一个众所周知的公式,几乎由Breiden,Fletcher,Goldfarb和Shanno(BFGS)同时发现。

迄今为止,据信从计算的角度来看,根据该公式的重新计算是最有效的,并且同时不易发生具有大量迭代的矩阵退化。 在与DFP相同的条件下,此公式保留正定性。
所有描述的更新矩阵的方法都需要校正2级。这使得矩阵求逆变得容易。

使用Sherman-Morrison公式和值

。
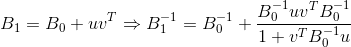
前提是公式的分母为非零。 我不会给出用于更新所列方法的逆矩阵的特定公式,因为它们很容易独立地找到或推导。 在这种情况下,唯一需要注意的是,与更新原始矩阵相比,用于更新逆矩阵的方法的变体通常不稳定得多(也就是说,它们遭受舍入误差的影响更大)。 最有效的方式不是更新矩阵本身,而是更新其Cholesky分解(当然除非进行这样的分解),因为这样的实现选项在数值上更稳定,此外还使求解确定运动方向的方程的成本最小化。
仍然需要考虑在准牛顿过程中第一个矩阵应如何显示的问题。 这里的一切都是显而易见的-它越接近于Hessian矩阵或它的校正版本,如果Hessian突然没有变成正定,从收敛的角度来看,它将越好。 但是,原则上,任何正定矩阵都适合我们。 这种矩阵的最简单形式是单个矩阵,然后第一次迭代与梯度下降的迭代重合。 Fletcher和Powell表明(对于DFP方法而言,自然),如果将二次函数最小化,则无论使用哪个(正定)矩阵作为初始DFP迭代,它们都会导致N次迭代的解,其中N为问题的维度,并且拟牛顿矩阵在最小点处与Hessian矩阵重合。 在这种幸福的一般非线性情况下,我们当然不会等待,但这至少有理由使我们不必过多担心初始矩阵的选择不当。
结论
所描述的构造拟牛顿法的方法并非唯一可行的方法。 至少,所描述的拟牛顿方法的发现者和许多后来的研究人员在完全不同的考虑基础上得出了相同的公式。 但是,有趣的是,一旦出现了某种拟牛顿法,很短的时间后就清楚地知道这是对一些非常容易解释的优化问题的解决方案。 在我看来,很明显可以为这种多样化的方法带来一些共同点,因为这为构建更好地考虑特定任务细节的其他方法提供了基础。 特别是,存在设计用于更新稀疏矩阵的准牛顿方法,其中尽可能少的元素受到更改的方法,还有许多其他方法将是一种幻想。
还应该注意的是,尽管变量度量方法的名称很广,但它们并不总是会导致构建矩阵,而矩阵实际上是度量,尽管它们会尽可能地做到这一点。
这通常不是一个大问题,但是想要保护自己免受可能的尴尬的人可能会采取与克服Newton方法类似问题的相同技巧-例如通过更改方向或应用Levenberg-Marquardt方案。的确,在这种情况下,选择信任区域的形式的问题将再次变得重要,但是在这里您必须选择较少的邪恶。解决该问题的另一种方法是使用线性搜索方法,以确保满足维持肯定性确定性的必要条件。沃尔夫的规则保证了这一条件的实现,而阿米霍和戈尔茨坦的规则则没有。从理论上讲,要确定一类问题,几乎不可能确定大量可能的拟牛顿方法中哪一种是最有效的。通常,在制定方法时,它们仅限于显示其在最小化二次函数中的有效性(顺便说一句,如果该方法在N次迭代中产生了精确的解决方案,则该方法被认为是有效的,也就是说,不比解决SLAE的直接方法慢得多)。在更罕见的情况下,人们可以研究该方法的收敛阶数(通常是超线性的,即明显优于梯度下降所给出的阶数),稳定性和其他感兴趣的特征。但是总的来说,判断特定方法对特定类别任务的有效性的唯一合理标准是实践。因此,铲在手-并成功应用。