🤘🏻 👨🏽‍🎓 🈲 CUDA上的Navier-Stokes方程和流体模拟 💃🏻 🙇🏿 🎻

哈Ha 在本文中，我们将处理不可压缩流体的Navier-Stokes方程，对其进行数值求解，并通过在CUDA上进行并行计算进行漂亮的模拟。主要目的是说明解决液体和气体建模问题时，如何在实践中应用方程式基础的数学。

警告

本文包含许多数学知识，因此对问题的技术方面有兴趣的人员可以直接转到算法的实现部分。但是，我仍然建议您阅读整篇文章，并尝试了解解决方案的原理。如果您在阅读结束时有任何问题，我将很乐意在帖子评论中回答。

注意：如果您正在通过移动设备阅读Habr，但没有看到公式，请使用网站的完整版本

不可压缩流体的Navier-Stokes方程

部 分 部 分 （ ）

${\部分{\ bf \ vec {u}} \ over {\部分t}} =-（{\ bf \ vec {u}} \ cdot \ nabla）{\ bf \ vec {u}}-{1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$

我认为至少每个人都听说过这个方程式，有些甚至可能是解析地解决了它的特殊情况，但总的来说，这个问题至今仍未解决。当然，在本文中我们没有设定解决千年问题的目标，但是我们仍然可以对其应用迭代方法。但是对于初学者来说，让我们看一下此公式中的表示法。

按照惯例，Navier-Stokes方程可分为五个部分：

$\部分{\ bf \ vec {u}} \ over \部分t$ -表示某一点的流体速度变化率（我们将在模拟中为每个粒子考虑该速度）。
$-（{\ bf \ vec {u}} \ cdot \ nabla）{\ bf \ vec {u}}$ -流体在太空中的运动。
$-{1 \ over \ rho} \ nabla {\ bf p}$ 施加在粒子上的压力是 $\ rho$ -流体密度系数）。
$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ -介质的粘度（越大，液体抵抗施加到其部分的力越强）， $\ nu$ -粘度系数）。
$\ bf \ vec {F}$ -我们对流体施加的外力（在我们的情况下，该力将起非常具体的作用-它将反映用户执行的操作。

另外，由于我们将考虑不可压缩且均质的流体，因此我们有另一个方程：

${{{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ 。环境中的能量是恒定的，不会流到任何地方，也不会来自任何地方。

剥夺所有对向量分析不熟悉的读者的想法是错误的，因此同时简短地浏览方程式中存在的所有运算符（但是，我强烈建议您回顾微分，微分和向量的含义，因为它们是所有这些的基础。什么将在下面讨论）。

我们从nabla运算符开始，该运算符就是这样的一个向量（在我们的例子中，它将是两部分的，因为我们将在二维空间中对流体进行建模）：

$\ nabla = {\开始{pmatrix} {\部分\ over \部分x}，{\部分\ over \部分y} \结束{pmatrix}}$

nabla运算符是矢量微分运算符，可以同时应用于标量函数和矢量一。在标量的情况下，我们获得函数的梯度（其偏导数的向量），在矢量的情况下，获得沿轴的偏导数之和。此运算符的主要功能是通过它可以表达矢量分析的主要操作- 梯度（梯度）， div （散度）， rot （转子）和

$\ nabla ^ 2$ （ Laplace运算符）。值得注意的是

$（{\ bf \ vec {u} \ cdot \ nabla}）{\ bf \ vec {u}}$ 不等于

$（{\ nabla \ cdot \ bf \ vec {u}}）{\ bf \ vec {u}}$ -nabla运算符不具有可交换性。

正如我们将在后面看到的那样，当移动到一个离散空间来执行所有计算时，这些表达式将显着简化，因此，如果您现在不太清楚如何处理所有这些，请不要惊慌。将任务划分为几个部分，我们将依次解决每个部分，并以将多个功能顺序应用到我们的环境中的形式呈现所有这些内容。

Navier-Stokes方程的数值解

为了在程序中表示流体，我们需要在任意时间点获得每个流体粒子状态的数学表示。最方便的方法是创建一个粒子矢量场，以坐标平面的形式存储其状态：

在二维数组的每个像元中，我们将一次存储粒子速度

$t：{\ bf \ vec {u}} = u（{\ bf \ vec {x}}，t），\ bf \ vec {x} = \开始{pmatrix} x，y \ end {pmatrix}$ ，粒子之间的距离用

$\增量x$ 和

$\增量$ 相应地。在代码中，对于我们来说，每次迭代更改速度值就足以解决一组几个方程式。

现在我们考虑到我们的坐标网格来表示梯度，散度和拉普拉斯算子（

$我，j$ -数组中的索引，

$\ bf \ vec {u} _ {（x）}，\ vec {u} _ {{y）}$ -从向量中获取相应的分量）：

操作员	定义	离散模拟
毕业	$\ nabla \ bf p = \开始{pmatrix} {\部分\ bf p \ over \部分x}，{\部分\ bf p \ over \部分y} \结束{pmatrix}$	${{p_ {i + 1，j}}-{p_ {i-1，j}} \ over {2 \ delta x}}，{{p_ {i，j + 1}}-{p_ {i， j-1}} \超过{2 \ delta y}}$
div	$\ nabla \ cdot \ bf \ vec {u} = {{\部分u \ over \部分x} + {\部分u \ over \部分y}}$	${{\\ vec {u} _ {（x）i + 1，j}-\ vec {u} _ {{x）i-1，j}} \ over {2 \ delta x}} + {{\ vec {u} _ {（y）i，j + 1}-\ vec {u} _ {{y）i，j-1}} \ over {2 \ delta y}}$
$\ bf \ Delta$	$\ bf \ nabla ^ 2p = {\部分^ 2 p \在\部分x ^ 2} + {\部分^ 2 p \在\部分y ^ 2}$	${{{p_ {i + 1，j} -2p_ {i，j} + p_ {i-1，j}} \ over（\ delta x）^ 2} + {{p_ {i，j + 1}- 2p_ {i，j} + p_ {i，j-1}} \ over（\ delta y）^ 2}$
腐烂	$\ bf \ nabla \ times \ vec {u} = {{\部分\ vec {u} \ over \部分y}-{\部分\ vec {u} \ over \部分x}}$	${\ vec {u} _ {（y）i，j + 1}-\ vec {u} _ {{y）i，j-1} \ over 2 \ delta y}-{\ vec {u} _ {{x i + 1，j}-\ vec {u} _ {{x i-1，j} \ over 2 \ delta x}$

如果我们假设向量运算符的离散公式可以进一步简化

$\ delta x = \ delta y = 1$ 。该假设不会极大地影响算法的准确性，但是，它减少了每次迭代的操作次数，并且通常使表达式更令人愉悦。

粒子运动

仅当我们可以找到相对于当前正在考虑的粒子最近的粒子时，这些语句才起作用。为了使与找到它们相关的所有可能成本无效，我们将不跟踪它们的运动，而是通过在时间上向后投影运动轨迹来跟踪粒子在迭代开始时的位置（换句话说，减去速度矢量乘以时间变化）当前位置）。对数组的每个元素使用此技术，我们将确保任何粒子都将具有“邻居”：

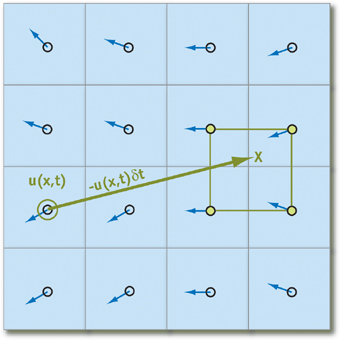
把那个

$q$ -存储粒子状态的数组元素，我们获得以下公式来计算粒子随时间的状态

$\增量t$ （我们认为，已经计算出了所有必需的参数，如加速度和压力）：

$q（{{\ vec {\ bf x}}，t + \ delta t}）= q（{{\ \ bf \ vec {x}}-{\ bf \ vec {u}} \ delta t}，t）$

我们立即注意到，对于足够小的

$\增量t$ 而且我们永远都不会超出细胞的限制，因此选择用户赋予颗粒合适的动量非常重要。

为了避免在投影碰到单元格边界或非整数坐标的情况下准确性下降，我们将对四个最近粒子的状态进行双线性插值，并将其作为该点的真实值。原则上，这种方法实际上不会降低仿真的准确性，同时实现起来也很简单，因此我们将使用它。

黏度

每种液体都有一定的粘度，可以防止外力对其零件产生影响（蜂蜜和水将是一个很好的例子，在某些情况下，它们的粘度系数相差一个数量级）。粘度直接影响液体获得的加速度，可以用下面的公式表示，如果为了简短起见，我们暂时省略了其他术语：

${\部分\ vec {\ bf u} \ over \部分t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$

。在这种情况下，速度的迭代方程采用以下形式：

$u（{\ bf \ vec {x}}，t + \ delta t）= u（{\ bf \ vec {x}}，t）+ \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$

我们将稍微改变这种平等，将其转化为形式

$\ bf A \ vec {x} = \ vec {b}$ （线性方程组的标准形式）：

$（{\ bf I}-\ nu \ delta t \ nabla ^ 2）u（{\ bf \ vec {x}}，t + \ delta t）= {u（{\ bf \ vec {x}}，t ）}$

在哪里

$\ bf I$ 是单位矩阵。我们需要进行这样的转换，以便随后应用Jacobi方法来求解几个相似的方程组。我们稍后还将讨论。

外力

该算法最简单的步骤是对介质施加外力。对于用户而言，这将以鼠标或其移动在屏幕上的单击形式反映出来。外力可以通过以下公式描述，我们将其应用于矩阵的每个元素（

$\ vec {\ bf G}$ -动量矢量

$x_p，y_p$ -鼠标位置

$x，y$ -当前单元格的坐标，

-作用半径，缩放参数）：

$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \左（-{{{（x-x_p）^ 2 +（y-y_p）^ 2} \ over r} \正确）$

可以将冲动矢量轻松地计算为鼠标的上一个位置与当前位置（如果有）之间的差，在这里您仍然可以发挥创造力。正是在算法的这一部分中，我们可以将颜色添加到液体，其照明等中。外力还可以包括重力和温度，尽管实现这些参数并不困难，但在本文中我们将不考虑它们。

压力值

Navier-Stokes方程中的压力是一种力，该力可防止在对粒子施加任何外力之后将粒子填满所有可用空间。立刻，它的计算非常困难，但是通过应用亥姆霍兹分解定理可以大大简化我们的问题。

致电

$\ bf \ vec {W}$ 计算位移，外力和粘度后获得的矢量场。它将具有非零散度，这与液体不可压缩的条件相矛盾（

$\ nabla \ cdot \ bf \ vec {u} = 0$ ），并且要解决此问题，必须计算压力。根据亥姆霍兹分解定理，

$\ bf \ vec {W}$ 可以表示为两个字段的总和：

$\ bf \ vec {W} = \ vec {u} + \ nabla p$

在哪里

$\ bf u$ -这是我们正在寻找零散度的向量场。本文不会提供这种相等性的证明，但是最后您可以找到带有详细说明的链接。我们可以将nabla运算符应用于表达式的两侧，以获得以下公式来计算标量压力场：

$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot（\ vec {u} + \ nabla p）= \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p$

上面写的表达式是压力的泊松方程。我们还可以通过前述的Jacobi方法求解它，从而在Navier-Stokes方程中找到最后一个未知变量。原则上，线性方程组可以用各种不同的复杂方法求解，但是我们将继续讨论它们中最简单的一个，以免给本文增加负担。

边界条件和初始条件

在有限域上建模的任何微分方程都需要正确指定初始或边界条件，否则我们很可能会得到物理上不正确的结果。建立边界条件以控制坐标网格边缘附近的流体行为，并且初始条件指定程序启动时粒子具有的参数。

初始条件将非常简单-最初流体是静止的（粒子速度为零），压力也为零。边界条件将通过给定公式设置速度和压力：

${\ bf \ vec {u} _ {0，j} + \ bf \ vec {u} _ {1，j} \ over 2 \ delta y} = 0，{\ bf \ vec {u} _ {i ，0} + \ bf \ vec {u} _ {i，1} \超过2 \ delta x} = 0$

${\ bf p_ {0，j}-\ bf p_ {1，j} \ over \ delta x} = 0，{\ bf p_ {i，0}-\ bf p_ {i，1} \ over \ delta y} = 0$

因此，边缘处的粒子速度将与边缘处的速度相反（因此它们将从边缘排斥），并且压力等于紧邻边界的值。这些操作应应用于数组的所有边界元素（例如，存在网格大小

$N \乘以M$ ，然后将算法应用于图中蓝色标记的单元）：

染剂

利用我们现在拥有的，您已经可以想出很多有趣的东西。例如，实现染料在液体中的扩散。为此，我们只需要维护另一个标量字段，该字段将负责模拟每个点上的绘制量。更新染料的公式与速度非常相似，表示为：

${\部分d \ over \部分t} = {-（\ vec {\ bf u} \ cdot \ nabla）d} + \ gamma \ nabla ^ 2d + S$

在公式中

$S$ 负责为该区域补充染料（可能取决于用户单击的位置），

$d$ 直接是该点的染料量，并且

$\伽玛$ -扩散系数。解决这个问题并不困难，因为有关公式推导的所有基本工作已经完成，并且足以进行一些替换。绘画可以在代码中以RGB格式的颜色实现，在这种情况下，任务可以简化为具有多个实际值的操作。

涡度

涡度方程不是Navier-Stokes方程的直接部分，但是对于合理地模拟染料在液体中的运动，它是一个重要的参数。由于我们正在离散的字段上生成算法，并且由于浮点值精度的损失，因此这种效果消失了，因此我们需要通过对空间中的每个点施加额外的力来恢复它。此力的向量指定为

$\ bf \ vec {T}$ 并由以下公式确定：

$\ bf \ omega = \ nabla \ times \ vec {u}$

$\ vec {\ eta} = \ nabla | \ omega |$

$\ bf \ vec {\ psi} = {\ vec {\ eta} \ over {| \ vec {\ eta} |}}$

$\ bf \ vec {T} = \ epsilon（\ vec {\ psi} \ times \ omega）\ delta x$

$\ omega$ 将转子应用于速度矢量的结果（在本文开头给出了其定义），

$\ vec \ eta$ -绝对值的标量场的梯度

$\ omega$ 。

$\ vec \ psi$ 代表归一化向量

$\ vec \ eta$ 和

$\ epsilon$ 是一个常数，用于控制流体中的涡旋大小。

求解线性方程组的Jacobi方法

在分析Navier-Stokes方程时，我们提出了两个方程组-一个用于粘度，另一个用于压力。它们可以通过迭代算法解决，该算法可以通过以下迭代公式来描述：

$x ^ {（k + 1）} _ {i，j} = {{x ^ {{k）} _ {i-1，j} + x ^ {{k）} _ {i + 1，j} + x ^ {{（k）} _ {i，j-1} + x ^ {{k）} _ {i，j + 1} + \ alpha b_ {i，j}} \ over \ beta}$

对于我们

$x$ -表示标量或矢量字段的数组元素。

$k$ -迭代次数，我们可以对其进行调整，以提高计算的准确性，反之亦然，以减少迭代次数并提高生产率。

为了计算粘度，我们用以下公式代替：

$x = b = \ bf \ vec {u}$ ，

$\ alpha = {1 \ over \ nu \ delt t}$ ，

$\ beta = 4+ \ alpha$ ，这是参数

$\ beta$ -权重之和。因此，我们需要存储至少两个矢量速度场，以便独立读取一个场的值并将其写入另一场。平均而言，为了通过Jacobi方法计算速度场，必须执行20至50次迭代，如果我们在CPU上进行计算，这将是很多工作。

对于压力方程，我们进行以下替换：

$x = p$ ，

$b = \ nabla \ bf \ cdot \ vec {W}$ ，

$\ alpha = -1$ ，

$\ beta = 4$ 。结果，我们获得了价值

$p_ {i，j} \ delta t$ 在这一点上。但是，由于它仅用于计算从速度场减去的梯度，因此可以省略其他变换。对于压力场，最好执行40-80次迭代，因为数字越小，差异就越明显。

算法实现

我们将使用C ++实现该算法，还需要Cuda Toolkit （您可以在Nvidia网站上阅读如何安装它）以及SFML 。我们需要CUDA来使算法并行化，并且SFML仅用于创建窗口并在屏幕上显示图片（原则上，这可以用OpenGL编写，但是性能上的差别并不明显，但是代码会再增加200行）。

Cuda工具包

首先，我们将讨论如何使用Cuda Toolkit并行化任务。 Nvidia本身提供了更详细的指南，因此在这里我们只限于最必要的内容。还假定您能够安装编译器，并且能够构建测试项目而没有错误。

要创建在GPU上运行的功能，您首先需要声明我们要使用多少个内核，以及要分配多少个内核块。为此，Cuda Toolkit为我们提供了一种特殊的结构-dim3 ，默认情况下将其所有x，y，z值都设置为1。通过在调用函数时将其指定为参数，我们可以控制分配的内核数。由于我们使用的是二维数组，因此我们只需要在构造函数中设置两个字段： x和y ：

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads);

其中size_x和size_y是要处理的数组的大小。签名和函数调用如下（三尖括号由Cuda编译器处理）：

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host

在函数本身中，可以使用以下公式通过该块中的块号和内核号来恢复二维数组的索引：

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y;

应当注意，在视频卡上执行的功能必须用__global__标记标记，并且必须返回void ，因此大多数情况下，计算结果将作为参数传递到数组中，并预先分配在视频卡的内存中。

功能CudaMalloc和CudaFree负责释放和分配视频卡上的内存。我们可以对指向它们返回的存储区的指针进行操作，但是我们无法从主代码访问数据。返回计算结果的最简单方法是使用cudaMemcpy ，类似于标准memcpy ，但是能够将数据从视频卡复制到主内存，反之亦然。

SFML和窗口渲染

有了所有这些知识，我们终于可以继续直接编写代码。首先，让我们创建main.cpp文件，并在其中放置窗口渲染的所有辅助代码：

main.cpp

 #include <SFML/Graphics.hpp> #include <chrono> #include <cstdlib> #include <cmath> //SFML REQUIRED TO LAUNCH THIS CODE #define SCALE 2 #define WINDOW_WIDTH 1280 #define WINDOW_HEIGHT 720 #define FIELD_WIDTH WINDOW_WIDTH / SCALE #define FIELD_HEIGHT WINDOW_HEIGHT / SCALE static struct Config { float velocityDiffusion; float pressure; float vorticity; float colorDiffusion; float densityDiffusion; float forceScale; float bloomIntense; int radius; bool bloomEnabled; } config; void setConfig(float vDiffusion = 0.8f, float pressure = 1.5f, float vorticity = 50.0f, float cDiffuion = 0.8f, float dDiffuion = 1.2f, float force = 1000.0f, float bloomIntense = 25000.0f, int radius = 100, bool bloom = true); void computeField(uint8_t* result, float dt, int x1pos = -1, int y1pos = -1, int x2pos = -1, int y2pos = -1, bool isPressed = false); void cudaInit(size_t xSize, size_t ySize); void cudaExit(); int main() { cudaInit(FIELD_WIDTH, FIELD_HEIGHT); srand(time(NULL)); sf::RenderWindow window(sf::VideoMode(WINDOW_WIDTH, WINDOW_HEIGHT), ""); auto start = std::chrono::system_clock::now(); auto end = std::chrono::system_clock::now(); sf::Texture texture; sf::Sprite sprite; std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); texture.create(FIELD_WIDTH, FIELD_HEIGHT); sf::Vector2i mpos1 = { -1, -1 }, mpos2 = { -1, -1 }; bool isPressed = false; bool isPaused = false; while (window.isOpen()) { end = std::chrono::system_clock::now(); std::chrono::duration<float> diff = end - start; window.setTitle("Fluid simulator " + std::to_string(int(1.0f / diff.count())) + " fps"); start = end; window.clear(sf::Color::White); sf::Event event; while (window.pollEvent(event)) { if (event.type == sf::Event::Closed) window.close(); if (event.type == sf::Event::MouseButtonPressed) { if (event.mouseButton.button == sf::Mouse::Button::Left) { mpos1 = { event.mouseButton.x, event.mouseButton.y }; mpos1 /= SCALE; isPressed = true; } else { isPaused = !isPaused; } } if (event.type == sf::Event::MouseButtonReleased) { isPressed = false; } if (event.type == sf::Event::MouseMoved) { std::swap(mpos1, mpos2); mpos2 = { event.mouseMove.x, event.mouseMove.y }; mpos2 /= SCALE; } } float dt = 0.02f; if (!isPaused) computeField(pixelBuffer.data(), dt, mpos1.x, mpos1.y, mpos2.x, mpos2.y, isPressed); texture.update(pixelBuffer.data()); sprite.setTexture(texture); sprite.setScale({ SCALE, SCALE }); window.draw(sprite); window.display(); } cudaExit(); return 0; }

主功能开头的行

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4);

创建具有恒定长度的一维数组形式的RGBA图像。我们将其与其他参数（鼠标位置，帧之间的差异）一起传递给computeField函数。后者以及其他几个函数在kernel.cu中声明，并调用在GPU上执行的代码。您可以在SFML网站上找到有关任何功能的文档，文件代码中没有任何有趣的事情，因此我们不会在此停留太久了。

GPU计算

要开始在gpu下编写代码，请首先创建一个kernel.cu文件并在其中定义几个辅助类： Color3f，Vec2，Config，SystemConfig ：

kernel.cu（数据结构）

 struct Vec2 { float x = 0.0, y = 0.0; __device__ Vec2 operator-(Vec2 other) { Vec2 res; res.x = this->x - other.x; res.y = this->y - other.y; return res; } __device__ Vec2 operator+(Vec2 other) { Vec2 res; res.x = this->x + other.x; res.y = this->y + other.y; return res; } __device__ Vec2 operator*(float d) { Vec2 res; res.x = this->x * d; res.y = this->y * d; return res; } }; struct Color3f { float R = 0.0f; float G = 0.0f; float B = 0.0f; __host__ __device__ Color3f operator+ (Color3f other) { Color3f res; res.R = this->R + other.R; res.G = this->G + other.G; res.B = this->B + other.B; return res; } __host__ __device__ Color3f operator* (float d) { Color3f res; res.R = this->R * d; res.G = this->G * d; res.B = this->B * d; return res; } }; struct Particle { Vec2 u; // velocity Color3f color; }; static struct Config { float velocityDiffusion; float pressure; float vorticity; float colorDiffusion; float densityDiffusion; float forceScale; float bloomIntense; int radius; bool bloomEnabled; } config; static struct SystemConfig { int velocityIterations = 20; int pressureIterations = 40; int xThreads = 64; int yThreads = 1; } sConfig; void setConfig( float vDiffusion = 0.8f, float pressure = 1.5f, float vorticity = 50.0f, float cDiffuion = 0.8f, float dDiffuion = 1.2f, float force = 5000.0f, float bloomIntense = 25000.0f, int radius = 500, bool bloom = true ) { config.velocityDiffusion = vDiffusion; config.pressure = pressure; config.vorticity = vorticity; config.colorDiffusion = cDiffuion; config.densityDiffusion = dDiffuion; config.forceScale = force; config.bloomIntense = bloomIntense; config.radius = radius; config.bloomEnabled = bloom; } static const int colorArraySize = 7; Color3f colorArray[colorArraySize]; static Particle* newField; static Particle* oldField; static uint8_t* colorField; static size_t xSize, ySize; static float* pressureOld; static float* pressureNew; static float* vorticityField; static Color3f currentColor; static float elapsedTime = 0.0f; static float timeSincePress = 0.0f; static float bloomIntense; int lastXpos = -1, lastYpos = -1;

方法名称前面的__host__属性意味着可以在CPU __device__上执行代码，相反，这迫使编译器必须在GPU下收集代码。该代码声明了用于与两个分量的矢量，颜色，具有可在运行时更改的参数的配置一起使用的原语，以及几个指向数组的静态指针，我们将它们用作计算的缓冲区。

cudaInit和cudaExit的定义也很简单：

kernel.cu（init）

 void cudaInit(size_t x, size_t y) { setConfig(); colorArray[0] = { 1.0f, 0.0f, 0.0f }; colorArray[1] = { 0.0f, 1.0f, 0.0f }; colorArray[2] = { 1.0f, 0.0f, 1.0f }; colorArray[3] = { 1.0f, 1.0f, 0.0f }; colorArray[4] = { 0.0f, 1.0f, 1.0f }; colorArray[5] = { 1.0f, 0.0f, 1.0f }; colorArray[6] = { 1.0f, 0.5f, 0.3f }; int idx = rand() % colorArraySize; currentColor = colorArray[idx]; xSize = x, ySize = y; cudaSetDevice(0); cudaMalloc(&colorField, xSize * ySize * 4 * sizeof(uint8_t)); cudaMalloc(&oldField, xSize * ySize * sizeof(Particle)); cudaMalloc(&newField, xSize * ySize * sizeof(Particle)); cudaMalloc(&pressureOld, xSize * ySize * sizeof(float)); cudaMalloc(&pressureNew, xSize * ySize * sizeof(float)); cudaMalloc(&vorticityField, xSize * ySize * sizeof(float)); } void cudaExit() { cudaFree(colorField); cudaFree(oldField); cudaFree(newField); cudaFree(pressureOld); cudaFree(pressureNew); cudaFree(vorticityField); }

在初始化函数中，我们为二维数组分配内存，指定将用于绘制液体的颜色数组，并在配置中设置默认值。在cudaExit中，我们只是释放所有缓冲区。听起来很矛盾，对于存储二维数组，使用一维数组是最有利的，将使用以下表达式进行访问：

 array[y * size_x + x]; // equals to array[y][x]

我们开始使用粒子运动函数来实现直接算法。字段oldField和newField （数据来自的字段以及将数据写入的字段），数组的大小以及时间增量和密度系数（用于加速染料在液体中的溶解并使介质对平移不太敏感）被转移到平移中用户操作）。双线性插值函数是通过计算中间值以经典方式实现的：

kernel.cu（建议）

 // interpolates quantity of grid cells __device__ Particle interpolate(Vec2 v, Particle* field, size_t xSize, size_t ySize) { float x1 = (int)vx; float y1 = (int)vy; float x2 = (int)vx + 1; float y2 = (int)vy + 1; Particle q1, q2, q3, q4; #define CLAMP(val, minv, maxv) min(maxv, max(minv, val)) #define SET(Q, x, y) Q = field[int(CLAMP(y, 0.0f, ySize - 1.0f)) * xSize + int(CLAMP(x, 0.0f, xSize - 1.0f))] SET(q1, x1, y1); SET(q2, x1, y2); SET(q3, x2, y1); SET(q4, x2, y2); #undef SET #undef CLAMP float t1 = (x2 - vx) / (x2 - x1); float t2 = (vx - x1) / (x2 - x1); Vec2 f1 = q1.u * t1 + q3.u * t2; Vec2 f2 = q2.u * t1 + q4.u * t2; Color3f C1 = q2.color * t1 + q4.color * t2; Color3f C2 = q2.color * t1 + q4.color * t2; float t3 = (y2 - vy) / (y2 - y1); float t4 = (vy - y1) / (y2 - y1); Particle res; res.u = f1 * t3 + f2 * t4; res.color = C1 * t3 + C2 * t4; return res; } // adds quantity to particles using bilinear interpolation __global__ void advect(Particle* newField, Particle* oldField, size_t xSize, size_t ySize, float dDiffusion, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float decay = 1.0f / (1.0f + dDiffusion * dt); Vec2 pos = { x * 1.0f, y * 1.0f }; Particle& Pold = oldField[y * xSize + x]; // find new particle tracing where it came from Particle p = interpolate(pos - Pold.u * dt, oldField, xSize, ySize); pu = pu * decay; p.color = p.color * decay; newField[y * xSize + x] = p; }

决定将粘度扩散函数分为几部分：从主代码调用computeDiffusion ，该函数将diffuse和computeColor调用预定的次数，然后从获取数据的位置交换数组并从写入数据的位置交换数组。这是实现并行数据处理的最简单方法，但是我们要花两倍的内存。

这两个函数都会导致Jacobi方法的变化。 jacobiColor和jacobiVelocity的主体会立即检查当前元素是否不在边界上-在这种情况下，我们必须根据“ 边界和初始条件”部分所述的公式进行设置。

kernel.cu（漫反射）

 // performs iteration of jacobi method on color grid field __device__ Color3f jacobiColor(Particle* colorField, size_t xSize, size_t ySize, Vec2 pos, Color3f B, float alpha, float beta) { Color3f xU, xD, xL, xR, res; int x = pos.x; int y = pos.y; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = colorField[int(y) * xSize + int(x)] SET(xU, x, y - 1).color; SET(xD, x, y + 1).color; SET(xL, x - 1, y).color; SET(xR, x + 1, y).color; #undef SET res = (xU + xD + xL + xR + B * alpha) * (1.0f / beta); return res; } // calculates color field diffusion __global__ void computeColor(Particle* newField, Particle* oldField, size_t xSize, size_t ySize, float cDiffusion, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Vec2 pos = { x * 1.0f, y * 1.0f }; Color3f c = oldField[y * xSize + x].color; float alpha = cDiffusion * cDiffusion / dt; float beta = 4.0f + alpha; // perfom one iteration of jacobi method (diffuse method should be called 20-50 times per cell) newField[y * xSize + x].color = jacobiColor(oldField, xSize, ySize, pos, c, alpha, beta); } // performs iteration of jacobi method on velocity grid field __device__ Vec2 jacobiVelocity(Particle* field, size_t xSize, size_t ySize, Vec2 v, Vec2 B, float alpha, float beta) { Vec2 vU = B * -1.0f, vD = B * -1.0f, vR = B * -1.0f, vL = B * -1.0f; #define SET(U, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) U = field[int(y) * xSize + int(x)].u SET(vU, vx, vy - 1); SET(vD, vx, vy + 1); SET(vL, vx - 1, vy); SET(vR, vx + 1, vy); #undef SET v = (vU + vD + vL + vR + B * alpha) * (1.0f / beta); return v; } // calculates nonzero divergency velocity field u __global__ void diffuse(Particle* newField, Particle* oldField, size_t xSize, size_t ySize, float vDiffusion, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Vec2 pos = { x * 1.0f, y * 1.0f }; Vec2 u = oldField[y * xSize + x].u; // perfoms one iteration of jacobi method (diffuse method should be called 20-50 times per cell) float alpha = vDiffusion * vDiffusion / dt; float beta = 4.0f + alpha; newField[y * xSize + x].u = jacobiVelocity(oldField, xSize, ySize, pos, u, alpha, beta); } // performs several iterations over velocity and color fields void computeDiffusion(dim3 numBlocks, dim3 threadsPerBlock, float dt) { // diffuse velocity and color for (int i = 0; i < sConfig.velocityIterations; i++) { diffuse<<<numBlocks, threadsPerBlock>>>(newField, oldField, xSize, ySize, config.velocityDiffusion, dt); computeColor<<<numBlocks, threadsPerBlock>>>(newField, oldField, xSize, ySize, config.colorDiffusion, dt); std::swap(newField, oldField); } }

外力的使用是通过单个函数applyForce实现的 ，该函数将鼠标的位置，染料的颜色以及作用半径作为参数。有了它的帮助，我们可以提高粒子的速度，并对它们进行绘制。兄弟指数使您可以使区域不太尖锐，同时在指定半径内也非常清晰。

kernel.cu（强制）

 // applies force and add color dye to the particle field __global__ void applyForce(Particle* field, size_t xSize, size_t ySize, Color3f color, Vec2 F, Vec2 pos, int r, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float e = expf((-(powf(x - pos.x, 2) + powf(y - pos.y, 2))) / r); Vec2 uF = F * dt * e; Particle& p = field[y * xSize + x]; pu = pu + uF; color = color * e + p.color; p.color.R = min(1.0f, color.R); p.color.G = min(1.0f, color.G); p.color.B = min(1.0f, color.B); }

涡度的计算已经是一个更加复杂的过程，因此我们在computeVorticity和applyVorticity中实现它，我们还注意到，对于它们，有必要定义两个这样的矢量运算符，例如curl （转子）和absGradient （绝对场值的梯度）。为了指定其他涡旋效应，我们乘以

$y$ 上的梯度向量的分量

$-1$ ，然后通过除以长度对其进行归一化（不要忘记检查向量是否为非零）：

kernel.cu（涡度）

 // computes curl of velocity field __device__ float curl(Particle* field, size_t xSize, size_t ySize, int x, int y) { Vec2 C = field[int(y) * xSize + int(x)].u; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] float x1 = -Cx, x2 = -Cx, y1 = -Cy, y2 = -Cy; SET(x1, x + 1, y).ux; SET(x2, x - 1, y).ux; SET(y1, x, y + 1).uy; SET(y2, x, y - 1).uy; #undef SET float res = ((y1 - y2) - (x1 - x2)) * 0.5f; return res; } // computes absolute value gradient of vorticity field __device__ Vec2 absGradient(float* field, size_t xSize, size_t ySize, int x, int y) { float C = field[int(y) * xSize + int(x)]; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] float x1 = C, x2 = C, y1 = C, y2 = C; SET(x1, x + 1, y); SET(x2, x - 1, y); SET(y1, x, y + 1); SET(y2, x, y - 1); #undef SET Vec2 res = { (abs(x1) - abs(x2)) * 0.5f, (abs(y1) - abs(y2)) * 0.5f }; return res; } // computes vorticity field which should be passed to applyVorticity function __global__ void computeVorticity(float* vField, Particle* field, size_t xSize, size_t ySize) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; vField[y * xSize + x] = curl(field, xSize, ySize, x, y); } // applies vorticity to velocity field __global__ void applyVorticity(Particle* newField, Particle* oldField, float* vField, size_t xSize, size_t ySize, float vorticity, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Particle& pOld = oldField[y * xSize + x]; Particle& pNew = newField[y * xSize + x]; Vec2 v = absGradient(vField, xSize, ySize, x, y); vy *= -1.0f; float length = sqrtf(vx * vx + vy * vy) + 1e-5f; Vec2 vNorm = v * (1.0f / length); Vec2 vF = vNorm * vField[y * xSize + x] * vorticity; pNew = pOld; pNew.u = pNew.u + vF * dt; }

该算法的下一步将是计算标量压力场及其在速度场上的投影。为此，我们需要实现4个功能： divergence （将考虑速度差异）， jacobiPressure （实现用于压力的Jacobi方法）以及带有computePressureImpl的computePressure （执行迭代字段计算）：

kernel.cu（压力）

 // performs iteration of jacobi method on pressure grid field __device__ float jacobiPressure(float* pressureField, size_t xSize, size_t ySize, int x, int y, float B, float alpha, float beta) { float C = pressureField[int(y) * xSize + int(x)]; float xU = C, xD = C, xL = C, xR = C; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = pressureField[int(y) * xSize + int(x)] SET(xU, x, y - 1); SET(xD, x, y + 1); SET(xL, x - 1, y); SET(xR, x + 1, y); #undef SET float pressure = (xU + xD + xL + xR + alpha * B) * (1.0f / beta); return pressure; } // computes divergency of velocity field __device__ float divergency(Particle* field, size_t xSize, size_t ySize, int x, int y) { Particle& C = field[int(y) * xSize + int(x)]; float x1 = -1 * Cux, x2 = -1 * Cux, y1 = -1 * Cuy, y2 = -1 * Cuy; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] SET(x1, x + 1, y).ux; SET(x2, x - 1, y).ux; SET(y1, x, y + 1).uy; SET(y2, x, y - 1).uy; #undef SET return (x1 - x2 + y1 - y2) * 0.5f; } // performs iteration of jacobi method on pressure field __global__ void computePressureImpl(Particle* field, size_t xSize, size_t ySize, float* pNew, float* pOld, float pressure, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float div = divergency(field, xSize, ySize, x, y); float alpha = -1.0f * pressure * pressure; float beta = 4.0; pNew[y * xSize + x] = jacobiPressure(pOld, xSize, ySize, x, y, div, alpha, beta); } // performs several iterations over pressure field void computePressure(dim3 numBlocks, dim3 threadsPerBlock, float dt) { for (int i = 0; i < sConfig.pressureIterations; i++) { computePressureImpl<<<numBlocks, threadsPerBlock>>>(oldField, xSize, ySize, pressureNew, pressureOld, config.pressure, dt); std::swap(pressureOld, pressureNew); } }

投影适合两个小功能- 投影和需要压力的渐变。这可以说是我们仿真算法的最后阶段：

kernel.cu（项目）

 // computes gradient of pressure field __device__ Vec2 gradient(float* field, size_t xSize, size_t ySize, int x, int y) { float C = field[y * xSize + x]; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] float x1 = C, x2 = C, y1 = C, y2 = C; SET(x1, x + 1, y); SET(x2, x - 1, y); SET(y1, x, y + 1); SET(y2, x, y - 1); #undef SET Vec2 res = { (x1 - x2) * 0.5f, (y1 - y2) * 0.5f }; return res; } // projects pressure field on velocity field __global__ void project(Particle* newField, size_t xSize, size_t ySize, float* pField) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Vec2& u = newField[y * xSize + x].u; u = u - gradient(pField, xSize, ySize, x, y); }

投影之后，我们可以安全地将图像渲染到缓冲区和各种后效果。绘制功能将颜色从粒子场复制到RGBA阵列。此外，还实现了applyBloom函数，当将光标置于其上并按下鼠标按钮时，该函数会突出显示液体。从经验来看，这种技术使图片对于用户的眼睛来说更加愉悦和有趣，但是根本没有必要。

在后期处理中，您还可以突出显示流体速度最快的位置，根据运动矢量更改颜色，添加各种效果等，但是在我们的情况下，我们将自身限制在最低限度，因为即使这样，图像也非常迷人（尤其是动态变化）：

kernel.cu（绘画）

 // adds flashlight effect near the mouse position __global__ void applyBloom(uint8_t* colorField, size_t xSize, size_t ySize, int xpos, int ypos, float bloomIntense) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; int pos = 4 * (y * xSize + x); float e = expf(-(powf(x - xpos, 2) + powf(y - ypos, 2)) * (1.0f / (bloomIntense + 1e-5f))); uint8_t R = colorField[pos + 0]; uint8_t G = colorField[pos + 1]; uint8_t B = colorField[pos + 2]; uint8_t maxval = max(R, max(G, B)); colorField[pos + 0] = min(255.0f, R + maxval * e); colorField[pos + 1] = min(255.0f, G + maxval * e); colorField[pos + 2] = min(255.0f, B + maxval * e); } // fills output image with corresponding color __global__ void paint(uint8_t* colorField, Particle* field, size_t xSize, size_t ySize) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float R = field[y * xSize + x].color.R; float G = field[y * xSize + x].color.G; float B = field[y * xSize + x].color.B; colorField[4 * (y * xSize + x) + 0] = min(255.0f, 255.0f * R); colorField[4 * (y * xSize + x) + 1] = min(255.0f, 255.0f * G); colorField[4 * (y * xSize + x) + 2] = min(255.0f, 255.0f * B); colorField[4 * (y * xSize + x) + 3] = 255; }

最后，我们还有一个主要函数，可以从main.cpp - computeField调用。它将算法的所有部分链接在一起，调用视频卡上的代码，还将数据从gpu复制到cpu。它还包含动量矢量的计算和染料颜色的选择，我们将其传递给applyForce ：

kernel.cu（主要功能）

 // main function, calls vorticity -> diffusion -> force -> pressure -> project -> advect -> paint -> bloom void computeField(uint8_t* result, float dt, int x1pos, int y1pos, int x2pos, int y2pos, bool isPressed) { dim3 threadsPerBlock(sConfig.xThreads, sConfig.yThreads); dim3 numBlocks(xSize / threadsPerBlock.x, ySize / threadsPerBlock.y); // curls and vortisity computeVorticity<<<numBlocks, threadsPerBlock>>>(vorticityField, oldField, xSize, ySize); applyVorticity<<<numBlocks, threadsPerBlock>>>(newField, oldField, vorticityField, xSize, ySize, config.vorticity, dt); std::swap(oldField, newField); // diffuse velocity and color computeDiffusion(numBlocks, threadsPerBlock, dt); // apply force if (isPressed) { timeSincePress = 0.0f; elapsedTime += dt; // apply gradient to color int roundT = int(elapsedTime) % colorArraySize; int ceilT = int((elapsedTime) + 1) % colorArraySize; float w = elapsedTime - int(elapsedTime); currentColor = colorArray[roundT] * (1 - w) + colorArray[ceilT] * w; Vec2 F; float scale = config.forceScale; Fx = (x2pos - x1pos) * scale; Fy = (y2pos - y1pos) * scale; Vec2 pos = { x2pos * 1.0f, y2pos * 1.0f }; applyForce<<<numBlocks, threadsPerBlock>>>(oldField, xSize, ySize, currentColor, F, pos, config.radius, dt); } else { timeSincePress += dt; } // compute pressure computePressure(numBlocks, threadsPerBlock, dt); // project project<<<numBlocks, threadsPerBlock>>>(oldField, xSize, ySize, pressureOld); cudaMemset(pressureOld, 0, xSize * ySize * sizeof(float)); // advect advect<<<numBlocks, threadsPerBlock>>>(newField, oldField, xSize, ySize, config.densityDiffusion, dt); std::swap(newField, oldField); // paint image paint<<<numBlocks, threadsPerBlock>>>(colorField, oldField, xSize, ySize); // apply bloom in mouse pos if (config.bloomEnabled && timeSincePress < 5.0f) { applyBloom<<<numBlocks, threadsPerBlock>>>(colorField, xSize, ySize, x2pos, y2pos, config.bloomIntense / timeSincePress); } // copy image to cpu size_t size = xSize * ySize * 4 * sizeof(uint8_t); cudaMemcpy(result, colorField, size, cudaMemcpyDeviceToHost); cudaError_t error = cudaGetLastError(); if (error != cudaSuccess) { std::cout << cudaGetErrorName(error) << std::endl; } }

结论

在本文中，我们分析了用于求解Navier-Stokes方程的数值算法，并为不可压缩的流体编写了一个小型仿真程序。也许我们并不了解所有的复杂性，但我希望该材料对您来说有趣而有用，至少可以作为流体建模领域的一个很好的介绍。

作为本文的作者，我将衷心感谢您的任何评论和补充，并将尝试回答您在本文下的所有问题。

附加材料

您可以在我的Github存储库中找到本文中的所有源代码。欢迎提出任何改进建议。

您可以在Nvidia的官方网站上阅读用作本文基础的原始材料。它还提供了用着色器语言实现算法各部分的示例：
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

本书中可以找到亥姆霍兹分解定理的证明以及有关流体力学的大量其他材料（英语，请参见第1.2节）：
Chorin，AJ和JE Marsden。 1993年。《流体力学数学导论》。 第三版。 施普林格

一个讲英语的YouTube的频道，制作与数学相关的高质量内容，尤其是求解微分方程（英语）。以帮助十分生动的视频，你明白很多事情在数学和物理学的本质：
3Blue1Brown - YouTube的
微分方程（3Blue1Brown）

也感谢WhiteBlackGoose在准备材料本文援助。

最后，还有一点好处-在程序中拍摄了一些漂亮的屏幕截图：