你好
当然，每个人都偶然看到了孩子与父母的相似程度的窥视孔评估：类似于“浇灌的父亲，但他看起来也像妈妈一样！”
（
取自此处 ）
就像图像中的示例一样，您可以用百分比来评估相似度。 您还可以使用亲戚以亲戚的亲戚加权总和的形式更准确地描述婴儿的脸...
对于与人类学或法医学无关的“普通”人，它将看起来自然而然。 对于分析和面部识别领域的专业人员而言，人脸更可能是一组参数。 即，以基准（与参数相对应的轴）为基准的某个空间中的点（一组坐标）。 而且，如果我们将孩子的面孔与其亲戚进行比较来描述，那么与孩子的面孔相对应的点很可能会出现在与亲属的下一个面孔相对应的点的凸包内部的参数空间中（但这是不准确的）。
实际上，我的全部意思是...描述脸部的这两种方法对应于两个坐标系：
- 重心，通过其他点的加权混合来描述空间中的一个点（在我们的示例中为面部）；
- 仿射，通过某种坐标对空间中的点进行描述。
那么什么是重心坐标？
进来
给定的三维空间
点
具有半径向量
，
。 此外，这些点都不位于其余点的半径向量的线性壳中。简单地说，这很简单：让这些点形成一个图形，无法在尺寸小于
。
在一维空间（线）的情况下，我们需要2个非重合点，在二维空间的情况下-一个非退化的三角形，在三维情况下-一个四面体。
那么空间中的任何一点
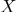
可以用半径向量表示
：
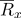
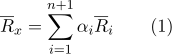
设置
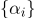
并且有重心坐标。
重心坐标比仿射更好/更差吗？
让我们从相对的缺点开始：
- 在重心表示中，我们需要比在仿射中更多的坐标。
- 在这些坐标中不能直接计算重心指定的点之间的距离。
尽管有必要使用
描述点中的重心坐标
-尺寸空间，度数不增加。 公式（1）中定义的重心坐标与以下关系相关：
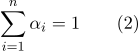
至于第二个缺点，如果需要计算重心表示的点之间的距离，那么计算标量积是有意义的
并使用马氏距离的类似物。
使用重心坐标有什么好处？
- 重心坐标对于空间的仿射变换是不变的。 例如，此属性用于计算机图形中的线性插值。 让纹理坐标定义在三角形表面元素的顶点处
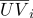和法线 
（ 
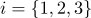），则此曲面截面的每个点将具有重心坐标 
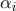它的纹理坐标 
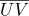和正常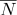 
可以计算为：
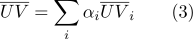
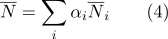
- 通过重心坐标，很容易确定一个点是否属于 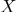由具有顶点的多面体界定的空间部分 ：只有在以下情况下才能这样做
。 第i个重心坐标1的相等意味着该点 
符合 。 如果多个重心坐标等于0，则这意味着该点属于一个子空间，该子空间由其对应坐标大于0的其余点的半径向量跨越。
也许它们很难计算？
没有比坐标系的任何线性变换更复杂的了。 因为从本质上讲，重心坐标的计算就是这样的变换。
我们以以下形式重写点的半径向量：
在哪里
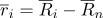
-坐标系统中以点为中心的径向矢量
。
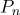
然后可以用以下形式重写公式（1）：
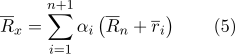
我们将在总和中显示方括号：
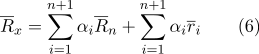
根据属性（2）：
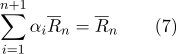
因此：
，
在哪里
给定（2），我们将自己限制为计算前n个重心坐标。 想象一下到重心坐标的转换是线性转换：
，
在哪里
-重心坐标的向量n（最后一个除外），
-转换矩阵。
给定重心表示的属性，如果为
替代向量之一
（
），那么我们得到一个零分量的向量，除了第i个第i个分量之外，它等于1。
如果矩阵
乘以矩阵
由以下各列组成
，那么我们应该获得恒等矩阵（主对角线为1，其余元素为零的矩阵）：
，
在哪里
，
是单位矩阵（
-克罗内克（Kronecker）符号：1，如果
否则为0）。
从（10）中我们发现
：
因此，具有一组带有半径向量的点
，
我们可以计算矩阵以转换为重心坐标：
使用这个矩阵，我们可以获得第一个
重心点坐标
半径矢量
：
再次使用关系式（2），我们获得最后一个重心坐标：
结论
乍一看，重心似乎也很尴尬和复杂。 但是实际上，这在许多任务中是非常方便且必不可少的工具，您很快就会习惯。 因为这里没有魔术，所以它是最纯形式的线性代数！