线性回归和梯度下降

让我们在某个主题领域研究具有定量表达方式的X和Y指标。

此外，有充分的理由相信指标Y取决于指标X。该位置既可以是科学假设，也可以基于基本常识。 例如，去杂货店。

表示方式：

X-销售区域（平方米）

Y-年营业额（百万页）

显然，交易区域越高，年营业额就越高（我们假设为线性关系）。

想象一下，我们有n个商店（零售空间和年营业额）的数据-我们的数据集和k个零售空间（X），我们要预测其年营业额（Y）-我们的任务。

我们假设Y的值取决于以下形式的X：Y = a + b * X

为了解决我们的问题，我们必须选择系数a和b。

首先，让我们设置a和b随机值。 之后，我们需要确定损失函数和优化算法。

为此，我们可以使用均方根损失函数（ MSELoss ）。 它由以下公式计算：



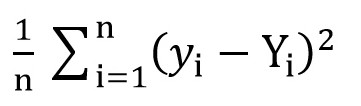
其中，在a = rand（）和b = rand（）之后，y [i] = a + b * x [i]，而Y [i]是x [i]的正确值。
在这一阶段，我们有了标准偏差（a和b的特定函数）。 很明显，此函数的值越小，相对于描述零售空间面积与该房间营业额之间确切关系的那些参数，选择的参数a和b越精确。

现在我们可以开始使用梯度下降（只是为了最小化损失函数）。

梯度下降

其本质非常简单。 例如，我们有一个函数：

y = x*x + 4 * x + 3 

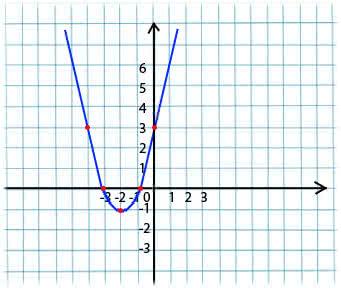
我们从函数定义的域中取x的任意值。 想象一下，这就是点x1 = -4。

接下来，我们在点x1处获取此函数相对于x的导数（如果函数取决于多个变量（例如a和b），则需要为每个变量取偏导数）。 y'（x1）= -4 <0

现在我们得到x的新值：x2 = x1-lr * y'（x1）。 lr（学习率）参数允许您设置步长。 这样我们得到：

如果给定点x1 <0的偏导数（函数减小），则我们移至局部最小值的点。 （x2将大于x1）

如果在给定点x1> 0处的偏导数（函数增加），那么我们仍将移至局部最小值的点。 （x2将小于x1）

通过迭代执行此算法，我们将达到最小值（但不会达到最小值）。

实际上，这一切看起来都简单得多（但是，我不敢说哪个系数a和b最适合上述商店的情况，因此我们采用y = 1 + 2 * x的形式来生成数据集，然后在此数据集）：
（代码写在这里 ）

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

编译代码后，您可以看到a和b的初始值分别与所需的1和2相距甚远，而最终值非常接近。

我将澄清为什么使用a_grad和b_grad的方式。
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) 。 F关于a的偏导数将是-2 * (1 + 2 * x_train – a + b * x_train) = -2 * error 。 F关于b的偏导数将是-2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error 。 我们取平均值(mean())因为error和x_train和y_train是值的数组，a和b是标量。

本文中使用的材料：

向datascience.com/了解pytorch的一个示例，逐步指导81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html