变异推理-它是什么，它吃什么？

哈Ha！

最近，我与同事谈论了一种变分自动编码器，结果发现即使是深度学习领域的许多人也知道变分推理（变数推理），尤其是仅通过传闻就知道了下变分界，而并不完全了解它是什么。
在本文中，我想详细分析这些问题。 谁在乎，我要求削减-这将非常有趣。

什么是变分推理？

机器学习的变分方法家族在数学分析“变分微积分”部分得名。 在本节中，我们研究搜索功能极值的问题（功能是功能的功能-也就是说，我们不是在寻找功能达到其最大值（最小）的变量的值，而是在功能达到最大值（最小）的函数。

但是出现了一个问题-在机器学习中，我们总是在参数（变量）空间中寻找一个点，其中损失函数具有最小值。 也就是说，这是经典数学分析的任务，这是变化的微积分吗？ 当我们使用变异微积分方法将损失函数转换为另一个损失函数（通常是较低的变异边界）时，就会出现变异微积分。

我们为什么需要这个？ 不能直接优化损失函数吗？ 当不可能直接获得无偏梯度估计（或者该估计具有很高的离散度）时，我们需要这些方法。 例如，我们的模型集 $$$p（z）$ 和 $$$p（x / z）$ ，我们需要计算 $$$p（x）= \ int（p（z）p（x / z）dz）$ 。 这正是变分自动编码器的设计目标。

什么是变化下界？

想象我们有一个功能 $$$f（x）$ 。 此函数的下限将是任何函数 $$$g（x）$ 满足方程式：

$$

$$g（x）<= f（x）$$

也就是说，对于任何函数，都有无数的下限。 所有这些下限都一样吗？ 当然不是 我们引入了另一个概念-差异（我在俄语文学中没有找到一个固定的术语，在英语文章中，这个值称为紧密度）：

$$

$$\ delta = max {f（x）}-max {g（x）}$$

显然，残差始终为正。 残留量越小越好。

以下是零残差的下限示例：

这是一个带有少量但为正的残差的示例：

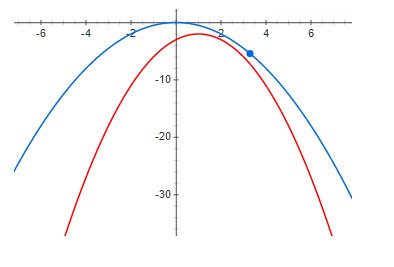
最后，足够大的差异：


从上面的图中可以清楚地看到，在零残差时，函数的最大值和下边界的最大值在同一点。 也就是说，如果我们想找到某个函数的最大值，则可以搜索下边界的最大值。 如果差异不为零，则事实并非如此。 并且下边界的最大值可能与所需最大值相距很远（沿x轴）。 这些图表明，残差越大，高点彼此之间的距离就越远。 这通常是不正确的，但是在大多数实际情况下，这种直觉效果很好。

可变自动编码器

现在，我们将分析一个示例，该示例具有一个很好的较低的变分边界，其残差可能为零（下面将清楚说明为什么）-这是一个变分自动编码器。

我们的任务是建立一个生成模型并使用最大似然法对其进行训练。 该模型将具有以下形式：

$$

$$q（x）= \ int {q（z）q_ \ theta（x | z）dz}$$

在哪里 $$$q（x）$ 是生成的样本的概率密度， $$$z$ -潜在变量， $$$q（z）$ -潜在变量的概率密度（通常是一个简单的变量-例如，期望值为零且单位色散为零的多维高斯分布-通常，我们可以轻松地从中进行采样）， $$$q_ \ theta（x | z）$ -对于给定潜变量值的条件样本密度，在变分自动编码器中，选择了具有mat期望和离散度取决于z的高斯样本。

为什么我们需要以这种复杂的方式表示数据密度？ 答案很简单-数据具有非常复杂的密度函数，我们根本无法从技术上直接构建这种密度的模型。 我们希望可以使用两个简单的密度很好地近似此复杂密度。 $$$q（z）$ 和 $$$q_ \ theta（x | z）$ 。

我们要最大化以下功能：

$$

$$I = \ int {p（x）log（q（x））dx}$$

在哪里 $$$p（x）$ -数据概率密度。 主要问题是密度 $$$q（x）$ （具有足够灵活的模型），不可能进行分析性展示，并因此无法训练模型。

我们使用贝叶斯公式并按如下所示重写函数：

$$

$$I = \ int {p（x）log（\ frac {q（z）q（x | z）} {q（z | x）}）dx}$$

不幸的是 $$$q（z / x）$ 一切也很难计算（不可能通过积分进行分析）。 但是首先，我们注意到对数下的表达式不依赖于z，因此我们可以从任何分布的z对数取数学期望，并且不会改变函数的值，而是将对数乘以并除以相同的分布（通常我们只有一个条件-这种分布不应消失在任何地方）。 结果，我们得到：

$$

$$I = \ int {p（x）dx \ int {\ phi（z | x）log（\ frac {q（z）q（x | z）} {\ phi（z | x）}}}}} + \ int {p（x）dx \ int {\ phi（z | x）log（\ frac {\ phi（z | x）} {q（z | x）}）}}$$

请注意，首先，第二项是KL散度（这意味着它始终为正）：

$$

$$I = \ int {p（x）dx \ int {\ phi（z | x）log（\ frac {q（z）q（x | z）} {\ phi（z | x）}}}}} + \ int {p（x）KL [\ phi（z | x）|| q（z | x））] dx}$$

其次 $$$我$ 不依赖 $$$q（z | x）$ 不是来自 $$$\ phi（z | x）$ 。 因此，

$$

$$I> = \ int {p（x）dx \ int {\ phi（z | x）log（\ frac {q（z）q（x | z）} {\ phi（z | x）}}}} = VLB$$

在哪里 $$$磅$ -下变化边界（可变下界），并在以下情况达到最大值 $$$KL [\ phi（z | x）|| q（z | x））] = 0$ -即分布是相同的。

当且仅当分布符合KL散度时，正性和相等性才为零，这是通过变分方法精确地证明的，因此命名为变分边界。

我想指出的是，使用变化下限具有几个优点。 首先，它为我们提供了通过梯度方法优化损失函数的机会（尝试在不解析积分的情况下做到这一点），其次，它使逆分布近似 $$$q（z | x）$ 分布 $$$\ phi（z | x）$ -也就是说，我们不仅可以采样数据，还可以采样潜在变量。 不幸的是，主要缺点是当逆分布模型不灵活时，即当家庭 $$$\ phi（z | x）$ 不包含 $$$q（z | x）$ -残差将为正且等于：

$$

$$\ delta = \ int {p（x）\ underset {\ phi（z | x）} {min}（KL [\ phi（z | x）|| q（z | x）]）dx}$$

这意味着下边界的最大值和损失函数很可能不一致。 顺便说一句，用于生成图像的可变自动编码器生成的图像太模糊，我认为这仅仅是因为选择了一个太贫穷的家庭 $$$\ phi（z | x）$ 。

一个不太好的底线的例子

现在我们来看一个例子，一方面，下边界具有所有良好的属性（使用足够灵活的模型，残差将为零），但是与使用原始损失函数相比，它没有任何优势。 我相信这个示例非常有启发性，如果您不进行理论分析，则可以花费大量时间尝试训练没有意义的模型。 相反，模型很有意义，但是如果我们可以训练这样的模型，那么选择起来就容易了 $$$q（x）$ 来自同一个家庭，并直接使用最大可能性原则。

因此，我们将考虑与变分自动编码器完全相同的生成模型：

$$

$$q（x）= \ int {q（z）q_ \ theta（x | z）dz}$$

我们将使用相同的最大似然法进行训练：

$$

$$I = \ int {p（x）log（q（x））dx}$$

我们仍然希望 $$$q（x | z）$ 比这更“容易” $$$q（x）$ 。
只有现在我们会写 $$$我$ 有点不同：

$$

$$I = \ int {p（x）log（\ int {q（z）q_ \ theta（x | z）dz}）dx}$$

使用詹森公式，我们得到：

$$

$$I> = \ int {p（x）q（z）log（q_ \ theta（x | z））dxdz} = VLB$$

正是在这一刻，大多数人都在回答，而没有想到这确实是底线，您可以训练模型。 的确如此，但让我们看一下差异：

$$

$$\ delta = \ int {p（x）log（q（x））dx}-\ int {p（x）q（z）log（q_ \ theta（x | z））dxdz}$$

在哪里（通过两次应用贝叶斯公式）：

$$

$$\ delta = \ int {p（x）q（z）log（\ frac {q（x）} {q（x | z）}）dxdz} = \ int {p（x）q（z）log（ \ frac {q（z）} {q（z | x）}）dxdz}$$

很容易看到：

$$

$$\ delta = \ int {p（x）KL [q（z）|| q（z | x）] dx}$$

让我们看看如果增加下边界会发生什么-残差会减少。 使用相当灵活的模型：

$$

$$KL [q（z）|| q（z | x）] \ rightarrow0$$

一切似乎都很好-下边界的残差可能为零，并且模型相当灵活 $$$q（x | z）$ 一切都应该工作。 是的，这是真的，只有细心的读者才能注意到，当 $$$x$ 和 $$$z$ 是独立的随机变量！ 为了取得良好的结果，分配的“复杂性” $$$q（x | z）$ 应该不小于 $$$q（x）$ 。 也就是说，下边界没有给我们任何好处。

结论

较低的变分边界是一种出色的数学工具，可让您大致优化学习的“不便”功能。 但是，像任何其他工具一样，您需要非常了解它的优缺点，并且也必须非常小心地使用它。 我们考虑了一个很好的例子-变分自动编码器，以及下边界不是很好的例子，而如果不进行详细的数学分析，很难发现下边界的问题。

我希望至少是有用和有趣的。