计算素数和优化蛮力除数的公式

问候！ 我决定在闲暇时研究寻找素数的问题。 这个话题是广泛而有趣的。 我想就此发表一些想法。 互联网上的搜索没有发现这种现象，这表明它们的独创性。

首先，我从未找到用于计算阶数的数学公式。 但是毕竟，如果有算法，那么当然可以使用逻辑函数或运算符来组成公式。 我在下面给出最简洁的公式。

对于一些数字序列 $$$（x_ {m}）= {x_ {1}，x_ {2}，x_ {3}，... x_ {max}}$ 我们介绍了检测等于a的第一个数字的运算符：

$$

$$\ mathbf {Dt_ {a}}（x_ {m}）：= \左\ {\开始{矩阵} m \ \ mathbf {if} \ \存在\ m：\ forall \，k <m \ x_ {k } \ neq a \ \ mathbf {and} \ x_ {m} = a \\ 0 \ \ mathbf {否则} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \末尾{矩阵} \对$$

从5开始的所有素数都可以通过以下公式计算：

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt {0} ^ {i}}（\ mathbf {Dt {0} ^ {j}}（（P_ {n-1} + 2i） \，mod \，P_ {j + 1}）），\ \ \ \ forall \，n \ geqslant 3 \\ \ forall \，i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ \ alpha -1}} {2} +10 \ ,, \ \ 2 \ leqslant \ alpha \ leqslant n-1; \ \ j_ {max} = \ pi（\ sqrt {P_ {n-1} + 2i}）-1$$

操作员 $$$\ mathbf {Dt_ {0} ^ {j}}$ 遍历 $$$j$ 将每个候选数除以简单的余数 $$$我$ 数 $$$（P_ {n-1} + 2i）$ 至已经找到的素数 $$$P_ {j_ {max} +1}$ 。 从大于前一个质数的奇数中按顺序选择候选数 $$$P_ {n-1}$ 。 $$$\ pi（\ sqrt {P_ {n-1} + 2i}）$ 是pi函数，显示素数 $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ 。
操作员 $$$\ mathbf {Dt_ {0} ^ {i}}$ 遍历 $$$我$ 操作员输出值 $$$\ mathbf {Dt_ {0} ^ {j}}$ 直到找到0。由于素数级数是无限的，所以这迟早会发生。 在操作员出口处 $$$\ mathbf {Dt_ {0} ^ {i}}$ 所以总会有一些数字 $$$我$ 。 下界 $$$i_ {max}$ 由相邻质数的最大差小于所需的质数确定。 这种差异的增加是对数的。 下图显示了最大和平均增长率的依赖性 $$$\ Delta P _ {\ alpha}$ 从n开始的前100,000个素数。 对最大值进行采样，并对每千个数字取平均值。
质数差的最大增加 $$$\ delta _ {max}（\ Delta P _ {\ alpha}）$ 到以前的最大值 $$$max（\ Delta P _ {\ alpha}）$ 等于20（素数之差31397-31469 = 72相对之差25523-25471 = 52）。 它是包络对数的导数的区域 $$$\ Delta P _ {\ alpha}$ 仍然足够大，素数不再太小。 根据此值， $$$i_ {max}$ 。 图表 $$$\ delta _ {max}（\ Delta P _ {\ alpha}）$ 下面给出的前50,000个素数。 每千计算一次值。
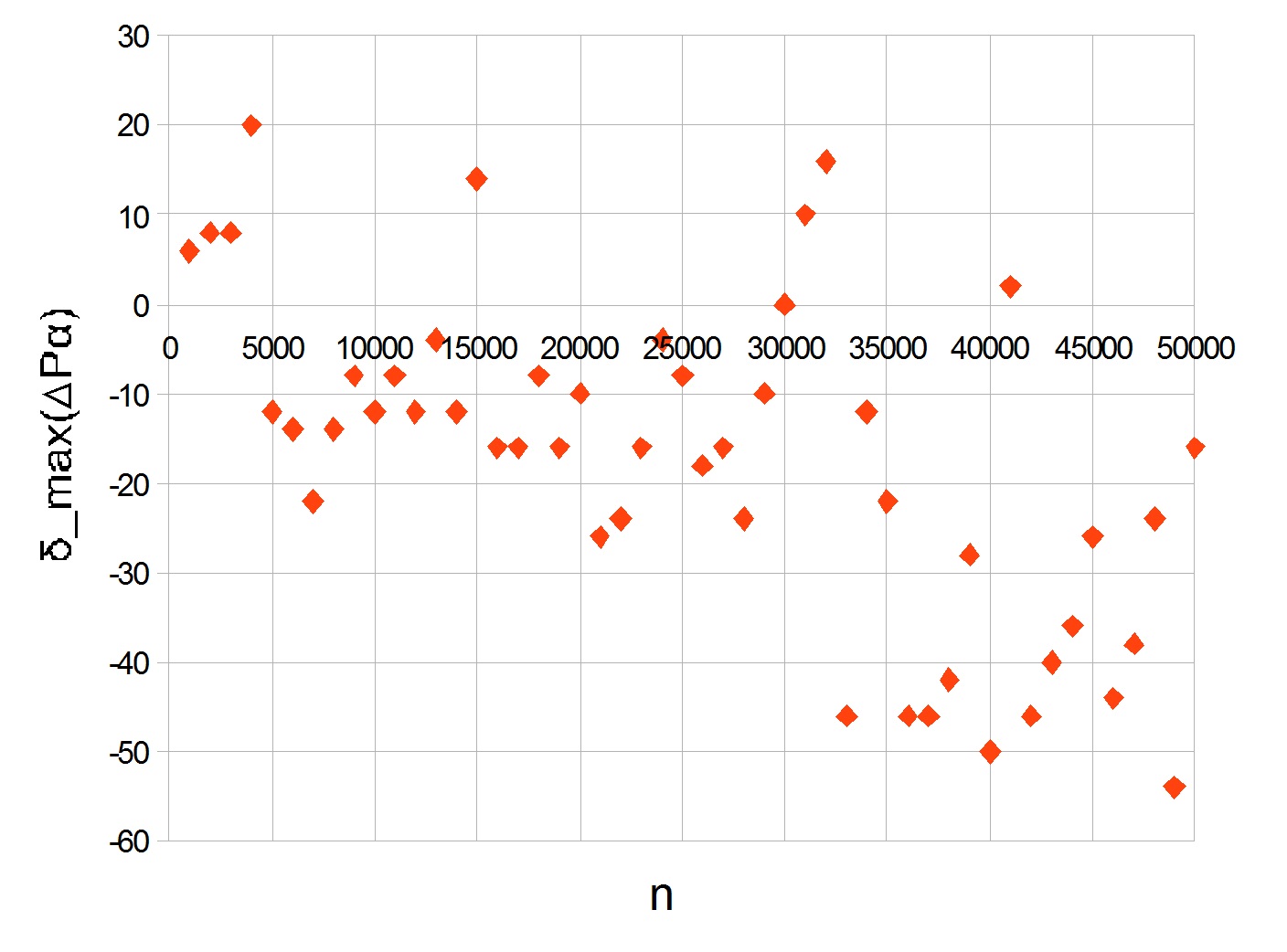
峰值在20处可见。随着n的增加，曲线变为负数，表明大素数的增长率降低。

第二个考虑是优化素数序列的计算。
上式中列出的算法是枚举除数的改进方法。 改进之处是排除偶数，仅检查小于平方的素数的可除性。 候选号码的根。 该算法最困难的部分是对其余mod函数集的计算。 通过优化此功能可以降低复杂度。 但是，还有一种更有效的方法。 让 $$$（r_ {j + 1} ^ {n-1}）= {r_ {2}，r_ {3}，... r _ {\ pi（\ sqrt {P_ {n-1}}）}}$ 是从最后找到的质数除以3到质数根的质数的残基序列。 我们将形成以下形式的序列

$$

$$（r_ {i，j + 1} ^ {n}）= {（r_ {2} + 2i）\，mod \，P_2，（r_ {3} + 2i）\，mod \，P_3，... \\（r _ {\ pi（\ sqrt {P_ {n-1}}）} + 2i）\，mod \，P _ {\ pi（\ sqrt {P_ {n-1}}）}}，（P_ {n -1} + 2i）\，mod \，P _ {\ pi（\ sqrt {P_ {n-1} + 2i}）}}$$

从开始 $$$i = 1$ 。 如果满足以下条件，则计算最后一项 $$$\ pi（\ sqrt {P_ {n-1} + 2i}）\ neq \ pi（\ sqrt {P_ {n-1}}）$ 。 在计算的某些步骤时，余数 $$$r_ {i，j + 1} ^ {n}$ 等于0，转到下一个序列。 一直进行到找到所有残数都不为零的i为止。 这意味着找到下一个质数。 顺序 $$$（r_ {j + 1} ^ {n}）$ 必须保存它，直到找到下一个素数。 用于以这种方式计算素数的递归公式转换为：

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt {0} ^ {i}}（\ mathbf {Dt {0} ^ {j}}（r_ {i，j + 1} ^ { n}）），\ \ \ \ forall \，n \ geqslant 3$$

在提出的算法中，简化了操作mod ： $$$（r_ {j + 1} + 2i）/ P_ {j + 1}$ 倍数的分隔线。 唯一的例外是新的简单分隔符的出现。 在计算机内存中，实现算法时，有必要将素数数组存储到所求根，以及可变残差数组。 一般意义上的算法复杂度（工作量）可能小于其他已知方法。 其中最复杂的操作是平方根的提取，残差的计算和乘法。 根可以提取到最接近的整数。 要获得残差，您可以使用基于可除性一般规则的有效算法。 乘法仅使用2个相对较小的数字i 。 通过根据i的值分配工作，可以减少算法的时间复杂度。 以这种方式获得的分段筛在多线程计算机上应该可以更快地工作。 但是，由于股息增加，所执行的工作将更大。 您也可以将车轮分解分解“拧入”算法。 使用轮毂的最佳尺寸，可以在n的特定范围内降低复杂度-直到硬件“狂野”降低了速度。

也许有人会派上用场。