上一部分（关于线性回归，梯度下降及其全部工作原理）
-habr.com/zh/post/471458在本文中，我将首先展示针对分类问题的解决方案，正如他们所说的那样，“ pens”，而没有用于SGD，LogLoss和计算梯度的第三方库，然后使用PyTorch库。
目的：对于描述泛黄和对称性的两个分类特征，确定对象所属的类别（苹果或梨）（通过模型对对象进行分类）。
首先，上传我们的数据集：
import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10)
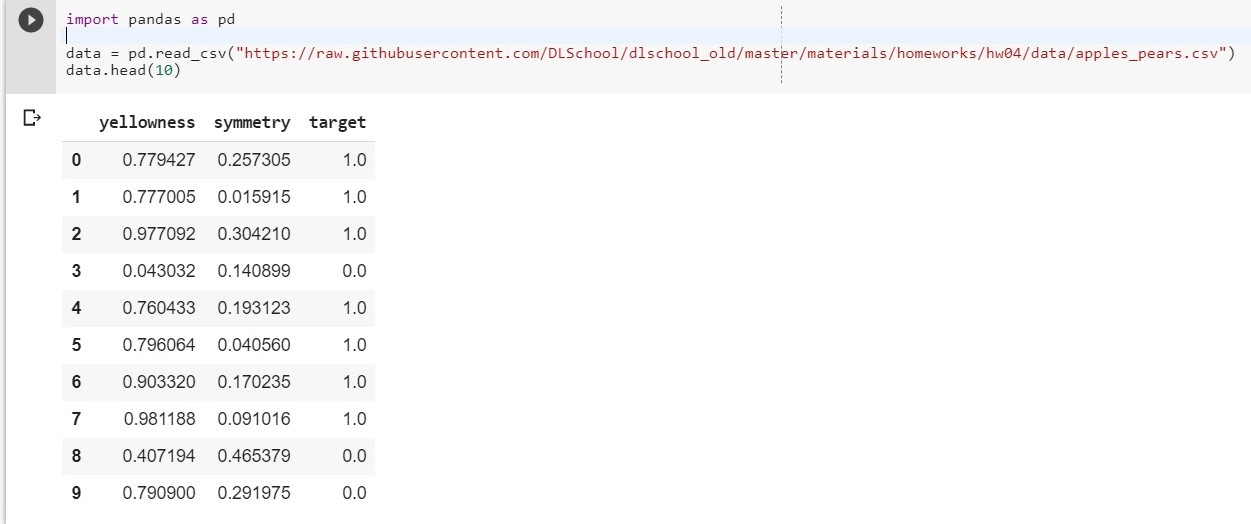
令：x1-黄度，x2-对称度，y =靶
我们组成函数y = w1 * x1 + w2 * x2 + w0
（w0将被视为偏差（英语-偏差））
现在我们的任务简化为找到权重w1，w2和w0，它们最准确地描述了y对x1和x2的依赖性。
我们使用对数损失函数：
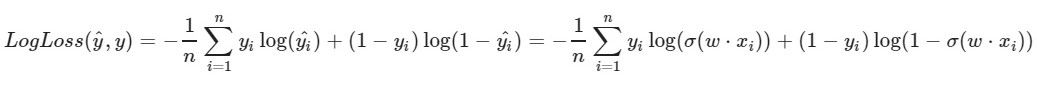
函数的左侧参数是当前权重w1，w2，w0的预测
该函数的正确参数是正确的值（类为0或1）
σ（x）是x的S形
激活函数log（x）-x的自然对数
显然，损失函数的值越小，我们选择的权重w1，w2，w0就越好。 为此，请选择
随机梯度下降 。
我注意到LogLoss的公式会有所不同，因为以下事实：在SGD中，我们选择一个元素而不是整个选择（或子样本，如小批量梯度下降的情况）：
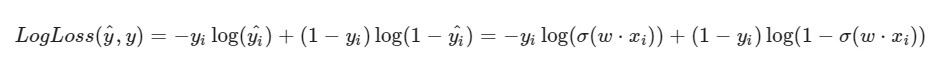解决方案进度：初始权重w1，w2，w0被赋予随机值
我们取数据集的第i个对象（例如，随机数），为其计算LogLoss（使用我们最初分配随机值的w1，w2和w0），然后为权重w1，w2和w0中的每一个计算偏导数，然后更新每个权重。
一些准备： import pandas as pd import numpy as np X = data.iloc[:,:2].values
实现方式： import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1) print(w1, w2, w0)
[0.49671415] [-0.1382643] [0.64768854]
[0.87991625] [-1.14098372] [0.22355905]
* _grad是相应权重的导数。 我将写出通用公式：
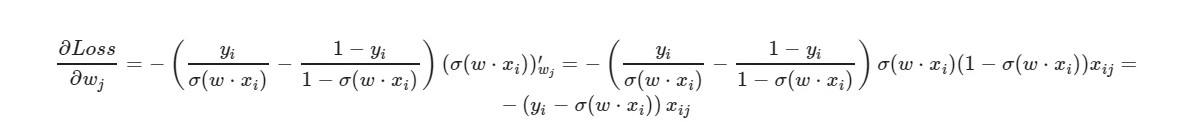
对于自由项w0-因子x被忽略（取等于1）。
使用导数的最终公式，我们可以看到我们不需要显式计算损失函数（我们只需要偏导数）。
让我们检查一下训练集中的对象有多少，我们的模型给出了正确的答案，还有多少-错误的答案。
i = 0 correct = 0 incorrect = 0 for item in y: if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item): correct += 1 else: incorrect += 1 i = i + 1 print(correct, incorrect)
925 75
np.around（x）-舍入x的值。 对于我们：如果x> 0.5，则值为1。如果x≤0.5，则值为0。
如果对象的特征数为5，我们将怎么办？ 10个？ 100？ 并且我们将有适当数量的权重（偏倚加一）。 显然，手动处理每个砝码并为其计算梯度是不方便的。
我们将使用流行的PyTorch库。
PyTorch = NumPy +
CUDA + Autograd（自动计算梯度）
PyTorch实施：
import torch import numpy as np from torch.nn import Linear, Sigmoid def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step X = torch.FloatTensor(data.iloc[:,:2].values) y = torch.FloatTensor(data['target'].values.reshape((-1, 1))) from torch import optim, nn neuron = torch.nn.Sequential( Linear(2, out_features=1), Sigmoid() ) print(neuron.state_dict()) lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer) for epoch in range(n_epochs): loss = train_step(X, y) print(neuron.state_dict()) print(loss)
OrderedDict（[['0.weight'，张量（[[-0.4148，-0.5838]]）），（'0.bias'，张量（[0.5448]]]））
OrderedDict（[['0.weight'，张量（[[[[5.4915，-8.2156]]）），（'0.bias'，张量（[-1.1130]]]））
0.03930133953690529
测试样品的损失相当不错。
在此，选择
MSELoss作为损耗函数。
有关线性的更多信息简而言之：我们给输入2个参数（如上例中的x1和x2），给输出一个参数（y），然后将其馈送到激活函数的输入。 然后就已经计算出它们：误差函数的值，梯度。 最后，权重将更新。
文章中使用的材料