您想了解的有关倒摆的所有信息

对于那些想使自己的倒立摆的人来说，本文可以作为备忘单。 这是我经过多次修改后所遇到的问题，需要对理论进行简要的概述以了解如何稳定系统。

我为什么需要这个？

简而言之：我想扩展CNC机床，但是出了点问题...

尝试失败

该项目花了将近两年的反复试验，重新设计，等待细节和不完整的假期，所以那些希望重复的人节省了时间和精力，我认为有必要谈论不成功的决定。

• 陀螺仪（MPU6050）而不是编码器-基本上没有陀螺仪，但是传感器应该位于旋转的杆上，这会带来不可预测的效果，并且无法使杆绕轴滚动数次。
  
• 绝对编码器-如果是电位计，即使电线的移动（主要是由于arduino中的接触）也会在测量中引入噪声，但10位ADC仍然不够； 如果它是更昂贵的传感器，则通过串行接口进行读取，这会导致系统延迟，尤其是与步进电机结合使用时。
  
• 系统的刚性-在某个时候，我拿了一根铝管，末端带有负载，当车架振动时，其中开始产生强烈的振动，现在还不清楚我们要稳定哪个系统。 我们必须努力确保物理系统尽可能地接近模型。
  
• 摩擦-这种现象通常被忽略，与带小球的滑块的导轨相比，我尝试使用大的滑车轮和V型槽轮廓来减少这种现象，因为 滚动摩擦与半径成反比。
  
• 步进电机的使用-我花了很多时间试图走这条路线，简化公式（实际上，我们立即控制摆锤的加速度）和简化设计（如果我们假设电机不会跳过步距，我们会忘记导轨，电机编码器中的摩擦力）会产生误导。 ，但是...为了准确地控制速度，步骤之间的时间应为数十微秒，这意味着您可以忽略输出到控制台的状态。 没有反馈，您将无法确定电机没有错过任何步骤，并且速度确实是系统所考虑的。 我并不是说这是一个死胡同的解决方案，如果有人成功地使用步进电机来稳定摆锤，那么我将很高兴看到它。
  

自由摆

为了使图片更完整，我们在无摩擦的自由托架上模拟了摆锤。

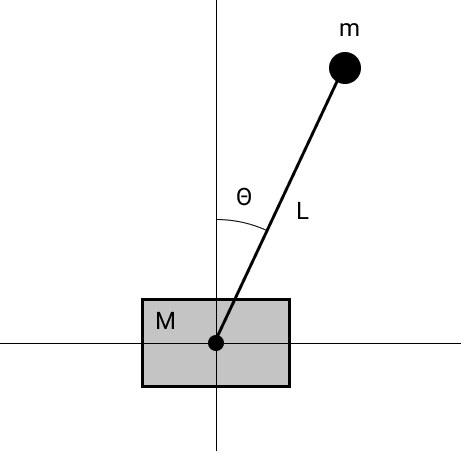
可以通过相对于广义坐标微分拉格朗日来获得运动方程。 我们得到以下方程式：

$$

$$\ begin {cases} L \ cdot \ ddot \ theta + g \ cdot {sin（\ theta）}-\ ddot {x} \ cdot {cos（th）} = 0 \\（m + M）\ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos（\ theta）}-m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin（\ theta ）} = 0 \结束{cases}$$

从中可以找到状态向量的变化方式：

$$

$$\ begin {cases} \ dot \ theta = w \\ \ dot {w} = \ frac {g \ cdot {sin（\ theta）} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin（\ theta）} \ cdot {cos（\ theta）}} {L \ cdot（1 + b \ cdot {cos ^ 2（\ theta））}} \\ \点{x} = v \\ \点{v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {sin（\ theta）}-g \ cdot {sin（\ theta）} \ cdot {cos（\ theta）}} {1 + b \ cdot {cos ^ 2（\ theta）}} \ end {cases}，b = \ frac {m} {M + m}$$

并模拟系统。 代码在这里 。

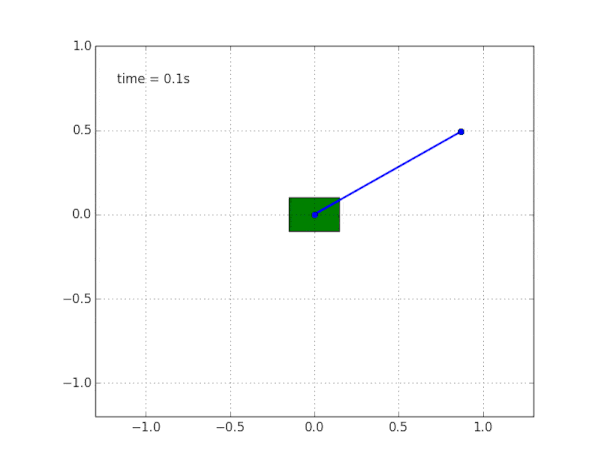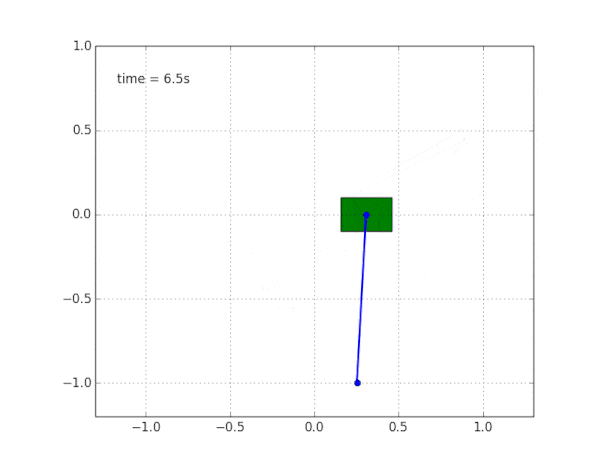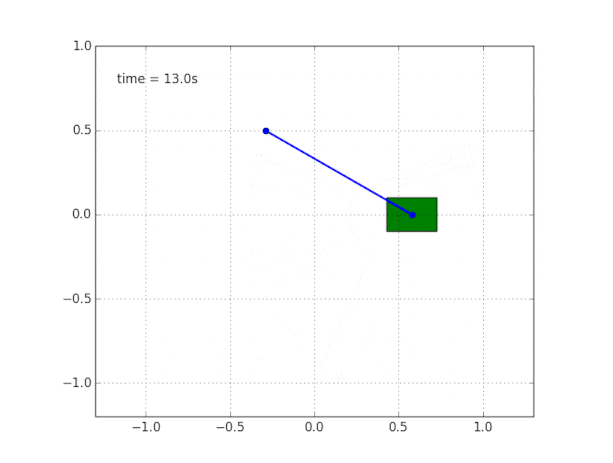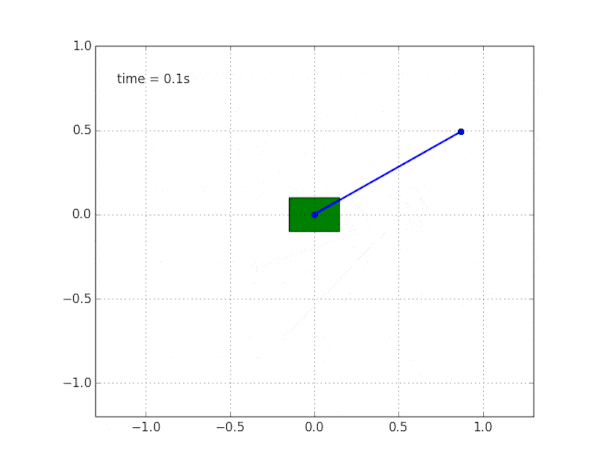
为什么系统不稳定？

常识和可视化告诉我们，摆锤本身将无法承受。 但是如何在数学上进行验证？
一般而言，线性化系统和解决方案如下：

$$

$$\ dot {\ mathbf {x}} = A \ mathbf {x}，\ mathbf {x}（t）= e ^ {At} \ mathbf {x}（0）$$

矩阵幂的指数看起来更清晰，如果我们从特征向量转到坐标系，则矩阵 $$将是对角线（ $$$D$ ），参展商将如下所示：

$$

$$e ^ {Dt} = \开始{bmatrix} e ^ {\ lambda_1t}＆0＆\点＆0 \\ 0＆e ^ {\ lambda_2t}＆\点＆0 \\ \ vdots＆\ vdots＆\ ddots ＆\ vdots \\ 0＆0＆\点＆e ^ {\ lambda_nt} \\ \结尾{bmatrix}$$

现在可以看到，在存在特征值的情况下（ $$$\ lambda_i$ ）的正实部，状态向量的相应分量将趋于无穷大，并且系统将崩溃。 以上内容适用于连续系统， 本视频讲座将介绍有关可持续性的更多信息。
检查是否存在倒立摆的情况。 我们在平衡位置附近线性化系统 $$$\ theta = 0，sin（\ theta）\大约\ theta，cos（\ theta）\大约1，w ^ 2 \大约0$ ：

$$

$$\开始{bmatrix} \点\ theta \\ \点\Ω\\ \点{x} \\ \点{v} \结束{bmatrix} = \开始{bmatrix} 0＆1＆0＆0 \\ \ frac {g} {L（1 + b）} {\ theta}＆0＆0＆0 \\ 0＆0＆0＆1 \\ -g \ frac {b} {1 + b} \ theta＆0 ＆0＆0 \结束{bmatrix} \开始{bmatrix} \ theta \\ \ omega \\ x \\ v \结束{bmatrix}$$

非零特征值的形式为 $$$\ pm \ sqrt {\ frac {g} {L（1 + b）}}$ ，因此我们确信不稳定。

添加反馈

现在，力量将作用在马车上 $$$f$ ，等式之一可以用以下形式重写： $$$（m + M）\ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos（\ theta）}-m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin（\ theta）} = f$ ，线性化系统将采用以下形式：

$$

$$\开始{bmatrix} \点\ theta \\ \点\Ω\\ \点{x} \\ \点{v} \结束{bmatrix} = \开始{bmatrix} 0＆1＆0＆0 \\ \ frac {g} {L（1 + b）} {\ theta}＆0＆0＆0 \\ 0＆0＆0＆1 \\ -g \ frac {b} {1 + b} \ theta＆0 ＆0＆0 \结束{bmatrix} \开始{bmatrix} \ theta \\ \ omega \\ x \\ v \结束{bmatrix} + \开始{bmatrix} 0 \\ \ frac {1} {L} \ frac {1} {2m + M} \\ 0 \\ \ frac {1} {2m + M} \ end {bmatrix} \ cdot {f}$$

现在系统（ $$$\点{\ mathbf {x}} = A \ mathbf {x} + Bu$ ）变得可控 ，这可以通过检查矩阵的等级来验证 $$$\开始{bmatrix} B && AB && A ^ 2B && A ^ 3B \结束{bmatrix}$ 等于状态向量的维数，即 4.为了使摆锤保持直立位置，我使用了线性二次状态控制器，即 控制（u或f）是状态向量的乘积 $$$[\ theta，\点{\ theta}，x，\点{x}]$ 通过最小化二次函数的参数向量来实现。 仿真代码在这里 。

引擎控制

现在您需要控制直流电动机，它包含许多我不知道的参数，因此我将其用作“黑匣子”，由以下等式描述，并考虑了摩擦：

$$

$$\开始{cases} \ dot {x} = v \\ \ dot {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {sign（v）} \ end {cases}$$

您可以在此处阅读有关方程式推导和参数估计的信息 。 下面，我给出了带电压的电动机的加速度曲线图，该曲线图取决于电压（实际上，PWM信号是从控制器输出的）和拟合曲线。

我还通过蛮力代码找到了模型系数。
因此，控制器为我们提供了所需的加速度，并且从第二个方程式中，已知所有常数，即可找到电压。

将真实设备放在一起

现在，我们拥有收集和稳定摆锤的所有知识。 我使用以下铁：

• Arduino Mega 2560不是UNO，因为两个编码器需要4个引脚进行中断
• 摆锤编码器-OMRON E6B2-CWZ6C每转2500个脉冲-给我们一个角度，我们计算角速度，分辨率很高，因此有足够的有限差而无需平滑和平均
• 电机编码器-LPD3806-600BM-G5-24C每转600脉冲-给出滑架的位置，计算速度
• 带5：1变速箱的12V直流电动机
• 10Amp 5V-30V电机驱动器

因此，我们显式地测量摆的角度，滑架的位置，计算摆的角速度和滑架的速度-我们获得了完整的状态，我使用此脚本找到了控制器参数。 出乎意料的是，一切都很快恢复了原样。 我对结果感到满意，它站立甚至可以盛放一杯！


Arduino的代码在这里
与youtube上的许多选项相比，可以改进的地方-这种摆锤很安静，因为PWM在听觉范围之外进行了调谐，并使用了塑料轮。
现在，这项任务看起来像是一项实验室工作：测量电动机的参数并找到调节器的系数，同时了解正在发生的事情。

接下来是什么？

我打算制作一个摆锤：摆一个秋千，摆脱一圈电线，用方便的连接器制作一个屏蔽罩，这样一来捐赠给某些学校或博物馆就不会感到羞耻。 如果有人想加入，我将很高兴有更多雄心勃勃的想法。

参考文献

• 反摆问题的详细描述
• 我们咀嚼一个线性二次调节器来控制倒立摆 -本文为我节省了很多时间来建立我的摆
• 伟大的TAU视频讲座

感谢您的关注！