与节省地铁的规则相反，为了节省时间，我们每个人在自动扶梯中至少跑了一次。 乍一看，这似乎是绝对合乎逻辑的和正确的：如果您想更快地离开-尝试尽早进入平台。 但是，几乎立即想到以下情况：您直下自动扶梯，下到平台，车门正好在您的鼻子前关闭。 当您等待下一班火车时-与您有时间站在一起的同时在自动扶梯上站起来的人们安静地走下车，乘坐下一班火车。 在这种情况下，没有收益。 那么，使自动扶梯滑落到底有多合理？值得这样做吗？ 我赶紧取悦你-找到答案了！ 下面是数学上的理由，证明了在地铁的自动扶梯上行驶时的不便之处（是的，不是）。
任务说明
在进行数学推理之前，值得一提的是，自然地，我根本不是第一个考虑这个问题的人。 在互联网上，您可以找到足够多的文章，甚至是有关该主题的联邦渠道的新闻报道。 然而，每次这样的实验的实质在于通常在自动扶梯上运行，随后将获得的时间与人站在自动扶梯上的时间进行比较。 如果作者试图评估下坡的效果，则略好。 如果他们仍然提供统计信息，那就更好了。 顺便说一下，对于统计，我要特别感谢您。 由于这些实验不够清晰，缺乏实用的结论，我构想并随后对正在进行的过程进行了分析。
因此，我们制定问题的条件并表示限制：
- 实验（心理）涉及两个人，他们两个人在随机的时间同时接近自动扶梯，却不知道火车在哪里。
- 其中一个人站在自动扶梯上，花时间下降。
等于自动扶梯的移动时间。 - 第二个使自动扶梯加速，从而提高了自动扶梯的速度
次，从而将下降时间减少了相同的次数： 
。 - 有效地被认为是这种加速下降，导致以下事实：站在自动扶梯上的人没有时间上火车，其中逃离自动扶梯的人有时间上车。
- 表示为
-有效下降的可能性。 然后，根据纳什均衡法，只有在有效下降的可能性大于或等于无效下降或停止就位的可能性（即0.5）时，一个人才愿意冒险并跑下自动扶梯。 如果有效下降的可能性大于或等于0.5，则将自动扶梯降下来的决定称为“ 适当” 。 如果小于0.5- 不切实际 。 - 我们忽略了这样一个事实：在现实生活中，通常在离开自动扶梯后或要等人们离开汽车后，必须与汽车保持更远的距离，火车以可变的间隔行进并且在开门和关门后保持静止，也就是说，我们假设如果火车在离开自动扶梯时正站在车站上，那么其门是打开的，并且实验参与者会立即停在车内，火车本身会打开（关闭）门，并（从车站）立即到达（离开）车站，并且 dnomomentno。
决策进度
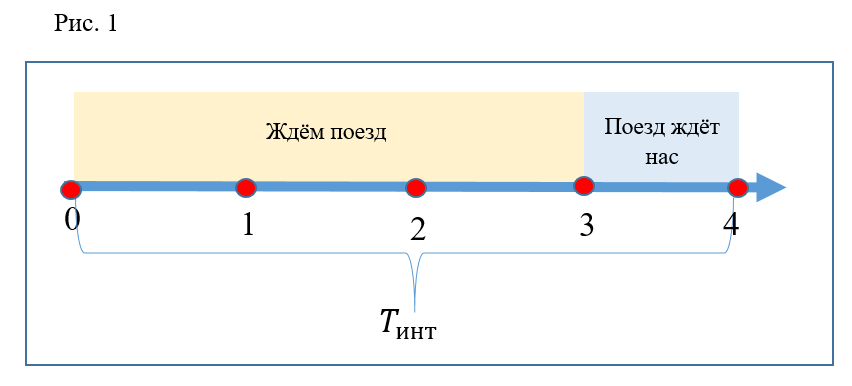
让我们绘制时间轴（图1）。 整个轴将是火车之间的连续间隔。 在下文中，将仅考虑一个间隔。 将显示的间隔分为4个相等的段。 该轴上的点0对应于火车离开车站的时刻。 点3对应于火车的到来和门的打开。 第4点-关闭车门并离开火车。 因此，为了便于图形表示和计算，在火车离开车站的时刻之间计算火车之间的间隔。 前3个时间段是乘客被迫等待到达的火车的时间。 第四部分是火车的停车时间，乘客可以登车。 也把那个时间
（在自动扶梯上下降的时间）等于两个航段。 系数
等于2，即下降时间减少2倍且等于一个航段。
现在，确定概率
，找出慢跑的决定将导致下降有效的事实。 例如，如果我们的参与者在时间0接近自动扶梯，那么第一个将在时间上出现在平台上
（图2），以及第二个更早的时刻
。 但是，从图中可以看出，在所有这些时刻，车站都没有火车，这意味着低速行驶效率低下。
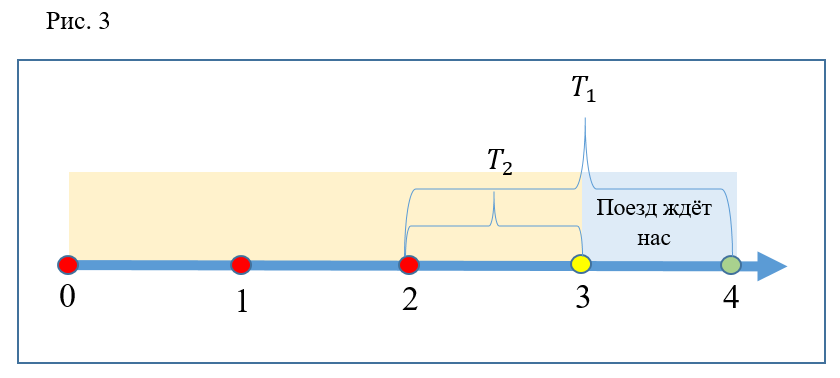
考虑另一种情况（图3）：实验的参与者在时间2到达自动扶梯。和前面的情况一样，第一个在时间出现在平台上
，目前第二个更早
。 但是很明显，这两次火车都在车站。 因此，两个人都将有时间登上同一列火车，因此，撞车效率低下。
此外，容易理解的是，在从2到3的间隔中的任何时间，向下行驶都是有效的，因为逃生的人总是设法登上火车，而不是逃生的人。 如果您在3到4之间选择时间点，那么两个参与者都将晚点上火车，并被迫一起等待下一个，即再次行驶是无效的。
事实证明，在4个传统时间段中，只有参与者在2到3次之间接近自动扶梯时才有效运行（图4）。 进入它的概率为1/4。 因此，在给定的任务条件下，决定下车是不切实际的，因为第二个参与者更有可能（以3/4的概率）徒劳地奔跑，并将被迫与第一个参与者一起等待火车，后者随后又下降了。
以下言论将是完全公平的：
- 火车之间的间隔可以减少也可以增加。 停车时间可能会增加，等待时间可能会减少（以相同的间隔），反之亦然。
- 自动扶梯下降的速度是恒定的，但下降时间可能会有所不同，因为车站的深度或多或少。
- 第二个参与者的跑步速度可能不会比自动扶梯快2倍，而是3倍甚至4倍。
为了评估上述因素变化的影响，有必要推导这些值与有效下降时登上自动扶梯的概率之间的关系。
为此，我们将描述另一种情况（图5）。 我们保留所有原始数据不变，但以下一项除外：系数
增加到4。也就是说，第二个参与者的底部比第一个参与者快4倍。 为方便起见，我们将间隔分为8个相等的部分。 因此，自动扶梯的下降时间现在等于4段，火车在2处停止，等待时间为6，下降时间单独运行。 不难发现，现在“有效”时间间隔（从4到7个时间点）的长度为3。即，概率
等于3/8。 这已经比第一种情况更多，但是我们根本没有进行这些更改来评估可能性。
根据图4和图5，很明显，“有效”段的长度为
。 将其除以间隔的长度即可得出概率
在哪里
。
我们执行一系列转换：
。
最终公式：
。
基于此公式，可以立即得出几个基本结论：
- 如果总间隔不变，则概率值不受停车时间和火车等待时间的变化影响（图6）。
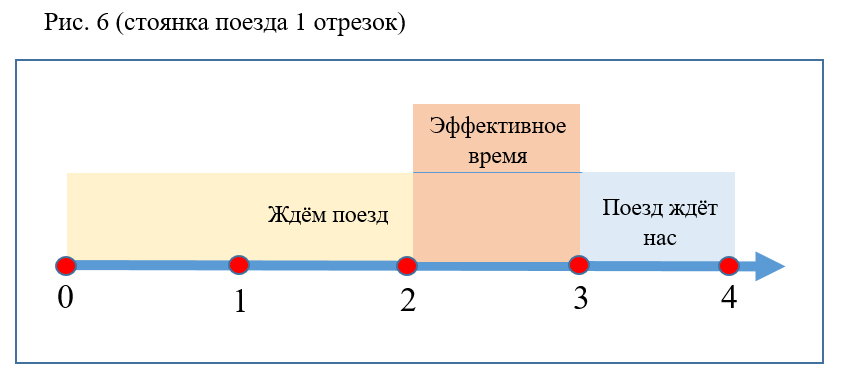
- 火车之间的间隔越大，概率P越低（图7）。
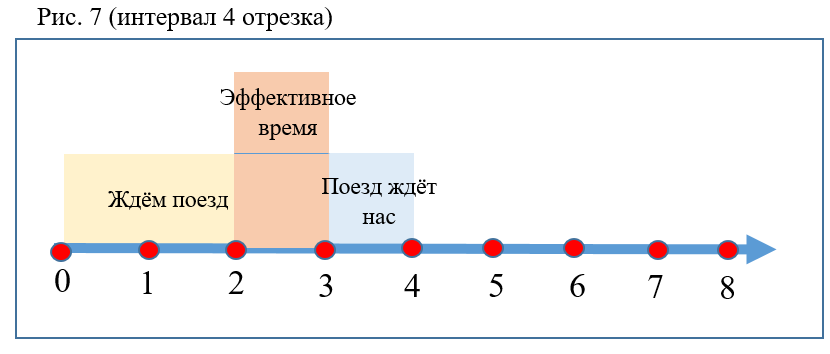
- 如果自动扶梯下降时间与间隔和/或系数K的比率增加，则概率增加。
保真度检查
现在，让我们看看派生公式的正确性如何？
为了验证公式的正确性，我们转向统计数据，该数据在2014年由The Village记者提供。 我表示我的认可，自然，在文章结尾，我将留下原始文章的链接。 统计信息也可以以可视信息图表的形式显示。
实验1.地铁站Chekhovskaya
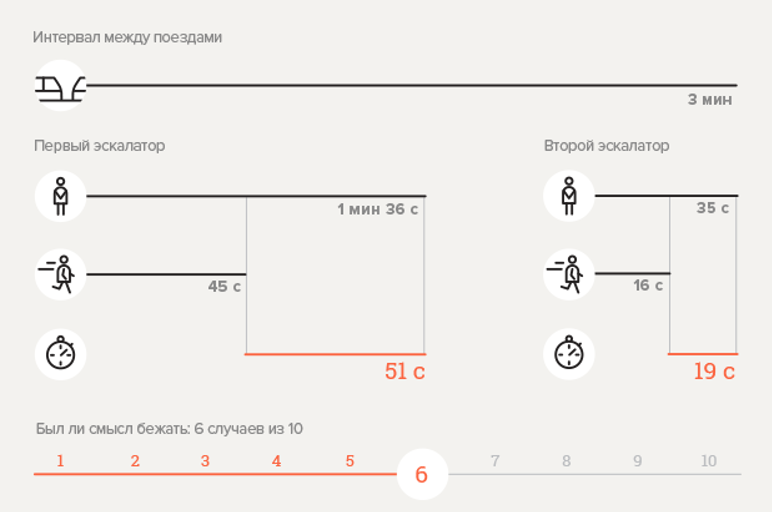
计算概率
。
在这里
;
;
;
;
。
显然，获得的结果与实验数据不同。 公式错了吗？ 不行 从图表中可以看出，下降到车站涉及到两个自动扶梯的行程，但是，没有考虑它们之间的过渡时间。 如果出于可靠性考虑，我们假设过渡过程至少需要30秒，则替换一个新值
我们得到：
;
，更接近实验结果。 还值得注意的是，该实验仅提供了10次重复。 通过增加重复次数，可以使计算出的数据与实验期间获得的结果几乎完全重合。
实验2.地铁站“胜利公园”
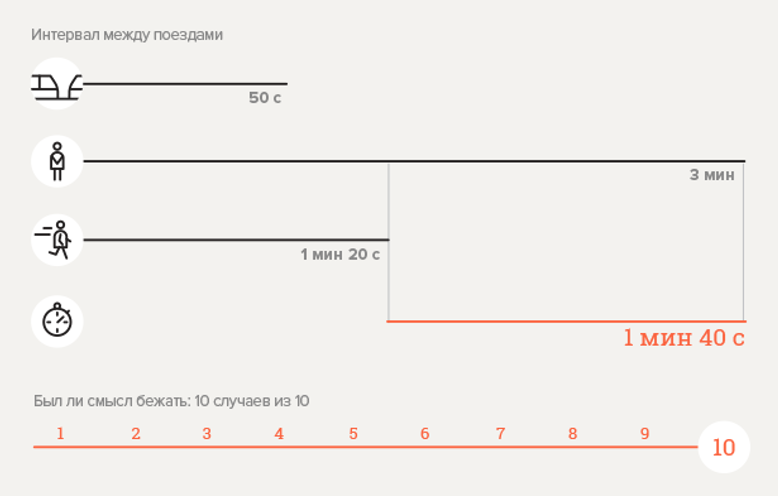
计算概率
。
在这里
;
;
;
;
。
可以看出，我们得到的概率大于1。 但是这里没有矛盾。 如果看一下公式的一般形式，显而易见的是，在自动扶梯的下降时间等于列车之间的间隔的情况下，速度增加至少2倍将使加速下降有效的概率等于0.5。 如果自动扶梯的行进时间大于间隔时间，则系数相同
早点乘火车的可能性只会增加。 最后，如果自动扶梯的下降时间是间隔的2倍或更多倍，则在100％的情况下，行人将及时乘火车，而其余的自动扶梯将没有时间。 我们在本实验中观察到的就是这种效果：通讯员得出结论，在10例病例中有10例被冲走。
实验3. Park Kultury地铁站
计算概率
。
在这里
;
;
;
;
。
又是一个错误？ 一点也不。 可以看出，如上所述，自动扶梯的下降时间是列车间隔的2倍。 运行时间减少了2倍。 事实证明，每一次下降都应该是有效的。 但是请不要忘记，在开始讨论之前，我们对门的瞬时关闭以及至少火车从车站的瞬时离开进行了假设。 如果您想像图8中所示的选项，那么很明显，在现实生活中，一个失控的人可能没有时间坐在第一点（例如，火车将早些离开），而在第二点，火车将延迟一点时间，然后一个非奔跑的人会和一个在前一趟火车上奔跑的迟来的人一起坐在里面。
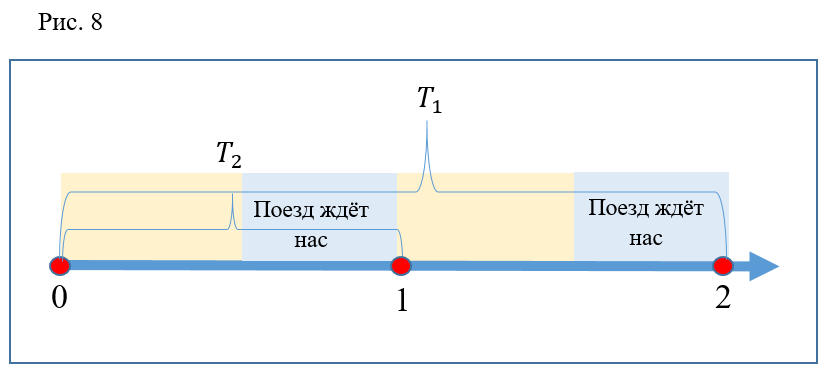
我想这是在两个“无效”时期发生的。 有充分的理由争辩说，随着实验重复次数的增加，“有效”运行的百分比将趋于100％。
结论
现在，根据可用的实验数据，可以确定公式的正确性，我们将对其进行分析并得出结论。 因为从一开始我们就同意，如果有效下降的可能性大于或等于0.5，我们将考虑权宜之计。 就是说，从字面上看，如果我们可以确定至少有一半的情况是有充分理由可以运行的，那确实值得冒险冒险运行，因为如果我们迟到了，我们几乎将一无所获。 基于上述内容，我们将概率公式重写为：
。
有趣的是，正如我们已经发现的，始终在
。 同时，如果
，无论您跑多快，早点上火车的可能性都小于0.5，因为很明显，
永远不会大于或等于1。
现在让我们看一下通讯的速度。 平均而言，它约为自动扶梯速度的2倍（下降时间减少2倍）。 通常，这些数据与我自己的实验结果吻合（我看不出要点）。 通常，要以至少3的K系数发展速度已经很困难了。有很多人想要在真正的自动扶梯上楼下奔跑，而且，站在他们左边的人或他们的东西（包，手提箱）可能会干扰。 均值
和
。 也就是说，只有在比率达到
不小于1。并且只有当自动扶梯下降的下降时间不小于列车之间的间隔时，才有可能。 在真正的地铁中，火车之间的平均间隔为2分钟，因此并非所有车站都可以拥有很长的下降时间。 通常，即使在圣彼得堡地铁中，自动扶梯的行进时间约为1分钟30秒，即比该间隔短0.75倍。 由此得出一个非常明显且最重要的基本结论：如果您确定该站的自动扶梯的移动幅度小于火车之间的间隔，那么沿它运行是不切实际的。
附言：请注意以下事实：该任务没有考虑到乘坐特定运输工具的需要。 这完全是关于登上平台然后登上火车。
实验数据来源：
The Village 。 再次感谢！