以分类问题为例的机器学习中的惯性思想（SGDm），缩放思想（Adagrad）和正则化思想

此后使用的数据集来自此处已经通过的kaggle竞赛。
在数据选项卡上，您可以阅读所有字段的描述。

所有源代码都在此处为笔记本电脑格式。

我们加载数据，检查我们通常具有：

import numpy as np import pandas as pd dataset = pd.read_csv('../input/ghouls-goblins-and-ghosts-boo/train.csv') #   X_test = pd.read_csv('../input/ghouls-goblins-and-ghosts-boo/test.csv') #   print(dataset.shape) print(dataset[:10]) 

类型字段的值（食尸鬼，鬼魂，地精）仅替换为0、1和2。

颜色-还需要进行预处理（我们只需要数字值即可构建模型）。 我们将为此使用LabelEncoder和OneHotEncoder。 更多细节 。

 from sklearn.preprocessing import LabelEncoder, OneHotEncoder labelencoder_X_1 = LabelEncoder() X_train[:, 4] = labelencoder_X_1.fit_transform(X_train[:, 4]) labelencoder_X_2 = LabelEncoder() X_test[:, 4] = labelencoder_X_2.fit_transform(X_test[:, 4]) labelencoder_Y_2 = LabelEncoder() Y_train = labelencoder_Y_2.fit_transform(Y_train) one_hot_encoder = OneHotEncoder(categorical_features = [4]) X_train = one_hot_encoder.fit_transform(X_train).toarray() X_test = one_hot_encoder.fit_transform(X_test).toarray() 

好了，现在我们的数据已经准备好了。 仍然需要训练我们的模型。

首先申请Adagrad ：

从本质上讲，这是对随机梯度下降的修改，我上次写的内容是： habr.com/en/post/472300

该方法考虑了每个单独参数的所有过去梯度的历史（缩放的想法）。 这使您可以减小具有较大梯度的参数的学习步长：



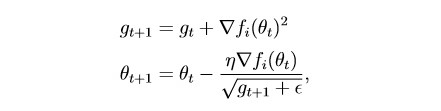
g是缩放参数（g0 = 0）
θ-参数（重量）
epsilon是为了防止被零除而引入的一个小常数

将数据集分为两部分：
培训样本（培训）和验证（验证）：

 from sklearn.model_selection import train_test_split x_train, x_val, y_train, y_val = train_test_split(X_train, Y_train, test_size = 0.2) 

为模型训练做些准备：

 import torch import numpy as np device = 'cuda' if torch.cuda.is_available() else 'cpu' def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step 

自我训练模式：

 from torch import optim, nn model = torch.nn.Sequential( nn.Linear(10, 270), nn.ReLU(), nn.Linear(270, 3)) lr = 0.01 n_epochs = 500 loss_fn = torch.nn.CrossEntropyLoss() optimizer = optim.Adagrad(model.parameters(), lr=lr) train_step = make_train_step(model, loss_fn, optimizer) from sklearn.utils import shuffle for epoch in range(n_epochs): x_train, y_train = shuffle(x_train, y_train) #    X = torch.FloatTensor(x_train) y = torch.LongTensor(y_train) loss = train_step(X, y) print(loss) 

型号等级：

 #  : test_var = torch.FloatTensor(x_val) with torch.no_grad(): result = model(test_var) values, labels = torch.max(result, 1) num_right = np.sum(labels.data.numpy() == y_val) print(' {:.2f}'.format(num_right / len(y_val))) 

在这里，除了图层外，我们只有2个可配置的参数（目前）：
学习率和n_epochs（时代数）。

根据我们如何结合这两个参数，可能会出现3种情况：

1-一切都很好，即 该模型显示出训练样本的损失低而验证样本的准确性高。

2-拟合不足-训练样本损失较大，而验证样本的准确性较低。

3-过度拟合-训练样本损失小，但验证样本准确性低。

首先，一切都很清楚:)

在第二个方面，似乎也要尝试学习率和n_epochs。

并与第三怎么办？ 答案很简单-正则化！

以前，我们有以下形式的损失函数：
L = MSE（Y，y），无需附加条款
正则化的本质恰恰在于，在目标函数中添加一项，如果梯度太大，则“优化”梯度。 换句话说，我们对目标函数施加了限制。

有很多正则化方法。 有关L1和L2的更多信息-正则化： craftappmobile.com/l1-vs-l2-regularization /＃_ L1_L2

Adagrad方法实现L2正则化，让我们应用它吧！

首先，为清楚起见，我们查看未进行正则化的模型指标：

lr = 0.01，n_epochs = 500：
损失= 0.44 ...
准确度：0.71

lr = 0.01，n_epochs = 1000：
损失= 0.41 ...
准确度：0.75

lr = 0.01，n_epochs = 2000：
损失= 0.39 ...
准确度：0.75

lr = 0.01，n_epochs = 3000：
损失= 0.367 ...
准确度：0.76

lr = 0.01，n_epochs = 4000：
损失= 0.355 ...
准确度：0.72

lr = 0.01，n_epochs = 10000：
损失= 0.285 ...
准确度：0.69

在这里，您可以看到4k +时代-该模型已经过拟合。 现在让我们尝试避免这种情况：

为此，请为我们的优化方法添加weight_decay参数：

 optimizer = optim.Adagrad(model.parameters(), lr=lr, weight_decay = 0.001) 

当lr = 0.01时，m_epochs = 10000：
损失= 0.367 ...
准确度：0.73

在4000年代：
损失= 0.389 ...
准确度：0.75

事实证明要好得多，但是我们在优化器中仅添加了1个参数：)

现在考虑SGDm（这是一个随机梯度下降，具有很小的扩展范围-启发式，如果您愿意）。

最重要的是， SGD在每次迭代后都会非常强烈地更新参数。 使用过去迭代的梯度（惯性思想）“平滑”梯度是合乎逻辑的：



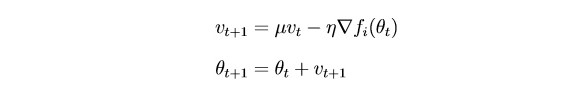
θ-参数（重量）
µ-惯性超参数

没有动量参数的SGD：



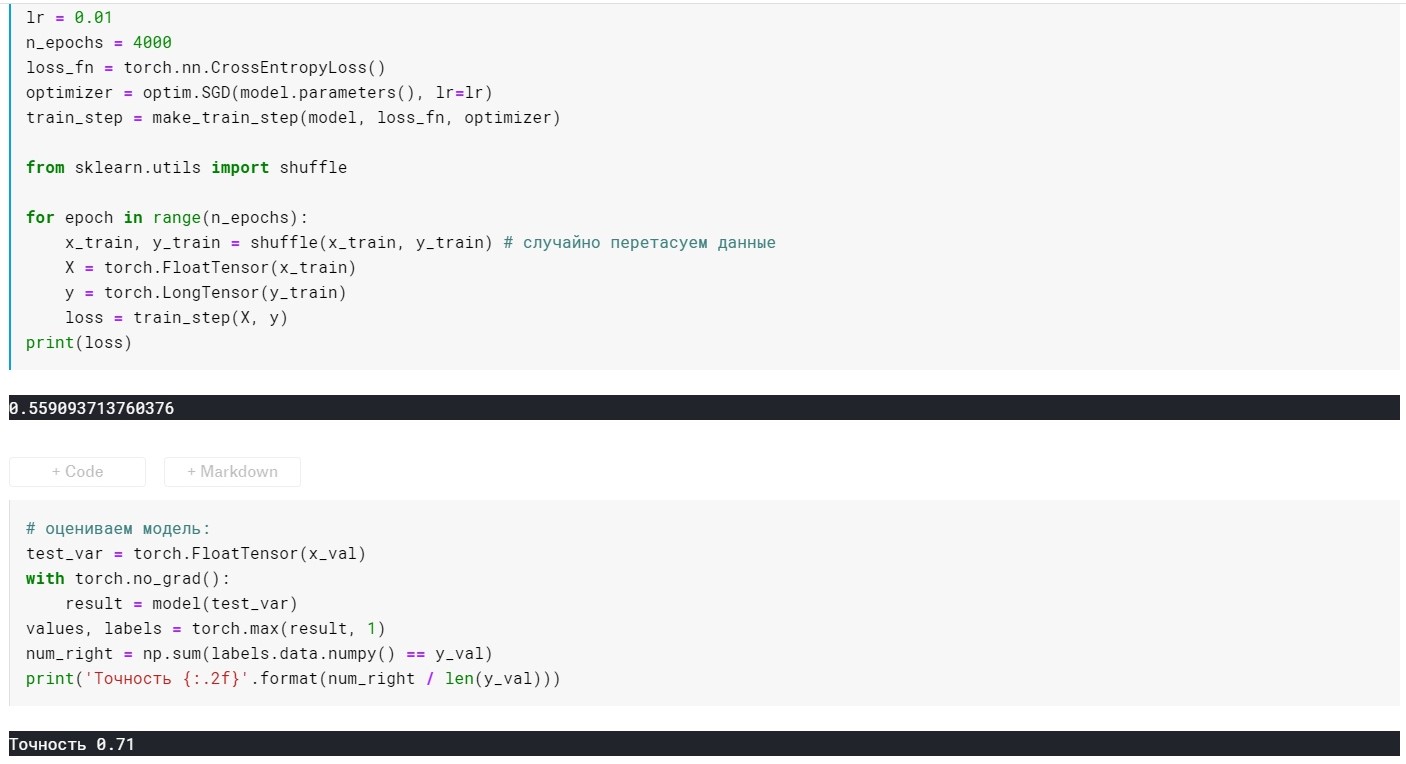
具有动量参数的SGD：



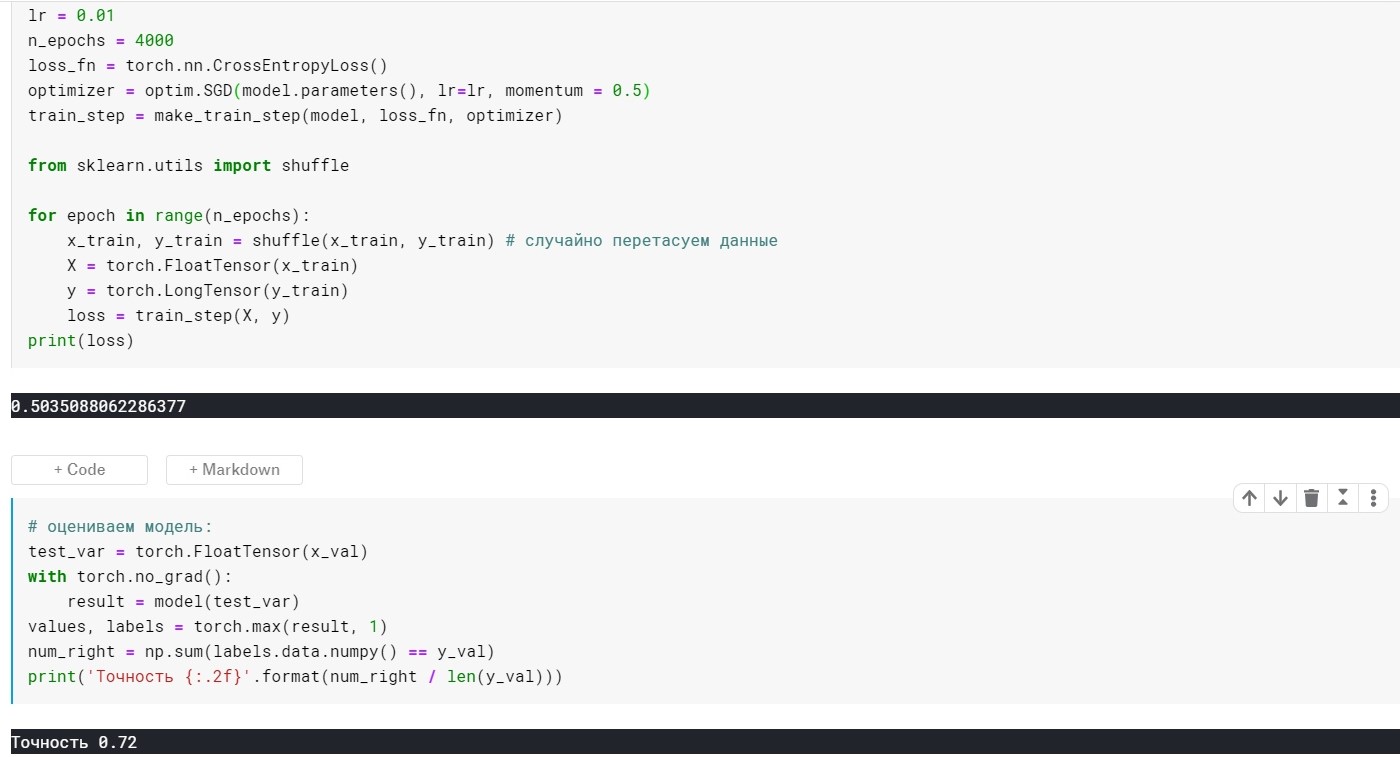
事实证明并没有好多少，但是这里的要点是，有些方法可以立即使用缩放和惯性的思想。 例如，Adam或Adadelta，现在显示出良好的效果。 好了，为了理解这些方法，我认为有必要了解一些简单方法中使用的一些基本思想。

谢谢大家的关注！