本文的翻译是为基础和高级课程“数据科学的数学”中的学生特别准备的。
贝叶斯定理是统计学和概率论中最著名的定理之一。 即使您不从事计算定量指标的工作，您也可能在某个时候必须熟悉该定理才能为考试做准备。
P（A | B）= P（B | A）* P（A）/ P（B）看起来就是这样，但这意味着什么，又如何工作？ 今天，我们将找出并深入了解贝叶斯定理。
确认我们的判断的理由
概率论和统计学的重点是什么？ 最重要的用途之一涉及不确定性下的决策。 当您决定执行任何操作时（当然，除非您是一个有理智的人），您敢打赌，在完成此操作之后，与未执行此操作相比，它将带来更好的结果……但是投注是一回事不可靠，您最终将如何决定采取此步骤还是不采取此步骤？
一种或另一种方式是评估成功结果的概率，如果该概率高于某个阈值，则应采取措施。
因此，准确评估成功可能性的能力对于做出正确的决定至关重要。 尽管随机性将始终在最终结果中发挥作用，但您仍应学习正确使用这些随机性，并随着时间的推移将它们转化为您的优势。
这就是贝叶斯定理生效的地方-它为我们提供了量化的基础，以保持我们对随着环境因素变化而采取的行动的结果的信念，这反过来又使我们能够随着时间的推移改进决策过程。
让我们分析一下公式
让我们再次看一下公式：
P（A | B）= P（B | A）* P（A）/ P（B）在这里：
- P（A | B） -事件A发生的可能性，前提是事件B已经发生；
- P（B | A） -事件B发生的概率，前提是事件A已经发生。 现在看起来像是一个恶性循环，但是我们很快就会了解该公式为何有效；
- P（A） -事件A发生的先验（无条件）概率；
- P（B） -事件B发生的先验（无条件）概率。
P（A | B）是后验（条件）概率的一个示例，即，后验概率用于测量周围世界某个状态（即事件B发生的状态）的概率。 而P（A）是先验概率的示例，可以在周围世界的任何状态下进行测量。
让我们以示例的方式来看一下贝叶斯定理。 假设您最近从Bootcamp完成了数据分析课程。 您还没有收到接受您采访的一些公司的答复，并开始担心。 因此，您要计算特定公司向您提供工作机会的可能性，前提是已经过去了三天并且他们没有给您回电话。
我们根据示例重写公式。 在这种情况下，结果A（
要约 ）正在收到工作邀请，而结果B（
要约 ）是“三天没有打来电话”。 基于此，我们的公式可以重写为：
P（ 报价 | NoCall ）= P（ 报价 | NoCall ）* P（ 报价 ）/ P（ NoCall ）P（ Offer | NoCall ）的值是接收报价的概率，前提是三天内没有通话。 这种可能性极难评估。
但是，倒数概率
P（ NoCall | Offer ） ，也就是连续三天没有打电话，考虑到最终您收到了公司的工作邀请，很有可能会附加一些价值。 通过与朋友，招聘人员和顾问的交谈，您会发现这种可能性很小，但是有时，如果一家公司仍计划邀请您工作，那么它仍然可以保持沉默三天。 因此，您评估：
P（ NoCall | 提供 ）= 40％40％不错，似乎还有希望！ 但是我们还没有完成。 现在我们需要评估上班的可能性
P（ Offer ） 。 每个人都知道找到工作是一个漫长而艰巨的过程，您可能必须多次面试才能获得此优惠，因此您要评估：
P（ 要约 ）= 20％现在我们只需要评估
P（ NoCall ） ，即三天内您不会收到公司打来电话的可能性。 有很多原因可能导致您在三天之内不给您回电话-他们可能拒绝您的候选人资格，或者仍然与其他候选人进行面试，或者招聘人员生病了，因此没有打电话。 嗯，有很多原因导致您可能无法拨打电话，因此您将这种可能性评估为：
P（ NoCall ）= 90％现在，将它们放在一起，我们可以计算
P（ Offer | NoCall ） ：
P（ 优惠 | NoCall ）= 40％* 20％/ 90％= 8.9％这是很小的，因此，不幸的是，为该公司留下希望（并继续将简历发送给其他人）更为合理。 如果仍然有点抽象，请不要担心。 当我第一次了解贝叶斯定理时，我有同样的感觉。 现在，让我们看看我们如何达到这8.9％（请记住，您最初的20％分数已经很低了）。
公式背后的直觉
还记得我们说过贝叶斯定理为我们的判断提供依据吗？ 那么它们来自哪里呢？ 它们取自先验概率
P（A） ，在我们的示例中称为
P（ Offer ） ，实际上，这是我们对一个人获得工作机会的可能性的初步判断。 在我们的示例中，您可以假设先验概率是您离开面试那一刻将获得工作机会的概率。
出现新信息-3天过去了，公司未给您回电。 因此，我们使用等式的其他部分来调整新事件的先验概率。
让我们看一下概率
P（B | A） ，在我们的示例中称为
P（ NoCall | Offer ） 。 当您第一次看到贝叶斯定理时，您会问自己：如何知道从何处获得概率
P（B | A） ？ 如果我不知道
P（A | B）的概率
是多少，那么我应该如何神奇地知道
P（B | A）的概率呢？ 我记得
查尔斯·芒格曾经说过的一句话：
“翻转，总是翻转！”
- 查尔斯·芒格
他的意思是，当您尝试解决一个难题时，您需要将其倒置并从另一个角度看待它。 这正是贝叶斯定理所做的。 让我们根据统计量重新表述贝叶斯定理，以使其更易于理解（我
从这里了解到）：
例如，对我而言，这样的记录看起来更加清晰。 我们有一个先验假设（Hypothesis）-我们得到了一份工作，并且有明显的事实-证据（Evidence）-三天没有打来电话。 现在，我们要考虑提出的事实，以了解我们的假设正确的可能性。 如上所述，我们有概率
P（A）= 20％ 。
是时候颠倒一切了！ 我们使用
P（ 证据 | 假设 ）从另一侧看问题，然后问：“在我们的假设为真的世界中，这些证据事件发生的概率是多少？” 因此，如果我们回到示例中，我们想知道如果他们在三天内不给我们打电话，我们仍然有可能被录用。 在上图中，我将
P（ 证据 | 假设 ）标记为“ scaler”（缩放器），因为该词很好地反映了含义的本质。 当我们将其乘以一个先验值时，它会降低或增加发生事件的概率，具体取决于证明我们的假设是否“有害”的任何事件。 在我们的情况下，不打电话的日子越久，我们被叫上班的可能性就越小。 3天的沉默已经很糟糕（它们使我们的先验概率降低60％），而20天不打电话的情况将完全摧毁找工作的希望。 因此，证据事件累积的越多（没有电话的时间越多），定标器降低可能性的速度越快。 定标器是贝叶斯定理用来调整我们的判断的一种机制。
在本文的原始版本中，我遇到了一件麻烦事。 这就是为什么
P（ 证据 | 假设 ）比P（假设|证据）更容易评估的原因。 其原因是，
P（ 证据 | 假设 ）是关于世界的判断领域非常有限。 缩小范围，我们简化了任务。 我们可以用火和烟进行类比，其中火是我们的假设，对烟的观察是证明有火存在的事件。
P（火|烟）更难评估，因为很多因素都会引起烟-汽车尾气，工厂，用木炭煎炸汉堡包的人。 同时，
P（烟|火）更容易评估，因为在有火的世界中，几乎肯定会有烟。
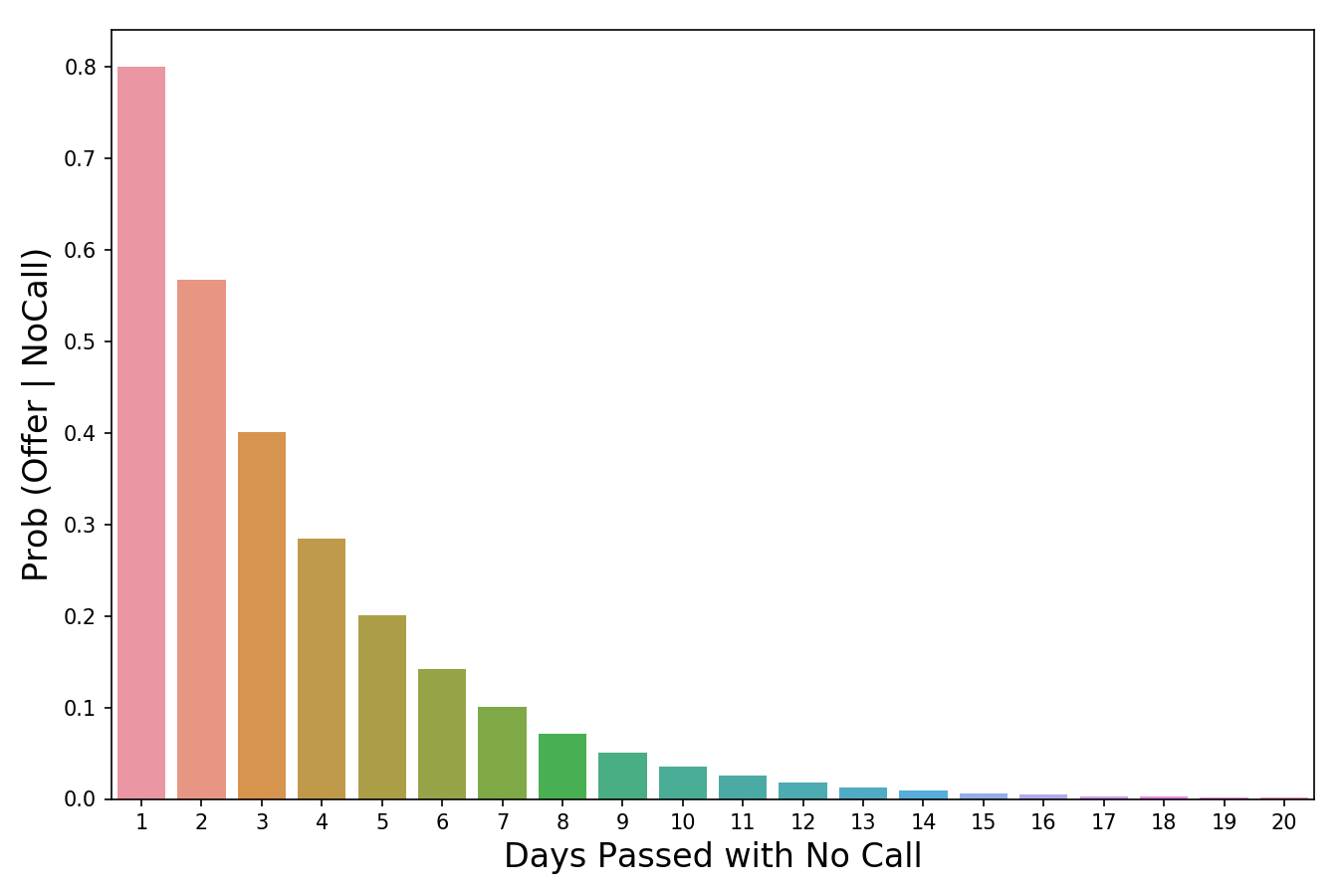概率值随着不打电话的天数而减少。公式的最后一部分
P（B）或
P（ Evidence ）是归一化器。 顾名思义，其目的是标准化先验概率与定标器的乘积。 如果没有规范化器，我们将具有以下表达式：
注意，先验概率与缩放器的乘积等于联合概率。 并且由于其中的
P（ 证据 ）成分之一，因此联合概率将受到事件发生频率的影响。
这是一个问题，因为共享概率是一个包含世界所有状态的值。 但是我们不需要所有状态，我们只需要由事件证据确认的状态即可。 换句话说，我们生活在一个事件众多的世界中-证据已经发生，事件的数量也不再重要（因此，我们不希望它们从原则上影响我们的计算）。 将先验概率与定标器的乘积除以
P（ 证据 ）会将其从联合概率变为有条件（后验）。 条件概率仅考虑发生事件证明的世界上的那些状态，而这正是我们正在实现的状态。
我们可以查看为什么将缩放器划分为规范器的另一种观点是，它们回答了两个重要问题-他们的态度将这些信息结合在一起。 让我们以我最近在
Bayes上的文章为例。 假设我们试图根据单个符号-灵巧性来发现观察到的动物是否是猫。 我们所知道的是，我们所谈论的动物是敏捷的。
- 洁牙机告诉我们，有多少百分比的猫具有敏捷性。 该值应该很高，例如0.90。
- 归一化器告诉我们原则上动物陷阱的百分比。 该值应该是平均值，例如0.50。
- 0.90 / 0.50 = 1.8的比率表示您需要更改先验概率，因为如果您以前不这么认为，是时候改变主意了，因为您最有可能与猫打交道。 可以想到这一点的原因是，我们观察到一些证据表明该动物是敏捷的。 然后，我们发现灵巧猫的比例通常大于灵巧动物的比例。 考虑到目前我们只知道这样的证据，仅此而已，明智的做法是重新考虑我们仍在看猫的思想方向的信念。
总结一下
现在我们知道了如何解释公式的每个部分，我们终于可以将所有内容放在一起，看看发生了什么：
- 面试后，我们立即确定先验概率-我们被录用的机会是20％。
- 没有电话联系的日子越多，我们被录用的可能性就越小。 例如，在三天无人接听电话之后，我们相信在一个可以找到这份工作的世界里，公司只有40％的机会将公司拉得很长，才给您打电话。 将定标器乘以先验概率，得出20％* 40％= 8％
- 最后，我们了解到8％是针对世界可能存在的所有情况计算的。 但是我们只担心三天没有被召集的情况。 为了仅在这些条件下工作，我们将三天之内没有通话的先验概率设为90％，然后得到归一化器。 我们将先前收到的8％除以归一化8％/ 90％= 8.9％，得到最终答案。 总计，在世界所有情况下，如果您在三天内未接到公司的电话，得到工作的可能性仅为8.9％。
希望本文对您有所帮助！