VK有一个具有以下描述的组 ：

每天将同一张照片手动保存到计算机，然后再次上传，逐渐失去质量。

左侧是2012年6月7日上传的原始图片，右侧是现在的图片。

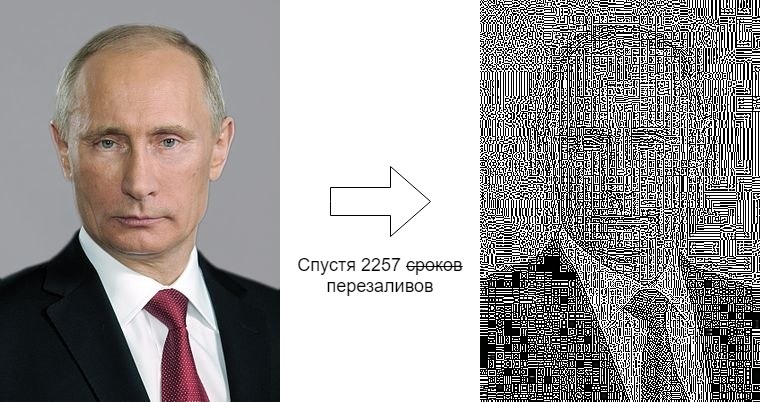
这种差异非常可疑。 让我们尝试弄清楚这7年中发生了什么。 熟识的人在美杜莎（Medusa）上有一篇关于该小组的文章 ，但只有技术方面的人才会引起我们的兴趣。

JPEG为何以及在什么阶段会损失压缩

考虑高度简化的JPEG编码和解码方案。 仅显示那些说明JPEG算法基本原理的操作。

因此，有4种操作：

• DCT是离散余弦变换。
• 量化-将每个值四舍五入到量化步长的最接近倍数：y = [x / h] * h，其中h是步长。
• IDCT是离散离散余弦逆变换。
• 舍入是正常的舍入。 由于这是显而易见的，因此无法在图中显示。 但随后将证明其重要性。

保存所有信息的操作以绿色突出显示（使用浮点数时未考虑丢失），粉红色表示丢失。 即，损耗和伪像的出现不是因为余弦变换，而是因为简单的量化。 本文不会考虑一个重要的阶段-霍夫曼编码，因为它的执行没有损失。

更详细地考虑这些步骤。

DCT

由于DCT有多种变体，以防万一，我将澄清JPEG使用具有归一化功能的第二种DCT 。 编码时，每个图像被分成8x8正方形（每个通道）。 每个这样的正方形可以表示为64维向量。 余弦变换是在另一个正交基础上找到此向量的坐标。 很难可视化64维空间，因此下面将给出2维类比。 您可以想象图片被分为2x1块。 在下面将显示的图形中，x轴对应于块的第一个像素的值，y轴对应于第二个像素的值。

继续使用特定示例进行类比，假设原始图像中两个像素的值分别为3和4。如下图所示，绘制矢量（3，4）。 原始基准以蓝色标记。 向量的坐标在某些新基础上为（4.8，1.4）。

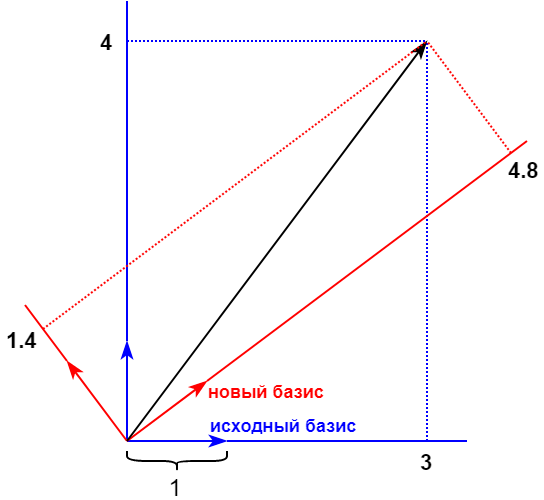
在所考虑的示例中，随机选择了一个新的基础。 DCT提供了非常具体的64维固定基础。 为什么在JPEG中使用它的理由非常有趣，我在另一篇文章中对此进行了描述。 我们将只涉及要点。 通常，所有像素的值均相等。 但是，如果我们使用DCT对其进行转换，则可以在新的基础上从所得的64个坐标（称为DCT变换系数）中安全地将它们中的一些零置零或粗略舍入，而损失最小。 这归功于可压缩图像的功能。

量化

小数值不能保存在文件中。 因此，根据量化步骤，值4.8、1.4将保存如下：

• 在第1步（最温和的选项）：5和1
• 在步骤2：4和2
• 在步骤3：6和0。

通常，每个值的步长选择都不同。 JPEG文件具有至少一个称为量化表的数组，该数组存储64个量化步骤。 该表取决于在任何图形编辑器中设置的压缩质量。

IDCT

与DCT相同，但具有转置基准。 数学上，x = IDCT（DCT（x）），因此，如果没有量化，则可以无损失地恢复。 但是不会有压缩。 由于使用了量化，原始矢量不能总是准确地计算出来。 下图显示了两个示例，这些示例具有准确且不准确的恢复。 倾斜的网格对应于新的基础，直线对应于原始基础。

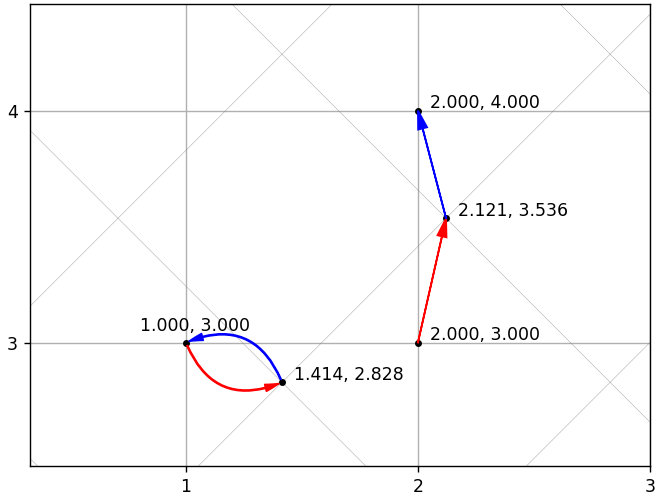
一个明显的问题出现了：转码序列是否可以导致与原始向量有很大不同的向量？ 也许吧

对所有整数向量进行排序并查看它们的代码转换将导致什么会很有趣。 为了减少信息噪声，我们删除了初始网格，然后将各个段直接连接原始向量和重构向量（无中间步骤）。 首先，考虑所有坐标的量化步长等于1。 下图中的新基准旋转了45度，为此，我们得到了不准确回收率的17.1％。 段的颜色没有任何意义，但是对于防止它们的视觉合并很有用。

这个基础是10.3度，而7.4％的不准确回收率：

附近：

而这一比率是6.4％的10.4：

19度（12.5％）：

但是，如果将量化步长设置为大于1，则重构的矢量将开始明显集中在网格节点附近。 这是步骤5：

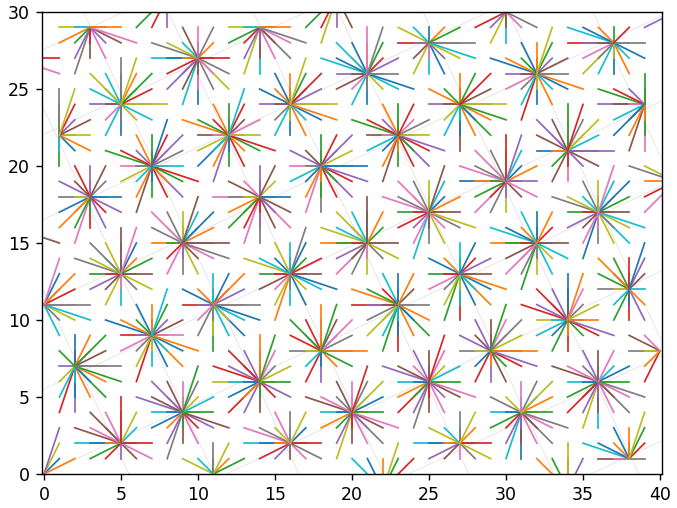
这是2：

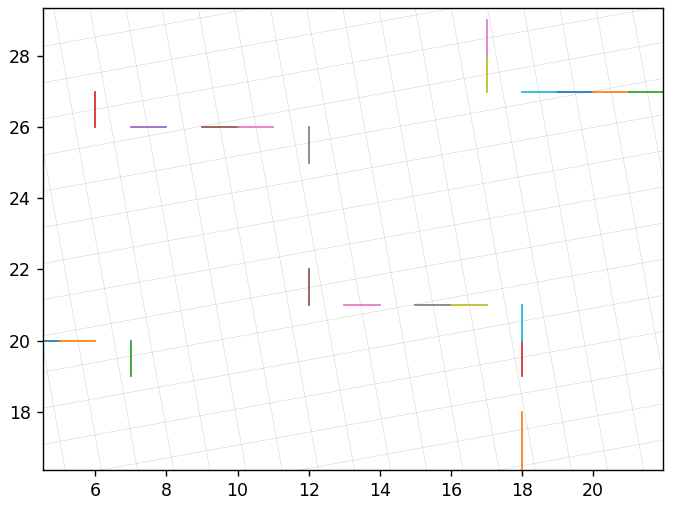
如果以相同的音调对图像进行几次编码，那么与单次编码相比几乎没有任何反应。 这些值似乎“卡”在网格的节点中，不能再从那里“跳转”到其他节点。 如果步长不同，则矢量将从一个网格节点“跳转”到另一个网格节点。 这可以带他去任何地方。 下图显示了具有步骤1、2、3、4的4个代码转换的结果。您可以看到具有步骤12的大网格。该值是1、2、3、4的最小公倍数。

并在此过程中执行-从1到7的步骤。仅显示部分原始向量的可视化效果，以改善可视化效果。

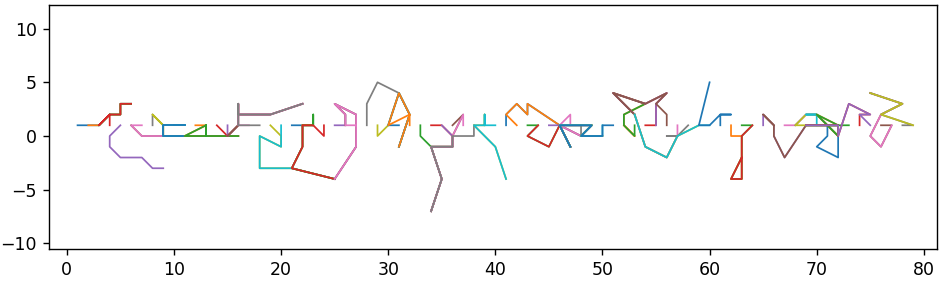
四舍五入

为什么在IDCT之后四舍五入值？ 毕竟，如果您摆脱了这一阶段，那么还原的图像将由小数值表示，并且在重新编码时我们不会丢失任何内容。 从数学的角度来看，我们将简单地从一个基础转到另一个基础，而不会造成损失。 这里有必要提及色彩空间的转换。 尽管JPEG不能调节颜色空间，并且可以直接保存到源RGB中，但是在大多数情况下，使用了初步转换为YCbCr的方法。 眼睛特征等等。 而且这种转换也会导致损失。

假设我们得到了一个压缩质量最高的JPEG文件，也就是说，所有系数的量化步长均为1。 我们不知道使用了哪个编解码器，但是通常在RGB-> YCbCr转换之后，编解码器执行舍入。 由于质量是最高的，因此在IDCT之后，我们得到的分数是小数，但与YCbCr空间中的原始值非常接近。 如果我们四舍五入，那么大多数将被完全恢复。

但是，如果不进行四舍五入，则由于存在如此小的差异，YCbCr-> RGB转换甚至可以将它们与原始值进一步拉开距离。 随着随后的代码转换，差距将越来越大。 为了以某种方式可视化此过程，我们使用主成分方法将64维向量投影到平面上。 然后，对于1000个转码，我们大约得到以下更改序列：

此处的轴绝对值意义不大，但可以使用变形的相对重要性。

多个转码示例

源猫：

重新保存质量为50后：

在具有相同质量的任何后续数量的转码之后，图像均不会改变。 现在，我们将把质量从90逐渐降低到50：1：

下图大约发生了相同的事情：

重新保存质量为20后：

从90到20无缝：

现在有1000次，随机质量从80到90：

10,000次：

VK集团图片分析

让我们开始分析VK集团的2000多张图片。 首先，从最开始检查平均绝对偏差。 x轴是图片编号（或日期），y轴是偏差。

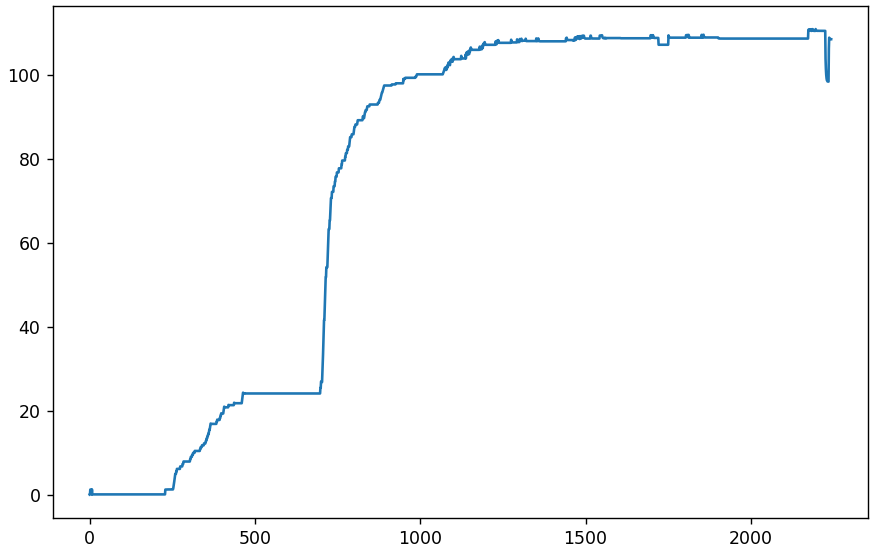
我们继续看显示附近图片的平均绝对偏差的微分图。

一开始的小幅波动是正常现象。 直到232日，一切都进行顺利，图片完全相同。 第233个像素的每个像素突然之间平均相差1.23（从0到255）。 好多 也许量化表刚刚改变。 看看吧。 同时，它与接收到的文件大小相当。

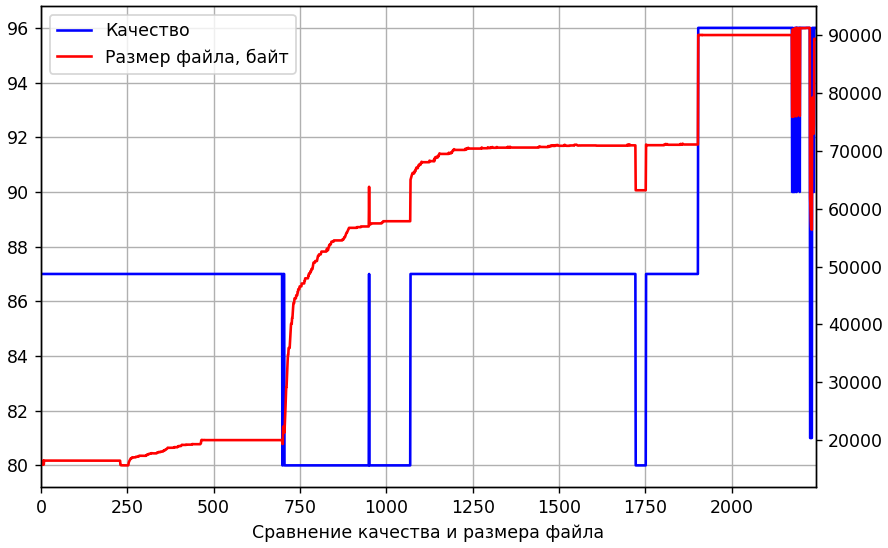
是的，表格已更改。 但不要早于700年代。 然后，也许发生了低质量的中间隐藏转码。 让我们尝试重新编码232nd两次。 第一次，我们将经历不同的质量级别，第二次，我们将使用与从1到700s相同的量化表。 我们的目标是使图片尽可能地类似于233号。 在下图中，沿x轴是中间代码转换的质量，沿y是与第233位的平均绝对偏差。

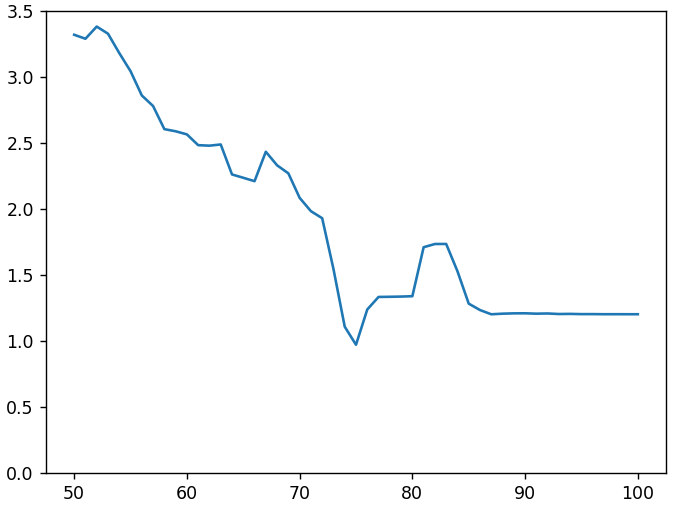
尽管图表上的质量为75％，大约等于1，但它与期望的零仍然相距甚远。 增加第二个中间阶段并更改子采样参数并没有改善这种情况。

对于其余图片，一切都差不多，加上量化表中的变化也被叠加了。 就是说，在某个时候，情况发生了巨大变化，然后在几天之内稳定下来，但是直到出现新的浪潮。 也许服务器上的映像本身发生了变化。 我不能完全排除组管理员的参与。

不幸的是，我没有发现图像真正发生了什么。 至少现在，我确信这不仅仅是重新保存。 但是，最重要的是，更好地表示编码和解码过程中正在进行的过程。 希望你也这样做。

图片存档 ，供独立研究。